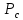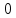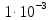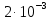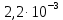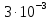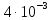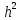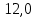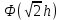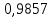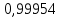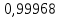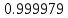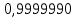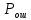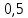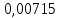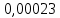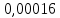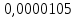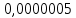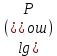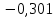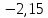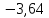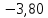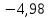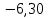Разработка структурной схемы системы связи
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
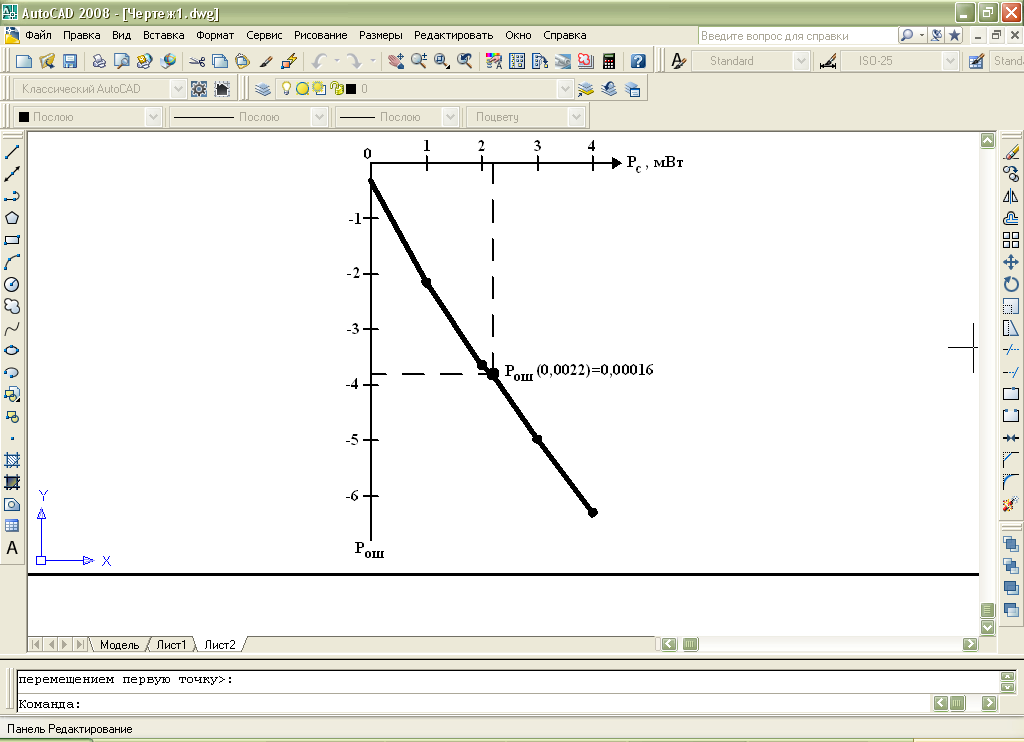
Выбор схемы приемника (демодулятора)ДФМ обеспечивает максимальную помехоустойчивость за счет наибольшего расстояния между сигналами (двоичными). На рис. 2 представлена схема ДФМ приемника когерентного способа приема. 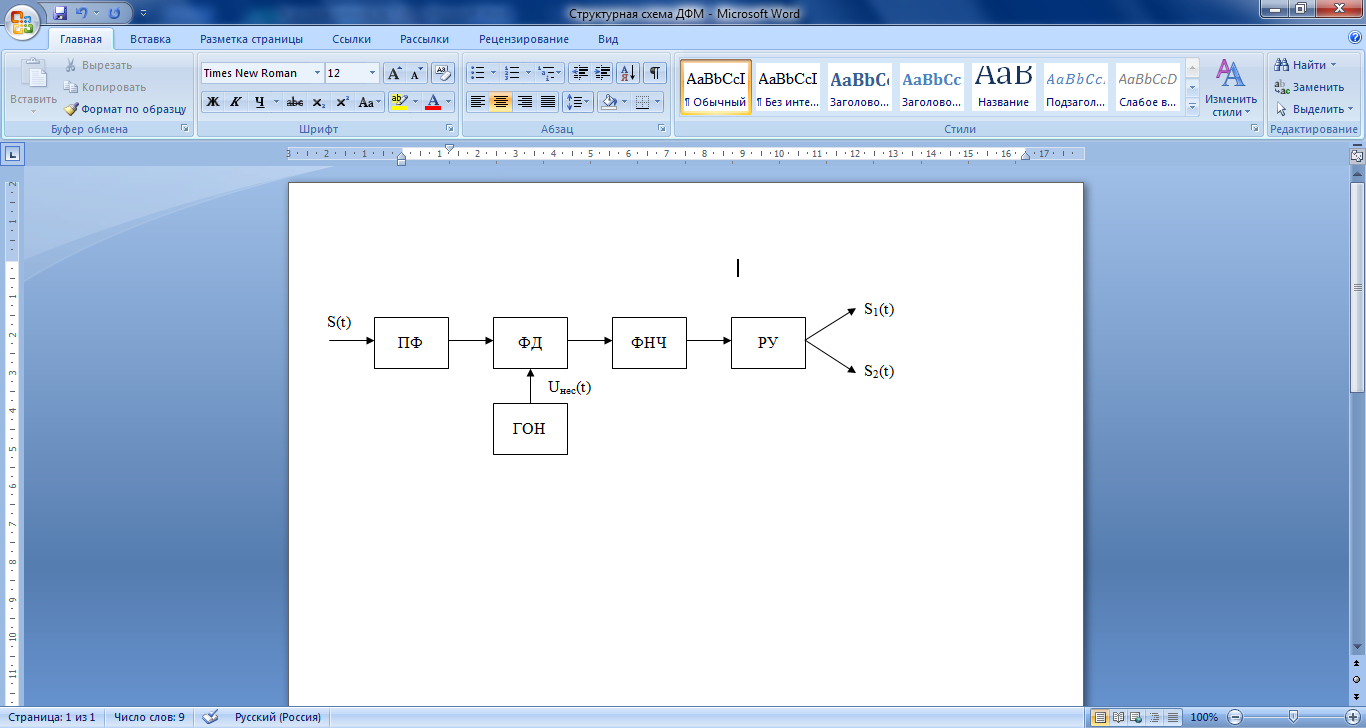 Рисунок 2 Структурная схема ДФМ приемника В данной схеме: Полосовой фильтр (ПФ) предназначен для предварительной фильтрации сигналов, для уменьшения влияния помех, с полосой пропускания 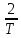 , в присутствии только гауссовских помех не обязателен; , в присутствии только гауссовских помех не обязателен;Фазовый демодулятор выполняет роль корректора, где фазомодулированный сигнал сравнивается по фазе с эталонным сигналом, который обычно называют опорным; Фильтр нижних частот выполняет роль интегратора; Генератор опорного напряжения, частота и фаза колебаний его полностью совпадают с частотой и фазой одного из сигналов; Решающее устройство (РУ) принимает решение о значении выходного сигнала, используя входной сигнал. В случае дискретной фазовой модуляции: 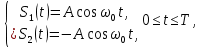 В технике связи широко используются цифровые методы передачи информации. При этом передаваемое сообщение передается последовательностью прямоугольных импульсов. При дискретной модуляции закодированное сообщение 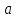 , представляющее собой последовательность кодовых символов, преобразуется в последовательность элементов (посылок) сигнала путем воздействия кодовых символов на переносчик. Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. Обычно в качестве переносчика используют переменный ток (гормоническое колебание). При дискретной фазовой модуляции меняется фаза несущей на , представляющее собой последовательность кодовых символов, преобразуется в последовательность элементов (посылок) сигнала путем воздействия кодовых символов на переносчик. Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. Обычно в качестве переносчика используют переменный ток (гормоническое колебание). При дискретной фазовой модуляции меняется фаза несущей на  при каждом переходе от 1 к 0 и от 0 к 1. при каждом переходе от 1 к 0 и от 0 к 1.На рис. 3 представлена форма сигнала при двоичном коде для ДФМ, где скважность 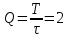 . .Спектры сигналов дискретной модуляции получаются на основе общего правила построения спектров модулированного сигнала по спектру модулирующего НЧ сигнала путем его переноса из «0» на частоту 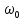 . . Рисунок 3. Временная характеристика дискретной фазовой модуляции Фазомодулированный (ФМ) сигнал имеет постоянную амплитуду, фаза сигнала изменяется пропорционально информационному сигналу, а именно: 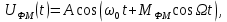 где 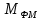 – индекс фазовой модуляции. В данном случае – индекс фазовой модуляции. В данном случае 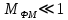 , таким образом данное выражение можно переписать в виде: , таким образом данное выражение можно переписать в виде: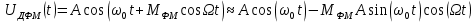 . .Учитывая, что при  . После преобразования получим: . После преобразования получим: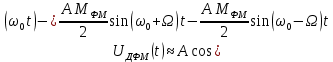 На рис. 4 представлен спектр сигнала ДФМ прямоугольными импульсами со скважностью 2. В ДФМ при 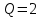 , , 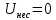 ;при ;при 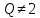 , , 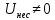 . .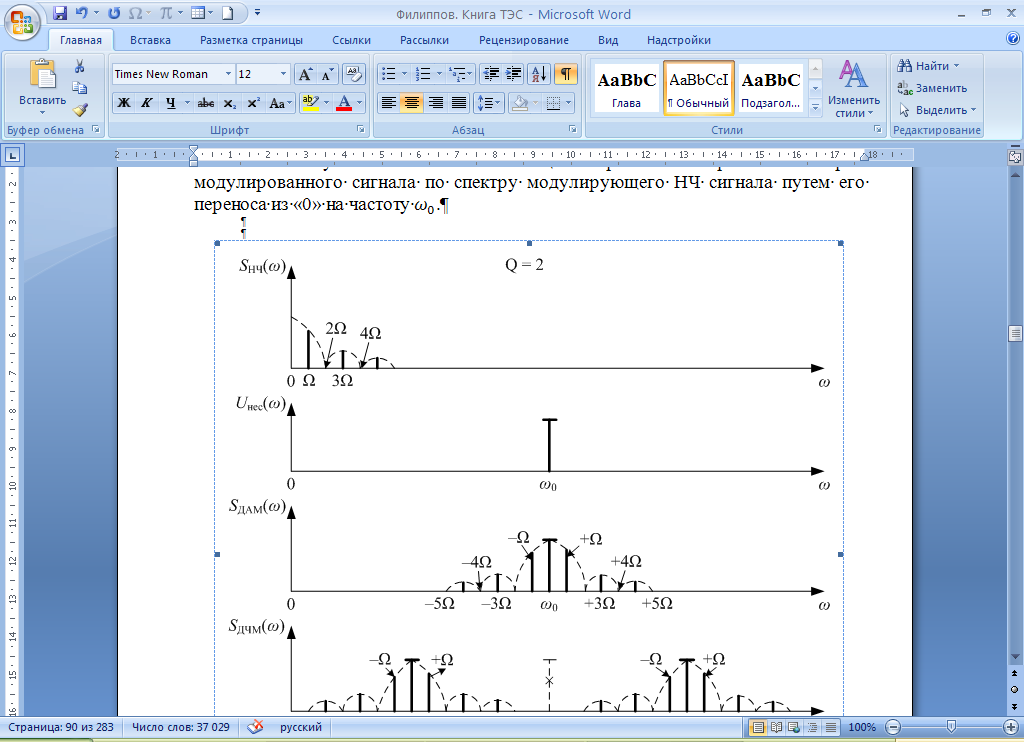 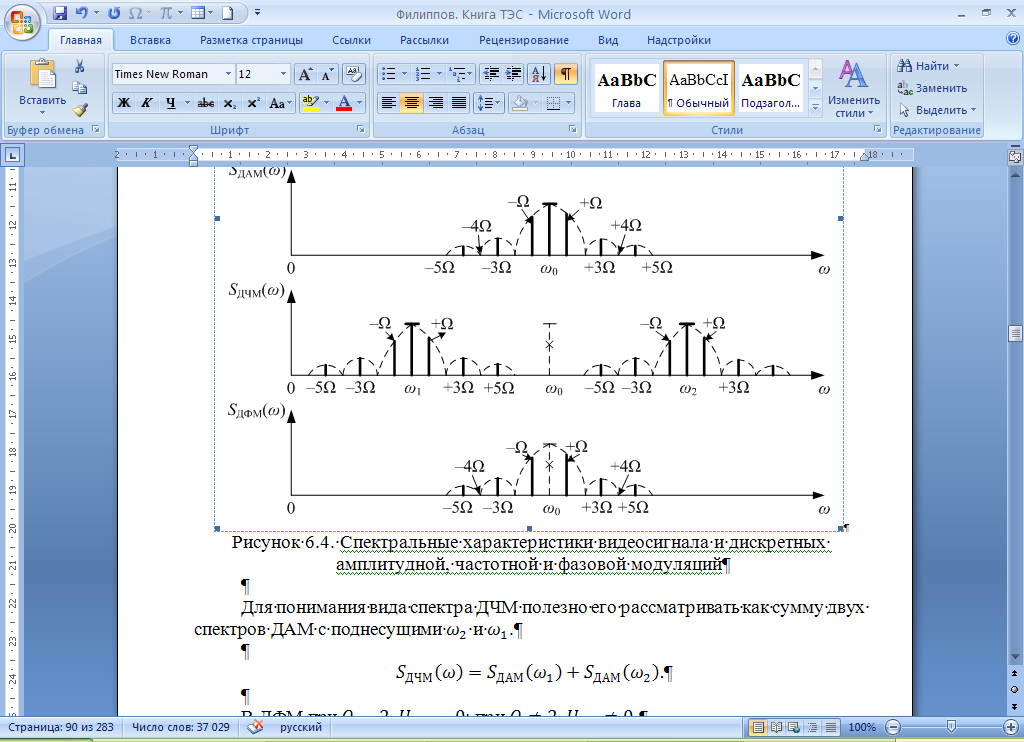 Рисунок 4. Спектральные характеристики видеосигнала и дискретной фазовой модуляции Вероятность ошибки (вероятность искажения элементарной посылки) для ДФМ и когерентного способа приема при флуктуационных помехах типа гауссовского шума определяется следующей формулой: 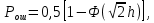 где 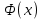 – табулированный интеграл вероятностей (функция Крампа), которая имеет табличное значение; – табулированный интеграл вероятностей (функция Крампа), которая имеет табличное значение;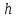 – отношение мощностей сигнала и помехи (отношение сигнал / шум), вычисляемое по формуле: – отношение мощностей сигнала и помехи (отношение сигнал / шум), вычисляемое по формуле: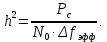 где 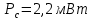 – мощность сигнала на входе демодулятора приемника; – мощность сигнала на входе демодулятора приемника;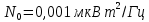 – спектральная плотность мощности помехи; – спектральная плотность мощности помехи;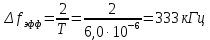 – эффективная полоса пропускания канала связи. – эффективная полоса пропускания канала связи.Произведем численную подстановку: 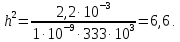 Найдем значение функции Крампа: 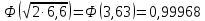 Тогда вероятность ошибки будет: 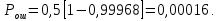 Рассчитаем зависимость вероятности ошибки от мощности сигнала и результаты расчетов сведем в таблицу Таблица 2
График расположен под осью абсцисс в четвертом квадранте. Согласно нему, чем меньше вероятность ошибки, тем ниже на оси ординат располагается соответствующее значение вероятности. На графике указана точка, соответствующая заданной мощности сигнала 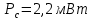 (мощность на входе демодулятора после усиления сигнала высокочастотными усилителями входных цепей приемника). (мощность на входе демодулятора после усиления сигнала высокочастотными усилителями входных цепей приемника). |