Разработка структурной схемы системы связи
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
Помехоустойчивое кодированиеВ реальных условиях приём двоичных символов всегда происходит с ошибками, когда вместо символа "1" принимается символ "0" и наоборот. Ошибки могут возникать из-за помех, действующих в канале связи (особенно помех импульсного характера), изменения за время передачи характеристик канала (например, замирания), снижения уровня передачи, нестабильности амплитудно- и фазочастотных характеристик канала и т.п. Общепринятым критерием оценки качества передачи в дискретных каналах является нормированная на знак или символ допустимая вероятность ошибки для данного вида сообщений. Так, допустимая вероятность ошибки при телеграфной связи может составлять 10-3 (на знак), а при передаче данных – не более 10-6 (на символ). Для обеспечения таких значений вероятностей одного улучшения только качественных показателей канала связи может оказаться недостаточным. Поэтому основной мерой является применение специальных методов повышения качества приёма передаваемой информации. Эти методы можно разбить на две группы. К первой группе относятся методы увеличения помехоустойчивости приёма единичных элементов (символов) дискретной информации, связанные с выбором уровня сигнала, отношения сигнал-помеха (энергетические характеристики), ширины полосы канала, методов приёма и т.д. Ко второй группе относятся методы обнаружения и исправления ошибок, основанные на искусственном введении избыточности в передаваемое сообщение. Увеличить избыточность передаваемого сигнала можно различными способами. Так как объём сигнала 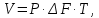 где 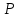 – мощность сигнала, Вт; – мощность сигнала, Вт; 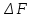 – ширина спектра сигнала, Гц; – ширина спектра сигнала, Гц; 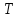 - время передачи сигнала, сек, то его увеличение возможно за счёт увеличения - время передачи сигнала, сек, то его увеличение возможно за счёт увеличения 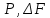 и и 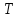 . .Практические возможности увеличения избыточности за счёт мощности и ширины спектра сигнала в системах передачи дискретной информации по стандартным каналам резко ограничены. Поэтому для повышения качества приёма, как правило, идут по пути увеличения времени передачи и используют следующие основные способы: многократная передача кодовых комбинаций (метод повторения); одновременная передача кодовой комбинации по нескольким параллельно работающим каналам; помехоустойчивое (корректирующее) кодирование, т.е. использование кодов, исправляющих ошибки. Иногда применяют комбинации этих способов. Многократное повторение ( 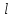 раз) кодовой комбинации является самым простым способом повышения достоверности приёма и легко реализуется, особенно в низкоскоростных системах передачи для каналов с быстро меняющимися параметрами. Способу многократного повторения аналогичен способ передачи одной и той же информации по нескольким параллельным каналам связи. В этом случае необходимо иметь не менее трёх каналов связи (например, с частотным разнесением), несущие частоты которых нужно выбирать таким образом, чтобы ошибки в каналах были независимы. Достоинством таких систем являются надёжность и малое время задержки в получении информации. Основным недостатком многоканальных систем так же, как и систем с повторением, является нерациональное использование избыточности. раз) кодовой комбинации является самым простым способом повышения достоверности приёма и легко реализуется, особенно в низкоскоростных системах передачи для каналов с быстро меняющимися параметрами. Способу многократного повторения аналогичен способ передачи одной и той же информации по нескольким параллельным каналам связи. В этом случае необходимо иметь не менее трёх каналов связи (например, с частотным разнесением), несущие частоты которых нужно выбирать таким образом, чтобы ошибки в каналах были независимы. Достоинством таких систем являются надёжность и малое время задержки в получении информации. Основным недостатком многоканальных систем так же, как и систем с повторением, является нерациональное использование избыточности.Наиболее целесообразно избыточность используется при применении помехоустойчивых (корректирующих) кодов. При помехоустойчивом кодировании чаще всего считают, что избыточность источника сообщений на входе кодера равна 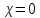 . Это обусловлено тем, что очень многие дискретные источники (например, цифровая информация на выходе ЭВМ) обладают малой избыточностью. Если избыточность первичных источников сообщений существенна, то в этих случаях по возможности стремятся ее уменьшить путём эффективного кодирования. Затем методами помехоустойчивого кодирования можно внести такую избыточность в сигнал, которая позволит достаточно простыми средствами улучшить качество приёма. Таким образом, эффективное кодирование вполне может сочетаться с помехоустойчивым. . Это обусловлено тем, что очень многие дискретные источники (например, цифровая информация на выходе ЭВМ) обладают малой избыточностью. Если избыточность первичных источников сообщений существенна, то в этих случаях по возможности стремятся ее уменьшить путём эффективного кодирования. Затем методами помехоустойчивого кодирования можно внести такую избыточность в сигнал, которая позволит достаточно простыми средствами улучшить качество приёма. Таким образом, эффективное кодирование вполне может сочетаться с помехоустойчивым.В обычном равномерном непомехоустойчивом коде число разрядов 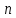 в кодовых комбинациях определяется числом сообщений и основанием кода. в кодовых комбинациях определяется числом сообщений и основанием кода.Коды, у которых все кодовые комбинации разрешены к передаче, называются простыми или равнодоступными и являются полностью безизбыточными. Безизбыточные первичные коды обладают большой «чувствительностью» к помехам. Внесение избыточности при использовании помехоустойчивых кодов обязательно связано с увеличением 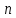 - числа разрядов (длины) кодовой комбинации. Таким образом, всё множество - числа разрядов (длины) кодовой комбинации. Таким образом, всё множество 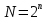 комбинаций можно разбить на два подмножества: подмножество разрешённых комбинаций, т.е. обладающих определёнными признаками, и подмножество запрещённых комбинаций, этими признаками не обладающих. комбинаций можно разбить на два подмножества: подмножество разрешённых комбинаций, т.е. обладающих определёнными признаками, и подмножество запрещённых комбинаций, этими признаками не обладающих.Помехоустойчивый код отличается от обычного тем, что в канал передаются не все кодовые комбинации 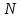 , которые можно сформировать из имеющегося числа разрядов , которые можно сформировать из имеющегося числа разрядов 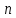 , а только их часть , а только их часть 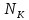 , которая составляет подмножество разрешённых комбинаций. , которая составляет подмножество разрешённых комбинаций.Если при приёме выясняется, что кодовая комбинация принадлежит к запрещённым, то это свидетельствует о наличии ошибок в комбинации, т.е. таким образом, решается задача обнаружения ошибок. При этом принятая комбинация не декодируется (не принимается решение о переданном сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами. Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т.п.). Классификация помехоустойчивых кодовВ настоящее время разработано большое количество помехоустойчивых кодов. Все эти коды подразделяются на блочные и непрерывные. К блочным относятся коды, в которых каждому сообщению относится в однозначное соответствие блок из символов. Непрерывные коды представляют непрерывную последовательность информационных и проверочных разрядов. Блочные коды разделяются на равномерные и неравномерные. Равномерные коды имеют постоянную длину кодовой комбинации. Блочные и непрерывные коды разделяются на систематические и несистематические. Под систематическим понимают код, в котором разряды могут быть разделены на проверочные и информационные. При этом их места в кодовой комбинации точно определены. Обычно в систематическом коде каждое кодовое слово начинается с информационных символов и заканчивается проверочными символами. Несистематические коды этим свойством не обладают. Кроме того коды разделяются на линейные и нелинейные. Линейными кодами считаются такими, в которых сумма по модулю “2” двух разрешенных комбинаций дает разрешенную комбинацию того же кода. Нелинейные коды отмеченным свойством не владеют. Для линейного кода применяется обозначение 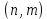 код, где код, где 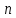 – число всех разрядов в кодовой комбинации; – число всех разрядов в кодовой комбинации; 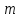 – число информационных разрядов. – число информационных разрядов.Большинство кодов, применяемых на практике, относится к линейным. Кодовое расстояниеПервые работы по корректирующим кодам принадлежат Хеммингу, который ввёл понятие минимального кодового расстояния 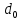 и предложил код, позволяющий однозначно указать ту позицию в кодовой комбинации, где произошла ошибка. К и предложил код, позволяющий однозначно указать ту позицию в кодовой комбинации, где произошла ошибка. К 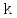 информационным элементам в коде Хемминга добавляется информационным элементам в коде Хемминга добавляется 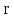 проверочных элементов для автоматического определения местоположения ошибочного символа. проверочных элементов для автоматического определения местоположения ошибочного символа.Расстояние Хемминга – характеризует степень различия кодовых комбинаций и определяется числом несовпадающих в них разрядов. Перебрав все возможные пары разрешенных комбинаций рассматриваемого кода можно найти минимальное расстояние Хемминга 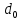 . .Минимальное расстояние 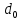 – называется кодовым расстоянием. Кодовое расстояние определяет способность кода обнаруживать и исправлять ошибки. – называется кодовым расстоянием. Кодовое расстояние определяет способность кода обнаруживать и исправлять ошибки.Чтобы код обладал свойствами обнаруживать одиночные ошибки, необходимо ввести избыточность, которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными комбинациями не менее двух. В общем случае при необходимости обнаруживать ошибки кратности 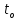 – минимальное хеммингово расстояние должно быть, по крайней мере, на единицу больше – минимальное хеммингово расстояние должно быть, по крайней мере, на единицу больше 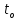 , то есть , то есть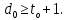 В этом случае никакая ошибка кратности не в состоянии перевести одну разрешенную комбинацию в другую. Ошибки можно не только обнаруживать, но и исправлять. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние должно быть не менее трех. В общем случае исправляемые ошибки кратности 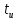 связаны с кодовым расстоянием соотношением связаны с кодовым расстоянием соотношением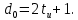 Простейший код для обнаружения однократных ошибокПростейшим способом помехоустойчивого кодирования является добавление к информационным элементам кода одного проверочного элемента. Получается код с проверкой на четность. Данный код является двоичным блочным кодом и образуется путем добавления к кодовому слову -символьного кода одного избыточного символа так, чтобы количество единиц в новом 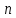 -символьном слове было четным. Код обнаруживает все ошибки нечетной кратности и не обнаруживает ошибок четной кратности. Если число информационных элементов кода равно 9 (код с параметрами -символьном слове было четным. Код обнаруживает все ошибки нечетной кратности и не обнаруживает ошибок четной кратности. Если число информационных элементов кода равно 9 (код с параметрами 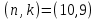 ), то вероятность необнаруженной этим кодом ошибки при независимых ошибках определяется биноминальным законом: ), то вероятность необнаруженной этим кодом ошибки при независимых ошибках определяется биноминальным законом: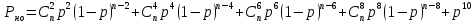 , ,где 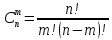 – биноминальный коэффициент; – биноминальный коэффициент; – вероятность искажения одного элемента кода. – вероятность искажения одного элемента кода.Совершим численную подстановку в формулу: 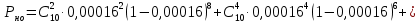 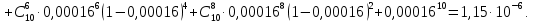 Определим избыточность кода. В кодировании избыточности определяется отношением контрольных символов 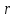 к информационным к информационным 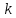 в одном слове в одном слове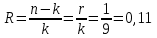 |
