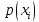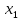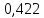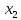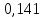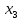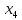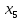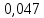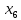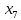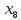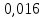Разработка структурной схемы системы связи
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
Статистическое кодированиеОптимальное статистическое кодирование обеспечивает минимизацию среднего количества кодовых символов на один элемент сообщения. Этим обеспечивается получение максимально возможного количества информации, передаваемого кодовыми комбинациями при ограниченной пропускной способности канала связи. Эффективное кодирование сообщений для передачи их по дискретному каналу без помех базируется на теореме Шеннона, которую можно сформулировать так: при производительности источника сообщений меньше пропускной способности канала связи существует способ кодирования, позволяющий передавать по каналу все сообщения, вырабатываемые источником; не существует способа кодирования, обеспечивающего передачу сообщений без их неограниченного накопления, если производительность источника сообщений больше пропускной способности канала связи. Теорема Шеннона не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый символ должен принимать значения 0 и 1 по возможности с равными вероятностями, и каждый выбор должен быть независим от значений предыдущих символов. Система связи служит для передачи сообщений от отправителя к получателю. Однако не всякое сообщение содержит информацию. Информация – это совокупность сведений об объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении. В математической теории связи (теории информации) исходят из того, что в некотором сообщении 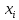 количество информации количество информации 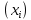 зависит не от её конкретного содержания, степени важности и т.д., а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений. зависит не от её конкретного содержания, степени важности и т.д., а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.В реальных условиях выбор конкретного сообщения производится с некоторой априорной вероятностью 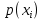 . Чем меньше эта вероятность, тем больше информации содержится в данном сообщении. . Чем меньше эта вероятность, тем больше информации содержится в данном сообщении.При определении количества информации исходят из следующих требований: Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении. Количество информации о достоверном событии ( 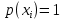 ) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении. ) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.Указанным требованиям удовлетворяет логарифмическая мера, определяемая формулой 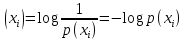 Чаще всего логарифм берется с основанием 2: 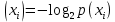 двоичных единиц информации (бит), двоичных единиц информации (бит),В теории информации чаще всего необходимо знать не количество информации 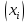 , содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений. , содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.Если имеется ансамбль (полная группа) из 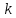 сообщений сообщений 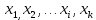 с вероятностями с вероятностями 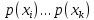 , то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений , то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений 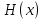 , определяется формулой , определяется формулой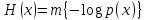 или 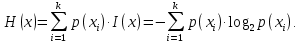 Размерность энтропии количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения. Энтропия равна нулю, если с вероятностью единица источником выдается всегда одно и тоже сообщение (в этом случае неопределенность в поведении источника сообщений отсутствует). Энтропия максимальна, если символы источника появляются независимо и с одинаковой вероятностью. Вычислим энтропию данного источника с учетом вероятностей передачи элементов “1” и “0” ( 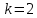 ). В нашем случае ). В нашем случае 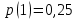 , тогда , тогда 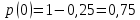 . Таким образом, энтропия источника будет: . Таким образом, энтропия источника будет: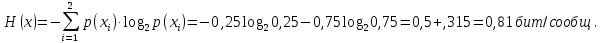 Среднее количество информации, выдаваемое источником за единицу времени, называют производительностью источника 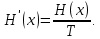 Для данного случая: 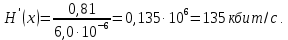 Произведем кодирование по методу Хаффмана, который работает следующим образом: На вход приходят упорядоченные по невозрастанию частот данные. Выбираются две наименьших по частоте буквы алфавита, и создается родитель (сумма двух частот этих «листков»). Потомки удаляются и вместо них записывается родитель, «ветви» родителя нумеруются: левой ветви ставится в соответствие «1», правой «0». Шаг два повторяется до тех пор, пока не будет найден главный родитель — «корень». Прежде всего перед осуществлением статистического кодирования образуем трехбуквенные комбинации, состоящие из двоичного кода 1 и 0 с соответствующими заданными вероятностями 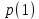 и и 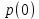 . Всего таких комбинаций будет 8. Вычислим вероятности этих трехбуквенных комбинаций: . Всего таких комбинаций будет 8. Вычислим вероятности этих трехбуквенных комбинаций: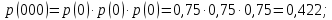 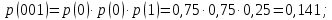 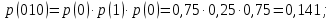 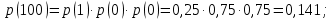 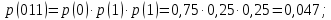 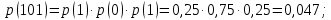 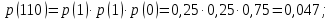 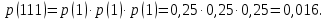 На рис. 15 представлен алгоритм Хаффмана для данного источника сообщений. 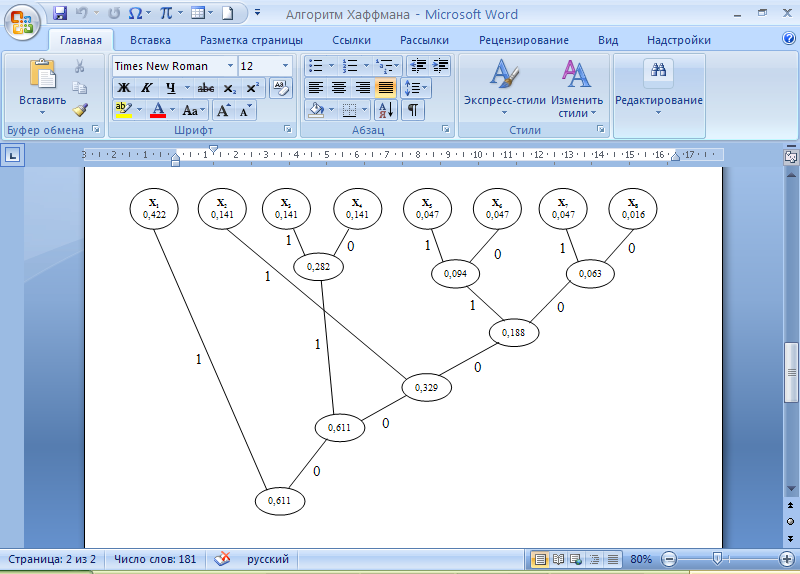 Рисунок 15. Алгоритм Хаффмана. Таблица 3
Если различные элементы сообщения имеют разную длительность, то для вычисления производительности источника надо учитывать среднюю длительность 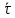 , равную математическому ожиданию величины , равную математическому ожиданию величины  : :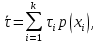 где 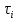 – длительность кодовой комбинации после статистического кодирования. Здесь, согласно таблице 2, – длительность кодовой комбинации после статистического кодирования. Здесь, согласно таблице 2, 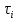 будет равна будет равна 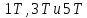 . .Производительность источника в данном случае будет: 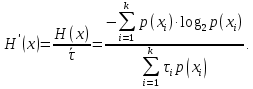 Вычислим энтропию источника: 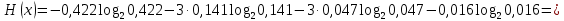 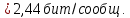 Средняя длительность будет равна 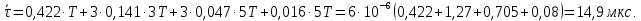 Тогда производительность источника: 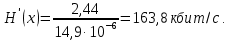 Пропускная способность двоичного канала связиДля двоичного симметричного канала ( 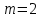 ) пропускная способность в двоичных единицах в единицу времени равна ) пропускная способность в двоичных единицах в единицу времени равна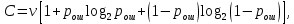 где 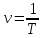 – скорость передачи сообщений (Бод), – скорость передачи сообщений (Бод), 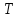 – длительность элементарного сигнала; – длительность элементарного сигнала;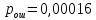 – вероятность искажения сигнала. – вероятность искажения сигнала.Рассчитаем пропускную способность для данного случая: 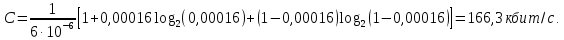 В итоге имеем пропускную способность канала равную 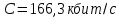 , производительность источника до оптимального кодирования , производительность источника до оптимального кодирования 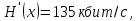 производительность источника после оптимального кодирования производительность источника после оптимального кодирования 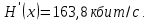 Сравнивая данные величины, приходим к выводу, что передача информации от данного источника возможна как до кодирования, так и после него. ЗаключениеВ курсовой работе разработана структурная схема системы связи для передачи, как двоичных данных, так и аналоговых сигналов используя, аналого-цифровой преобразователь. Передача осуществляется когерентной дискретной фазовой модуляцией. В работе показано, что данный вид модуляции обладает наибольшей помехоустойчивостью. При аддитивной помехи типа «гауссовского белого шума» вероятность ошибки в приеме сигнала составляет 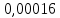 . При введении статистического кодера достигается увеличение производительности источника, за счет введения неравномерных кодов. Наиболее эффективным алгоритмом статистического кодирования является алгоритм Хаффмана. . При введении статистического кодера достигается увеличение производительности источника, за счет введения неравномерных кодов. Наиболее эффективным алгоритмом статистического кодирования является алгоритм Хаффмана.Пропускная способность канала связи позволяет передачу данных, как со статистическим кодером, так и без него. Введение помехозащитного кодека увеличивает избыточность кода, но снижает вероятность ошибки в приеме сигнала. Показано что приемник Котельникова обладает потенциальной помехоустойчивостью. Также потенциальную помехоустойчивость можно достигнуть, используя когерентный прием с оптимальным фильтром. Совершенствование разработанной системы связи требует следующих улучшений: Переход на квадратурную амплитудную модуляцию, при которой одновременно происходит изменение фазы и амплитуды, что позволяет больше передавать информации. Использование когерентного приема с оптимальной фильтрацией, для увеличения помехоустойчивости. Увеличение уровней квантования расширит спектр передаваемого аналогового сигнала. ЛитератураМакаров А.А., Чернецкий Г.А. Теория электрической связи: Методические указания. Задание на курсовую работу. – Новосибирск, СибГУТИ , 2007. – 40 с. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. Учебник для вузов / – 2-е изд. перераб. и доп. – М.: Радио и связь, 1986. – 304 с. Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи: Учебник для вузов связи / Под ред. Д.Д. Кловского. – М.: Радио и связь, 1999. – 432 с. Макаров А.А., Чиненков Л.А. Основы теории помехоустойчивости дискретных сигналов. Учеб. пособие. – Новосибирск, СибГАТИ, 1997. – 42 с. Макаров А.А., Чиненков Л.А. Основы теории передачи информации. Учеб. пособие. – Новосибирск, СибГУТИ, 1998. – 40 с. Макаров А.А., Прибылов В.П. Помехоустойчивое кодирование: Монография/СибГУТИ. – Новосибирск, 2005. – 186 с. Филиппов Б.И. Теория электрической связи. Учеб. пособие. – Новосибирск, СибГУТИ, 2011. – 283 с. Клюев Л.Л. Теория электрической связи. – Мн.: Дизайн ПРО, 1998. – 336 с. Шувалов В.П. Крук Б.И. Попантонолуло В.Н. Телекоммуникационные системы и сети. Том 1. Современные технологии. – М: Горячая линия-Телеком, 2003 – 647 с. 
 |