Разработка структурной схемы системы связи
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
Сравнение выбранной схемы приемника с оптимальным приемникомОптимальный приемник КотельниковаЦелью оптимального приема (так же, как и помехоустойчивого кодирования) является повышение верности принимаемых сообщений. Если при помехоустойчивом кодировании эта задача решается выбором кода, который определяет структуры кодера и декодера, то при оптимальном приеме задача решается выбором структуры приемника (демодулятора). Структура приемника, удовлетворяющая заданному критерию оптимальности, называется оптимальной, а приемник — оптимальным. Приемник анализирует смесь элемента сигнала и помехи в течение единичного интервала времени и принимает решение о том, какой из возможных сигналов (символов) присутствует в этой смеси. С приходом следующего элемента анализ повторяется. Этот способ приема получил название посимвольного. Возможными видами сигналов могут быть: двоичные AM, ФМ, ОФМ и ЧМ сигналы; многопозиционные ( 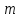 -ичные) сигналы с ФМ, ОФМ и с квадратурной амплитудной модуляцией (КАМ). Обычно полагают, что помеха, возникающая в линии связи, является нормальным белым шумом. -ичные) сигналы с ФМ, ОФМ и с квадратурной амплитудной модуляцией (КАМ). Обычно полагают, что помеха, возникающая в линии связи, является нормальным белым шумом.При посимвольном приеме решаются следующие задачи: задача обнаружения сигнала; задача различения одного из 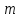 сигналов. сигналов.Первая задача возникает при приеме сигналов, соответствующих элементам двоичного кодового слова, которые равны 0 или 1. Приемник, анализируя смесь сигнала и шума в течение длительности единичного интервала, дает ответ: есть на входе сигнал или его нет. Вторая задача возникает: а) при приеме элементов двоичных сигналов, которым соответствуют элементы двоичного кодового слова 1, -1; б) при приеме элементов -ичных сигналов, соответствующих символам 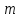 -ичных кодовых слов. Впервые задача оптимального приема была поставлена, и решена в 1946 г. выдающимся русским ученым В. А. Котельниковым. -ичных кодовых слов. Впервые задача оптимального приема была поставлена, и решена в 1946 г. выдающимся русским ученым В. А. Котельниковым.Рассмотрим систем у передачи информации, в которой передаются два сигнала 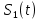 и и 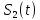 одинаковой длительности одинаковой длительности 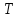 , произвольной (но известной) формы, априорные вероятности , произвольной (но известной) формы, априорные вероятности 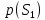 и и 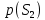 ; помехи в канале флуктуационные, ФВП которых имеет вид гауссовского закона ; помехи в канале флуктуационные, ФВП которых имеет вид гауссовского закона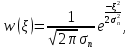 где 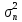 – дисперсия (мощность) помех. – дисперсия (мощность) помех.Задан критерий оптимального приема: идеальный наблюдатель (или наблюдатель В.А.Котельникова), который минимизирует среднюю вероятность ошибки 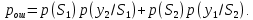 Найдем оптимальное правило решения и структурную схему оптимального приемника (оптимального РУ) для указанных выше условий передачи сигналов 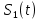 и и 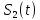 . .Для решения задачи используем общее для приемников двоичных сигналов правило решения ( 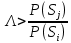 ). В рассматриваемом случае ). В рассматриваемом случае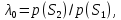 Если 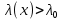 , то принимается решение в пользу сигнала , то принимается решение в пользу сигнала 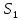 , иначе , иначе 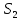 . .Для упрощения решения положим вначале, что 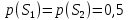 ;тогда ;тогда 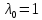 . В этом случае критерий идеального наблюдателя совпадает с критерием максимального правдоподобия. . В этом случае критерий идеального наблюдателя совпадает с критерием максимального правдоподобия.Для определения функции правдоподобия 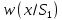 и и 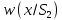 , которые при произвольной длительности сигналов , которые при произвольной длительности сигналов 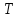 будут многомерными. Предположим, что на вход приемника поступает сигнал (рис. 6) будут многомерными. Предположим, что на вход приемника поступает сигнал (рис. 6)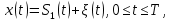 Возьмем 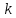 отсчетов сигнала отсчетов сигнала 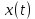 через одинаковые интервалы через одинаковые интервалы 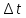 , равные интервалу корреляции помехи , равные интервалу корреляции помехи 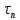 . . В первом сечении 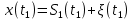 ; ;Во втором случае 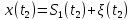 ; ;… В k-ом сечении 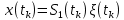 . .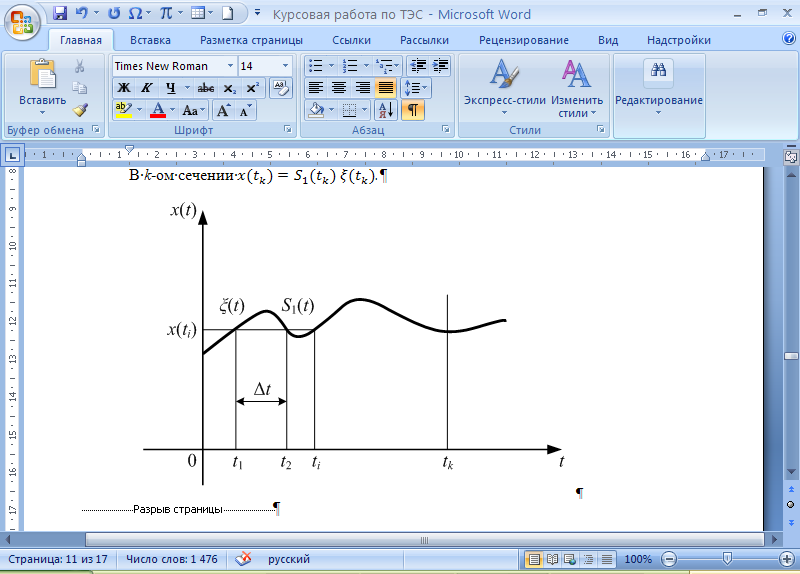 Рисунок 6. Сигнал на входе приемника Рассмотрим отсчетные значения суммы сигнала 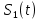 и помехи и помехи 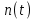 в различных сечениях в различных сечениях 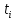 . Т.к. расстояние между сечениями равно интервалу корреляции помехи, эти сечения не коррелированны. А т.к. помеха распределена по гауссовскому закону, то эти сечения также и независимы. . Т.к. расстояние между сечениями равно интервалу корреляции помехи, эти сечения не коррелированны. А т.к. помеха распределена по гауссовскому закону, то эти сечения также и независимы.Плотность вероятности случайной величины 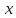 в k-ом сечении при известном сигнале в k-ом сечении при известном сигнале 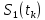 определяется выражением определяется выражением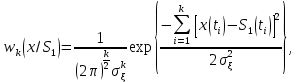 а k-мерная плотность вероятности благодаря независимости сечения будет равна произведению одномерных плотностей вероятностей различных сечений. 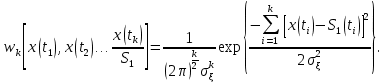 Аналогичное выражение можно записать для сигнала 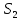 , заменив в последнем выражении , заменив в последнем выражении 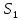 на на 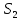 . .Тогда отношение правдоподобия 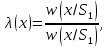 и, согласно правилу решения 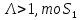 , ,если вычисленное значение 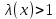 (у нас (у нас 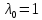 ), то приемник должен выдать сигнал ), то приемник должен выдать сигнал 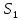 , в противоположном случае – сигнал , в противоположном случае – сигнал 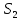 . Отсюда получаем оптимальное правило решения в виде неравенства . Отсюда получаем оптимальное правило решения в виде неравенства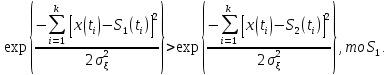 Прологарифмируем это выражение: 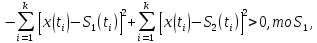 или в другом виде 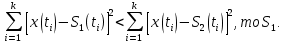 Таким образом, оптимальный приемник (идеальный приемник Котельникова) работает следующим образом: определяется среднеквадратическое отклонение поступившего на его вход сигнала 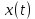 от обоих ожидаемых сигна-лов и выносится решение пользу того сигнала, где это среднеквадратическое отклонение меньше. от обоих ожидаемых сигна-лов и выносится решение пользу того сигнала, где это среднеквадратическое отклонение меньше. Если при вычислении условных вероятностей расстояние между сечениями 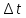 устремить к нулю, т.е. сделать устремить к нулю, т.е. сделать 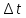 меньше интервала корреляции помехи, работа приемника не улучшиться, т.к. соседние сечения будут сильно коррелированы, но и не ухудшится. меньше интервала корреляции помехи, работа приемника не улучшиться, т.к. соседние сечения будут сильно коррелированы, но и не ухудшится.В интегральной форме получим 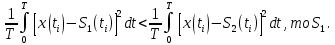 или более компактно (черта означает усреднение по времени)   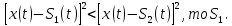 В соответствии с полученным правилом решения структурная схема приемника будет иметь вид, приведенный на рис. 7. Схема содержит два генератора опорных сигналов: 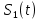 и и 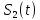 , которые генерируют точно такие же сигналы, которые могут поступить на вход приемника, а также два вычитающих устройства, два квадратора, два интегратора и схему сравнения, которая, в соответствии с неравенством, выдает сигналы , которые генерируют точно такие же сигналы, которые могут поступить на вход приемника, а также два вычитающих устройства, два квадратора, два интегратора и схему сравнения, которая, в соответствии с неравенством, выдает сигналы 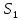 и и 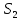 . .При этом следует подчеркнуть, что приемник Котельникова, как и многие другие приемники дискретных сигналов, выдает на выходе сигналы (решения), форма которых обычно отличается от формы сигналов в линии связи 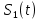 и и 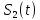 . Например, в линии связи эти сигналы могут представлять собой импульсы дискретной частотной модуляции, а на выходе приемника получаем импульсы постоянного тока прямоугольной формы. . Например, в линии связи эти сигналы могут представлять собой импульсы дискретной частотной модуляции, а на выходе приемника получаем импульсы постоянного тока прямоугольной формы.Если вероятности передачи сигналов 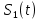 и и 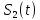 не одинаковы, т.е. не одинаковы, т.е. 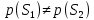 , то неравенство принимает несколько другой вид: , то неравенство принимает несколько другой вид:  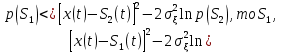 а в структурной схеме перед схемой сравнения добавляются выравнивающие устройства – В (показаны пунктиром). Может показаться, что приведенная на рисунке схема приемника достаточно проста. Однако применяющиеся в схеме местные генераторы 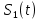 и и 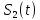 должны выдавать сигналы, по форме идентичные передаваемым сигналам, ожидаемым на входе приемника; поэтому эти генераторы должны синхронизироваться приходящими сигналами, а это сделать довольно трудно. должны выдавать сигналы, по форме идентичные передаваемым сигналам, ожидаемым на входе приемника; поэтому эти генераторы должны синхронизироваться приходящими сигналами, а это сделать довольно трудно.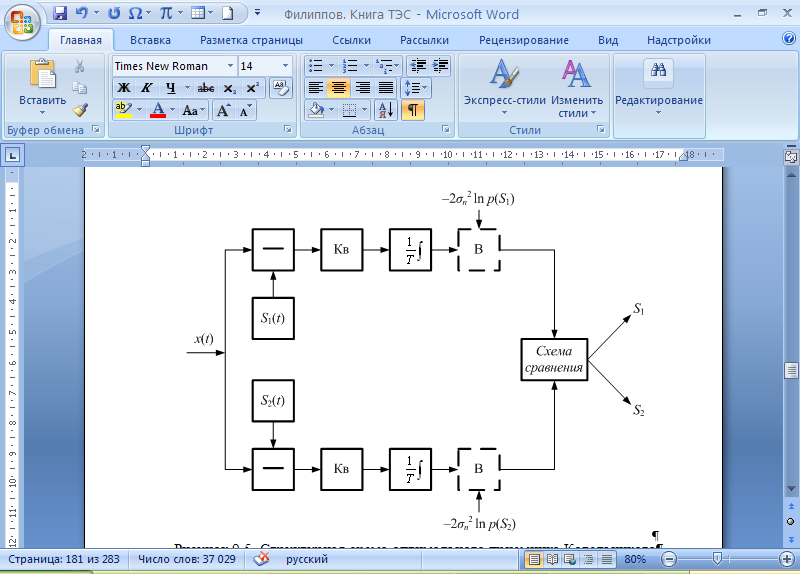 Рисунок 7. Структурная схема оптимального приемника Котельникова |
