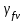разработкаа вариантов мостового перехода. Разработка
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Расчет главной балкиОпределение расчетных усилийПостоянная нагрузка на пролётное строение складывается из собственного веса конструкции и веса мостового полотна. Нормативная нагрузка на 1 погонный метр главной балки определяется, кН/м: - от собственного веса: 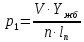 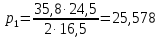 - от веса мостового полотна с ездой на балласте: 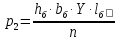 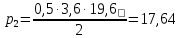 где: V и lп – объем железобетона и полная длина пролетного строения; n – число главных балок; hб – толщина балластного слоя; bб – ширина балластного корыта равная 3,6 м, для однопутных мостов. Коэффициенты надежности по нагрузке f для постоянных нагрузок при расчете на прочность принимаются: для собственного веса конструкции f1 = 1,1 (0,9); для веса мостового полотна с ездой на балласте f2 = 1,3 (0,9); Из двух указанных значений коэффициентов надежности по нагрузке принимается то, которое создает наиболее невыгодное суммарное воздействие постоянной и временной нагрузки. При расчете на прочность нормативная временная нагрузка по схеме СК, при однозначной линии влияния используется в расчетах в виде: эквивалентной нагрузки νК, кН/м, соответствующей наиболее тяжелой нагрузки от состава с локомотивом; распределенной нагрузки 9,81К, кН/м, от веса груженых вагонов состава; нагрузки 13,7 кН/м от порожнего подвижного состава. Однозначные линии влияния и отдельные участки двухзначных линий влияния загружаются эквивалентной нагрузкой νК. Нормативная временная вертикальная нагрузка на одну главную балку принимается равной 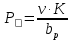 где,  - эквивалентная нагрузка класса К=1 - эквивалентная нагрузка класса К=1К – класс заданной нагрузки Интенсивность эквивалентной нагрузки зависит от параметров и , определяющих положение вершины и длину загружаемого участка линии влияния (𝜔- площадь линии влияния) (рисунок 3). Нормативная временная нагрузка умножается при расчёте на прочность на коэффициент надёжности по нагрузке 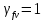 , который зависит от длины загружения линии влияния , который зависит от длины загружения линии влияния 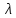 , м: , м:
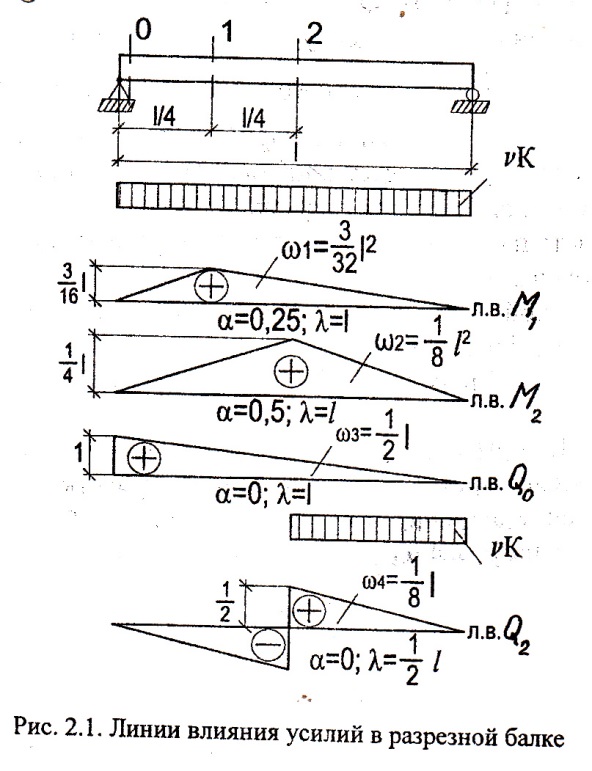 Рисунок 3 Линии влияния усилий в разрезной балке 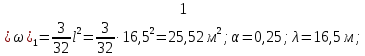 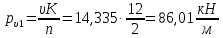 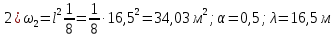 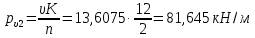 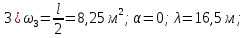 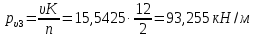 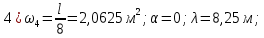 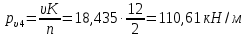 Расчетное усилие от постоянных нагрузок определяется как произведение суммарной интенсивности всех нагрузок на алгебраическую сумму площадей всех участков линии влияния: 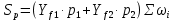 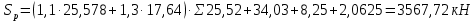 Усилие от временной вертикальной нагрузки (положительное или отрицательное) определяется как сумма произведений интенсивности нагрузки с учетом динамического воздействия на площадь участка соответствующего знака: 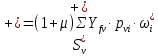 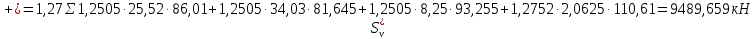 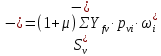 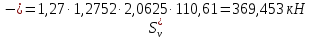 Динамический коэффициент к нагрузкам от подвижного состава определяется по формуле: 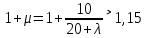 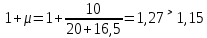 где λ – длина пролета l или длина загружения линии влияния L, если она больше длины пролета. Полные усилия в сечениях балки (рис. 3) при расчете на прочность определяются как: 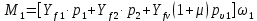 ; ;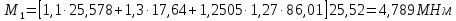 ; ;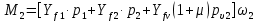 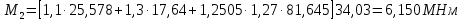 ; ;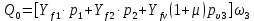 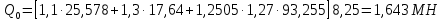 ; ;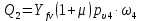 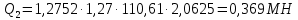 Усилия при расчете на трещиностойкость определяются от действия на конструкцию нормативных нагрузок. Коэффициенты надежности по нагрузке принимаются 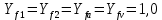 ; ; 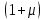 =1,0 =1,0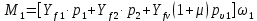 ; ;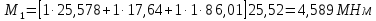 ; ;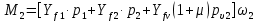 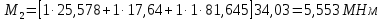 ; ;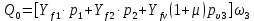 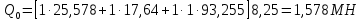 ; ;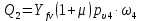 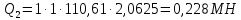 По результатам вычислений построены эпюры M и Q (рисунок 4) 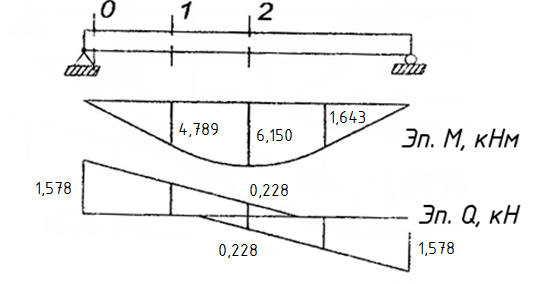 Рисунок 4 Огибающие эпюры в разрезной балке. Расчет на прочность по изгибающему моменту Расчету балки предшествует выбор типа поперечного сечения и назначение основных размеров (высота, ширина плиты, толщина ребра). Поперечное сечение главной балки имеет тавровую форму. Действительная форма поперечного сечения приводится к расчётной форме. Максимальная ширина плиты сжатой зоны тавровых и коробчатых сечений, учитываемая в расчёте, ограничена длиной свесов плиты, которая не должна быть больше 6 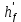 ( (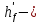 приведенная (средняя) толщина плиты при фактической ширине плиты приведенная (средняя) толщина плиты при фактической ширине плиты 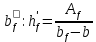 ). ).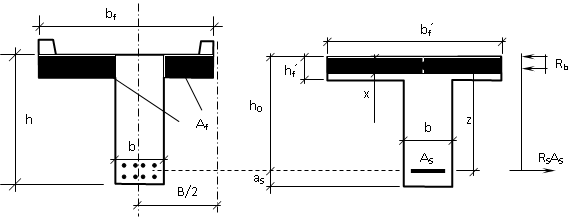 Рисунок 5. Расчетная схема поперечных сечений главной балки. hf’ = 0.2 м, bf = b’f =2.09 м, b = 0,5 м. Центр тяжести арматуры ориентировочно назначается на расстоянии as = 0,15 м от нижней грани пояса балки. Полезная высота сечения: 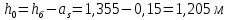 Расчет на прочность по изгибающему моменту производим для наиболее нагруженного сечения. Определяем в первом приближении высоту сжатой зоны бетона 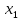 при действии расчетного момента M2: при действии расчетного момента M2: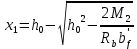 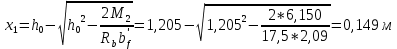 т. к. x1 < hf’ то сечение рассчитывается как прямоугольное. Необходимая площадь арматуры определяется как: 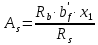 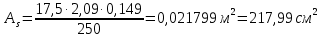 Количество стержней арматуры: 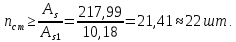 где As1 - площадь сечения одного стержня (принимаем рабочую арматуру класса A-II 36 мм, As1 = 10,18 см2); Уточним площади арматуры: 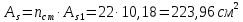 После уточнения площади арматуры с учетом принятого количества стержней определяется высота сжатой зоны: 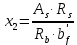 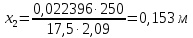 где As- уточненная площадь арматуры. Условие прочности сечения по изгибающему моменту записывается в виде: 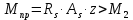 , ,где, 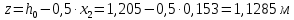 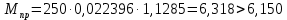 Проверка выполняется, сечение из условия прочности подобрано правильно. Расчет на трещиностойкость по касательным напряжениям Расчет по касательным напряжениям выполняется в предположении упругой работы конструкции, но без учета бетона растянутой зоны. В расчете ограничивается величина касательных напряжений, действующих по нейтральной оси сечения. Касательные напряжения могут быть определены приближенно по формуле: 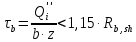 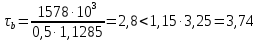 где 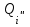 - поперечная сила в рассматриваемом сечении от нормативных нагрузок (принимаем - поперечная сила в рассматриваемом сечении от нормативных нагрузок (принимаем 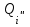 = Q0 = = Q0 = 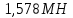 ) ) Rb,sh – расчетное сопротивление бетона на скалывание при изгибе, для B 35 = 3,25 МПа Условие выполняется, прочность обеспечена. Расчет на прочность по поперечной силе. 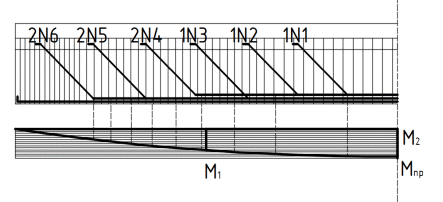 Рисунок. 6. Эпюра моментов в балке и схема отгибов рабочей арматуре При расчете изгибаемых железобетонных элементов на прочность по поперечной силе предполагается, что в предельном состоянии образуется наклонная трещина в бетоне, разделяющая элемент на две части. Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны. Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих моментов. Для этого точки отгибов сносим на эпюру М, следя за тем, чтобы предельный момент для оставшихся стержней рабочей арматуры не был меньше расчетного момента в сечении. При необходимости можно отгибать стержни группами по два-три в одном сечении. Эпюра предельных моментов (эпюра материалов) должна быть во всех сечениях объемлющей по отношению к эпюре расчетных моментов. Для построения эпюры материалов используем приближенную зависимость, считая, что предельный момент, воспринимаемый сечением с одним стержнем рабочей арматуры, равен 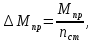 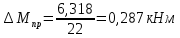 где 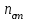 - количество стержней рабочей арматуры в среднем (2) сечении. - количество стержней рабочей арматуры в среднем (2) сечении.Графически 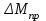 получаем делением максимальной ординаты горизонтальными линиями на равные отрезки, число которых соответствует количеству стержней рабочей арматуры. Точки пересечения горизонтальных линий с эпюрой расчетных моментов определяют места возможного отгиба стержней. Наклонные стержни должны равномерно армировать ребро главной балки. На всем участке расположения отогнутой арматуры любое произвольно выбранное вертикальное сечение должен пересекать хотя бы один наклонный стержень. Угол наклона стержней получаем делением максимальной ординаты горизонтальными линиями на равные отрезки, число которых соответствует количеству стержней рабочей арматуры. Точки пересечения горизонтальных линий с эпюрой расчетных моментов определяют места возможного отгиба стержней. Наклонные стержни должны равномерно армировать ребро главной балки. На всем участке расположения отогнутой арматуры любое произвольно выбранное вертикальное сечение должен пересекать хотя бы один наклонный стержень. Угол наклона стержней 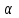 к оси балки обычно принимают равным к оси балки обычно принимают равным 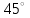 , но не более , но не более 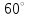 и не менее и не менее 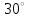 . .Не менее 1/3 стержней рабочей арматуры должны доводиться без отгибов до опоры. Эпюра материалов представлена на рис. 6. Проверка прочности наклонного сечения на действие поперечной силы производится из условия: 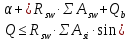 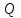 - максимальное значение поперечной силы от внешних нагрузок, расположенных по одну сторону от наклонного сечения; - максимальное значение поперечной силы от внешних нагрузок, расположенных по одну сторону от наклонного сечения; - расчетное сопротивление арматуры отогнутых стержней принятого класса А-II - расчетное сопротивление арматуры отогнутых стержней принятого класса А-II и и  - площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей одного хомута, пересекающих наклонное сечение; - площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей одного хомута, пересекающих наклонное сечение;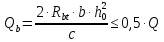 - поперечное усилие, передаваемое на бетон сжатой зоны сечения, где - поперечное усилие, передаваемое на бетон сжатой зоны сечения, где 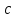 - длина горизонтальной проекции сечения. - длина горизонтальной проекции сечения.В курсовом проекте можно ограничиться проверкой наклонных сечений непосредственно у опоры и в середине пролета. При этом наклонное сечение должно располагаться в пределах постоянной толщины ребра. На приопорных участках длиной 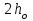 наклонное сечение составляет с продольной осью балки угол 45°, длина его горизонтальной проекции равна наклонное сечение составляет с продольной осью балки угол 45°, длина его горизонтальной проекции равна 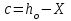 . На других участках наклонные сечения проверяются при длине проекции . На других участках наклонные сечения проверяются при длине проекции 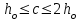 . Для сечения в середине пролета можно принять . Для сечения в середине пролета можно принять 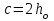 . Схема к расчету представлена на рисунке 7. . Схема к расчету представлена на рисунке 7.Располагая схемой размещения отогнутых стержней, определим количество стержней, пересекающих наклонное сечение и соответственно суммарную площадь 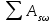 . .Для определения суммарной площади поперечных сечений хомутов 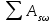 , пересекающих наклонное сечение, используем следующие рекомендации. , пересекающих наклонное сечение, используем следующие рекомендации.Площадь всех ветвей одного хомута определяется 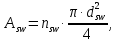 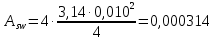 где 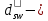 диаметр хомута (на концевых участках балок диаметр хомута (на концевых участках балок 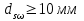 ); );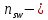 число ветвей одного хомута. число ветвей одного хомута.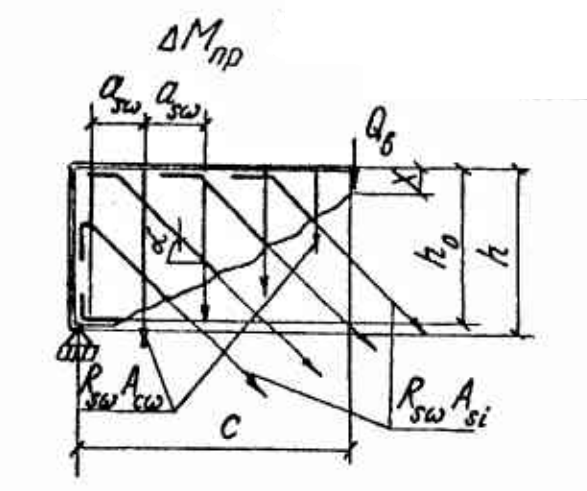 Рисунок 7. Схема к расчету главной балки из обычного железобетона. Для середины пролета: 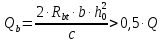 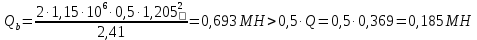 𝑄 = 1.643 МН ≤ 200∙4∙0,001018 ∙ sin45 + 160 ∙ 20∙ 0,000314 + 0,185 = 1,698 МН где, 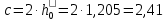 Условие выполняется, прочность обеспечена.  Для опорного сечения: 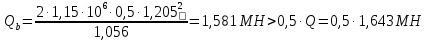 𝑄 = 0,369 МН ≤ 200∙2∙0,001018 ∙ sin45 + 160 ∙ 10∙ 0,000314 + 0,185 = 0.849 МН где, 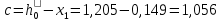 Условие выполнено. Прочность по наклонному сечению обеспечена. ВыводПо заданию курсовой работы были составлены три варианта мостового перехода, сделано их технико-экономическое сравнение, выполнен их чертёж с указанием основных размеров и отметок. Так же выполнен расчёт пролётного строения из ненапряжённого железобетона. Выполнен чертёж балки пролётного строения: фасад, план, сечения на опоре и в пролёте, разрезы, показана схема армирования. Библиографический списокСП 35.13330.2011. Мосты и трубы. – М.: НИИТС , 2011. – 339 с. Проектирование железобетонных мостов. Разработка вариантов: учеб. пособие / Г. И. Богданов, В. Н. Смирнов. – Изд. 2-е, перераб. и доп. – СПб.: ПГУПС, 2012. – 134 с. Проектирование и расчет балочных пролетных строений железобетонных мостов: учеб. пособие. / Карапетов Э.С. – СПб.: ПГУПС, 2013. – 53 с. Составление вариантов металлического моста: учеб. пособие / Владимирский С. Р., Козьмин Ю. Г. – СПб: ПГУПС, 1996. – 99 с. Мосты и тоннели на железных дорогах: учебник для вузов / В. О. Осипов, В. Г. Храпов, Б. В. Бобриков и др.; Под ред. В. О. Осипова. – М.: Транспорт, 1988. – 367 с. СП 24.13330.2011. Свайные фундаменты. – Приложение 1 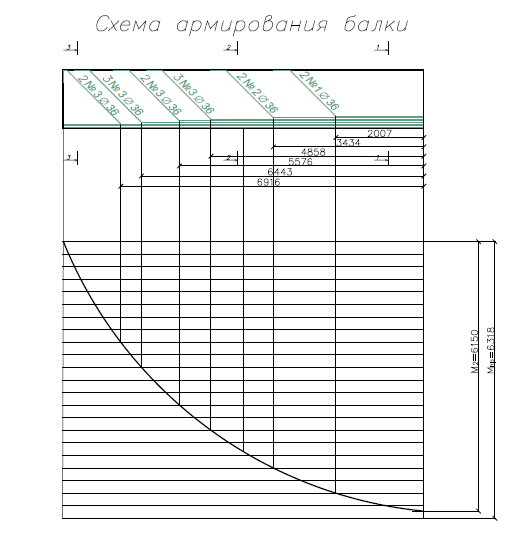 |