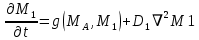Ибрахим Саид 4 тему (1). Развитие математических методов теории эволюции 3 Роль компьютера в математическом анализе жизни 4
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
Роль компьютера в математическом анализе жизниПо окончании Второй мировой войны в Великобритании и США появились первые компьютеры. Два союзных государства начали борьбу за право называться их родиной, и толчком к началу этого соперничества стала возможность использования компьютеров прежде всего в военных целях. Новая техника создавалась для борьбы с общим врагом – СССР. Напомним, что именно эти годы стали началом эпохи холодной войны, и изменение политической обстановки повлияло на работы ученых во всем мире. Хотя историки науки считают, что первый компьютер, известный как ENIAC1 был сконструирован в США в 1946 году, сегодня мы знаем, что до него существовал «Колосс», созданный в Великобритании в 1944 году. В 1950 году Алан Тьюринг, один из самых лучших британских ученых XX столетия, сконструировал компьютер АСЕ2 в Национальной физической лаборатории. Этот компьютер имел возможности хранения данных и работы программ, весьма схожие с возможностями первых компьютеров Macintosh, созданных только в 1980-е годы. Компьютер Тьюринга был британским конкурентом американского EDVAC3, созданного на базе EN1AC. В конструировании EDVAC участвовал еще один ученый того времени – Джон фон Нейман.  Рисунок 2 «Колосс» – первый компьютер в истории, построенный в Великобритании в 1944 году Британским ответом на EDYAC стал EDSAC4 – еще один компьютер с похожими характеристиками. В это же время в США был сконструирован UNIVAC5 – прямой потомок ENIAC и EDVAC. Изготовившая его компания Remington Road стала первым в мире производителем коммерческих компьютеров. Открытия Алана ТьюрингаВ 1948 году в Университете Манчестера находился один из самых мощных компьютеров того времени, а в 1951 году университет получил компьютер Ferranti Mark 1, на котором работал Тьюринг. С 1952 года до своей смерти в 1954 году Тьюринг был одним из первых ученых, кто использовал компьютер для математического моделирования биологических задач.  Рисунок 3 Компьютер Ferranti Mark I, на котором работал Алан Тьюринг (на фото справа) В то время Тьюринга очень интересовало математическое изучение морфогенеза. Одна из самых любопытных задач этой дисциплины заключается в том, чтобы объяснить, как живые организмы обретают конечную форму: почему ветви деревьев образуют именно такую структуру, почему членистоногие словно состоят из отдельных кусочков, а кольчатые черви – из колец. Еще одна классическая задача морфогенеза заключается в изучении узоров, например, на коже некоторых позвоночных – полосок у зебр или круглых пятен у далматинцев. Тьюринг первым попытался решить биологические задачи с помощью компьютера, став одним из пионеров вычислительной биоматематики. Таким образом, его исследования придали этой дисциплине более прикладной характер, сблизив ее с привычными биологическими исследованиями в лаборатории. Биологи и другие ученые под влиянием работ Тьюринга также начали изучать жизнь с математической точки зрения. Подобные исследования проводились в разные годы XX века; проводятся они и сейчас. Кроме того, Тьюринг открыл новую область математической биологии, предложив первую математическую теорию морфогенеза. В одной из своих работ для анализа формы растений он использовал числа Фибоначчи. Последовательность Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. образуется по следующему правилу: если принять первое число Фибоначчи, а1, равным 0, второе число, а2, равным 1, то каждое последующее число будет определяться как сумма двух предыдущих. Иными словами, аn = аn-1+ аn-2. Любопытно, что числа Фибоначчи описывают количество лепестков цветов, расположение чешуек шишек и листьев растений.  Рисунок 4 Число спиралей на этой шишке в каждом направлении (8 и 13 соответственно) выражается последовательными числами Фибоначчи Эта особенность растений получила название филлотаксиса Фибоначчи. Так, числа Фибоначчи описывают расположение листьев растений, при котором их освещенность будет оптимальной. Представьте, что лист соперничает с соседними за доступ к солнечному свету. Каким будет оптимальное расположение листьев, обеспечивающее наибольшую освещенность каждого листа? Ответ дает последовательность Фибоначчи. Продолжив исследования, Тьюринг совершил свое самое знаменитое открытие в этой области – он создал математическую модель «реакция – диффузия». Свои идеи ученый изложил в статье «химическая основа морфогенеза», опубликованной в престижном научном журнале Лондонского королевского общества в 1952 году. Тьюринг был математиком, а не биологом, поэтому он попытался объяснить интересовавшее его явление с помощью дифференциальных уравнений. Он задался вопросом: каким образом в однородной ткани клеток, в зачаточном состоянии очень похожих друг на друга, например, клеток кожи позвоночных, образуются полоски или пятна? С биологической точки зрения эти полоски или пятна – проявление различий между пигментными и непигментными клетками. Как следствие, полоски на шкуре зебры будут результатом нарушения изначального единообразия зародышевых клеток кожи. Тьюринга интересовал биологический механизм, ведущий к появлению подобных узоров. Ученый предполагал, что полученный узор представляет собой нестабильное состояние, поскольку стабильным состоянием является единообразие зародышевых клеток без характерного узора. С помощью компьютера Ferranti Mark I Тьюринг провел ряд экспериментов по моделированию и доказал, что полученный узор на коже зависит от значений параметров математической модели.  Рисунок 5 Полоски на шкуре зебры – один из примеров, описываемых уравнениями «реакция – диффузия» Тьюринга Параметр математической модели – это значение, соответствующее какому-либо свойству, которое нельзя оценить напрямую, в ходе наблюдений. Тьюринг выявил несколько закономерностей, очень похожих на те, что описывают распределение щупалец гидры или расположение лепестков цветка. Предположив, что клетки имеют круглую форму, Тьюринг смоделировал многоклеточный зародыш – бластулу. Бластула – один из этапов развития зародыша, на котором уже можно заметить появление узоров. Тьюринг изучил зародыши амфибий и ежей, которые сегодня благодаря своим особым свойствам широко используются в качестве моделей при изучении морфогенеза. Ученый предположил, что узоры образуются в результате процессов реакции – диффузии. Согласно его гипотезе, в зародышевой ткани, то есть в группе клеток, сгруппированных на плоскости, будут присутствовать пигментные клетки, продуцирующие вещество морфоген. Как только молекулы этого загадочного вещества распространятся в результате диффузии по зародышевой ткани, они вступают между собой в реакцию. Распределение продуктов этой химической реакции определяет так называемое поле концентраций – отпечаток, согласно которому и формируется узор зародышевых клеток. Следовательно, полоски, пятна и любые другие узоры, которые мы можем увидеть на шкуре животных, есть не более чем реплики поля концентраций. Мы не будем рассматривать знаменитые уравнения реакции – диффузии Тьюринга во всех подробностях, а только приведем их:
Эти выражения объясняют, как с течением времени изменяется объем или концентрация двух веществ, предложенных Тьюрингом, которые он назвал морфогеном- активатором (МА) и морфогеном-ингибитором (М1). Как мы уже отмечали, эти два вещества производятся только пигментными клетками. В свою очередь, f(MA, М1) и g(MA, М1) – две функции, обозначающие реакцию между активатором и ингибитором, а выражения 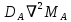 и и 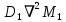 указывают, как эти два класса морфогенов распространяются по ткани. Так, когда морфогены высвобождаются пигментными клетками, начинается процесс их диффузии, подобный диффузии песчинок сахара в стакане с водой. По Тьюрингу, морфоген-активатор стимулирует воспроизводство себя самого и морфогена-ингибитора. Еще одна любопытная особенность этой реакции заключается в том, что морфоген-ингибитор распространяется на большее расстояние, чем морфоген-активатор. Расстояния, на которые распространяются морфогены, зависят от DА и D1 – коэффициентов диффузии морфогенов – активатора и ингибитора соответственно. указывают, как эти два класса морфогенов распространяются по ткани. Так, когда морфогены высвобождаются пигментными клетками, начинается процесс их диффузии, подобный диффузии песчинок сахара в стакане с водой. По Тьюрингу, морфоген-активатор стимулирует воспроизводство себя самого и морфогена-ингибитора. Еще одна любопытная особенность этой реакции заключается в том, что морфоген-ингибитор распространяется на большее расстояние, чем морфоген-активатор. Расстояния, на которые распространяются морфогены, зависят от DА и D1 – коэффициентов диффузии морфогенов – активатора и ингибитора соответственно. В 1954 году, в возрасте 41 года, Алан Тьюринг покончил с собой. Так оборвалась жизнь одного из величайших ученых XX века. Его гениальность доказывает и тот факт, что химические вещества, существование которых он предсказал математически (так называемые морфогены), были открыты экспериментально лишь много лет спустя, в начале 1990-х. Кроме того, некоторые узоры из изученных Тьюрингом на компьютере Ferranti Mark I были обнаружены на чешуе рыбы полукруглый ангел, или Pomacanthus semicirculatus. В настоящее время морфогенез – одна из областей математической биологии, и удивительным путем, на который первым вступил Алан Тьюринг, проследовали такие видные ученые, как Мюррей, Мейнхардт и другие. |