Реферат Неевклидовы Геометрии. Медведева Е.Б. Реферат по дисциплине Основы математической обработки информации Неевклидовы геометрии Выполнил студент
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА И.Г. ПЕТРОВСКОГО» (БГУ) Факультет педагогики и психологии РЕФЕРАТ по дисциплине Основы математической обработки информации Неевклидовы геометрии Выполнил студент: Факультет: Педагогики и психологии Направление подготовки: 44.03.03 Специальное (дефектологическое) образование Профиль подготовки Логопедия Форма обучения: заочная 1 курса, I группы Медведева Екатерина Борисовна ____________________ (подпись) Проверил: к.ф.-м.н, профессор Тонких А.П. ___________________ (подпись) Брянск 2020 г. Содержание
Введение Геометрия - это одна из древнейших наук. Исследовать различные пространственные формы издавна побуждало людей их практическая деятельность. Древнегреческий ученый Эдем Родосский в IV веке до нашей эры писал: «Геометрия была открыта египтянами, и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшей границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребности человека». Многие первоначальные геометрические сведения получили также шумеро-вавилонские, китайские и другие ученые древнейших времен. Устанавливались они сначала только опытным путем, без логических доказательств. Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны. В III веке до нашей эры греческий ученый Евклид привел в систему известные ему геометрические сведения в большом сочинении «Начала». Эта книга более двух тысяч лет служила учебником геометрии во всем мире. Евклид – автор первого дошедшего до нас строгого логического построения геометрии. В нем изложение настолько безупречно для своего времени, что в течение двух тысяч лет с момента появления его труда “Начал” оно было единственным руководством для изучающих геометрию. “Начала” состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении. Каждая книга “Начал” начинается определением понятий, которые встречаются впервые. Так, например, первой книге предпосланы 23 определения. В частности, Определение 1. Точка есть то, что не имеет частей. Определение 2. Линия есть длины без ширины Определение 3. Границы линии суть точки. Вслед за определениями Евклид приводит постулаты и аксиомы, то есть утверждения, принимаемые без доказательства. Постулаты: I. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию. II . И чтобы каждую прямую можно было неопределенно продолжить. III. И чтобы из любого центра можно было описать окружность любым радиусом. IV. И чтобы все прямые углы были равны. V. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние внутренние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых. Аксиомы: I. Равные порознь третьему равны между собой. II. И если к ним прибавим равные, то получим равные. III. И если от равных отнимем равные, то получим равные. IV. И если к неравным прибавим равные, то получим неравные. V. И если удвоим равные, то получим равные. VI. И половины равных равны между собой. VII. И совмещающиеся равны. VIII. И целое больше части. IX. И две прямые не могут заключать пространства. Иногда IV и V постулаты относят к числу аксиом. Поэтому пятый постулат иногда называют XI аксиомой. По какому принципу одни утверждения относятся к постулатам, а другие к аксиомам, неизвестно. Никто не сомневался в истинности постулатов Евклида, что касается и V постулата. Между тем уже с древности именно постулат о параллельных привлек к себе особое внимание ряда геометров, считавших неестественным помещение его среди постулатов. Вероятно, это было связано с относительно меньшей очевидностью и наглядностью V постулата: в неявном виде он предполагает достижимость любых, как угодно далеких частей плоскости, выражая свойство, которое обнаруживается только при бесконечном продолжении прямых. История создания новой геометрии Первым неевклидовым геометром, вероятно, можно считать самого Евклида (рис.1). Его нежелание использовать «не самоочевидный» пятый постулат следует хотя бы из того, что свои первые двадцать восемь предложений Евклид доказывает, не прибегая к этому постулату. С первого века до н.э. до 1820 года математики пытались вывести пятый постулат из остальных, но преуспели лишь в замене его различными эквивалентными допущениями, такими, как «две параллельные линии всюду равно удалены друг от друга» или «любые три точки, не расположенные на одной прямой, принадлежат окружности».  (рис.1) Лобачевский в работе «О началах геометрии» (1829 год), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий. Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи (рис.2), а Карл Фридрих Гаусс (рис.3) пришёл к таким выводам ещё раньше.   (рис.2) (рис.3) Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Сохранились студенческие записи лекций Лобачевского (от 1817 года), где им делалась попытка доказать пятый постулат Евклида, но в рукописи учебника «Геометрия» (1823 год) он уже отказался от этой попытки. В «Обозрениях преподавания чистой математики» за 1822 и 1824 годы Лобачевский указал на «до сих пор непобедимую» трудность проблемы параллелизма и на необходимость принимать в геометрии в качестве исходных понятия, непосредственно приобретаемые из природы. 23 февраля 1826 года гениальный математик читает свой доклад о неевклидовой геометрии ничего не понимающей, скучающей, равнодушной аудитории. Комиссия, ничего не понявшая, не дает никакого отзыва. Работа не была напечатана. И только в 1829 году были опубликованы мемуары «О началах геометрии» - первая работа по неевклидовой геометрии. Работу не поняли. Из Академии наук пришел уничтожающий отзыв, появляются статьи, где Лобачевского называют провинциальным шарлатаном, невежественным самодовольным ничтожеством. Авторы этих отзывов опирались на то, что все, что изложено господином Лобачевским (рис.4) в своих трудах не имеет места в природе и, поэтому, совершенно для разума непонятно и абсурдно. Лобачевского никто не поддержал, но у него хватило мужества отстаивать свои идеи до конца.  (рис.4) Не найдя понимания на Родине, Лобачевский попытался найти единомышленников за рубежом. В 1837 году статья Лобачевского «Воображаемая геометрия» на французском языке (Géométrieimaginaire) появилась в авторитетном берлинском журнале Крелле, а в 1840 году Лобачевский опубликовал на немецком языке небольшую книгу «Геометрические исследования по теории параллельных», где содержится чёткое и систематическое изложение его основных идей. Два экземпляра получил Карл Фридрих Гаусс, «король математиков» той поры. Как много позже выяснилось, Гаусс и сам тайком развивал неевклидову геометрию, однако так и не решился опубликовать что-либо на эту тему. Пятый постулат Евклида стал своего рода толчком к созданию другой геометрии, или продолжением геометрии Евклида. Одновременно учёные многих стран пришли к одним и тем же выводам. Однако одних учёных не поняли, как Лобачевского, другие боялись опубликовать свои труды. Создателями неевклидовой геометрии стали такие яркие учёные, как сам Евклид, Гаусс, Бойяи, Лобачевский. У некоторых учёных открытия в неевклидовой геометрии происходили одновременно, независимо друг от друга. Неевклидова геометрия Лобачевский считал аксиому параллельности Евклида произвольным ограничением. С его точки зрения, это требование слишком жёсткое, ограничивающее возможности теории, описывающей свойства пространства, и поэтому в создании неевклидовой геометрии он использовал плоскостные постулаты Евклида как частный, предельный случай и отказался от V постулата, приняв независимость аксиомы о параллельных прямых Евклида от остальных аксиом. Вместо V постулата он принимает противоположное предложение: на плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную. Вместе с этим предложением Лобачевский принимает остальные аксиомы Евклидовой геометрии и на этом основании строит новую геометрию. Получившаяся геометрия логически стройная, нигде противоречий не встречается. Лобачевский называет ее «воображаемой». Через точку С, лежащую вне прямой АВ, можно, предположил Лобачевский, провести хотя бы две прямые а и b, которые не пересекутся с прямой АВ (рис.5). Точно так же не пересекают прямую АВ и прямые m, n, p, проходящие через точку С. 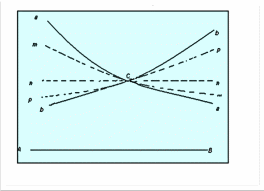 (рис.5) Сумма углов треугольника в «воображаемой геометрии» всегда меньше180о (рис.6). 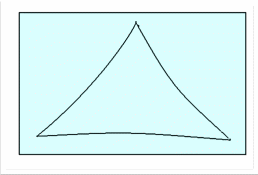 (рис.6) В плоскости Лобачевского не существует никакого подобия. Ведь все теоремы о подобии выводятся только с помощью аксиомы Евклида о параллельности. Н.И. Лобачевский установил, что на предельной поверхности, называемой орисферой, внутренняя геометрия является евклидовой. Разработанная Лобачевским новая геометрия не включает в себя евклидову геометрию, однако евклидова геометрия может быть из неё получена предельным переходом (при стремлении кривизны пространства к нулю). В самой геометрии Лобачевского кривизна отрицательна. Уже в первой публикации Лобачевский детально разработал тригонометрию неевклидова пространства, дифференциальную геометрию (включая вычисление длин, площадей и объёмов) и смежные аналитические вопросы. В геометрии Н.И. Лобачевского используются основные понятия Евклида: перпендикуляры, осевые симметрии и повороты. В ней сохраняются свойства равнобедренного треугольника, известные признаки равенства треугольников и другие элементы «абсолютной геометрии». В пространстве Лобачевского были выделены криволинейные геометрические образы, подчинённые геометрии Евклида. Этот замечательный результат Лобачевский использовал для вывода тригонометрических соотношений между элементами прямолинейных треугольников в его пространстве. Но итоговые соотношения гораздо сложнее евклидовых. Эти соотношения имеют не только тригонометрические функции углов, не просто длины сторон, а некоторые функции от них. Сделав свое знаменитое открытие, Н. И. Лобачевский не опроверг евклидову геометрию, а лишь раздвинул границы науки, существовавшей в Древнем мире. Любые факты планиметрии Лобачевского не противоречат геометрии Евклида. Однако созданная геометрия существенно отличается от прежней. Лобачевский, очевидно, хотел подчеркнуть противоречие V постулату: на плоскости через точку, лежащую вне данной прямой, проходит более одной прямой, не пересекающей данную. И тем самым заменил евклидов постулат более общей аксиомой параллельности и сохранил все рассуждения геометрии Евклида. Пятый пустулат Сам Евклид формулировал его так: «Если прямая пересекает две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где сумма углов меньше двух прямых». Другие формулировки гораздо проще, например: «через точку вне прямой можно провести одну и только одну прямую, параллельную данной». 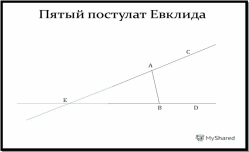 Конечно, ещё сам Евклид пытался вывести этот сложный постулат из более простых. После него этой проблемой занимались почти все известные математики, но чаще всего это заканчивалось тем, что постулат выводился только при принятии каких-то дополнительных предположений. У менее удачливых математиков не получалось вообще ничего. Самую известную попытку доказать пятый постулат методом от противного предпринял итальянский монах Джироламо Саккерти в 1733 году. Но отрицание пятого постулата – это и есть главное отличие геометрии Лобачевского от геометрии Евклида. Он, как и другой математик И. Г. Ламберт в 1766 году, вплотную подошел к неевклидовой геометрии, но не нашел её реальной. Гаусс, Больяи, Швейкарт, Тауринус – они все рано или поздно убеждались, что доказать пятый постулат невозможно. Сам Лобачевский говорил об этой проблеме: «Напрасные страданья … в продолжение двух тысяч лет». И именно он смог отвергнуть этот постулат, создав новую геометрию. Гаусс, изучая поверхности, обнаружил, что на поверхностях отрицательной кривизны сумма углов треугольника меньше 180о. Он был в шаге от опровержения пятого постулата. Попыток было много – и именно недоказуемость этого предположения привела к открытию неевклидовой геометрии. Отзывы и доказательства В последние годы жизни Лобачевский безуспешно пытался доказать непротиворечивость своей геометрии. Чтобы получить такое доказательство, надо было построить модель геометрии. В 1868 году (через 12 лет после смерти Лобачевского) итальянский ученый Э. Бельтрами исследовал вогнутую поверхность называемую псевдосферой и доказал, что на этой поверхности действует геометрия Лобачевского (рис.7). В 1868г. Итальянский математик Э. Бельтрами исследовал вогнутую поверхность, называемую псевдосферой, и доказал, что на этой поверхности действует геометрия Лобачевского.  (рис. 7) А через 2 года немецкий математик Клейн предлагает другую модель плоскости Лобачевского (рис.8). Клейн берет некоторый круг. «Плоскостью» Клейн называет внутренность круга. Далее, каждую хорду круга (без концов, поскольку берутся только внутренние точки круга) Клейн считает «прямой». Теперь в этой «плоскости» можно рассматривать отрезки, треугольники и т. д. Две фигуры называются «равными», если одна из них может быть переведена в другую некоторым движением. Тем самым введены все понятия, упоминаемые в аксиомах геометрии, и можно проводить проверку выполнения аксиом в этой модели. Например, очевидно, что через любые две точки А, В проходит единственная «прямая». Можно проследить также, что через точку А, не принадлежащую «прямой» а, проходит бесконечно много «прямых», не пересекающих а. Дальнейшая проверка показывает, что в модели Клейна выполняются и все остальные аксиомы геометрии Лобачевского. 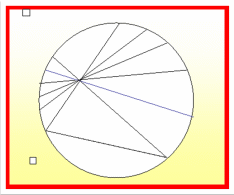 (рис.8) Еще одна модель геометрии Лобачевского была предложена французским математиком А. Пуанкаре (1854-1912). Он также рассматривает внутренность некоторого круга. «Прямыми» он считает дуги окружностей, которые в точках пересечения с границей круга касаются радиусов (рис.9). 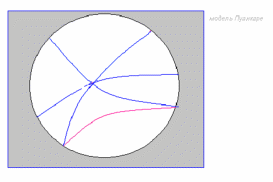 (рис.9) В конце прошлого века в работах Пуанкаре и Клейна была установлена прямая связь геометрии Лобачевского с теорией функций комплексной переменной и с теорией чисел (точнее, арифметикой неопределенных квадратичных форм). С тех пор аппарат геометрии Лобачевского стал неотъемлемым компонентом этих разделов математики. В последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий (рис.10). Десятки работ ежегодно публикуются в этой области. В связи с этим можно говорить о конце романтического периода в истории геометрии Лобачевского, когда основное внимание исследователей было обращено на ее осмысление с точки зрения оснований геометрии вообще. Современные исследования все больше требуют делового владения геометрией Лобачевского.  (рис. 10) Важное замечание, касающееся чертежей, изображающих поведение прямых на плоскости Лобачевского. Как показывают опыты, наше физическое пространство по свойствам или евклидово, или очень мало от него отличается. Оперируя с чертежом, вынуждены ограничиться его малым размером, а отклонение от евклидовости, если оно существует, будет наблюдаться только при очень больших протяжениях. Поэтому для наглядности обычно принято изображать прямые, слегка их искривляя, чтобы отчётливее выразить характер их сближения или расхождения на плоскости Лобачевского. Однако Лобачевский такие вольности себе не разрешал. Сколько времени нужно было учёным, чтобы проверить на различных моделях: псевдосфере Клейна, модель Пуанкаре, трёхмерные многообразия математика Тёрстона, что геометрия Лобачевского действует? Какие сомнения возникали у самого Лобачевского в правильности его идей?! Но именно элементы геометрии Лобачевского стали основой таких разделов математики, как теория чисел и теория функций комплексной переменной и многих других. Значение Неевклидовой геометрии Новая геометрия явилась чистым порождением разума, отделившейся от окружающей действительности. Поэтому Лобачевский назвал ее «воображаемой». Появление неевклидовой геометрии было важным шагом в превращении математики в науку о логически мыслимых формах и отношениях. Этот процесс шел по всему фронту не только в геометрии, но и в алгебре. Появились теория множеств, математическая логика. В геометрии вскоре за геометрией Лобачевского появилась многомерная евклидова геометрия. Лобачевский был назван «Коперником геометрии», но его можно назвать и Колумбом науки, открывшим новую ее область, за которой следовал материк новой геометрии и вообще новой математики. Тот путь, на который впервые стал Лобачевский, в значительной степени определил лицо современной науки. Открытие новой геометрии стало началом многочисленных исследований выдающихся математиков 19 века. Геометрия послужила толчком к развитию науки, а значит и пониманию мира, который на окружает. А в начале 20-говека было обнаружено, что геометрия Лобачевского совершенно необходима в современной физике. Например, в теории относительности Эйнштейна, в расчетах современных синхрофазотронов, в космонавтике. Заключение Создателями неевклидовой геометрии стали такие яркие учёные, как сам Евклид, Гаусс, Бойяи, Лобачевский. Евклид делал попытки доказать пятый постулат, но у него не получалось. У некоторых учёных открытия в неевклидовой геометрии происходили одновременно, независимо друг от друга. Н. И. Лобачевский раздвинул границы науки, существовавшей на тот момент. Любые факты планиметрии Лобачевского не противоречат геометрии Евклида. Однако созданная геометрия существенно отличается от прежней. Лобачевский, очевидно, хотел подчеркнуть противоречие V постулату: на плоскости через точку, лежащую вне данной прямой, проходит более одной прямой, не пересекающей данную. И тем самым заменил евклидов постулат более общей аксиомой параллельности и сохранил все рассуждения геометрии Евклида. Много времени понадобилось учёным, чтобы проверить на различных моделях: псевдосфере Клейна, модель Пуанкаре, трёхмерные многообразия математика Тёрстона, что геометрия Лобачевского действует? Какие сомнения возникали у самого Лобачевского в правильности его идей?! Но именно элементы геометрии Лобачевского стали основой таких разделов математики, как теория чисел и теория функций комплексной переменной и многих других. Лобачевский был назван «Коперником геометрии», но его можно назвать и Колумбом науки, открывшим новую ее область, за которой следовал материк новой геометрии и вообще новой математики. Тот путь, на который впервые стал Лобачевский, в значительной степени определил лицо современной науки. Открытие новой геометрии стало началом многочисленных исследований выдающихся математиков 19 века. Геометрия послужила толчком к развитию науки, а значит и пониманию мира, который на окружает. А в начале 20-говека было обнаружено, что геометрия Лобачевского совершенно необходима в современной физике. Например, в теории относительности Эйнштейна, в расчетах современных синхрофазотронов, в космонавтике. Список использованных источников Лаптев Б.Л. Н.И.Лобачевский и его геометрия. Пособие для учащихся. М., «Просвещение», 1976. Шербаков Р.Н., Пичурин Л.Ф. от проективной геометрии – к неевклидовой (вокруг абсолюта): Кн. Для внеклассного чтения. IX, X кл. – М.: Просвещение, 1979. – 158с., ил.- (Мир знаний) Погорелов А.В. Геометрия: Учеб. Для 7-9 кл. общеобразоват. учреждений/ А.В. Погорелов.-5-е изд. – М.: Просвещение, 2010.-224 с. uztest.ru/abstracts/?idabstract=336056 |
