Математика. Реферат Производная и ее приложения ученик 11А класса Новиков А. Проверила Шекера Г. В. г. Хабаровск
 Скачать 1.6 Mb.
|
9.4.Разложение выражения на множители с помощью производной.Задача 1. Разложить на множители выражение:  (1)Решение: Считая  переменной, а  и  посто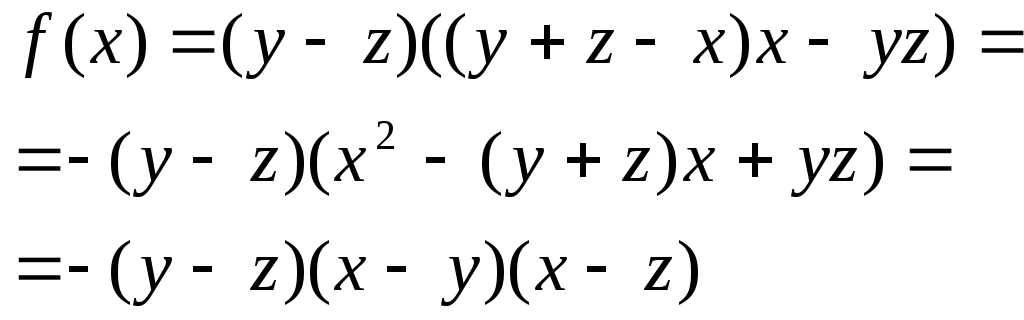янными фиксированными (параметрами) и обозначая заданное выражение через  , будем иметь: Поэтому  (2)где  - постоянная, т.е. в данном случае - выражение, зависящее от параметров и . Для нахождения в равенстве  положим  тогда  .Получим  Задача 2. Разложить на множители выражение:  (3)Решение: Поскольку переменная входит в данное выражение в наименьшей степени, рассмотрим его, как функцию  и будем иметь:  получим: Таким образом, исходное выражение (3) равно  Задача 3. Разложить на множители выражение:  Решение: Обозначив данное выражение через и считая и постоянными, получим: откуда  , где зависит только от и . Положив в этом тождестве  , получим  и  Для разложения на множители второго множителя используем тот же приём, но в качестве переменной рассмотрим , поскол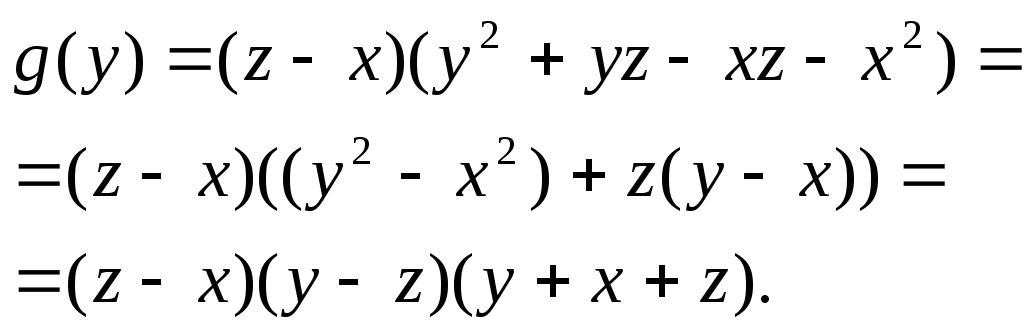ьку эта переменная входит в меньшей степени, чем . Обозначая его через  и считая и постоянными, будем иметь: отсюда:    Таким образом исходное выражение (4) равно  9.5. Применение производной в вопросах существования корней уравнений.С помощью производной можно определить сколько решений имеет уравнение. Основную роль здесь играют исследование функций на монотонность, нахождение её экстремальных значений. Кроме того, используется свойство монотонных функций: Задача 1. Если функция  возрастает или убывает на некотором промежутке, то на этом промежутке уравнение  имеет не более одного корня. (1)Решение: Область определения данного уравнения - промежуток  определение на этом промежутке функцию , положив Тогда, на      ,и таким образом функция - возрастающая, так что данное уравнение (1) не может иметь более одного решения.Задача 2. При каких значениях  имеет решения уравнение (2)Решение: область определения уравнения - отрезок  , рассмотрим функцию , положив  Тогда на открытом промежутке   , так что  - единственная критическая точка функции , являющаяся, очевидно, точкой максимума. Поскольку   то примет наибольшее значение при  , а наименьшее значение - при  . Так как функция непрерывна, то её область значений представляет собой отрезок  , между её наименьшим и наибольшим значением. Другими словами, исходное уравнение (2) имеет решения при  .Заключение Настоящая работа даёт учащимся новый подход к многим преобразованиям в математике, которые стандартным путём трудно разрешимы или разрешимы, но громоздкими способами. Рассмотренные подходы нестандартного характера для учащихся покажутся новыми и необыкновенными, что расширит их кругозор и повысит интерес к производной. Итак, геометрический смысл производной: производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0. Физический смысл производной: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0 Экономический смысл производной: производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Производная находит широкое приложение в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени; для нахождения наибольших и наименьших величин. Производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул. Наиболее актуально использование производной в предельном анализе, то есть при исследовании предельных величин (предельные издержки, предельная выручка, предельная производительность труда или других факторов производства и т. д.). Производная применяется в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре и геометрии. |