|
|
Математика. Реферат Производная и ее приложения ученик 11А класса Новиков А. Проверила Шекера Г. В. г. Хабаровск
О
–
твет: 50 Ом 9.1. Применение производной к доказательству неравенств.
Одно из простейших применений производной к доказательству неравенств основано на связи между возрастанием и убыванием функции на промежутке и знаком ее производной. С помощью теоремы Лагранжа доказана теорема:
Теорема 1. Если функция 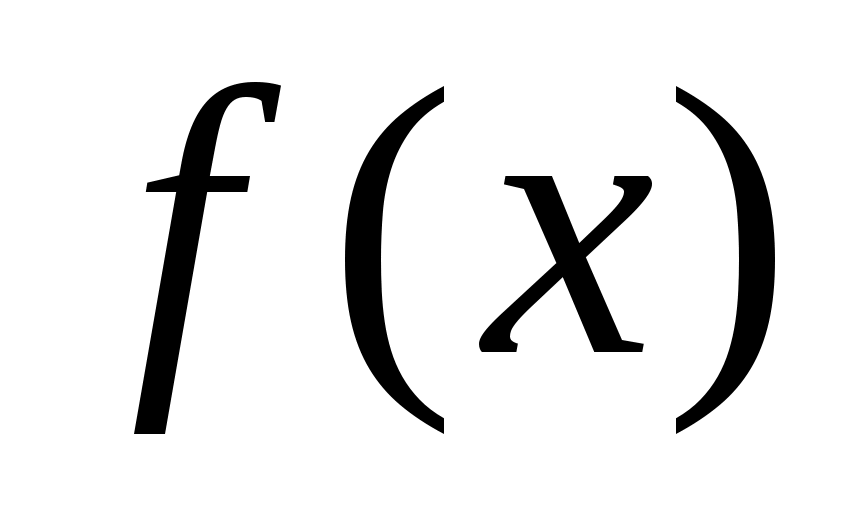 на некотором интервале на некотором интервале 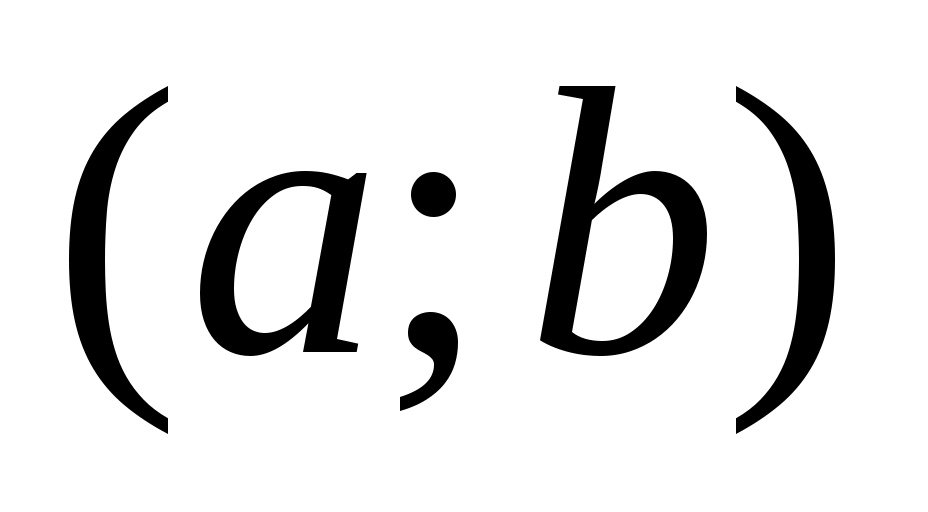 имеет производную имеет производную 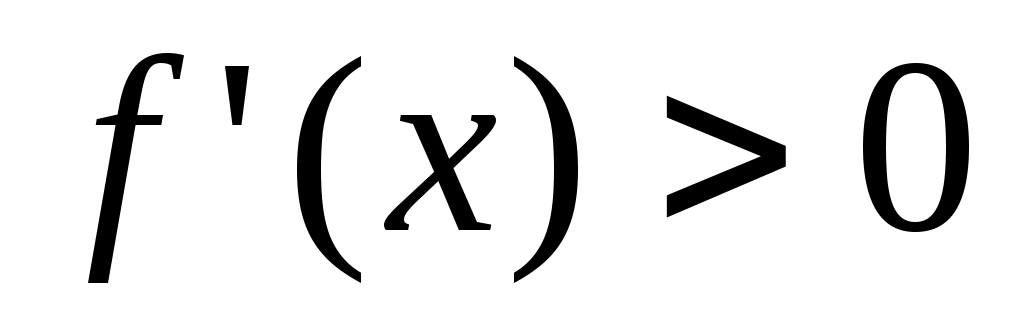 всюду на всюду на 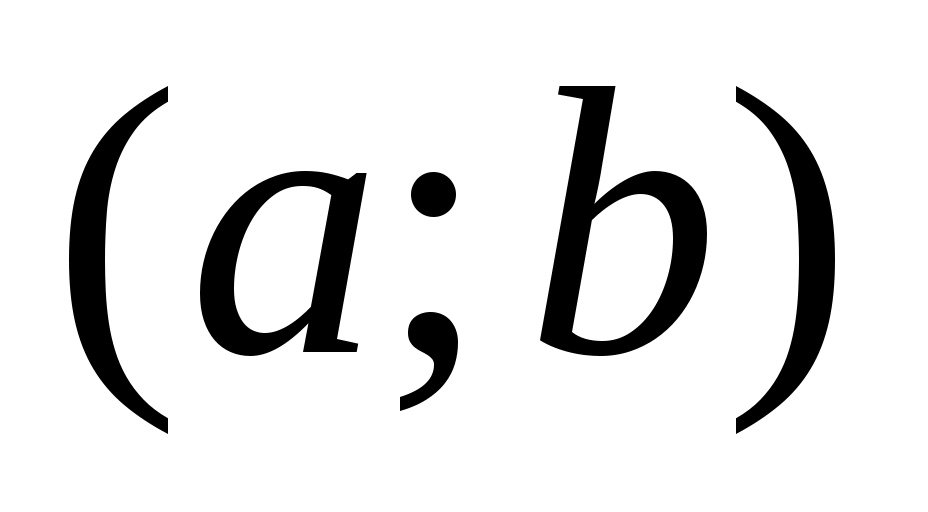 , то , то 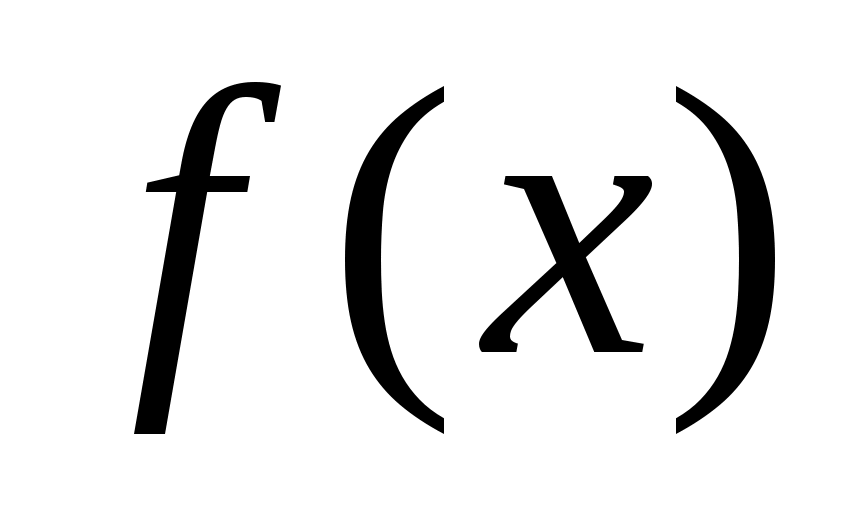 на на 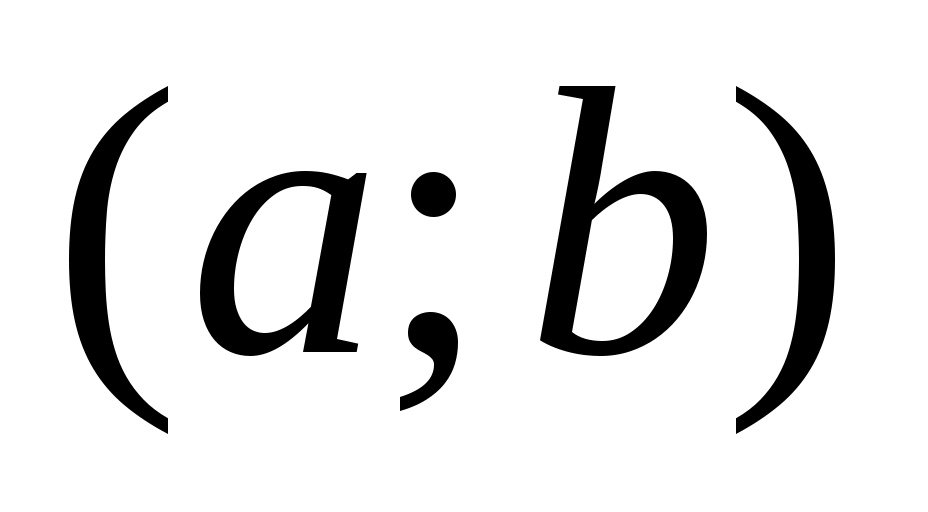 монотонно возрастает; если же монотонно возрастает; если же 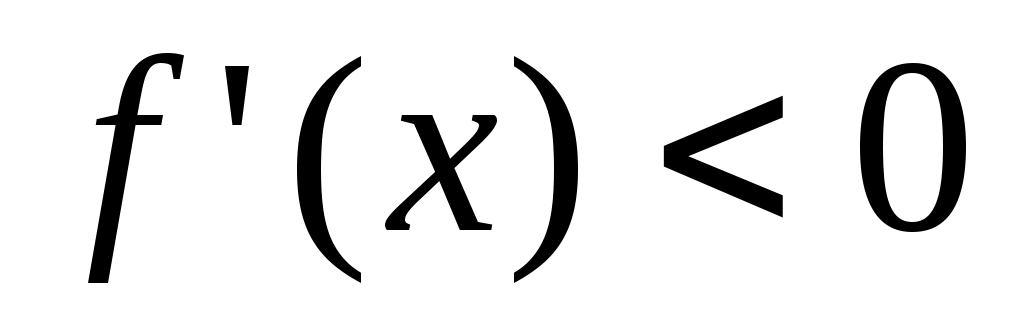 всюду на всюду на 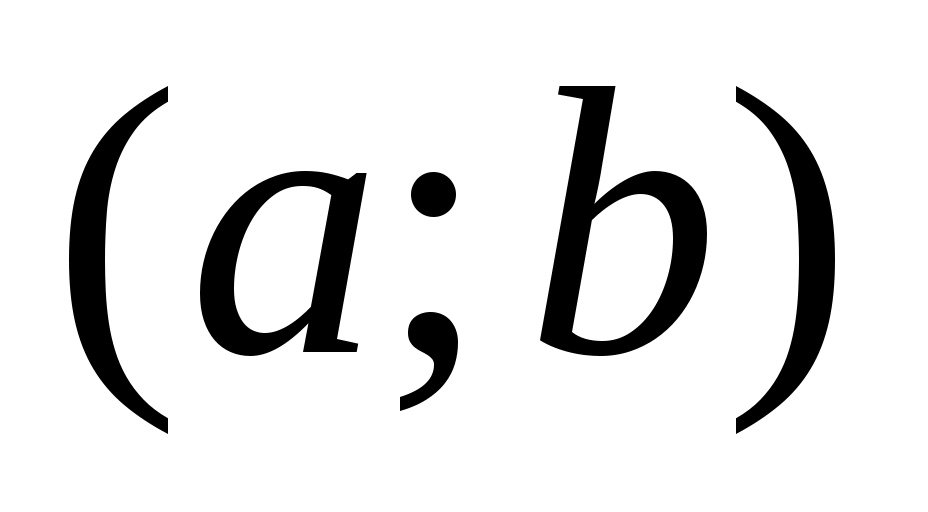 , то , то 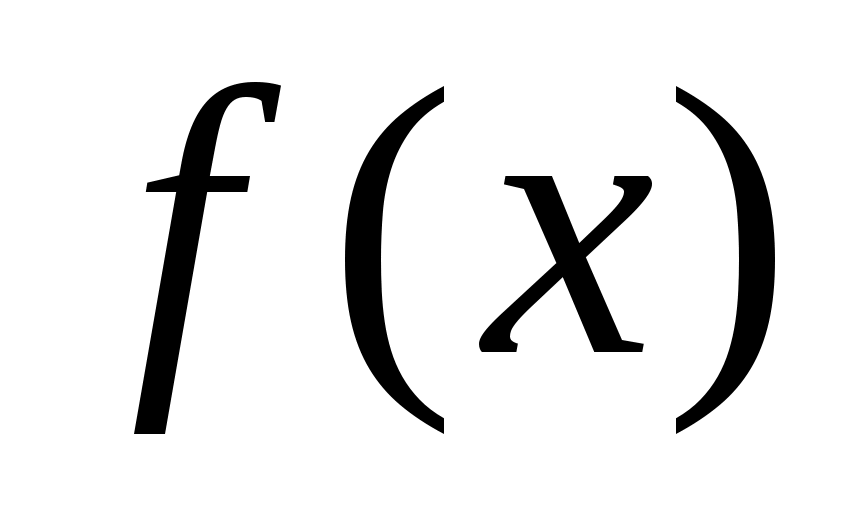 на на 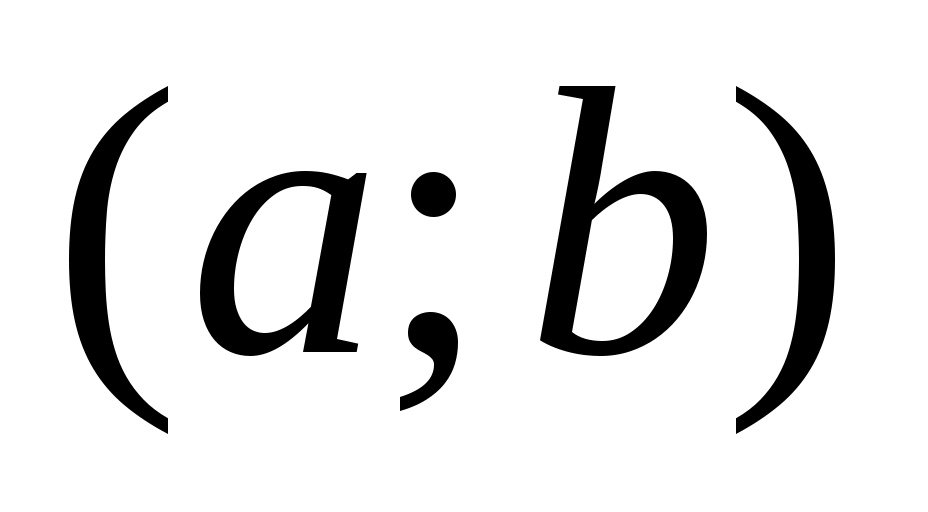 монотонно убывает. монотонно убывает.
Очевидным следствием (и обобщением) этой теоремы является следующая:
Теорема 2. Если на промежутке 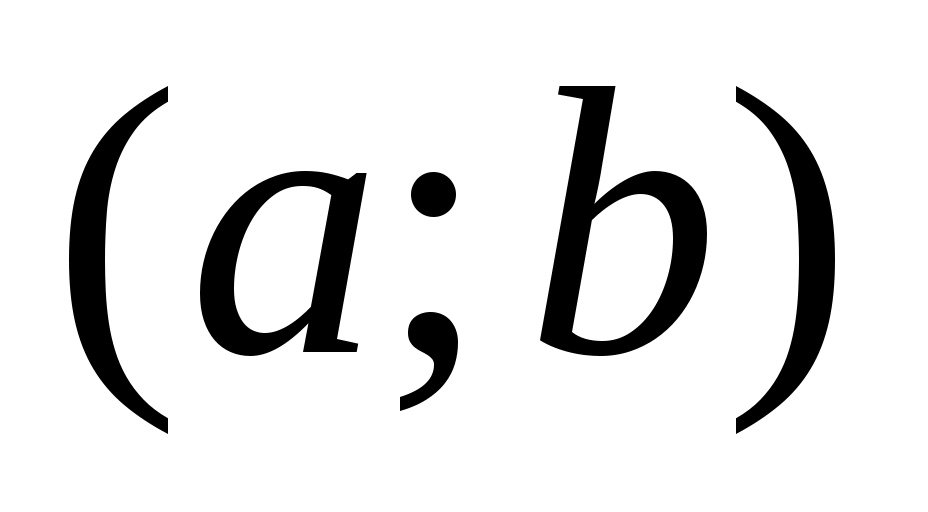 выполняется неравенство выполняется неравенство 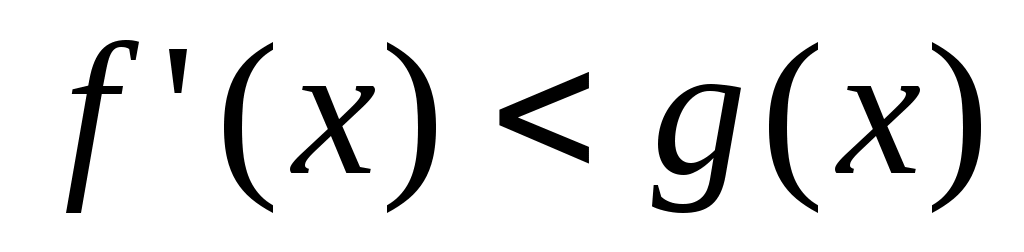 , функция , функция 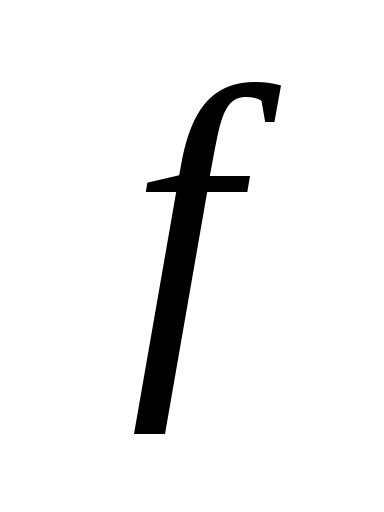 и и 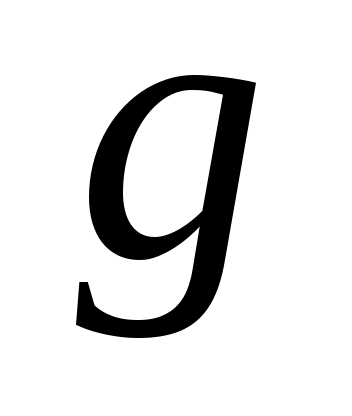 непрерывны в точке непрерывны в точке  и и 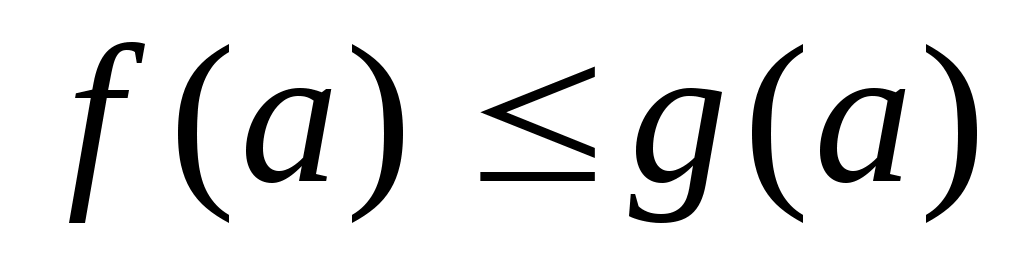 , то на , то на 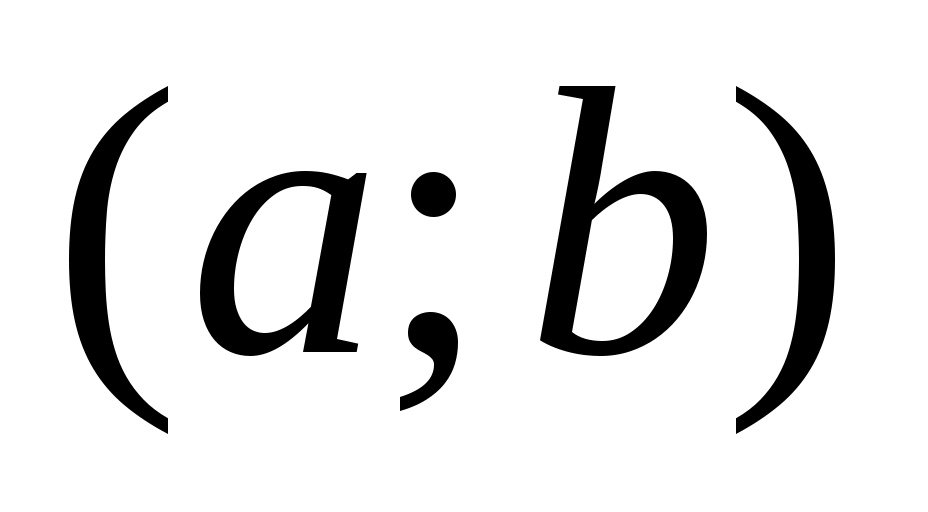 выполняется неравенство выполняется неравенство 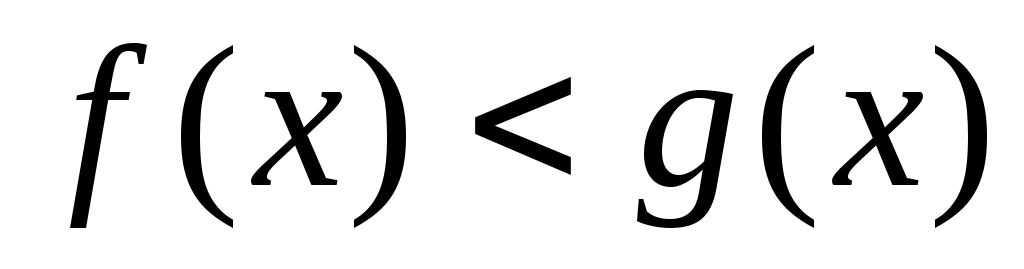 . .
Предлагаю несколько задач на доказательство неравенств с использованием этих теорем.
Задача 1. Пусть 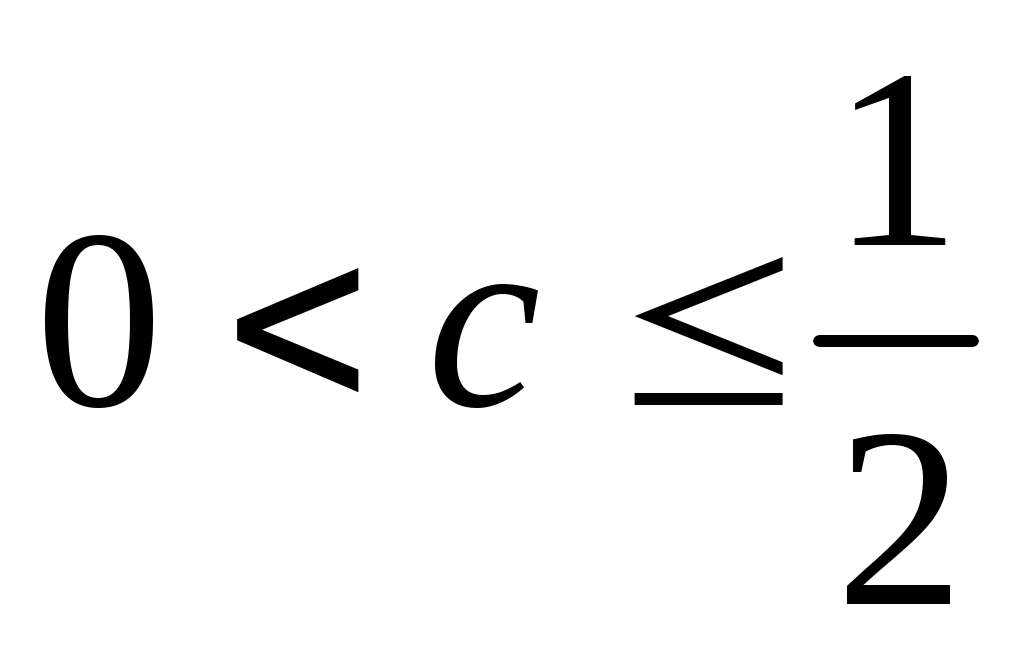 .Докажите истинность неравенства .Докажите истинность неравенства 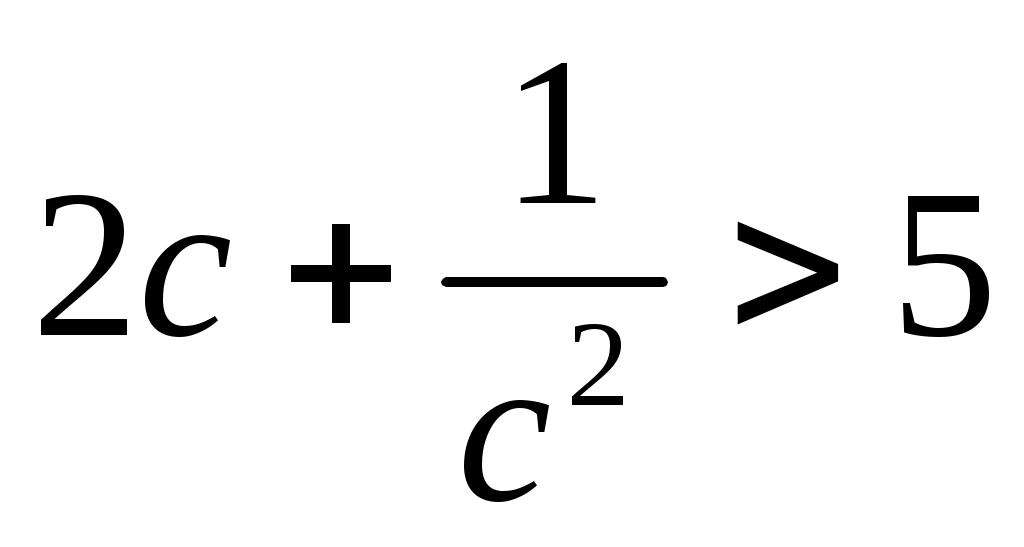 . (1) . (1)
Решение: Рассмотрим на 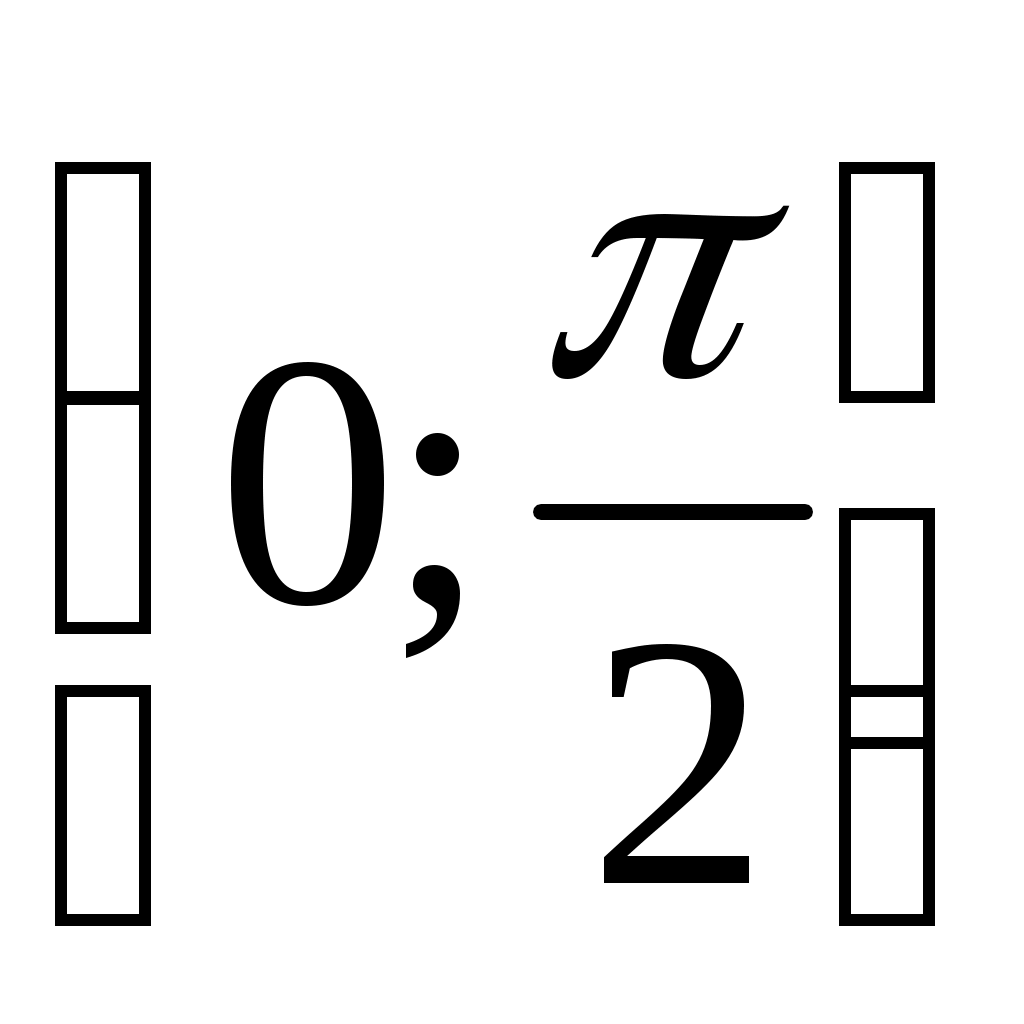 функцию функцию 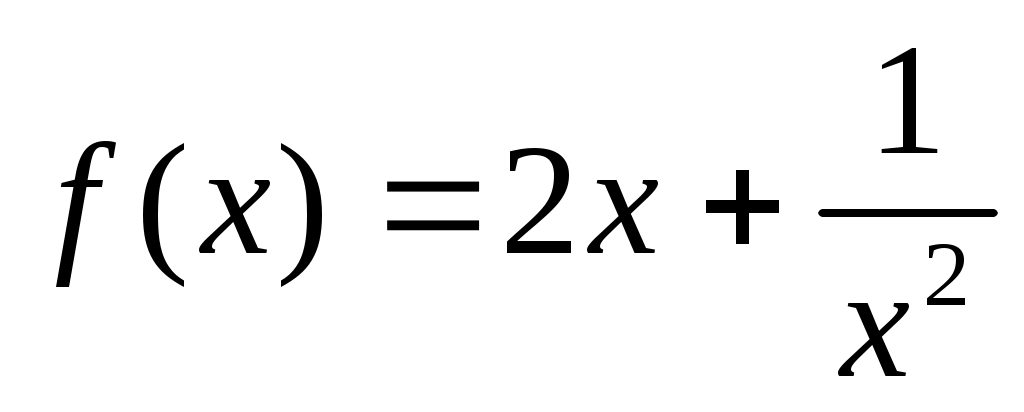 . Найдем ее производную: . Найдем ее производную: 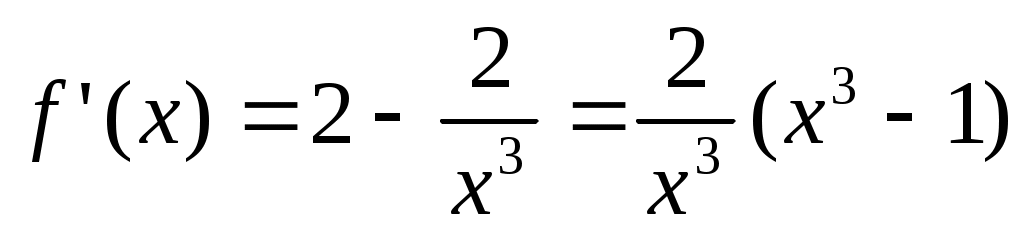 . Видим, что . Видим, что 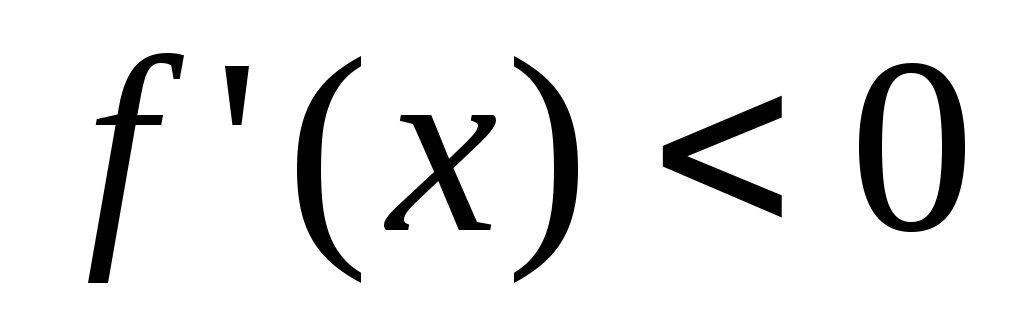 при при 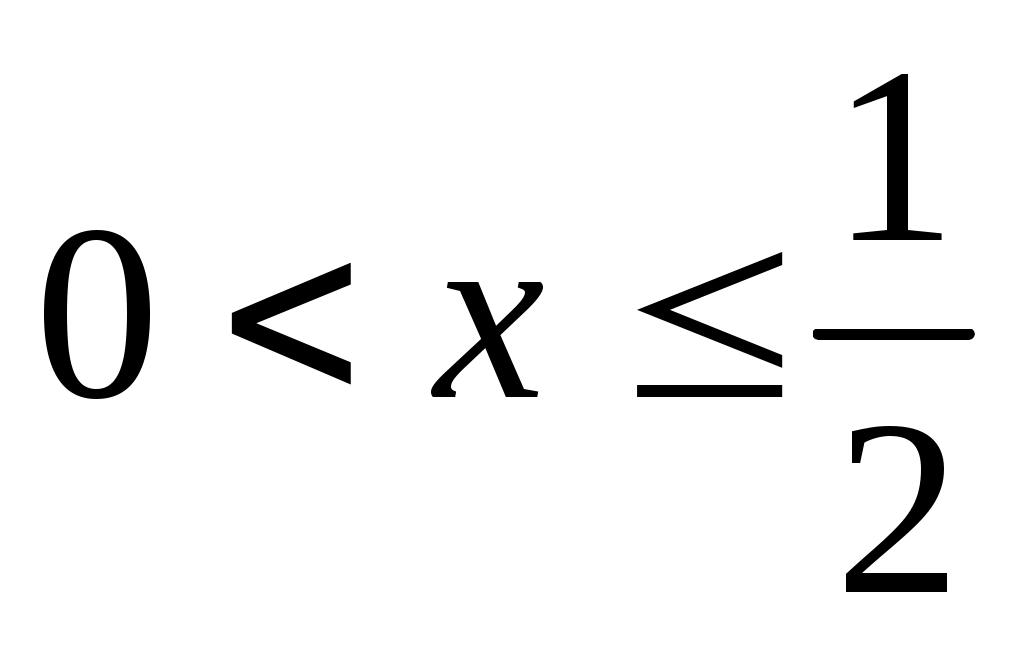 . Следовательно, . Следовательно, 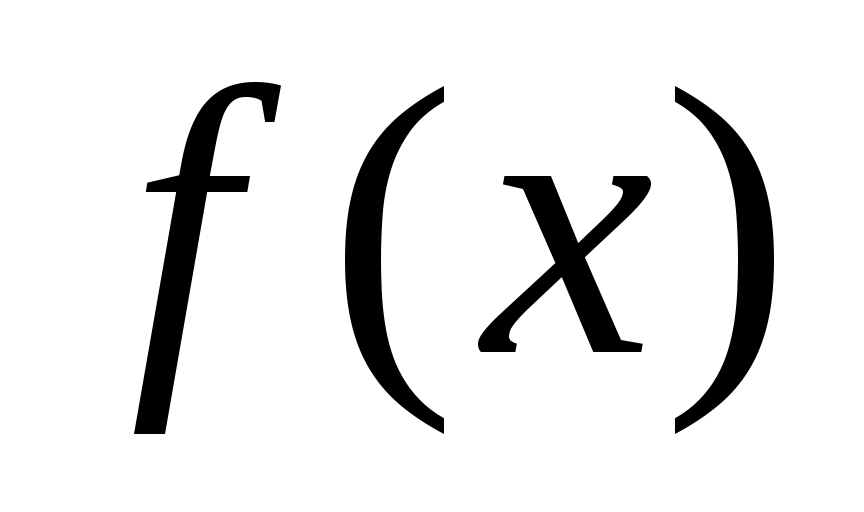 на на 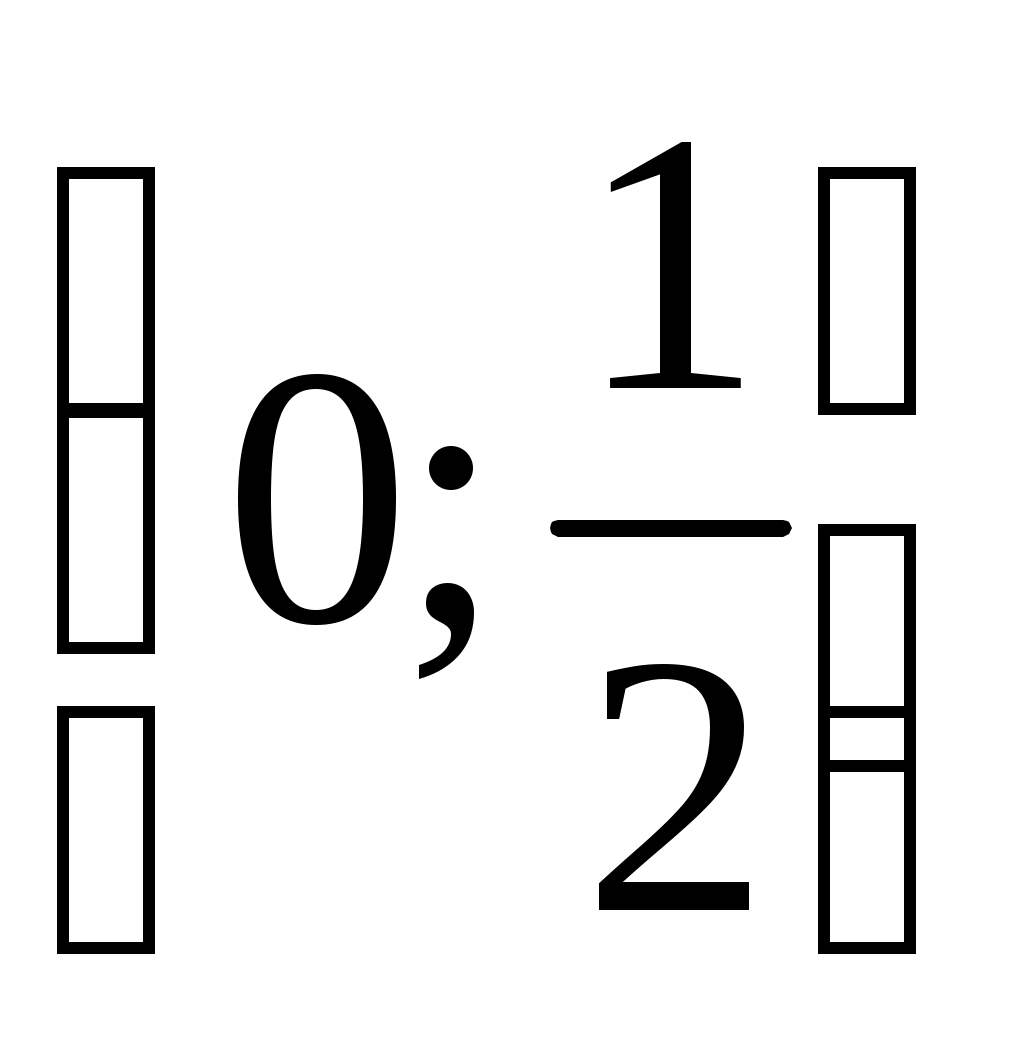 убывает так, что при убывает так, что при 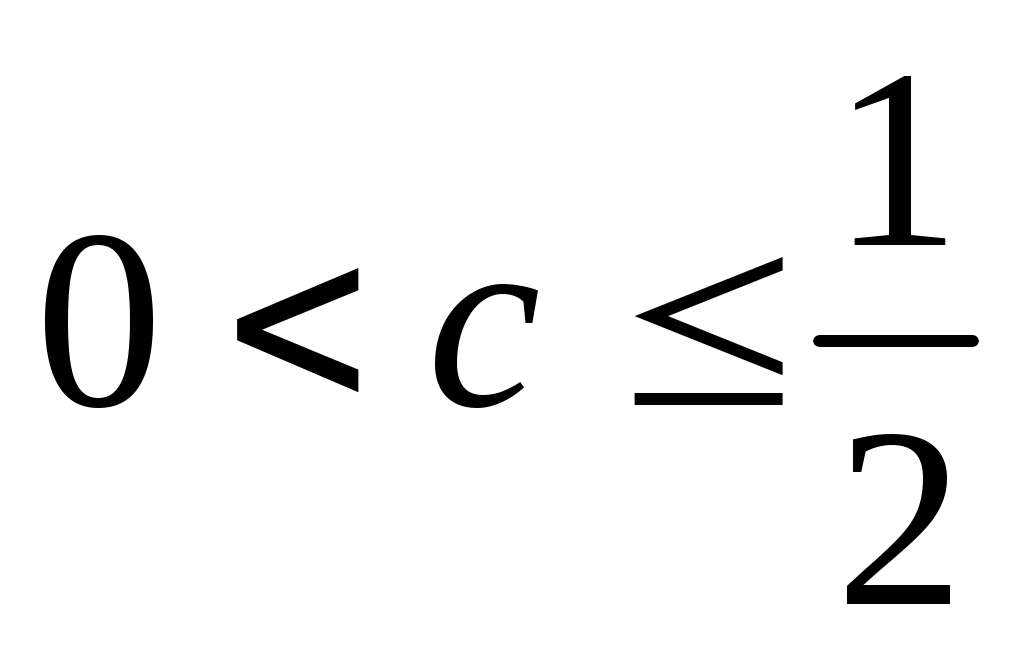 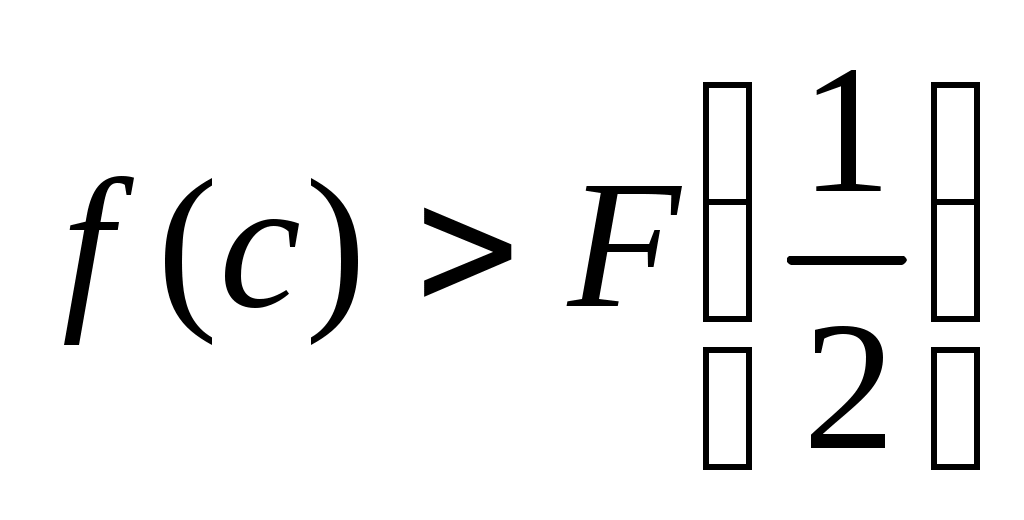 . Но . Но  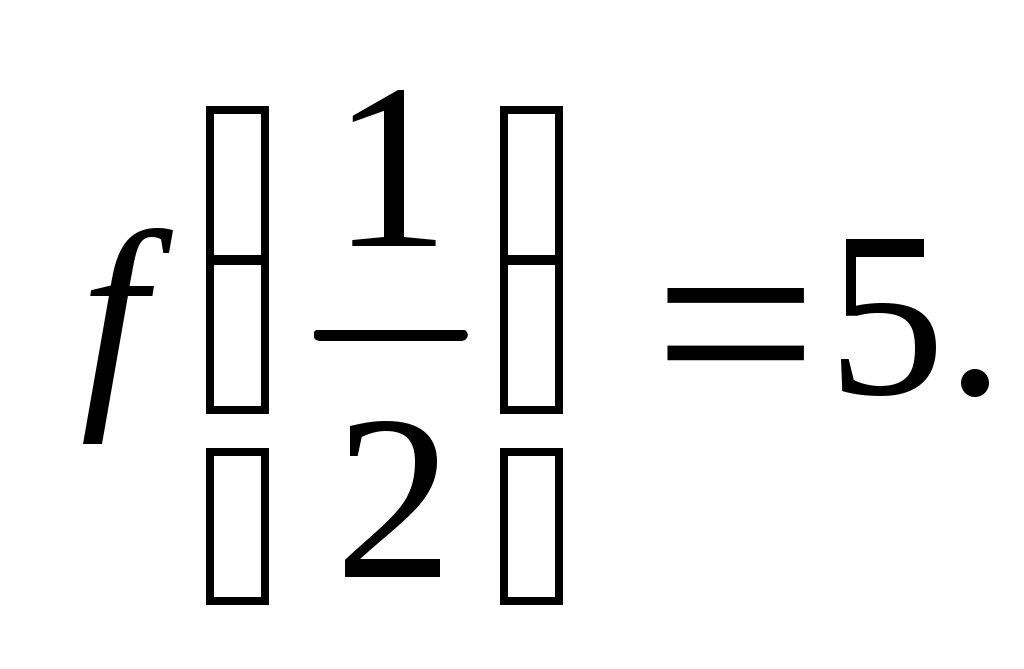 Следовательно неравенство (1) Следовательно неравенство (1) 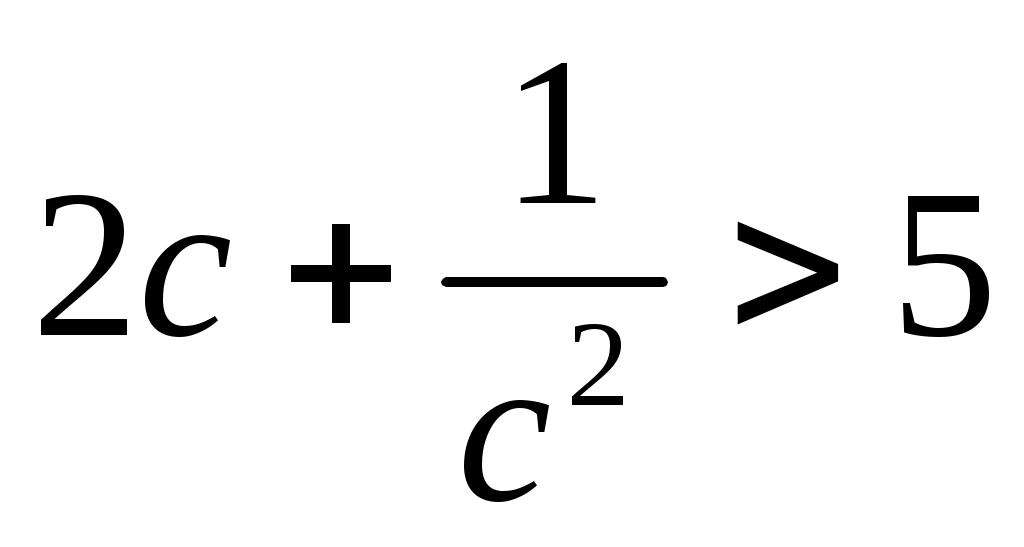 верно. верно.
Задача 2. Пусть 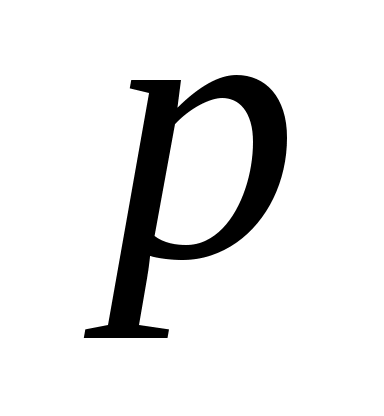 и и 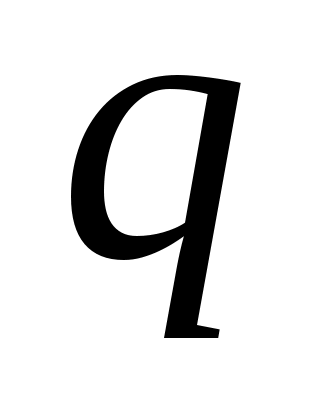 положительные числа, положительные числа, 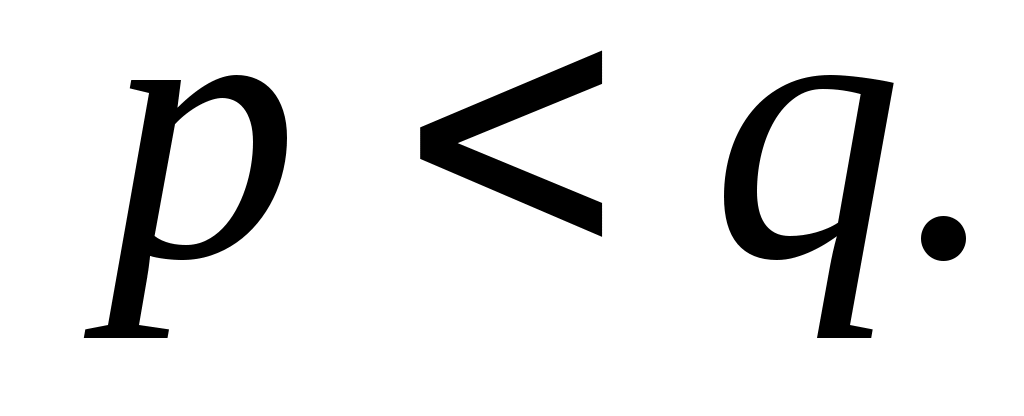 Тогда очевидно, что Тогда очевидно, что 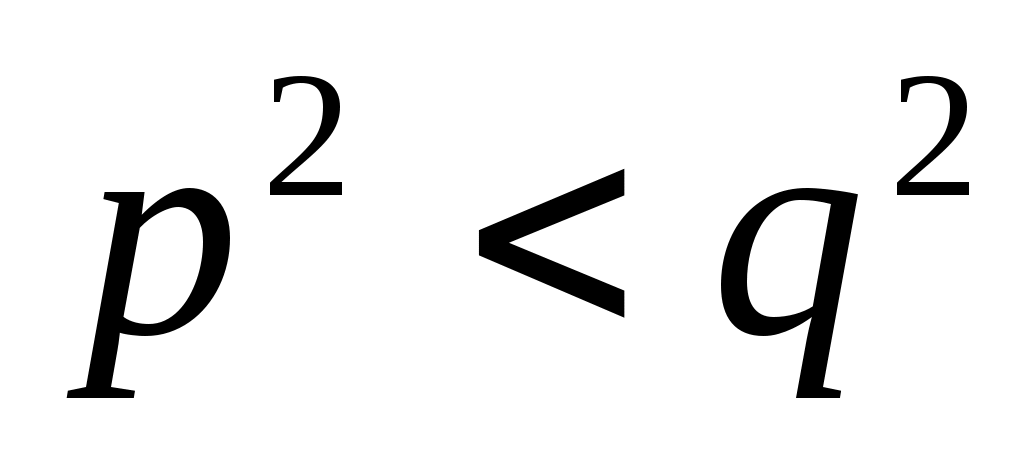 , , 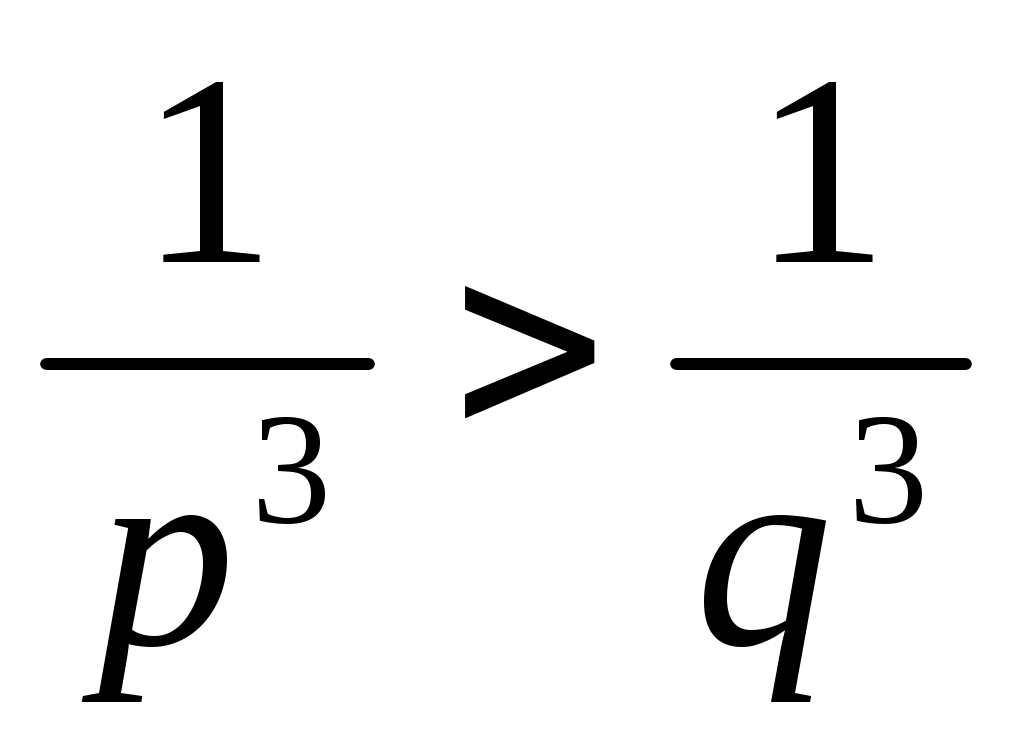 . Можно ли гарантировать, что неравенство . Можно ли гарантировать, что неравенство 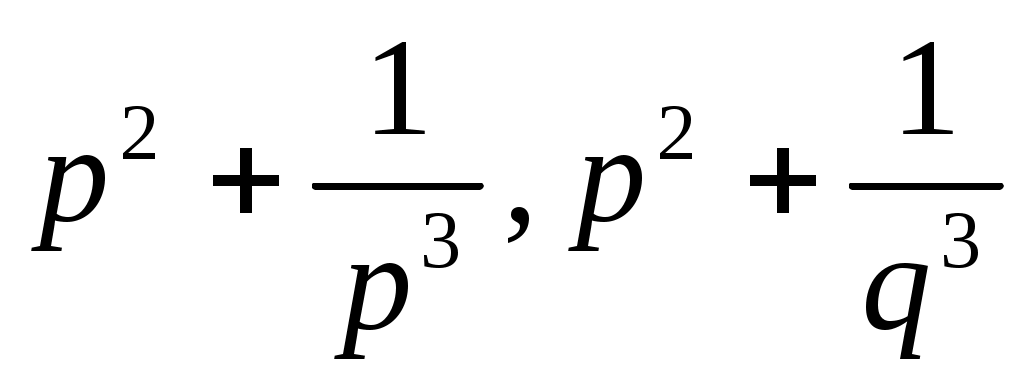 (2) (2)
верно а) при 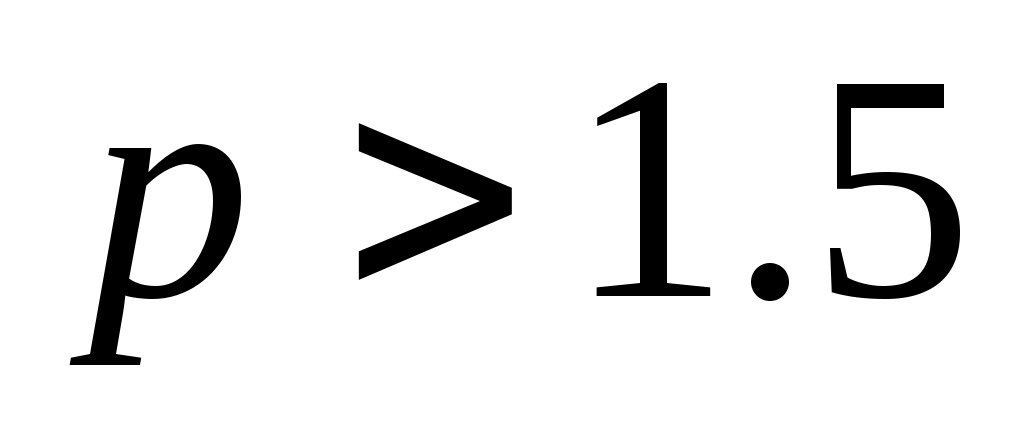 ; б) при ; б) при 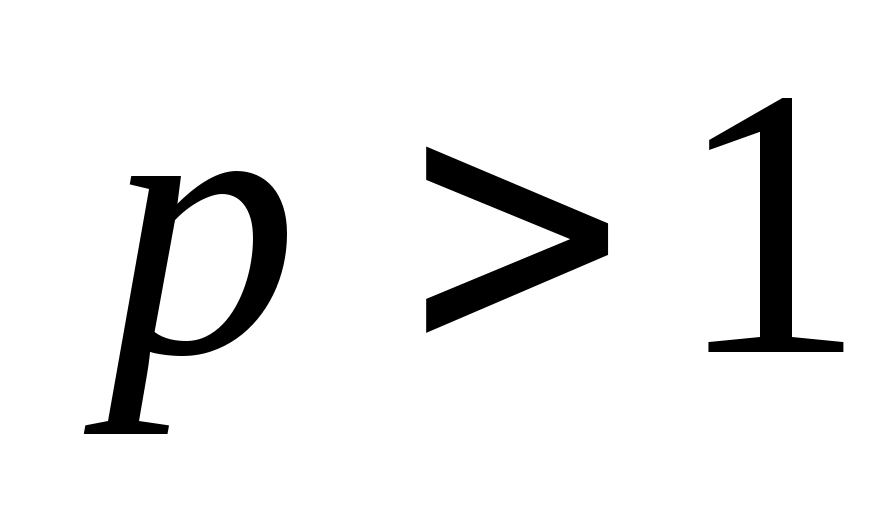 ? ?
Решение: а) Рассмотрим функцию 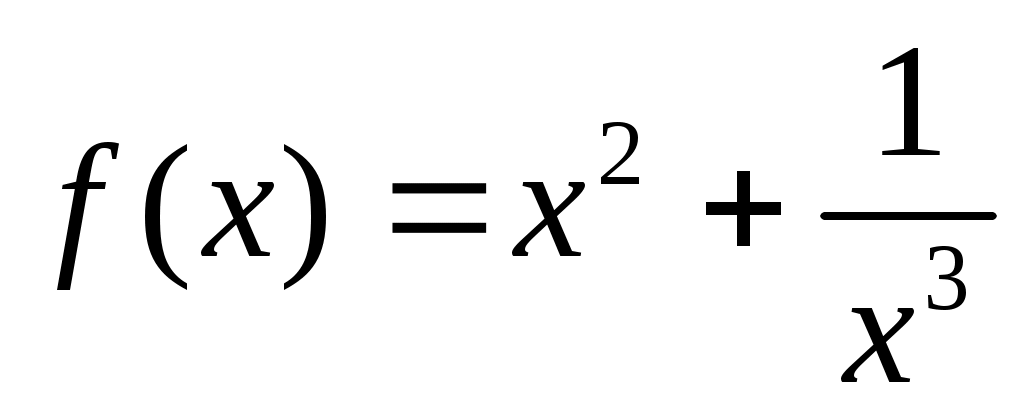 . Имеем: . Имеем: 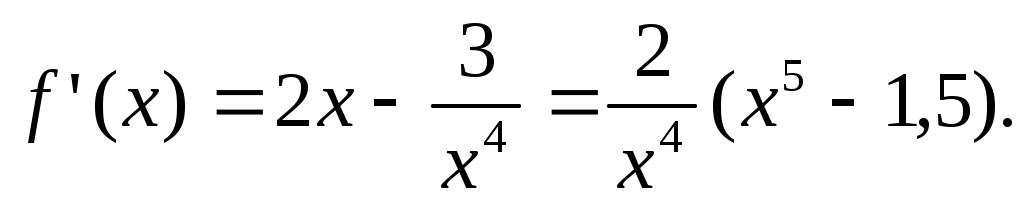
Отсюда видно, что при 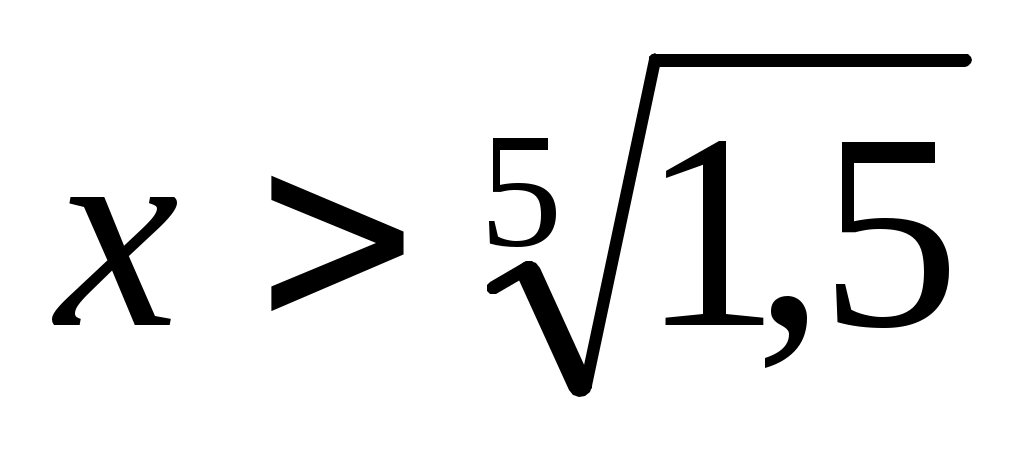 функция функция 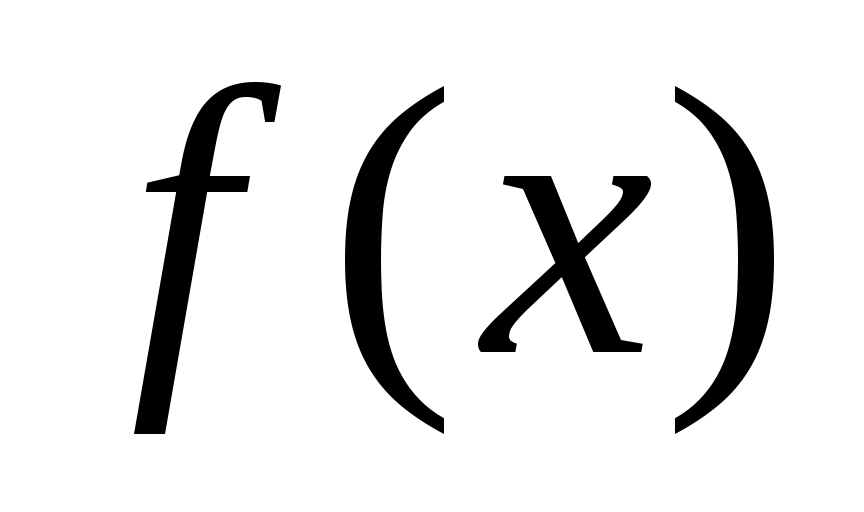 возрастает. В частности, она возрастает на интервале возрастает. В частности, она возрастает на интервале 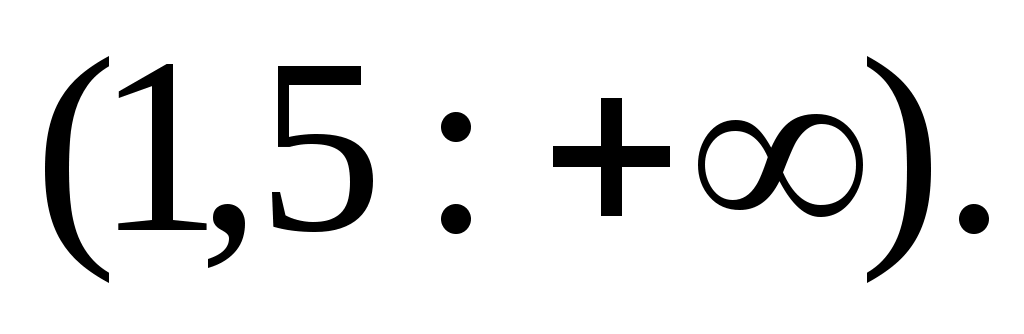 Поэтому при Поэтому при 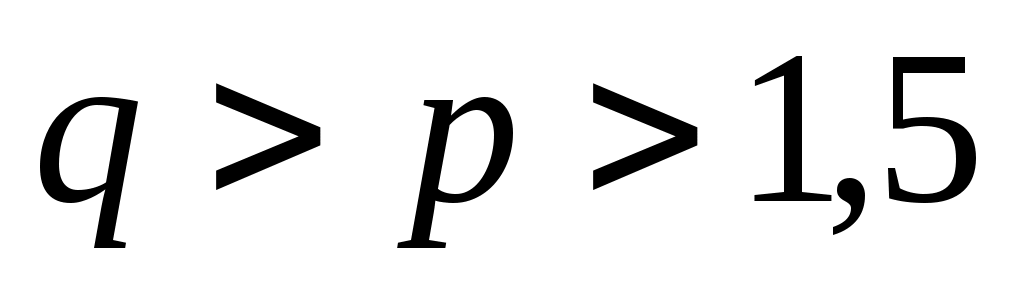 неравенство (2) справедливо. неравенство (2) справедливо.
б) на интервале 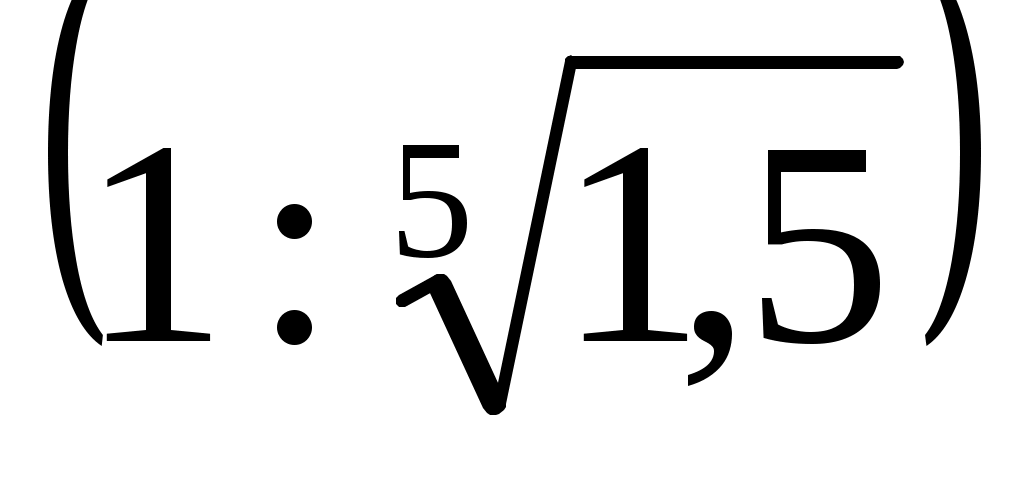 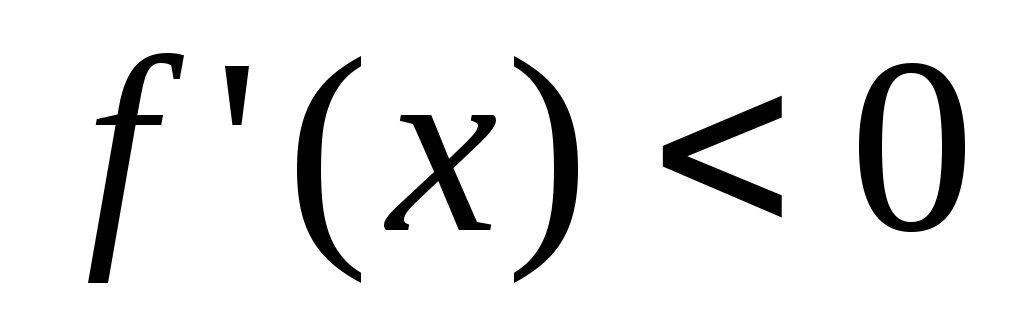 , т.е. , т.е. 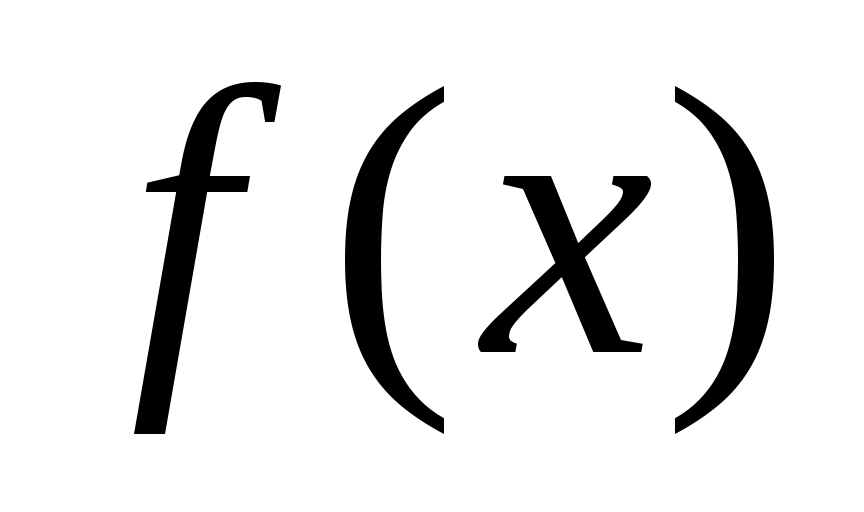 убывает. Поэтому при любых убывает. Поэтому при любых 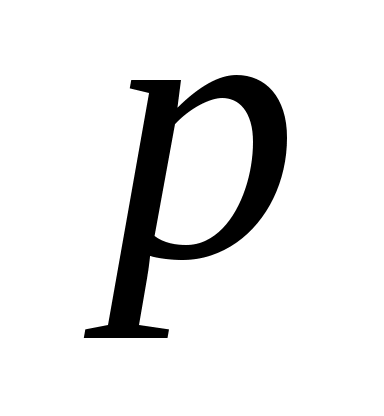 и и 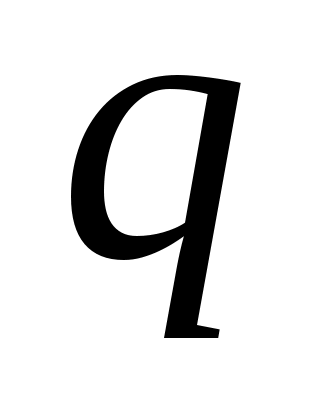 , для которых , для которых 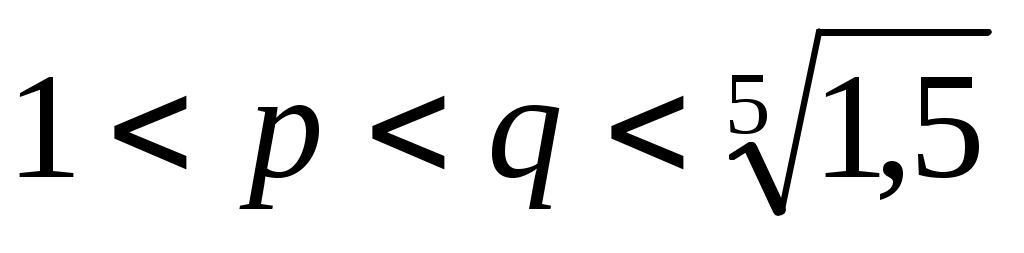 , неравенство (2) неверно, а верно неравенство противоположного смысла: , неравенство (2) неверно, а верно неравенство противоположного смысла: 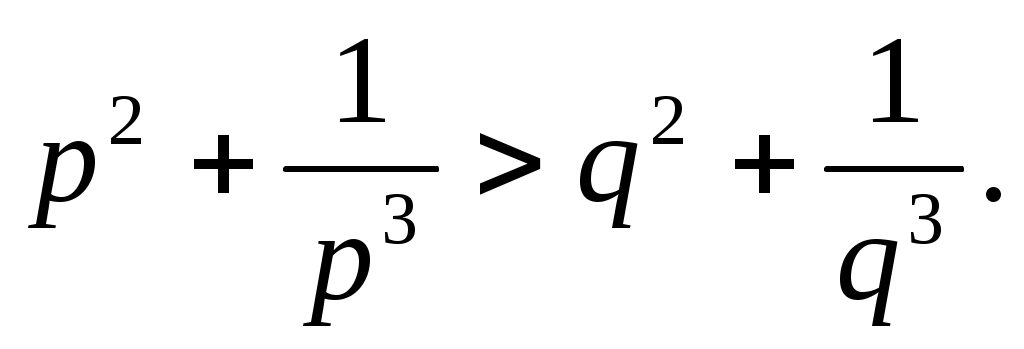
Задача_4'>Задача 3. Доказать неравенство: 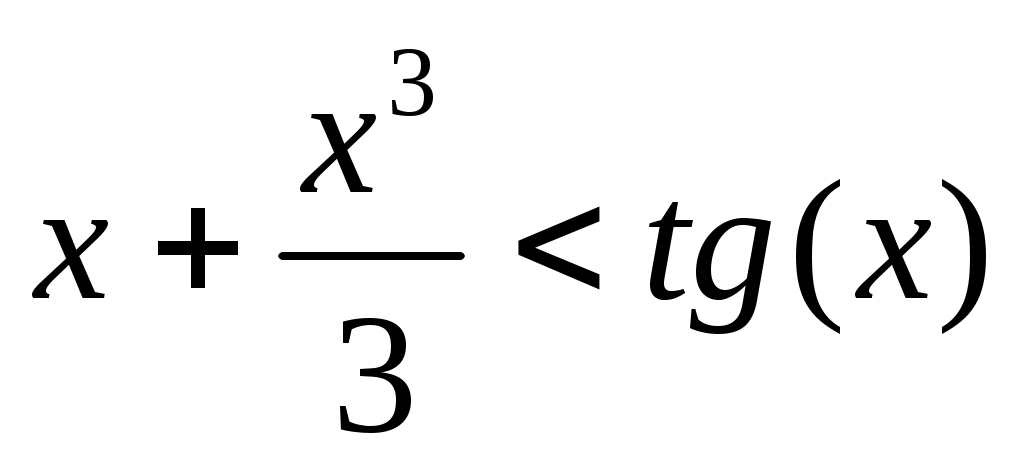 при при 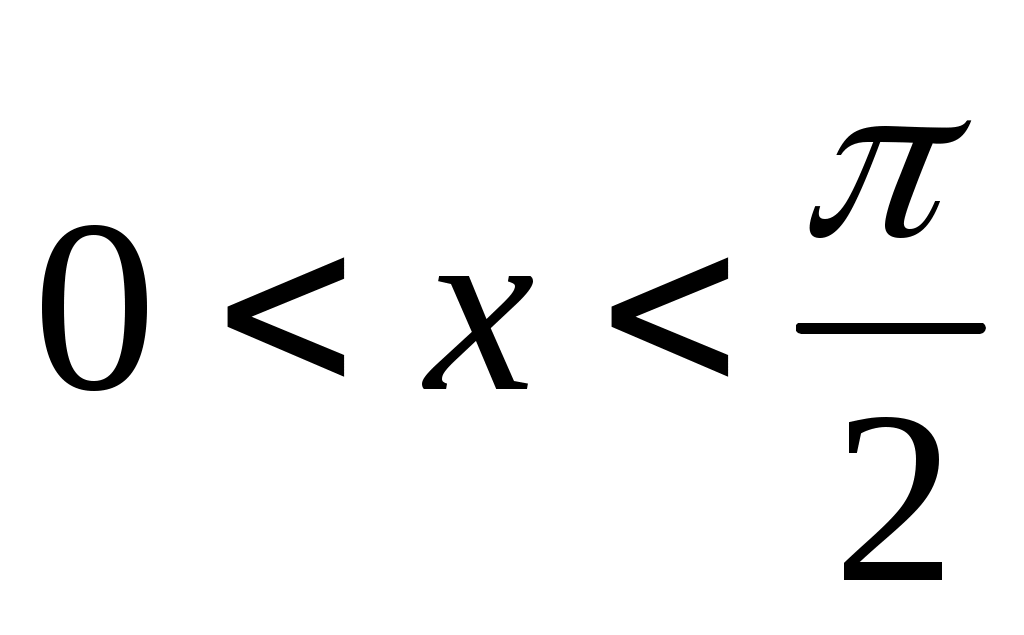 (3). (3).
Воспользуемся теоремой 2. 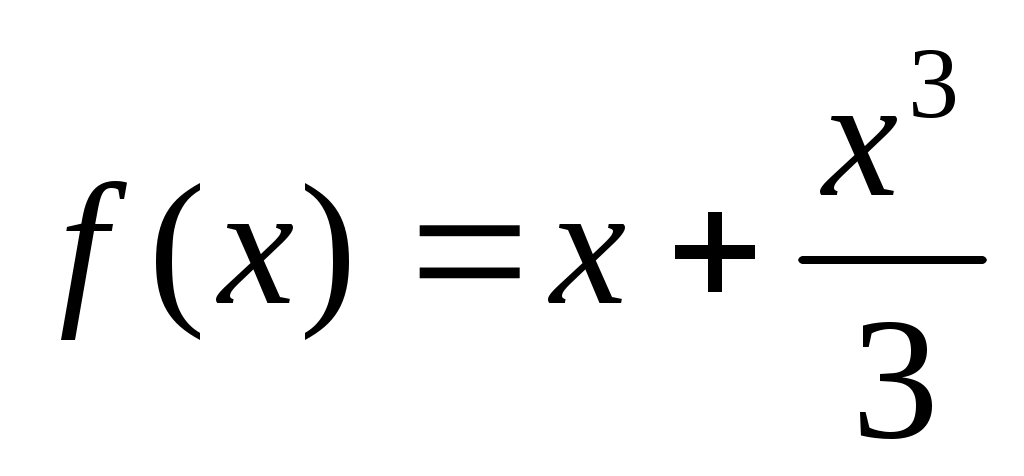 и и 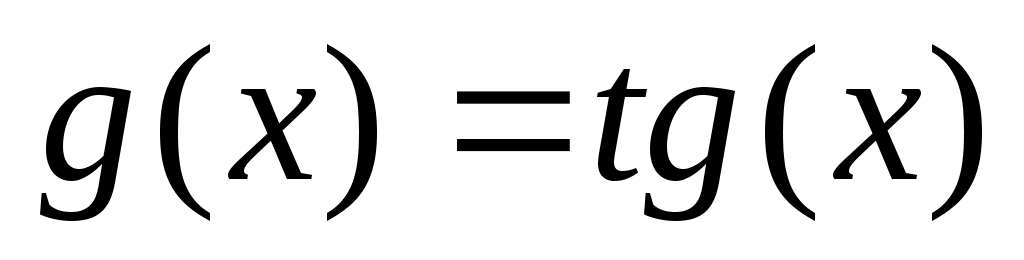 , верно неравенство , верно неравенство 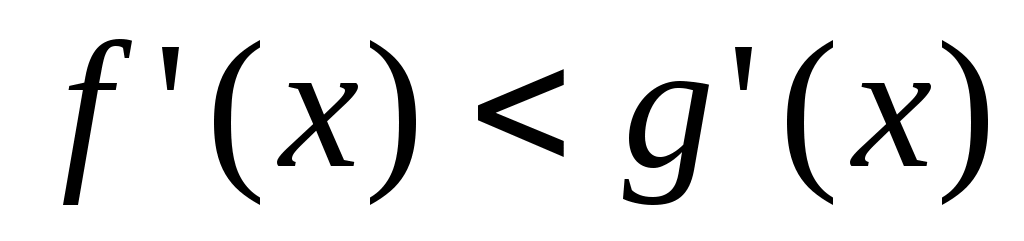 : : 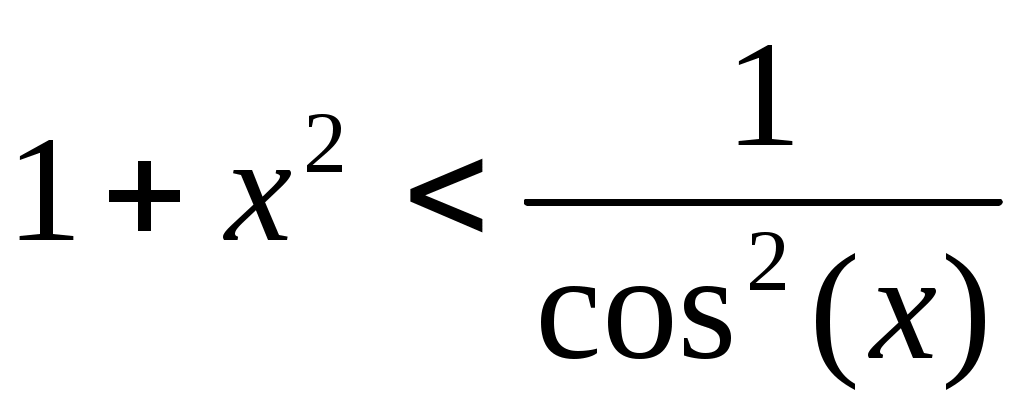 на промежутке на промежутке 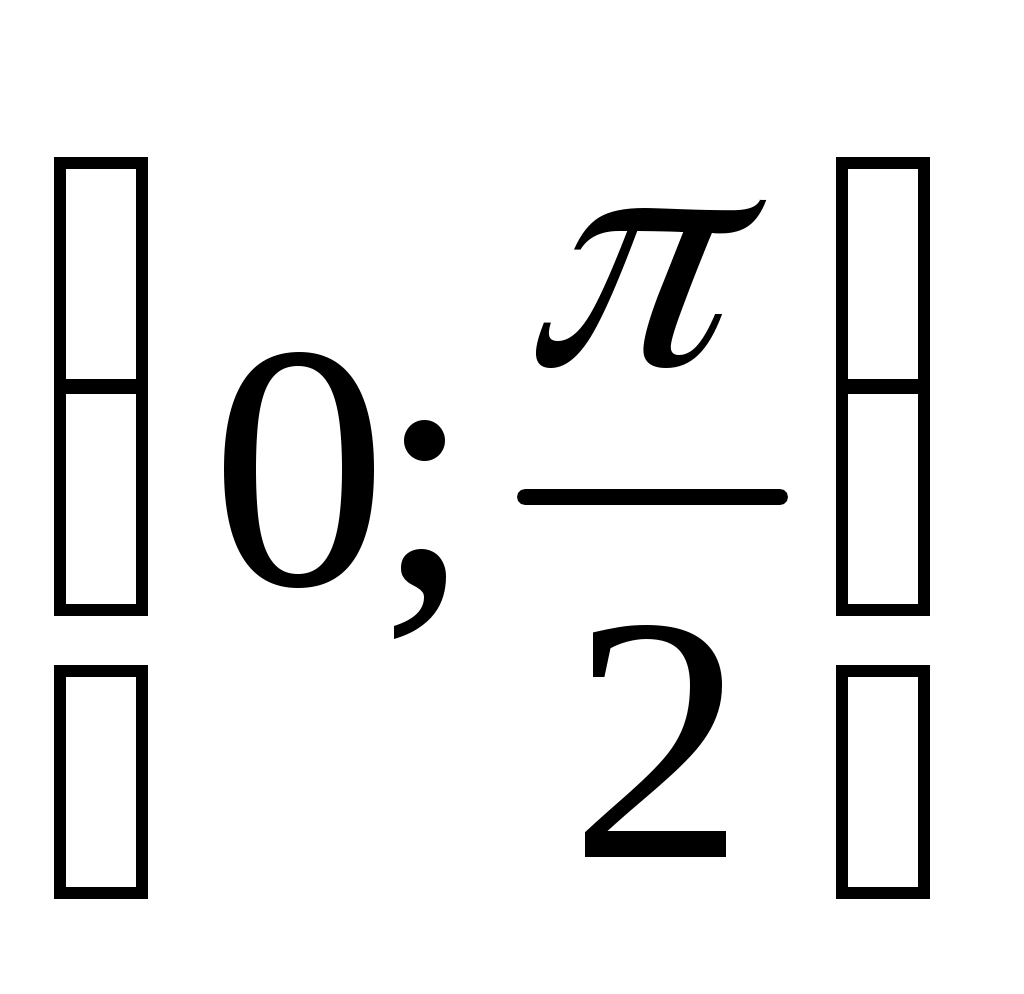 и выполнимо условие и выполнимо условие 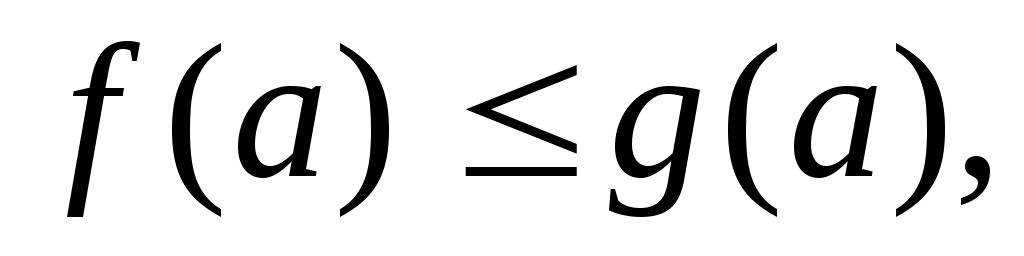 где где  , в данном случае равно 0. Следовательно неравенство (3) верно. , в данном случае равно 0. Следовательно неравенство (3) верно.
Задача 4. Доказать неравенство: 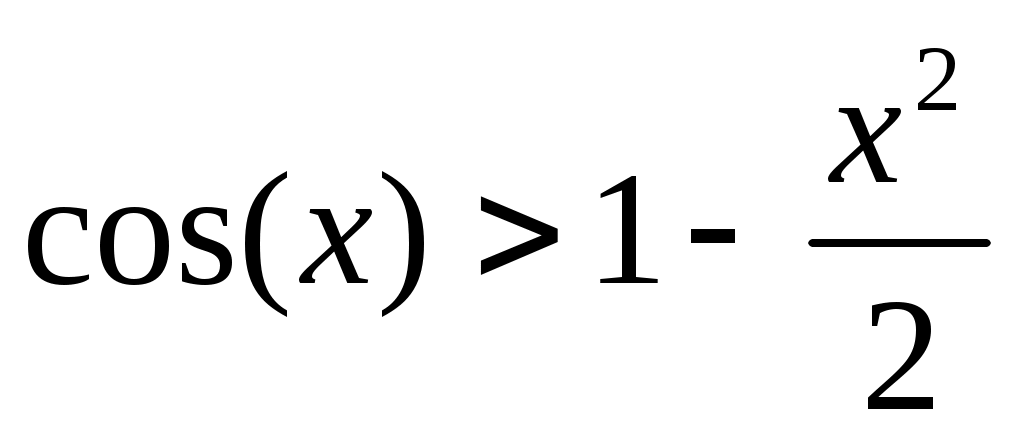 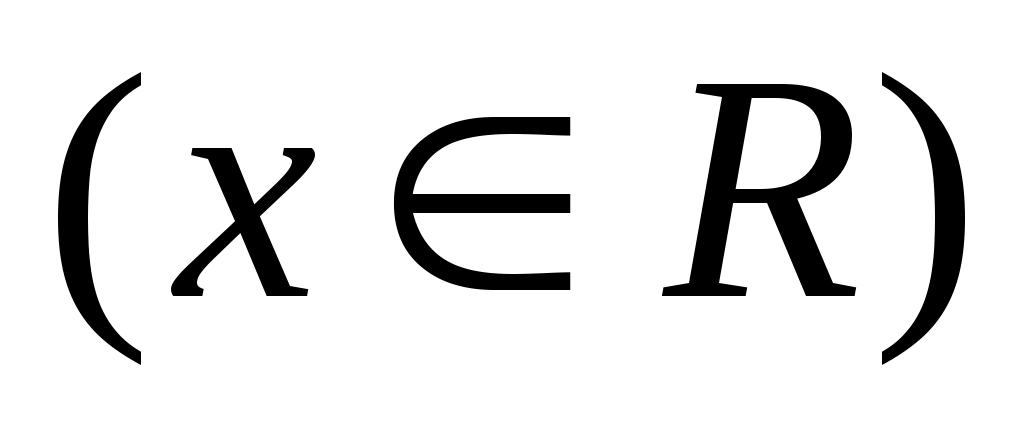 (4). (4).
Решение: 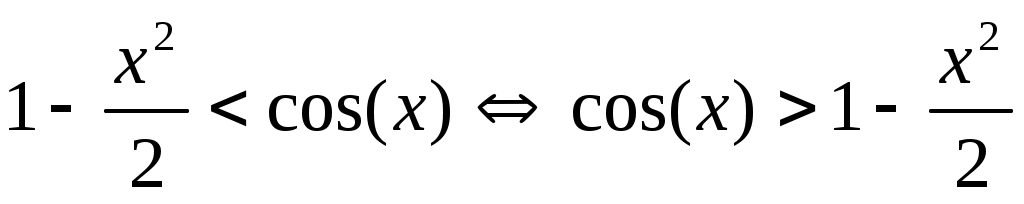 , , 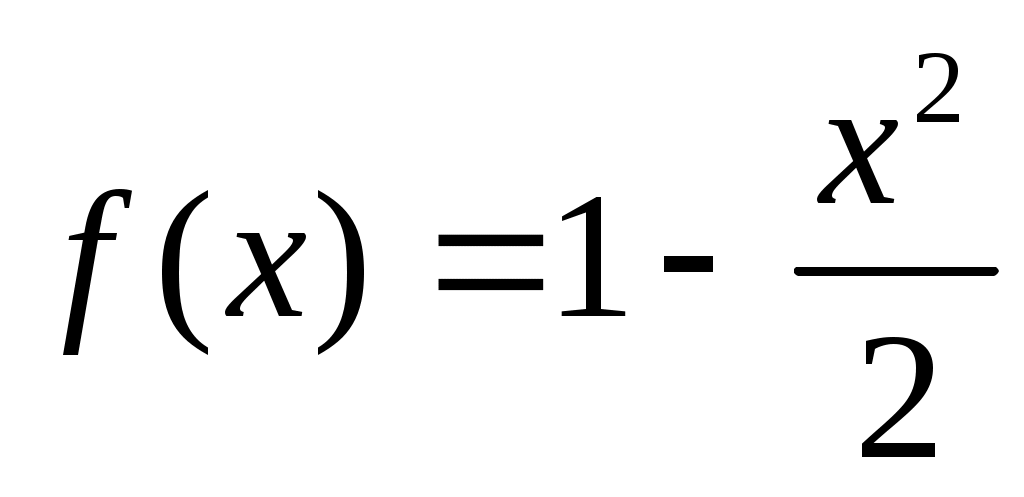 ; ; 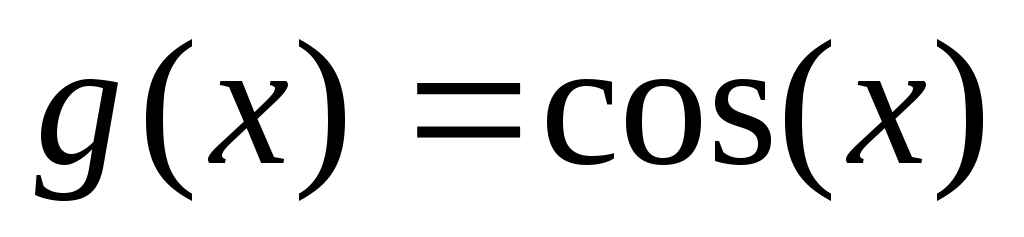
Неравенство  при любых при любых 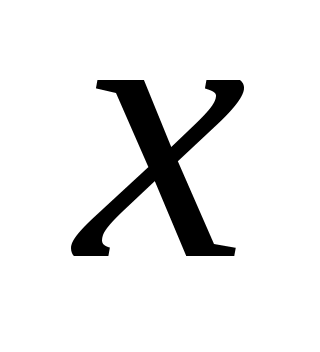 верно. Значит неравенство (4) верно. верно. Значит неравенство (4) верно.
Задача 5. Доказать, что если 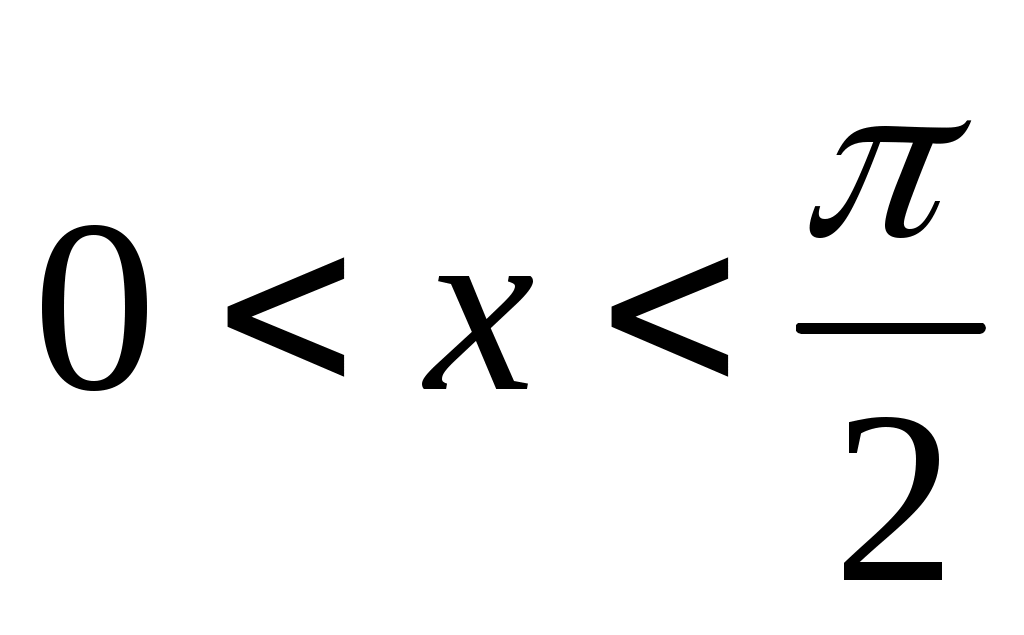 , то , то 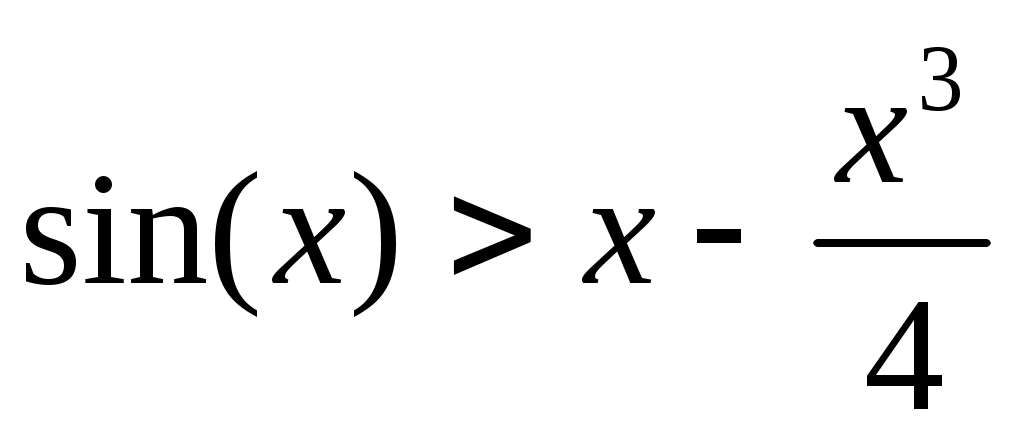 (5). (5).
Решение: Пусть 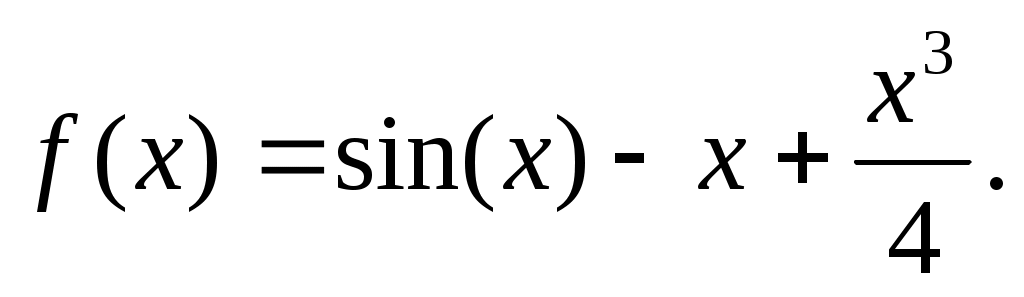 Тогда Тогда
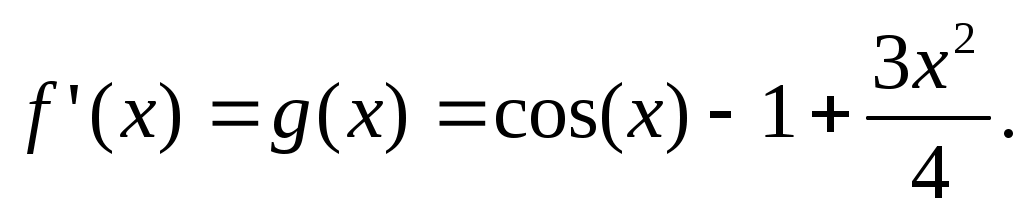
Чтобы найти, при каких значениях 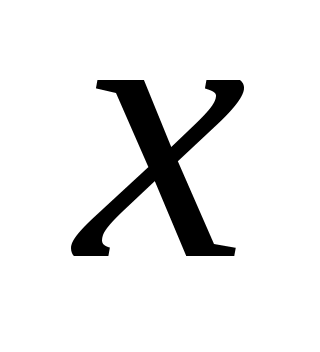 функция функция 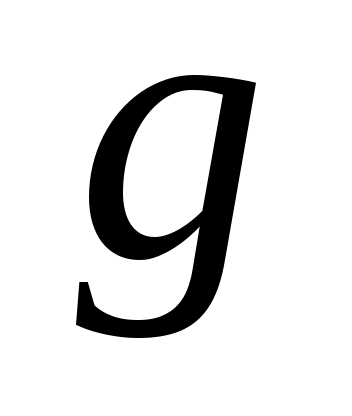 положительная, исследуем ее производную положительная, исследуем ее производную 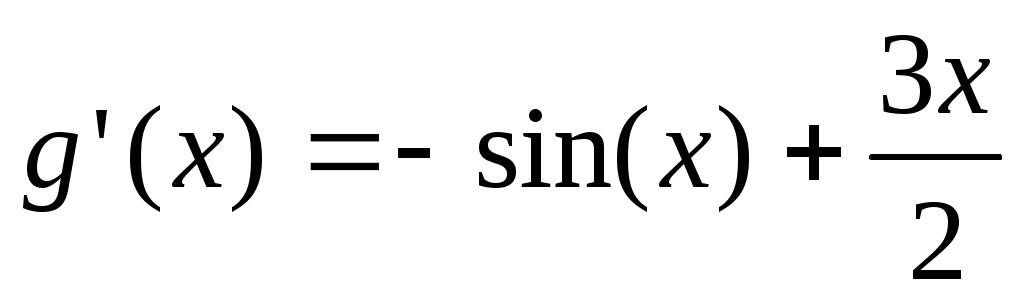 . Так как при . Так как при 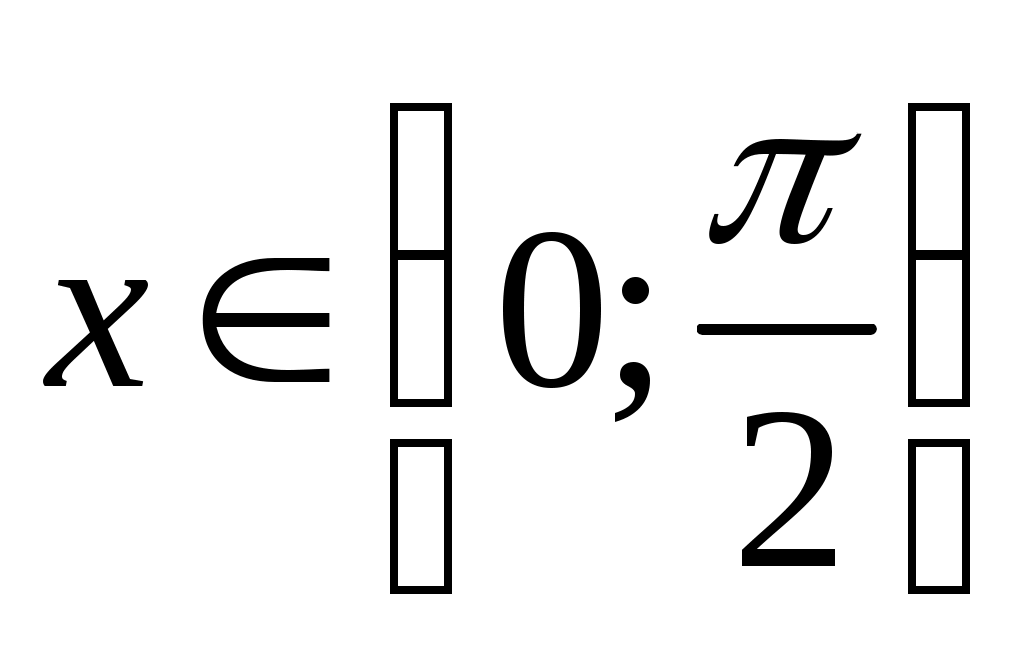 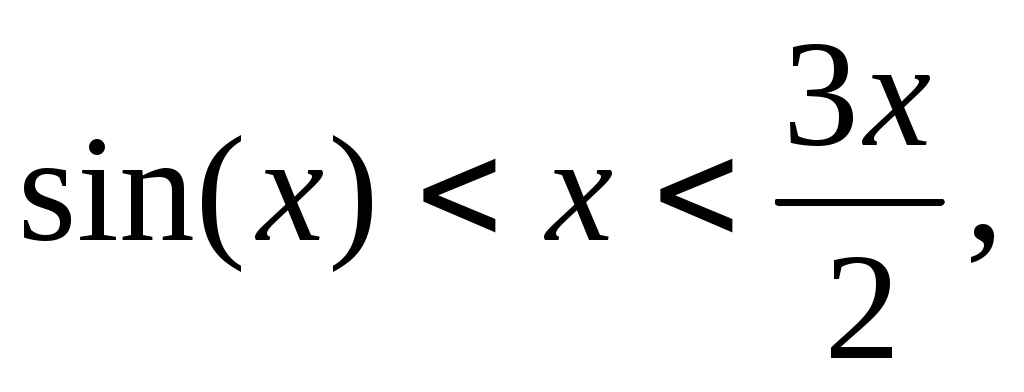 то то 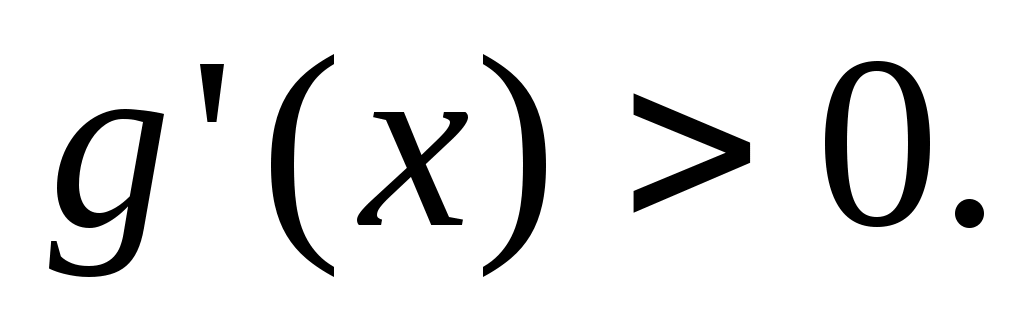
Следовательно, функция 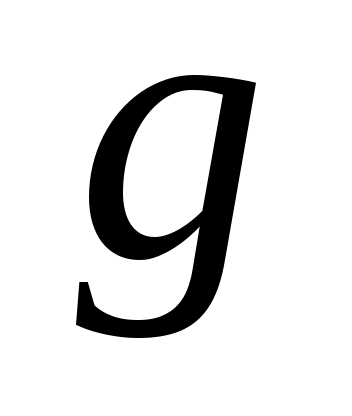 возрастает при возрастает при 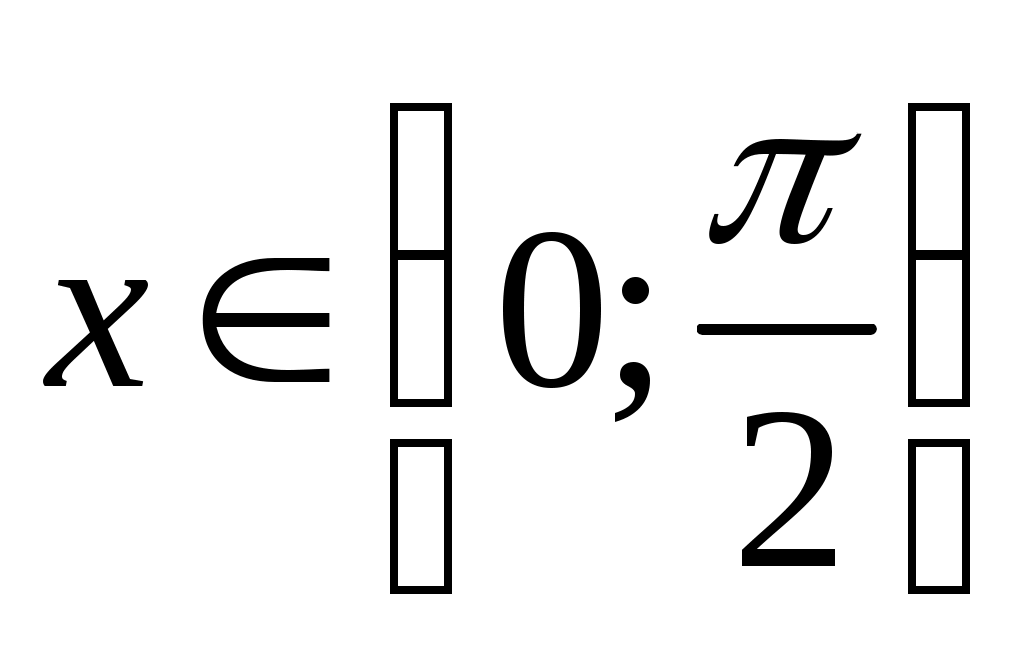 . Учитывая, что . Учитывая, что 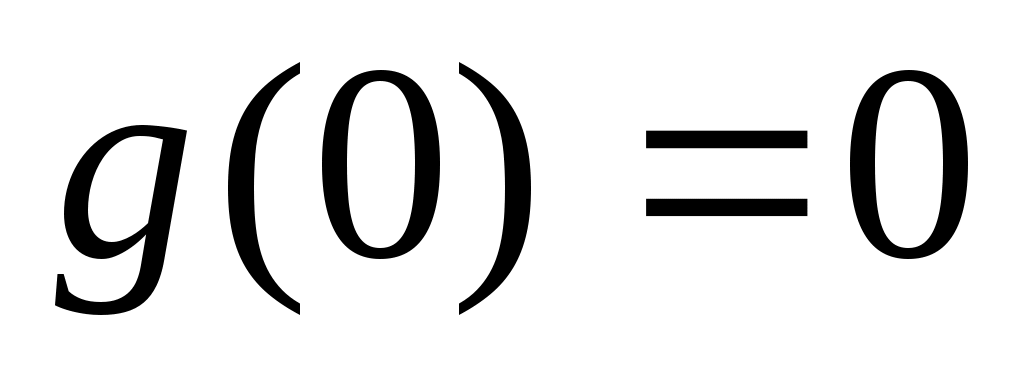 и и 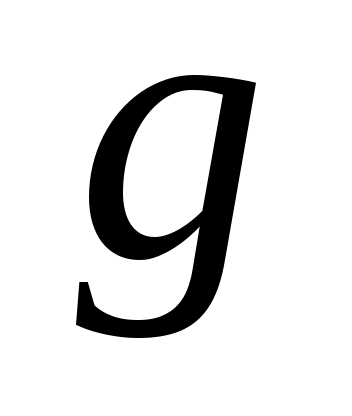 непрерывна, получаем непрерывна, получаем 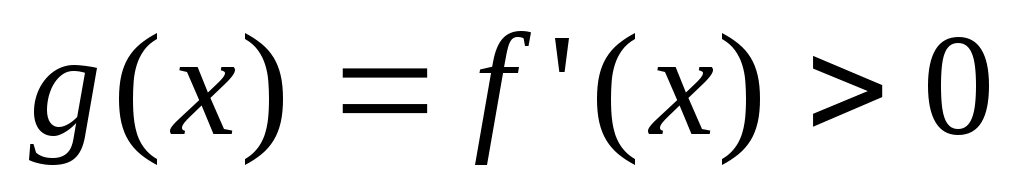 , при , при 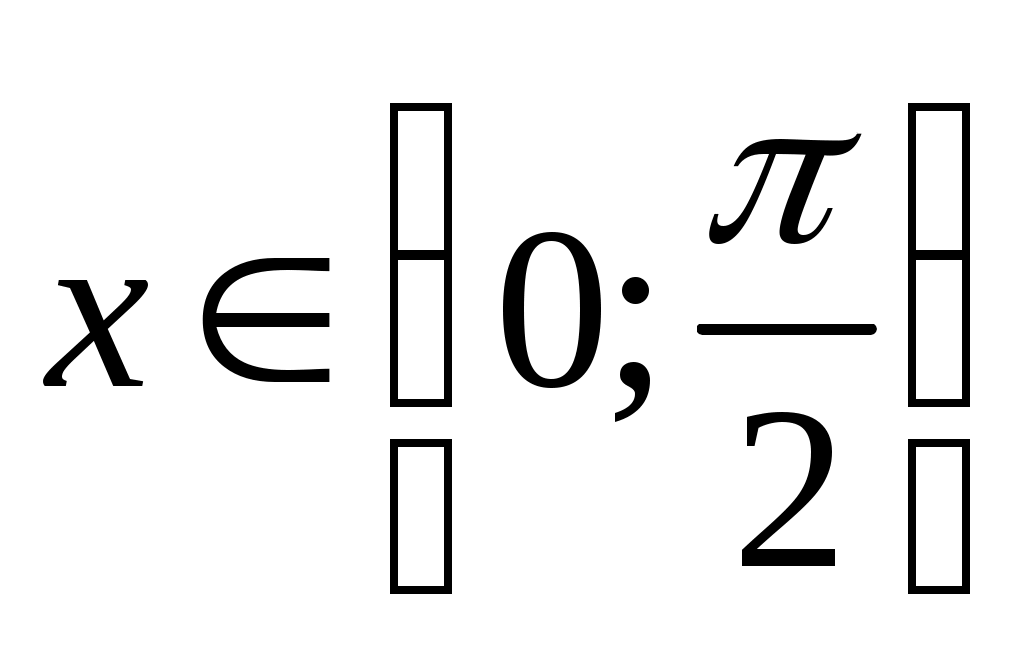 . .
Поэтому 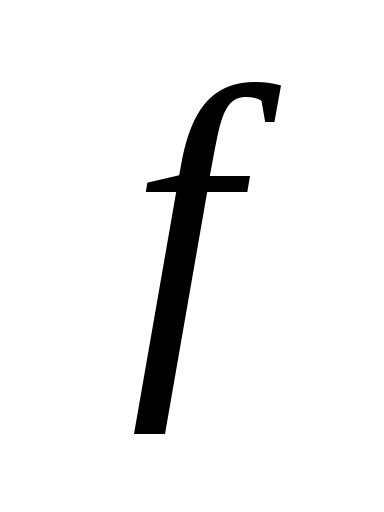 возрастает на рассматриваемом интервале. Поскольку возрастает на рассматриваемом интервале. Поскольку 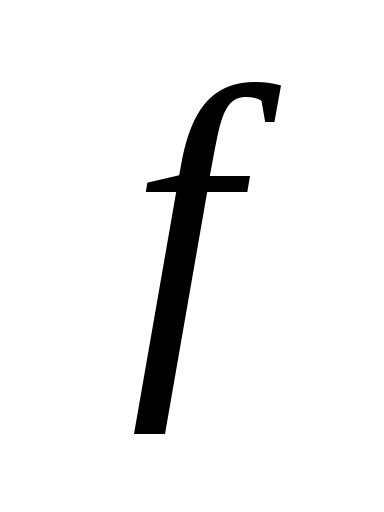 непрерывна и непрерывна и 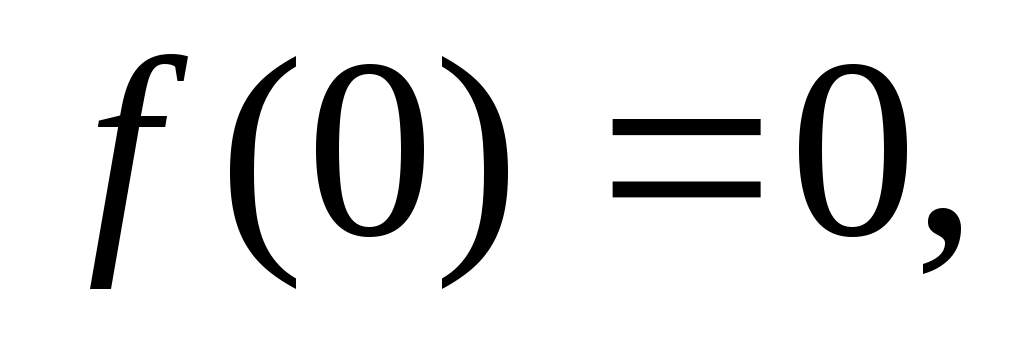 то то 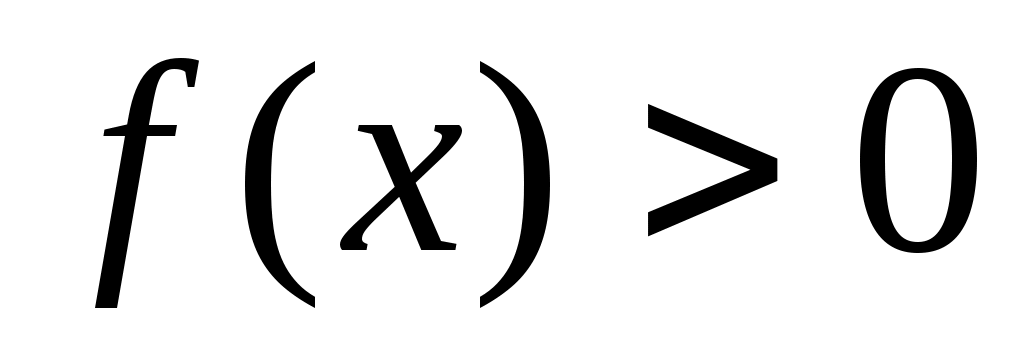 при при 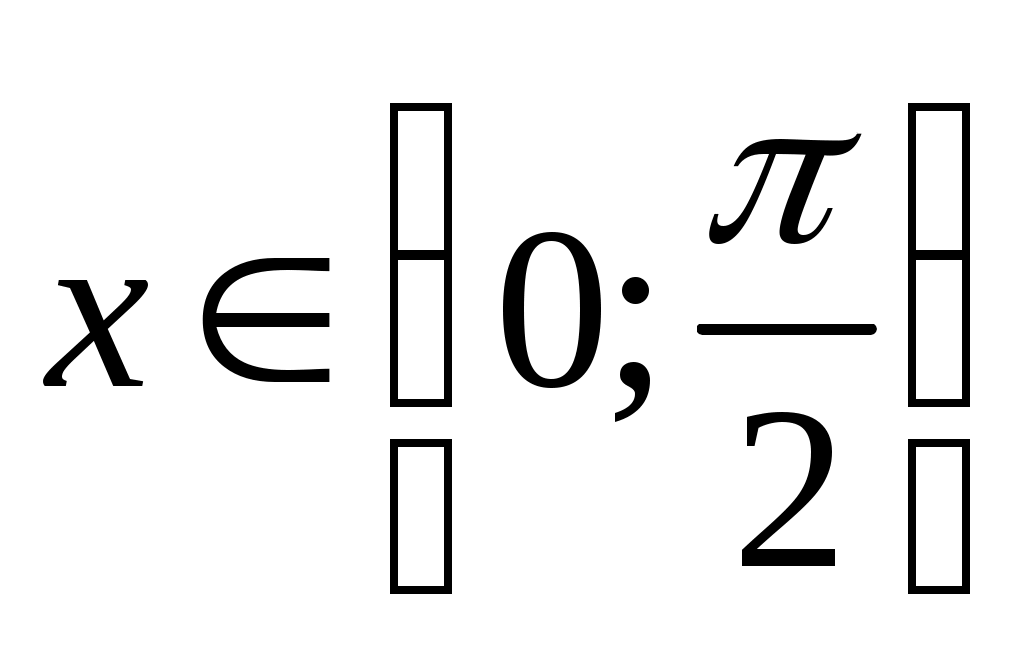 . Неравенство (5) верно. . Неравенство (5) верно.
Задача 6. Выясним, что больше при 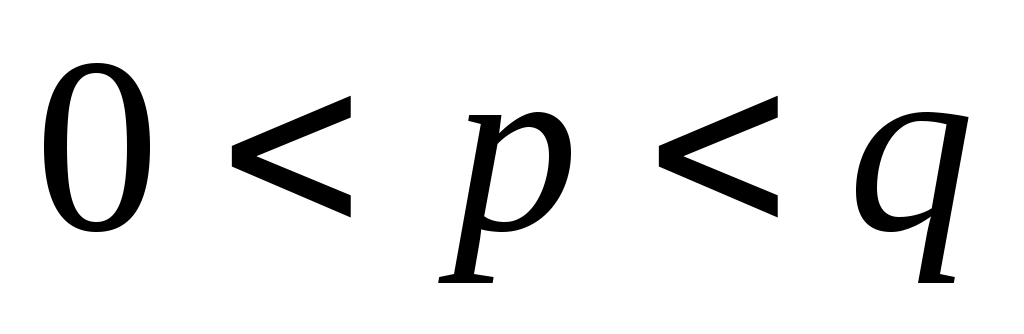 : : 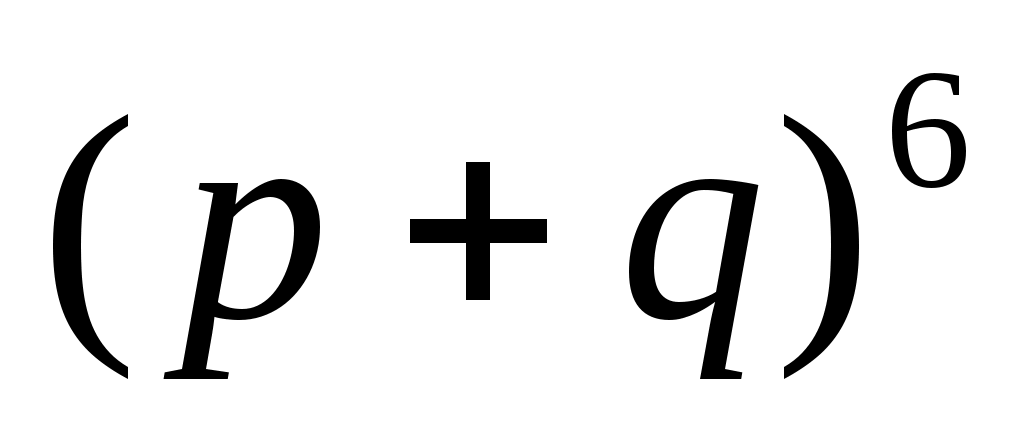 или или 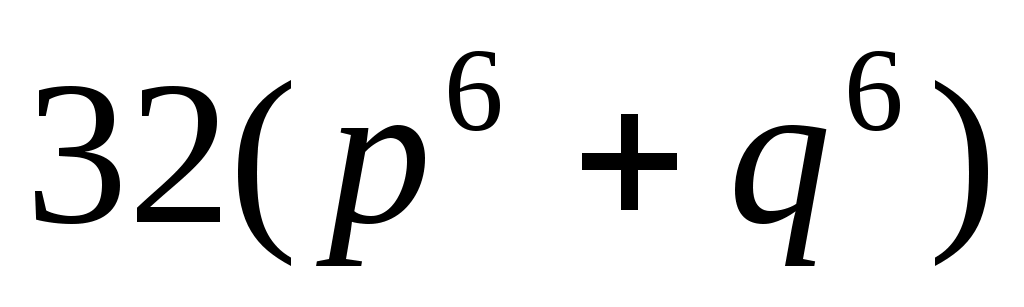 . .
Решение: Предстоит сравнить с числом 1 дробь 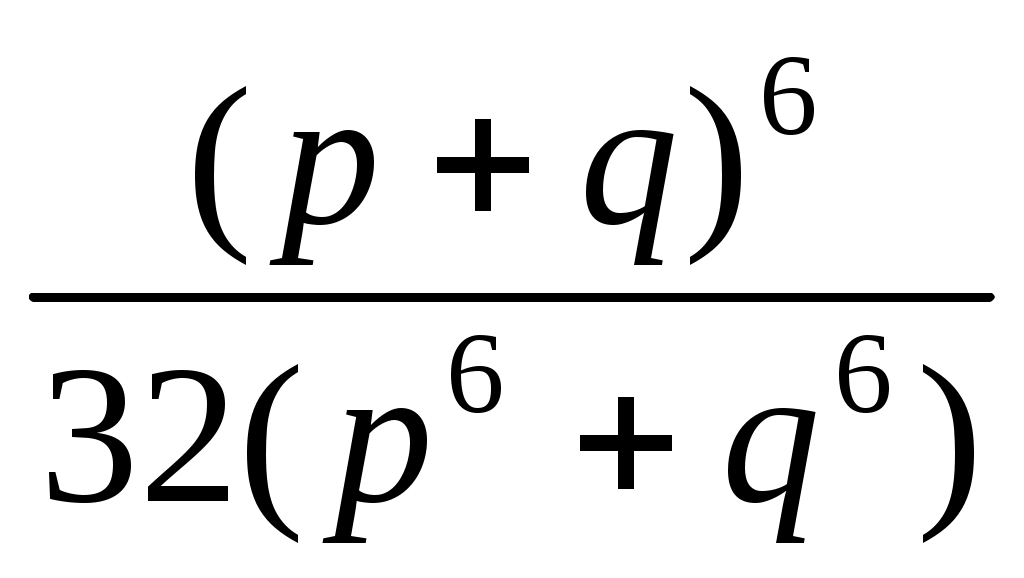 . .
Рассмотрим на 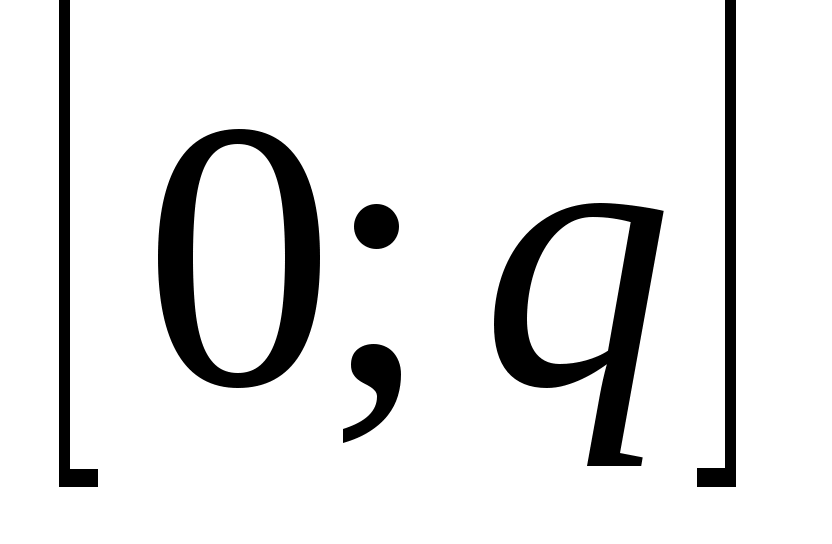 вспомогательную функцию вспомогательную функцию 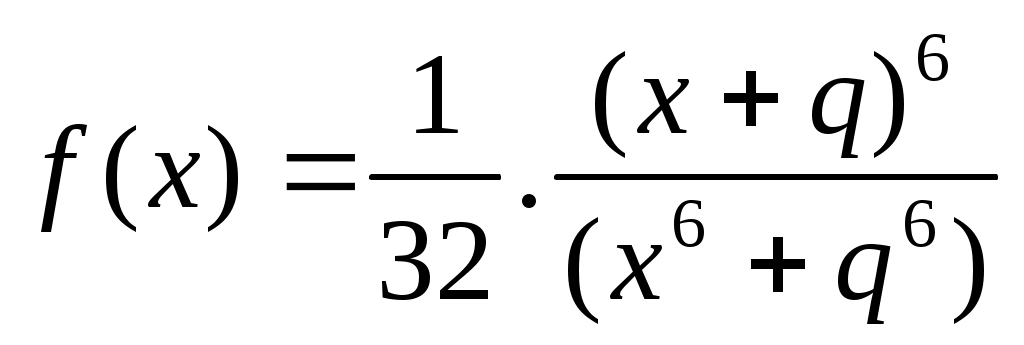 . .
Выясним, будет ли она монотонна на отрезке 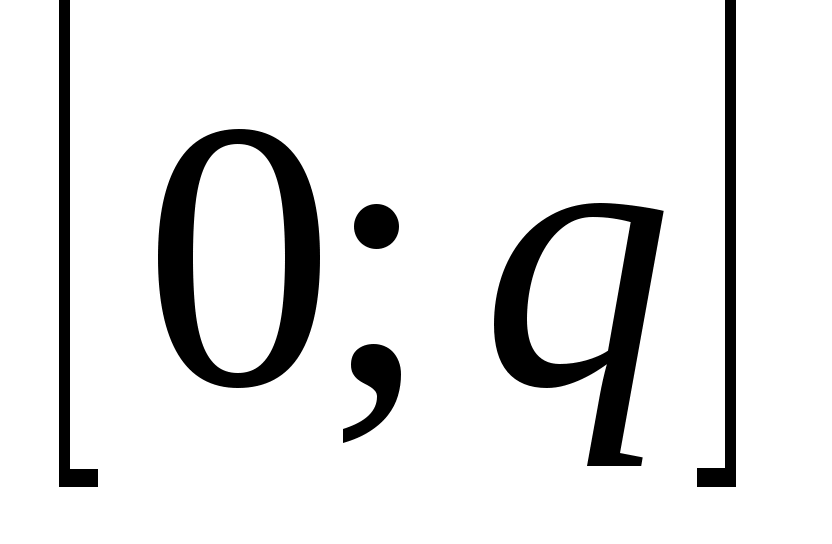 . Для этого найдем ее производную (по правилу дифференцирования дроби): . Для этого найдем ее производную (по правилу дифференцирования дроби):
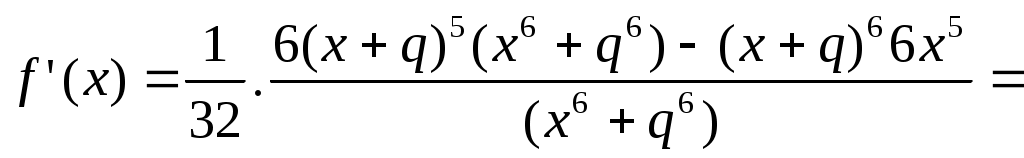
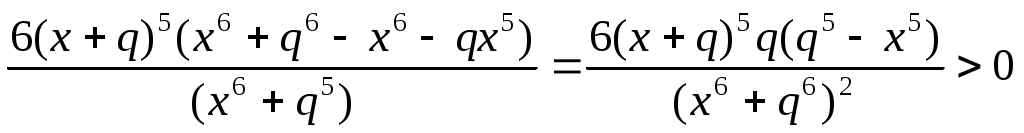 при при 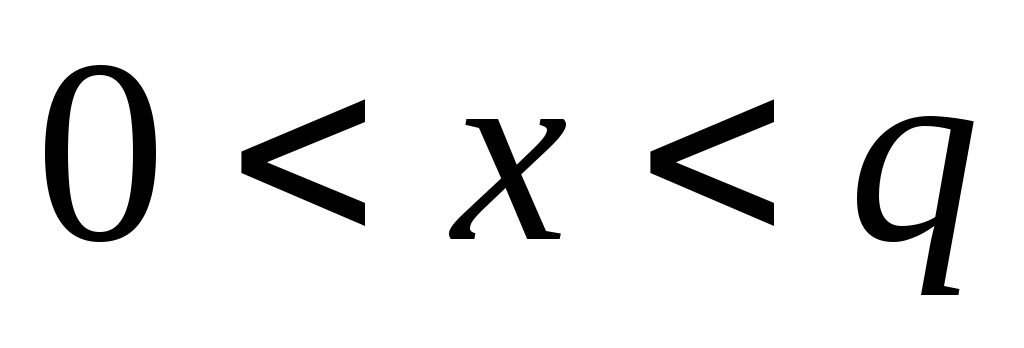 . .
В силу теоремы 1 функция 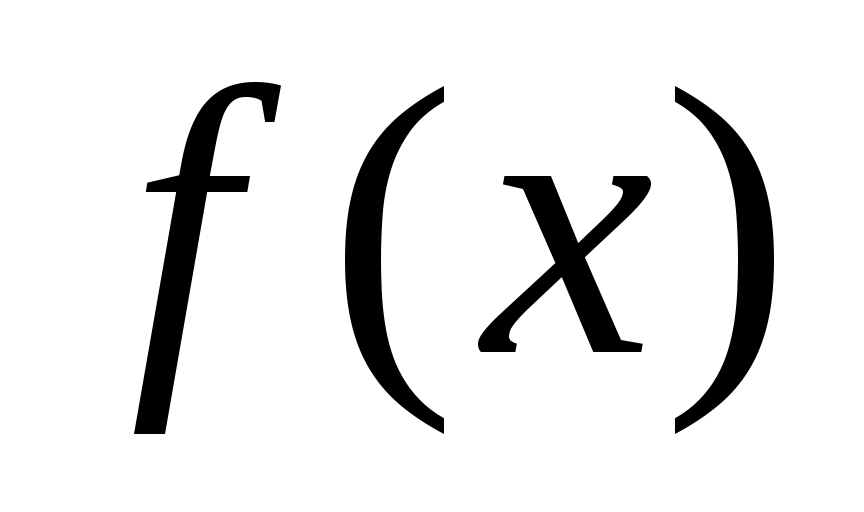 вырастает на отрезке вырастает на отрезке 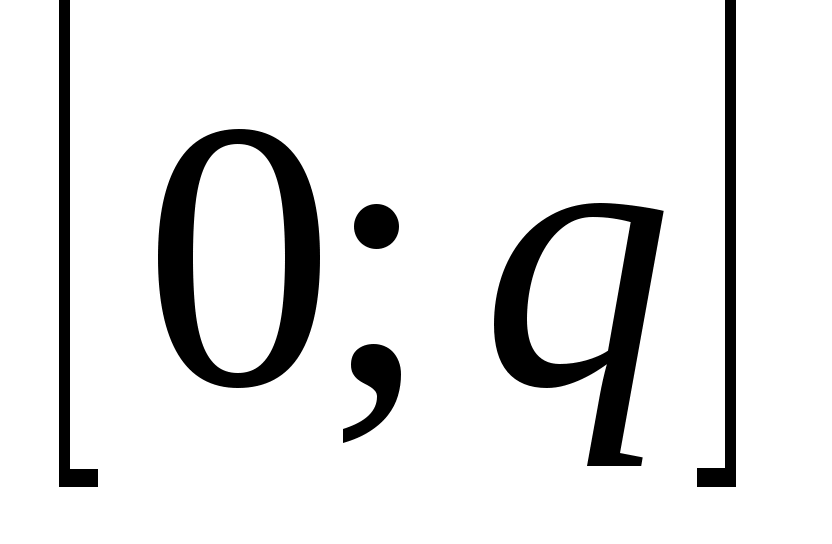 . Поэтому, при . Поэтому, при 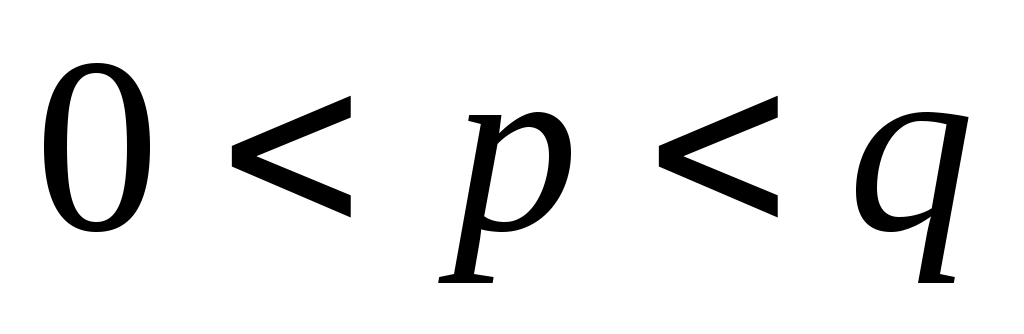 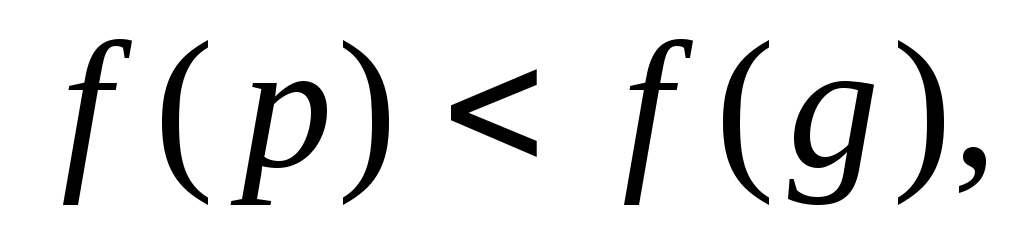 т.е. т.е. 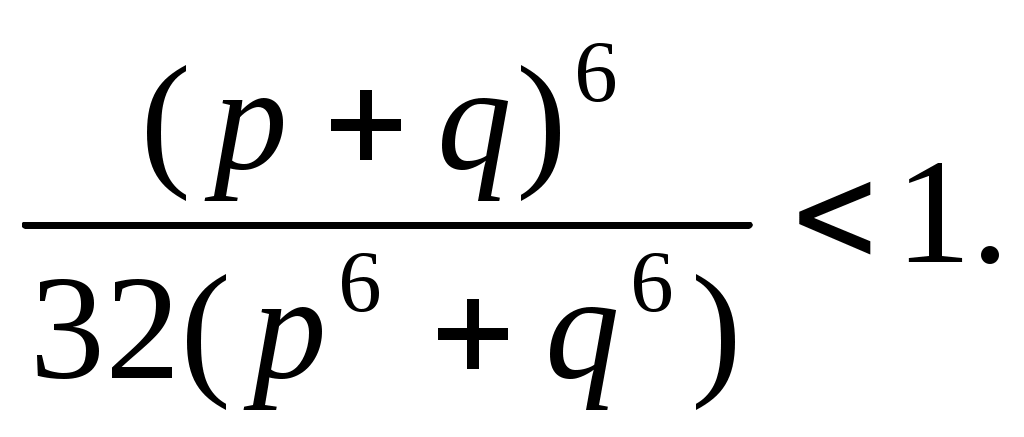
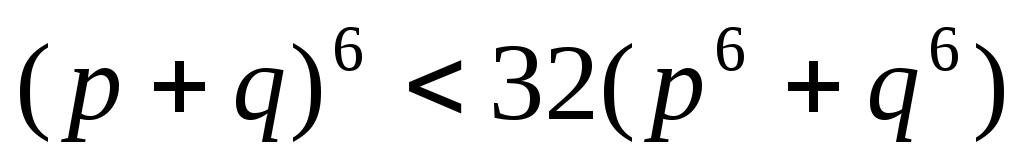 при при 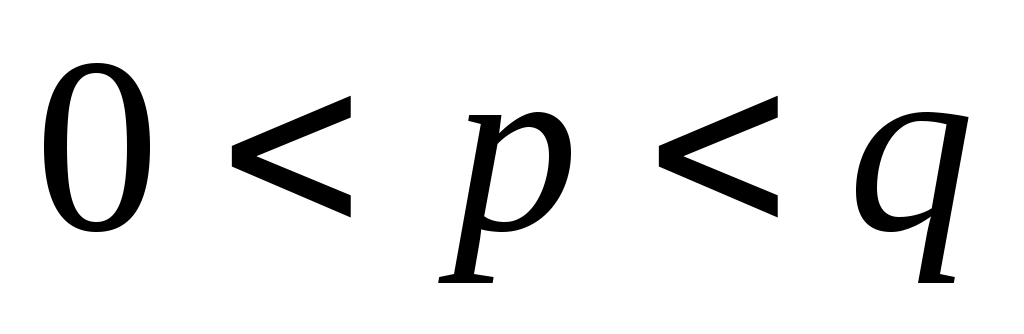 . .
При решении задачи (6) встретился полезный методический прием, если нежно доказать неравенство, в котором участвует несколько букв, то часто целесообразно одну из букв (в данном примере это была буква 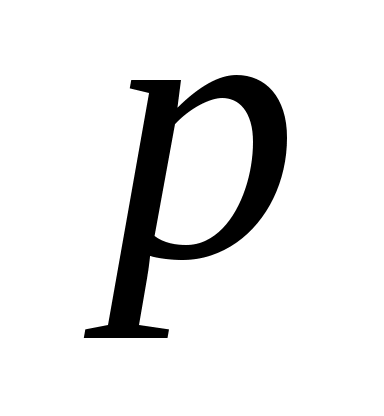 ) считать применимой (чтобы подчеркнуть это обстоятельство, мы ее заменяли буквой ) считать применимой (чтобы подчеркнуть это обстоятельство, мы ее заменяли буквой 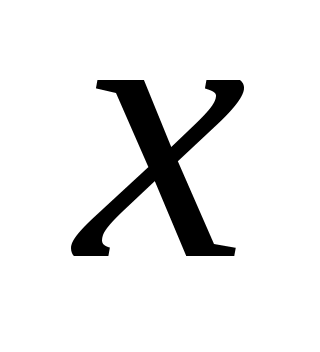 , а значение остальных букв (в данном случае значение буквы , а значение остальных букв (в данном случае значение буквы 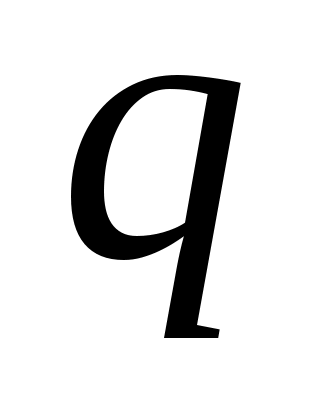 ) считать фиксированными. Иногда приходится при решении одной задачи применить указанный прием несколько раз. ) считать фиксированными. Иногда приходится при решении одной задачи применить указанный прием несколько раз.
Задача 7. Проверить, справедливо ли при любых положительных 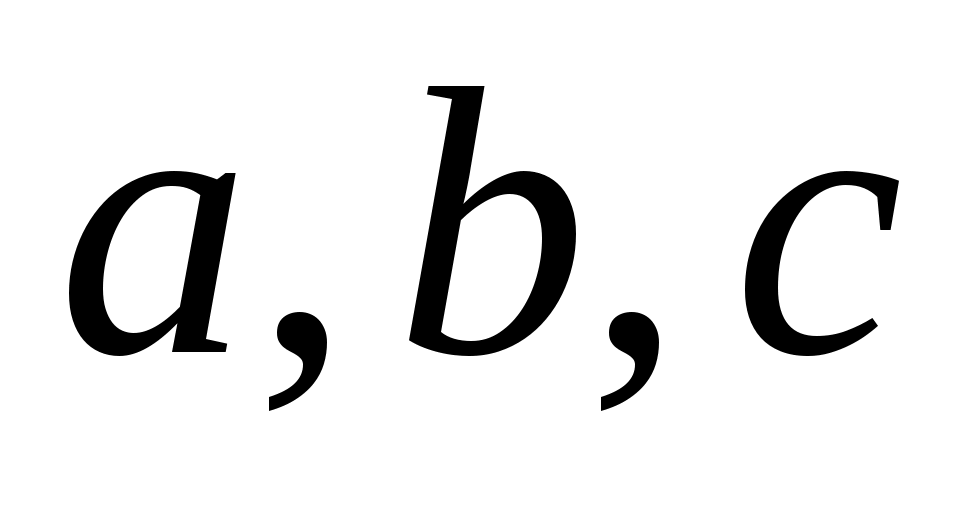 неравенство: неравенство: 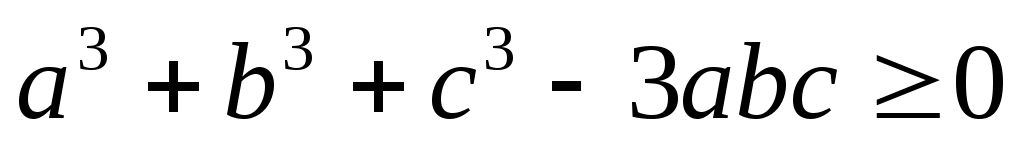 (6). (6).
Решение: Пусть 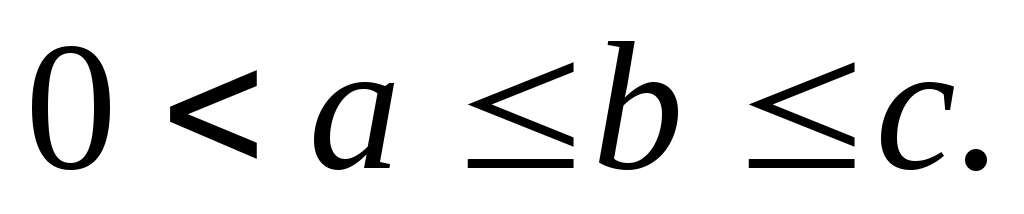 Рассмотрим функцию Рассмотрим функцию
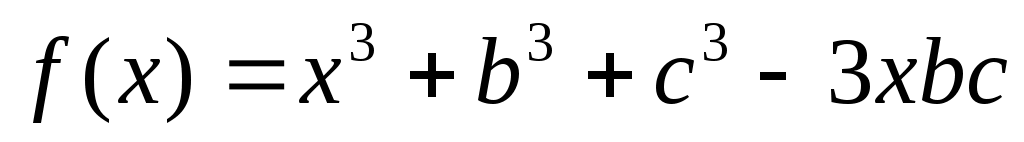 . .
При 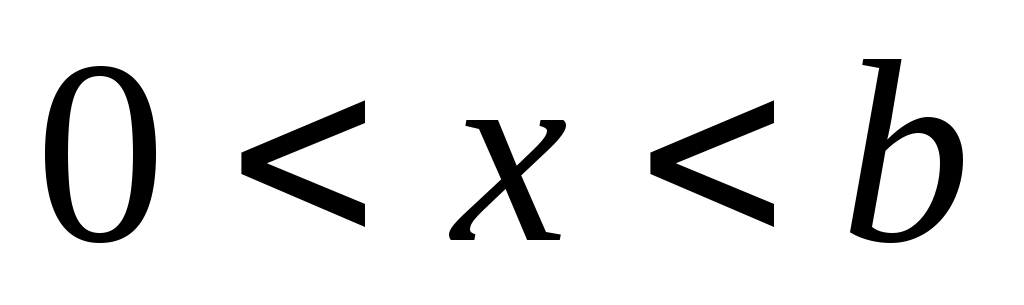 имеем имеем 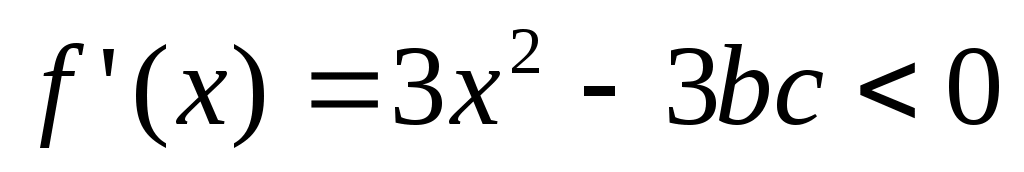 . .
Отсюда видно (теорема 1), что 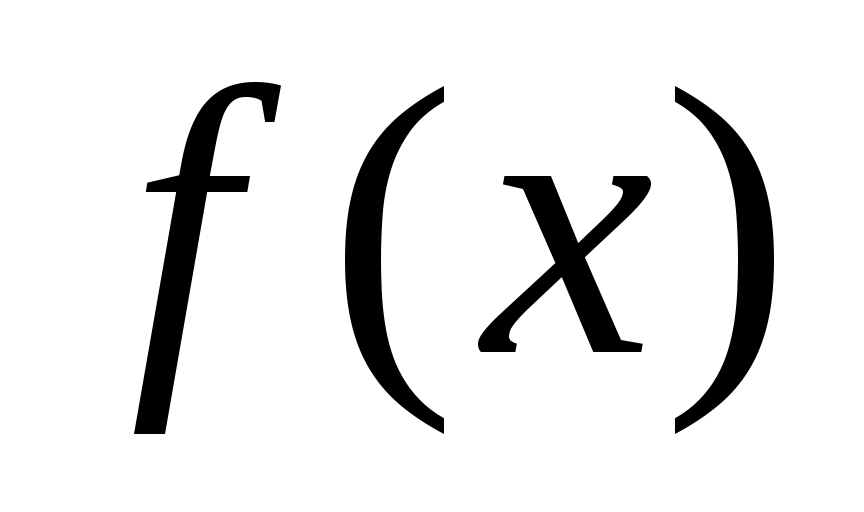 убывает на убывает на 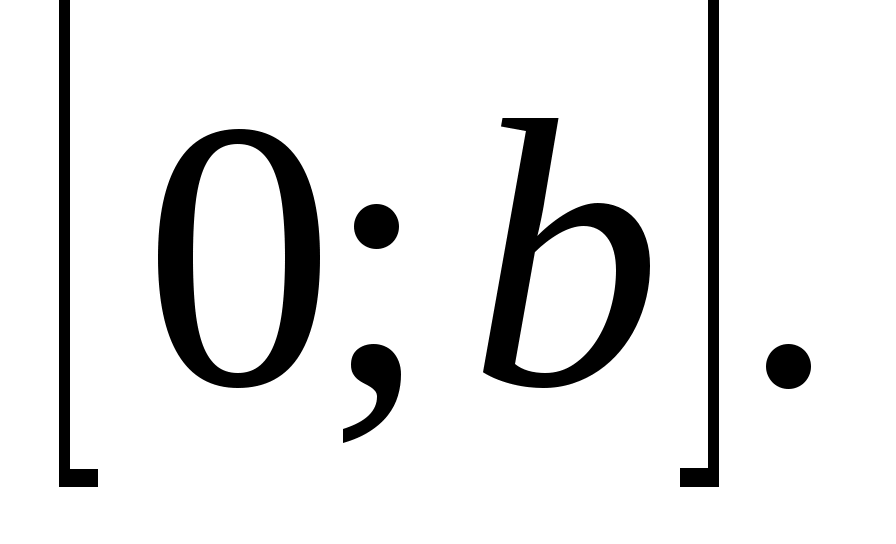 Поэтому при Поэтому при 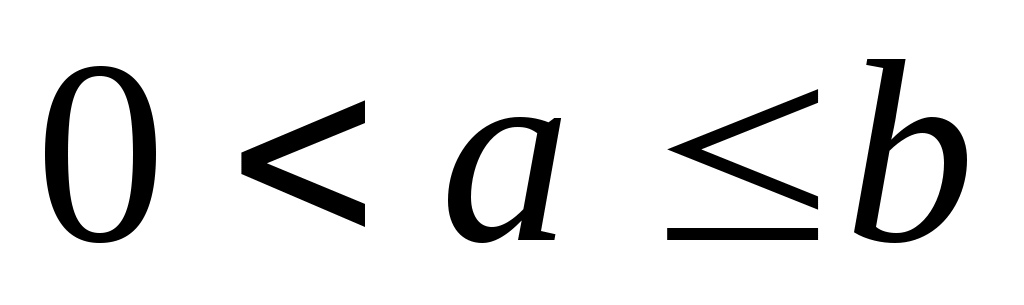 имеем имеем 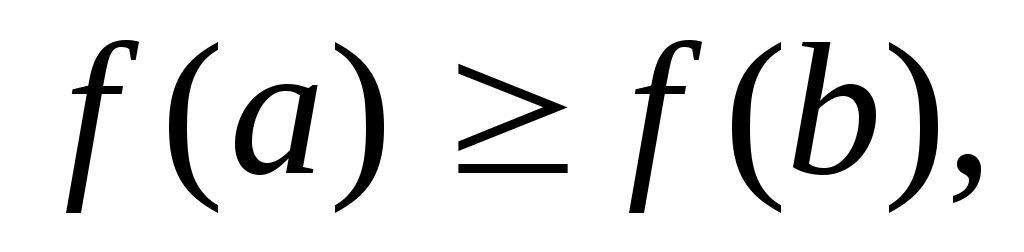 т.е. мы получили неравенство: т.е. мы получили неравенство:
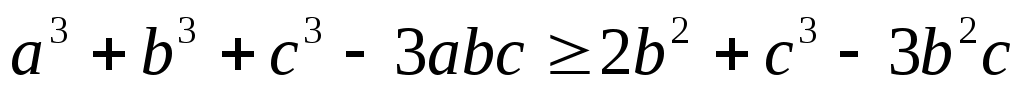 (7). (7).
Теперь рассмотрим другую вспомогательную функцию 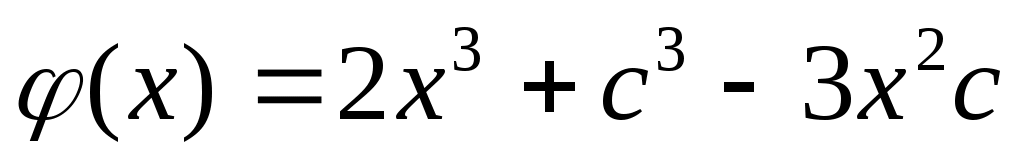 . При . При 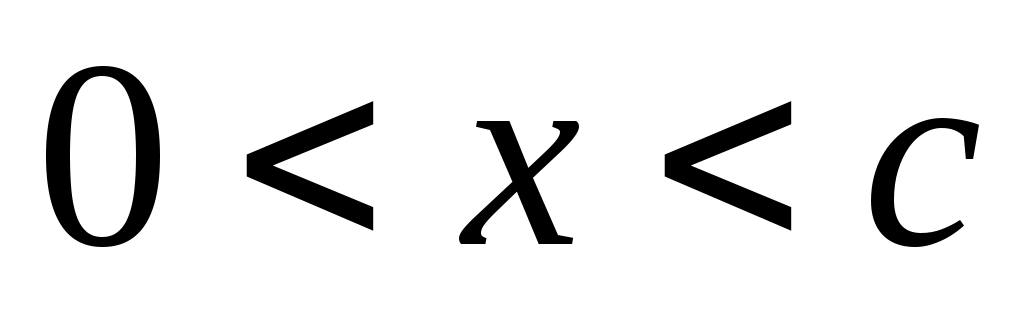 имеем: имеем: 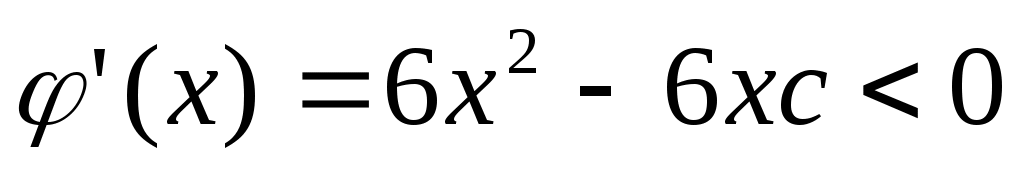
Следовательно, 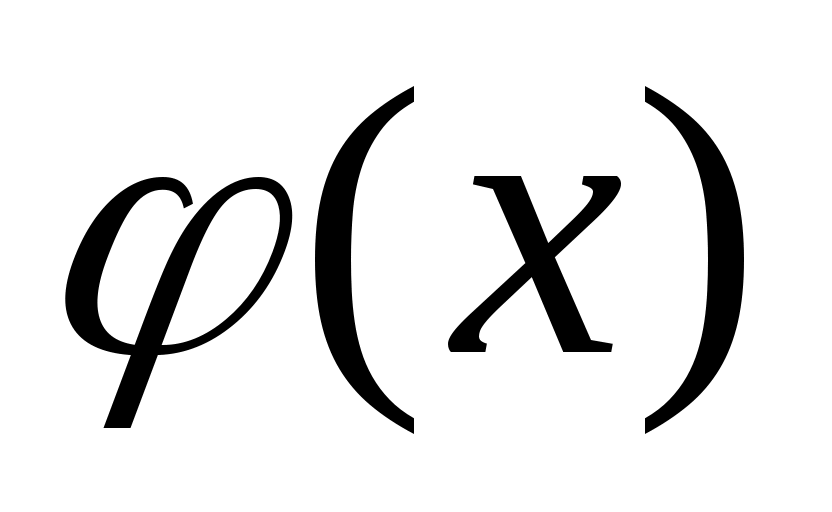 убывает на убывает на 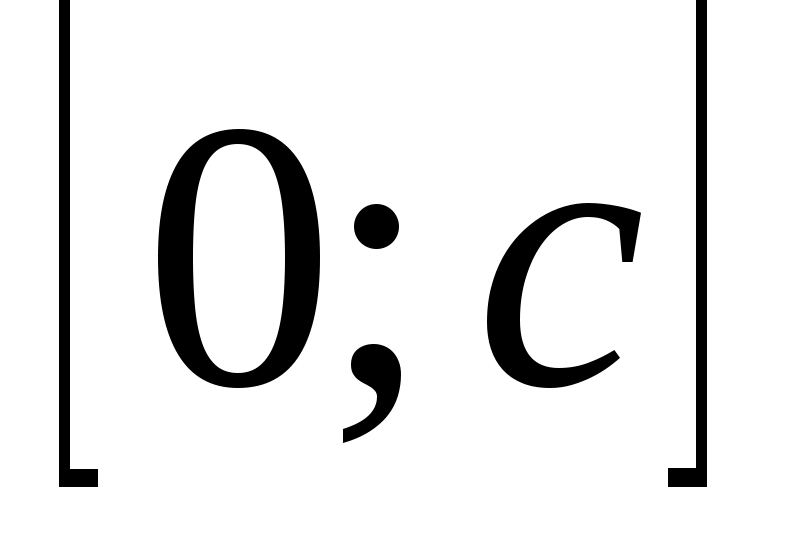 , т.е. , т.е. 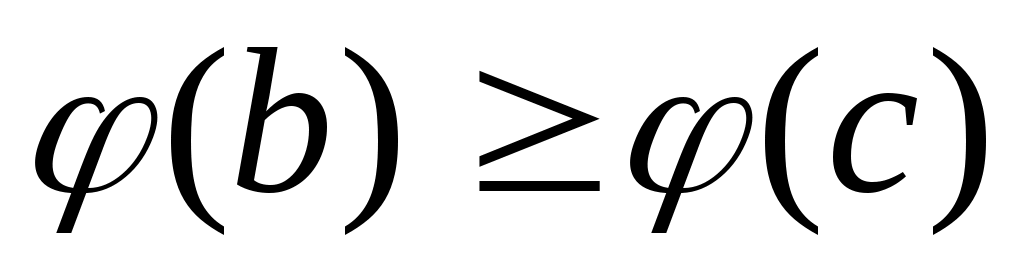 при при 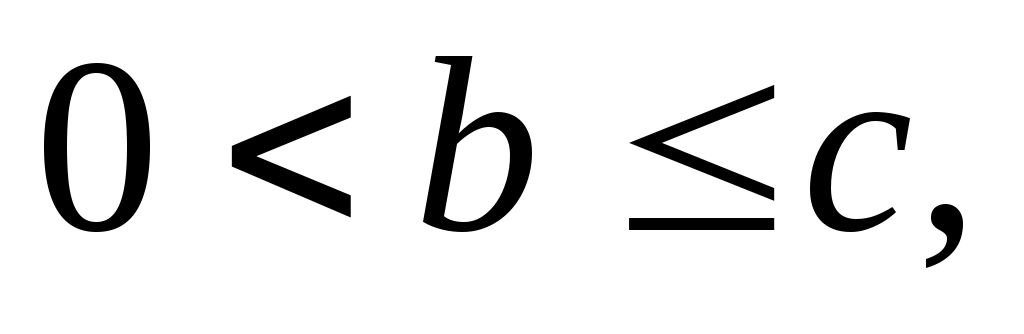 значит, значит, 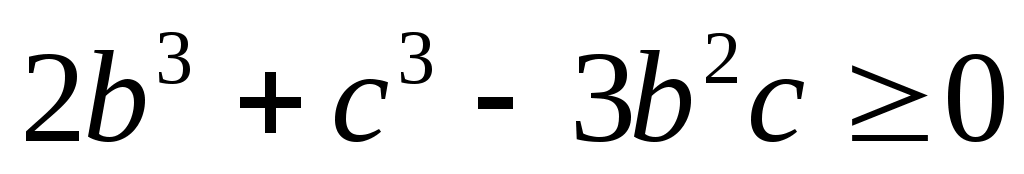 (8), (8),
Из неравенств (7) и (8) следует неравенство (6). Для выяснения истинности неравенств иногда удобно воспользоваться следующим утверждением, которое непосредственно вытекает из теоремы 1:
Теорема 3: Пусть функция 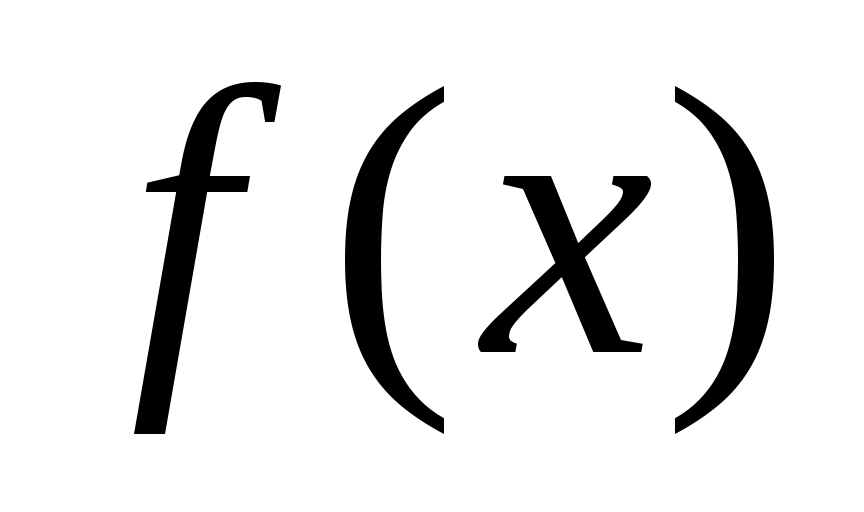 непрерывна на непрерывна на 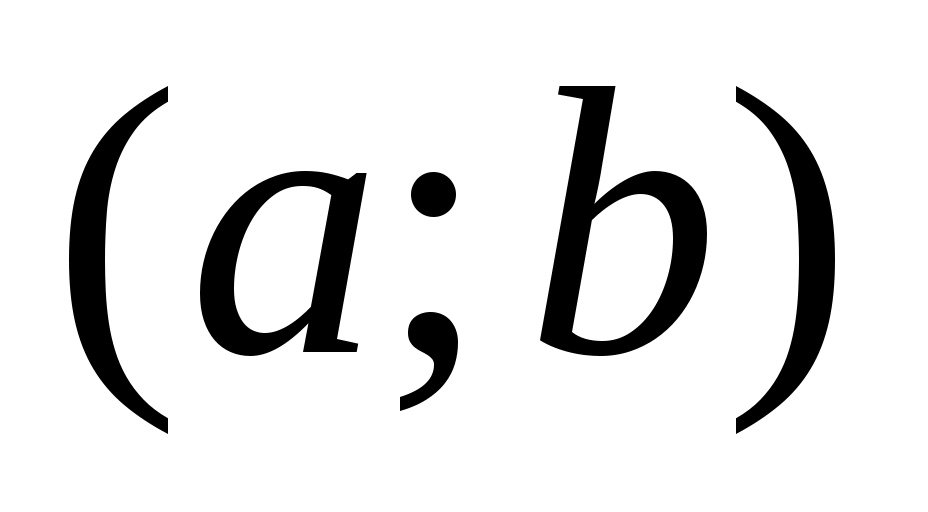 и пусть имеется такая точка с из и пусть имеется такая точка с из 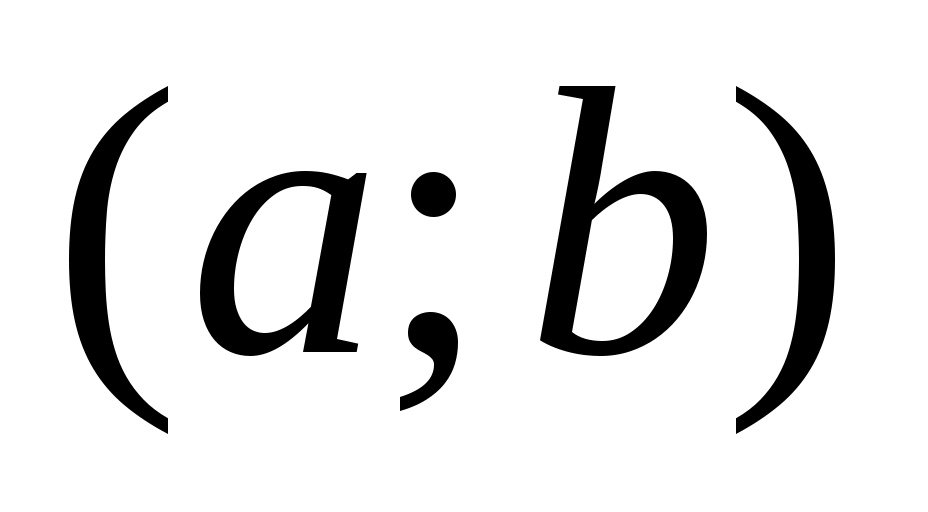 , что , что 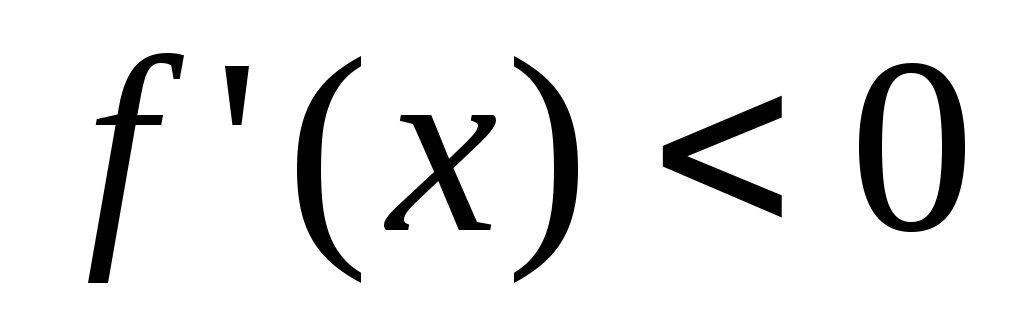 на на 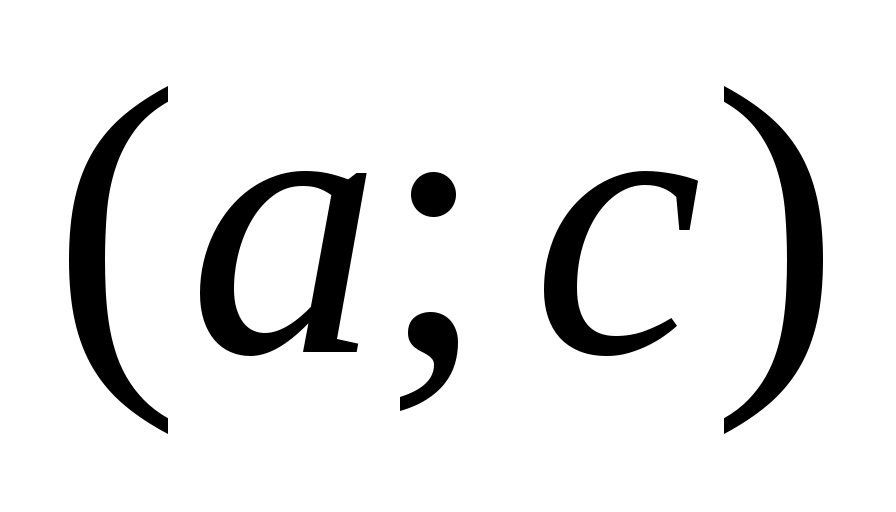 и и 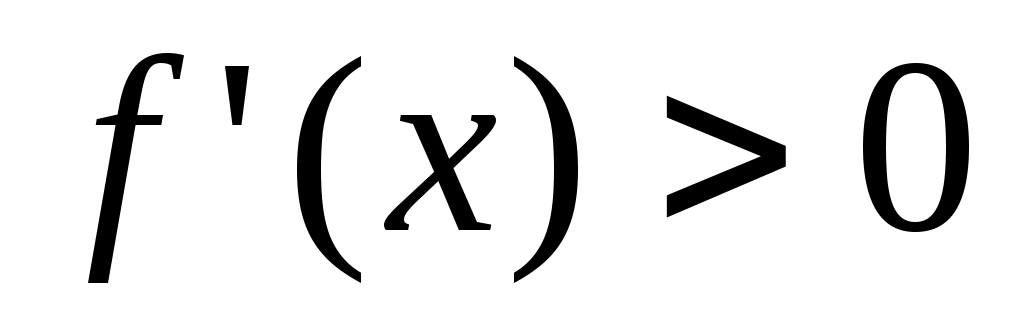 на на 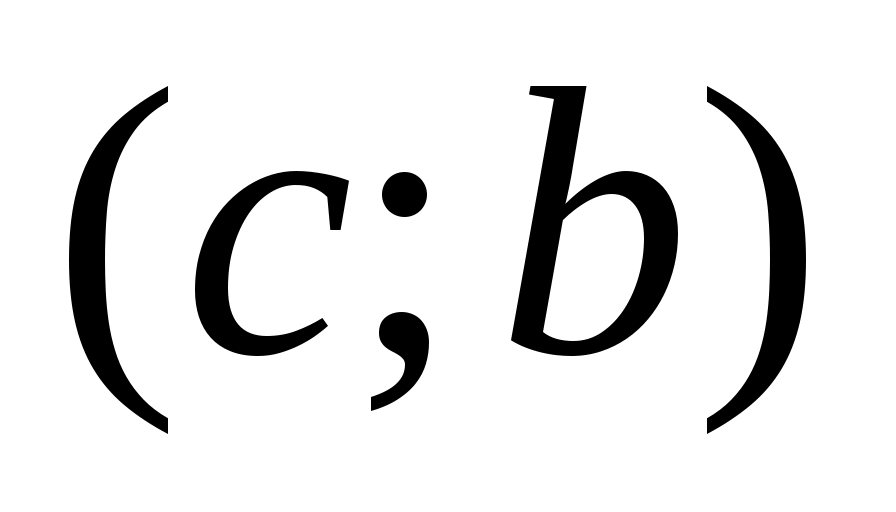 . Тогда при любом х из . Тогда при любом х из 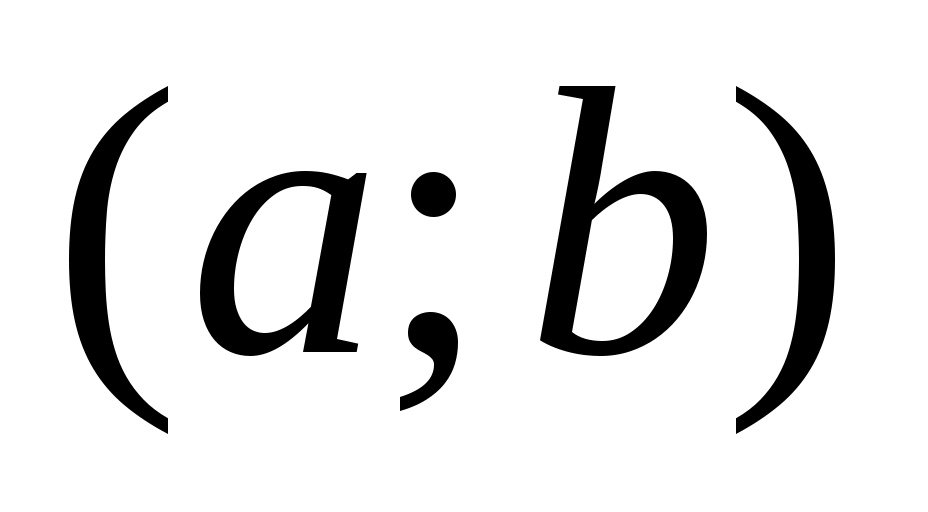 справедливо неравенство справедливо неравенство 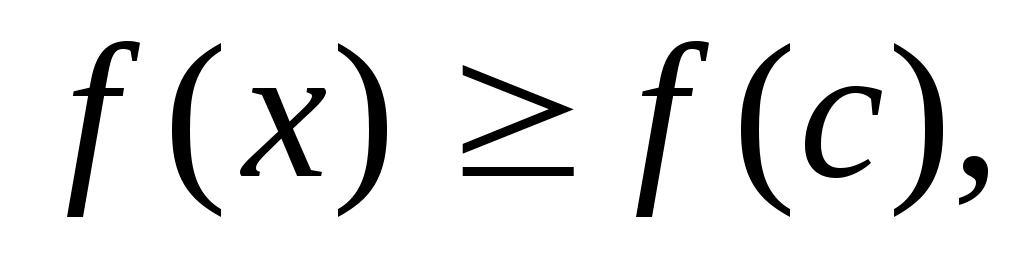 причем равенство имеет место лишь при причем равенство имеет место лишь при 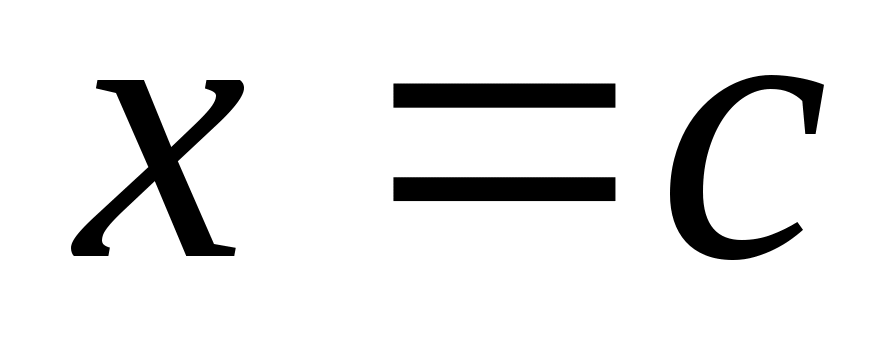 . .
Задача 8. Проверьте, справедливо ли для всех действительных х следующее неравенство: 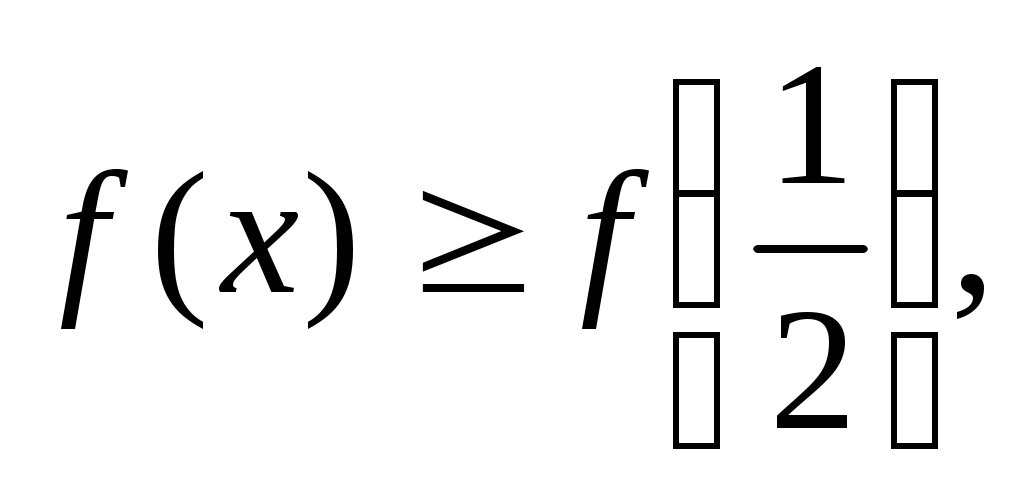 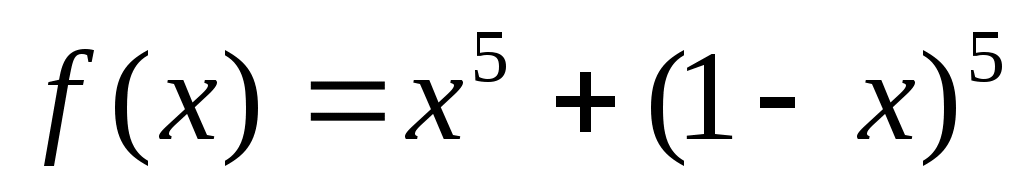
Решение: Выясним, где функция возрастает, а где убывает. Для этого найдем производную:
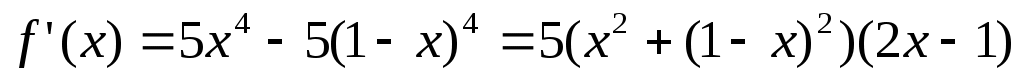 . .
Видно, что 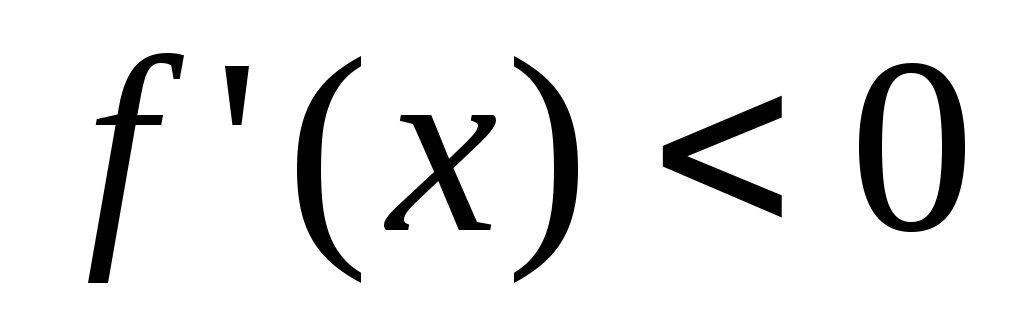 на на 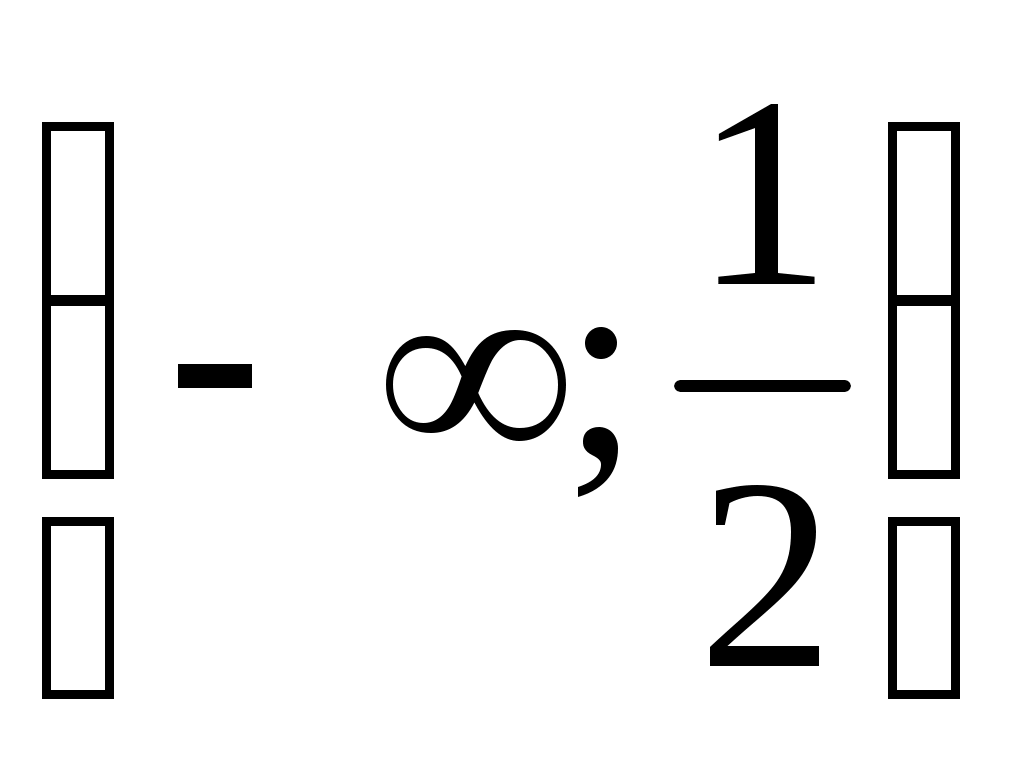 и и 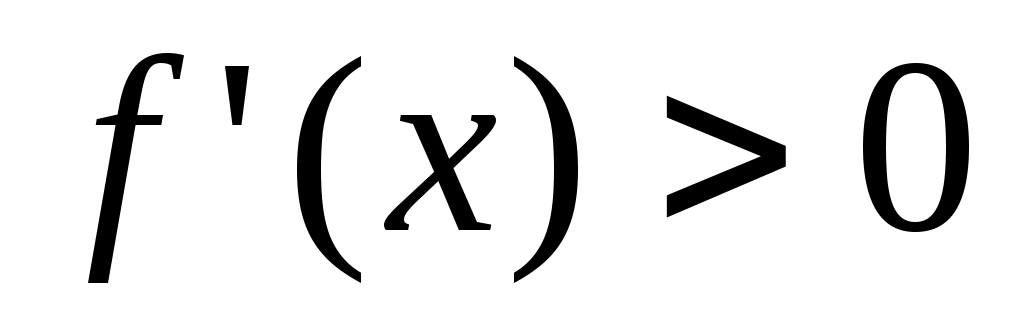 на на 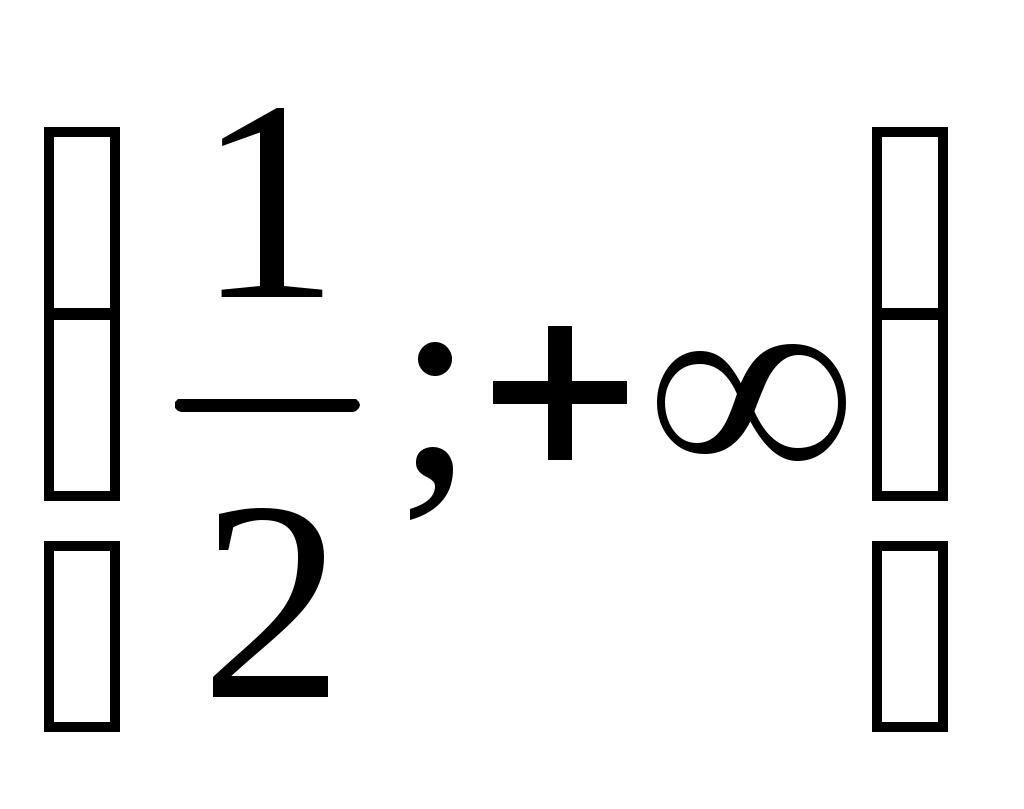 . Следовательно, в силу теоремы 3 т.е. неравенство (9) справедливо, причем равенство имеет место лишь при . Следовательно, в силу теоремы 3 т.е. неравенство (9) справедливо, причем равенство имеет место лишь при 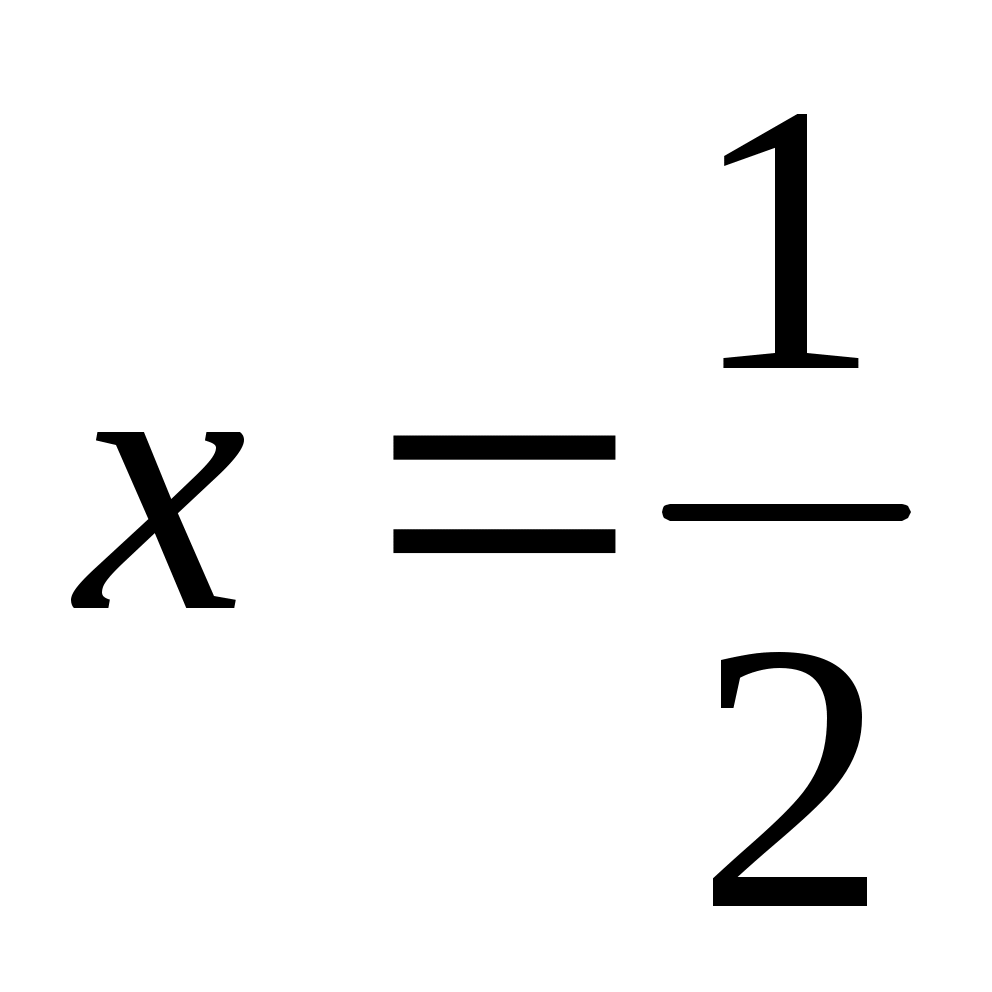 . .
|
|
|
 Скачать 1.6 Mb.
Скачать 1.6 Mb.