Математика. Реферат Производная и ее приложения ученик 11А класса Новиков А. Проверила Шекера Г. В. г. Хабаровск
 Скачать 1.6 Mb.
|
9.2. Применение производной в доказательстве тождеств.Доказательства тождества можно достигнуть иногда, если воспользоваться одним очевидным замечанием: Если на некотором интервале функция тождественно равна постоянной, то ее производная на этом интервале постоянно равна нулю:  на  на  . Задача 1. Проверить тождество:  (1)Доказательство: Рассмотрим функцию  Вычислим ее производную (по х):  Поэтому (замечание)  . Следовательно,  что равносильно тождеству (1).Задача 2. Проверить тождество:  (2)Доказательство: Рассмотрим функцию  Докажем, что  Найдем ее производную:     Значит . При х=0  ,следовательно,тождество (2) верно.В связи с рассмотренными примерами можно отметить, что при нахождении постоянной, интегрирования С полезно фиксировать значения переменной, по которой производится дифференцирование, таким образом, чтобы получить возможно более простые выкладки. 9.3. Применение производной для упрощения алгебраических и тригонометрических выражений.Прием использования производной для преобразования алгебраических и тригонометрических выражений основан на том, производная иногда имеет значительно более простой вид, чем исходная функция, благодаря чему, она легко интегрируется, что и позволяет найти искомое преобразование исходного выражения: Задача 1 Упростить выражение:  Решение: Обозначив данное выражение  будем иметь:    Таким образом, заданное выражение (1) равно  . Задача 2. Упростить выражение:  Решение: Обозначив это выражение через 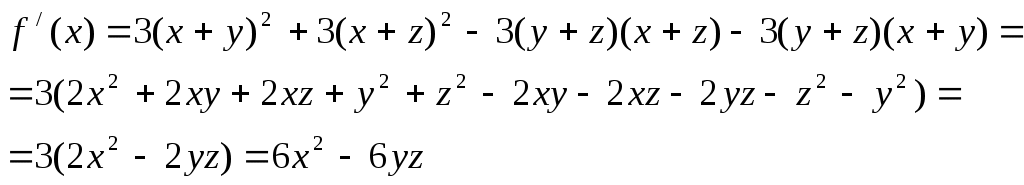 , будем иметь:  отсюда  . и при  получаем:  Так что  Задача 3. Упростить запись функции:  (2)Решение: Применение обычного аппарата тригонометрии приведёт к относительно громоздким выкладкам. Здесь удобнее воспользоваться производной:  Отсюда  Найдём  :  Таким образом функция (2) равна  Задача 4. Упростить запись многочлена:  (3)Решение: Обозначим многочлен (3) через  и найдём последовательно первую и вторую производные этой функции:  Ясно, что  Поэтому  , где  , найдём  : при  ,  . |