Математика. Реферат Производная и ее приложения ученик 11А класса Новиков А. Проверила Шекера Г. В. г. Хабаровск
 Скачать 1.6 Mb.
|
4. Правила дифференцирования
    Производная степенно-показательной функции  , где  . .Логарифмическое дифференцирование. Пусть дана функция  . При этом предполагается, что функция  не обращается в нуль в точке  . Покажем один из способов нахождения производной функции  , если  очень сложная функция и по обычным правилам дифференцирования найти производную затруднительно.Так как по первоначальному предположению не равна нулю в точке, где ищется ее производная, то найдем новую функцию  и вычислим ее производную (1)Отношение  называется логарифмической производной функции . Из формулы (1) получаем . Или  Формула (2) дает простой способ нахождения производной функции .5. Производные высших порядковЯсно, что производная  функции y =f (x) есть также функция от x:  Если функция f ' (x) дифференцируема, то её производная обозначается символом y'' =f '' (x) и называется второй производной функции f(x) или производной функции f(x) второго порядка. Пользуясь обозначением 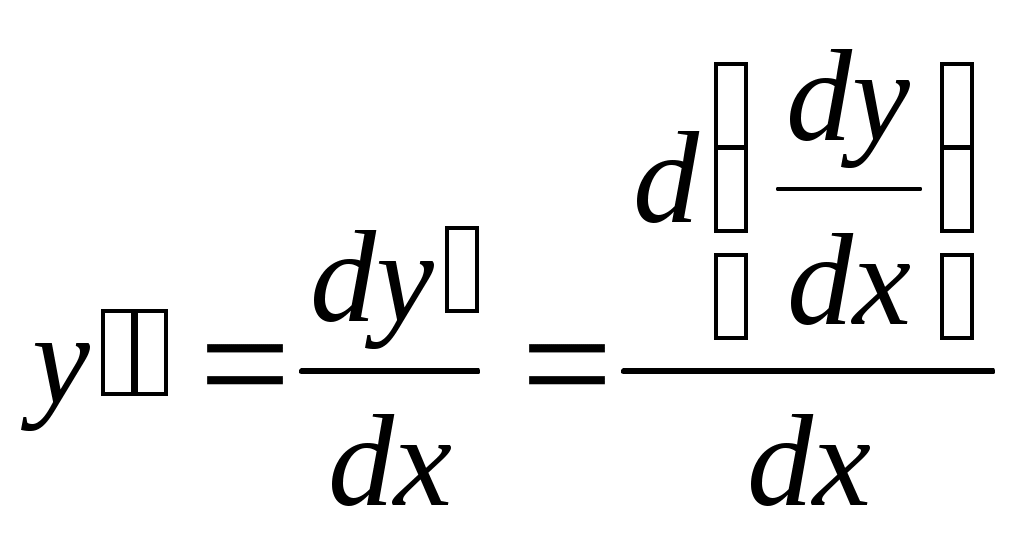 можем написать  Очень удобно пользоваться также обозначением  , указывающим, что функция y=f(x) была продифференцирована по x два раза.Производная второй производной, т.е. функции y''=f '' (x) , называется третьей производной функции y=f(x) или производной функции f(x) третьего порядка и обозначается символами  .Вообще n-я производная или производная n-го порядка функции y=f(x) обозначается символами  Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д. Тогда возникает вопрос: сколько производных высших порядков можно получить в случае произвольной функции. Например: 1)  ;  ;  ; ...;  ;  .Разные функции ведут себя по-разному при многократном дифференцировании. Одни имеют конечное количество производных высших порядков, другие – переходят сами в себя, а третьи, хотя и дифференцируемы бесконечное количество раз, но порождают новые функции, отличные от исходной. Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков. |
