Зинаида. МУ им. Витте, БУ и А - 2 (рейтинговая работа), в-Ж-З (копия). Рейтинговая работа
 Скачать 87.04 Kb. Скачать 87.04 Kb.
|
|
Решение: Расчёт влияния факторов в четырёхфакторной мультипликативной модели проведем методом цепных постановок в таблице 4 Таблица 4 – Расчёт влияния факторов в четырёхфакторной мультипликативной модели методом цепных подстановок
Как видно из данных таблицы, стоимость выпущенной продукции в отчётном году уменьшилась по сравнению с базисным на 121 тыс. руб., что составляет 1,5%. Второй показатель объёма продукции (ВПусл.1) отличается от первого (ВП0) тем, что при его расчёте принята фактическая численность рабочих отчётного периода вместо базисного. Все остальные факторы (количество отработанных дней одним рабочим за год; средняя продолжительность смены; среднечасовая выработка одного рабочего) и в том и другом случае базисные. Значит, за счёт уменьшения количества рабочих в отчётном периоде на 3 человека объём продукции снизился на 1896 тыс. руб. (6321-8217). Третий показатель (ВПусл.2) отличается от второго (ВПусл.1) тем, что при его расчёте вместо базисной величины количества отработанных дней одним рабочим за год используется его величина в отчётном периоде. Остальные факторы (средняя продолжительность смены; среднечасовая выработка одного рабочего) продолжают оставаться базисными. Количество рабочих в обоих случаях отчётного периода. Отсюда, за счёт уменьшения количества отработанных дней одним рабочим на 5 дней объём продукции снизился на 123 тыс. руб. (6199-6321). Четвёртый показатель (ВПусл.3) отличается от третьего (ВПусл.2) тем, что при расчёте его величины вместо базисной величины продолжительности рабочего дня используется его величина в отчётном периоде. При этом среднечасовая выработка остаётся базисной. Количество рабочих и количество отработанных дней одним рабочим за год в обоих случаях отчётного периода. Значит, за счёт того, что средняя продолжительность смены увеличилась на 1 час объем продукции увеличился на 886 тыс. руб. (7084-6199). Пятый показатель (ВП1) отличается от четвёртого (ВПусл.3) тем, что при расчёте его величины вместо базисной величины выработки используется его величина в отчётном периоде. Количество рабочих , количество отработанных дней одним рабочим за год, а также средняя продолжительность рабочего дня в обоих случаях отчётного периода. Отсюда за счёт роста производительности труда на 50 руб. объём продукции вырос на 1012 тыс. руб. (8096-7084). Таким образом, увеличение выпущенной продукции явилось результатом следующих факторов: Увеличения численности рабочих………………………………-1896 тыс. руб. Увеличения количества отработанных дней одним рабочим…-123тыс. руб. Сокращения средней продолжительности рабочего дня…..……+886 тыс. руб. Увеличения среднечасовой выработки………………….………+1012 тыс. руб. Итого -121 тыс. руб. Алгебраическая сумма влияния факторов должна быть равна общему изменению результативного показателя: ΔВПчр + ΔВПд + ΔВПп + ΔВПчв = ΔВПобщ Отсутствие такого равенства свидетельствует о допущенных ошибках в расчётах. Методика детерминированного факторного анализа способ абсолютных разниц Преобразование основного алгоритма метода цепных подстановок позволяет делать Расчёт влияния факторов в мультипликативной четырёхфакторной модели ВП = ЧР * Д * П * ЧВ методом абсолютных разниц приведён в таблице 5. Таблица 5 – Расчёт влияния факторов методом абсолютных разниц в мультпликативной модели
Задание 3 Условие: Используя данные 10-ти предприятий (данные необходимо брать из пункта 3), произведите стохастический факторный анализ (корреляционный анализ). В качестве примера прямолинейной зависимости между факторным и результативным показателем используйте данные об изменении уровня выработки рабочих (Y) в зависимости от уровня фондовооружённости труда (X), представленные в таблице.
Решение: В качестве прямолинейной зависимости между факторным и результативным показателем используем данные об изменении уровня выработки рабочих (Y) в зависимости от уровня фондовооружённости труда (х), представленные в таблице 6. Таблица 6 – Зависимость выработки рабочих (Y) от фондовооружённости труда (X)
В таблице 6 приведены ранжированные данные о выработке рабочих и фондовооружённости труда по 10 предприятиям одной и той же отрасли. По приведённым в таблице данным видно, что связь между исследуемыми показателями носит прямолинейный характер, так как показатели изменяются в одном направлении: при повышении уровня фондовооруженности труда производительность труда рабочих также возрастает. Подставим показатели из нашего примера в приведённую выше систему уравнения: 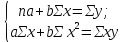 где n – число наблюдения (в нашем примере – это 10 предприятий отрасли); х – фондовооруженность труда, тыс. руб. y – среднегодовая выработка продукции одним работником, тыс. руб. Значения Σх, Σу, Σх2, Σху рассчитываются на основании фактических исходных данных; результаты расчётов представлены в таблице 7. Таблица 7 – Расчёт производных данных для корреляционного анализа
Подставив полученные значения в систему уравнений, получим: 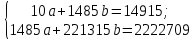 Умножим все члены первого уравнения на 148,5: 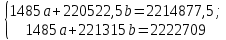 Затем из второго уравнения вычтем первое и определим показатели a и b: 792,5b = 7831,5. Отсюда b = 7831,5 / 792,5 = 9,882 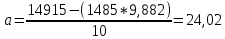 Уравнение связи, описывающее зависимость производительности труда от его фондовооружённости, имеет выражение: Yx = 24,05 + 9,882x. Коэффициент а (в нашем случае этот коэффициент равен 24,02) является постоянной величиной, не связанной с изменением факторного показателя. Коэффициент b показывает, как изменяется результативный показатель с изменением данного факторана единицу его измерения. В приведённом примере это означает, что если фондовооруженность труда рабочих основными средствами возрастает на 1 тыс. руб., то их выработка увеличивается в среднем на 9,882 тыс. руб. Если в уравнение регрессии Yx = 24,02 + 9,882x соответствующее значение х, то можно рассчитать выравненное значение производительности труда (Yx) для каждого предприятия и оценить работу каждого из них. Например, выработка рабочих на первом предприятии будет составлять: Yx = 24,02 + 9,882 * 134 = 1348 Полученная величина 1348 показывает выработку рабочих при фондовооруженности 134 при условии использования данным предприятием своих производственных мощностей как в среднем все анализируемые предприятия данной отрасли. Как видно из данных таблицы, фактическая выработка на первом предприятии составляет 1348 тыс. руб., что выше расчётного значения. Это означает, что на данном предприятии производственные мощности используются лучше, чем в среднем по отрасли. Аналогичные расчёты сделаны для каждого предприятия, и данные по ним приведены в последней колонке таблицы 7. Таким образом, регрессионный анализ даёт возможность определить степень зависимости между факторным и результативным показателем. Однако он не позволяет определить, насколько эта связь тесна. Для измерения тесноты связи между результативным и факторным показателем используется коэффициент корреляции,который при прямолинейной форме связи между исследуемыми показателями рассчитывается по формуле: 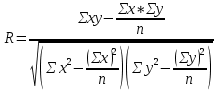 Коэффициент корреляции может принимать значения от 0 до 1. Чем ближе его величина к 1, тем более тесная существует связь между факторным и результативным показателем. Рассчитаем коэффициент корреляции, подставив в данную формулу значения Σх, Σу, Σх2, Σху, Σy2 из таблицы 7. 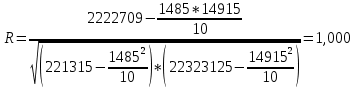 В нашем примере коэффициент корреляции (R) равен 1,000. Он равен единице, что свидетельствует о тесной связи между фондовооруженностью и производительностью труда на анализируемых предприятиях. Коэффициент корреляции позволяет также сделать вывод, что одним из основных факторов роста производительности труда на данных предприятиях является рост фондовооруженности труда. Коэффициент корреляции, возведённый в квадрат (1,02) даёт показатель коэффициента детерминации, показывающий долю фондовооруженности труда в изменении показателя производительности труда. В нашем примере коэффициент детерминации, составляющий 100% , показывает, что производительность труда на 100% зависит от фондовооруженности труда, в то время как на долю остальных факторов приходится 0% изменения её уровня. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
