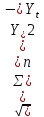Зинаида. МУ им. Витте, БУ и А - 2 (рейтинговая работа), в-Ж-З (копия). Рейтинговая работа
 Скачать 87.04 Kb.
|
 Кафедра бухгалтерского учета, налогообложения и таможенного дела Рейтинговая работа _______________________________________________ (расчетно-аналитическое задание) по дисциплине _________________________________________________ Задание/вариант № Ж-З Выполнена обучающимся группы __________________________________ __________________________________________________________________ (фамилия, имя, отчество) Преподаватель ___________________________________________________ (фамилия, имя, отчество) Москва – 2019 г. Содержание Задание 1…………………………………………………………….…………….3 Задание 2…………………………………………………………………………..8 Задание 3…………………………………………………………………………12 Задание 4…………………………………………………………………………16 Список использованных источников…………………………………………...21 Задание 1 Условие: Используя ретроспективные данные за 6 лет, спрогнозируйте объем производства продукции на следующие 3 года при условии сохранения тенденций функционирования бизнеса. Таблица 1 – Исходные данные для трендового анализа
Решение: Используя ретроспективные данные предприятия за 6 лет, представленные в таблице 1, спрогнозируем объёмы производства продукции на следующие 3 года при условии сохранения среды функционирования бизнеса (таблица 2). Таблица 2 – Исходные данные для трендового анализа
Расчёт среднего объёма производства продукции показывает, что в каждый период (квартал) предприятие производило в среднем 26,0 условных единицы продукции. Значение объёма производства в динамике увеличивается. Зависимость между объёмом производства продукции и периодом времени показана на рисунке 1. 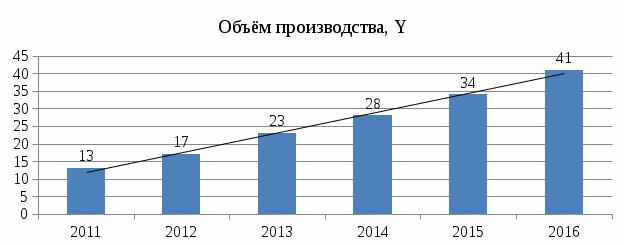 Рисунок 1. – Динамика производства продукции Если связь между факторным и результативным показателями носит прямолинейный характер, то уравнения парной регрессии имеют вид: Yt = a + b*x где а – свободный член уравнения при член уравнения при х = 0 x – фактор, определяющие уровень изучаемого результативного показателя (независимый параметр); b – коэффициент регрессии при факторном показателе; он характеризуют уровень влияния фактора на результативный показатель в абсолютном выражении. Показатели а и b следует отыскать. Значение коэффициентов a и b находят из системы уравнений, полученных по способу наименьших квадратов (x = t): 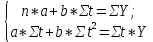 где n – число наблюдения (в нашем примере – это 10 кварталов); t – независимый параметр Y – объём производства продукции. Значения Σt, ΣY, Σt2, ΣtY рассчитываются на основании фактических исходных данных; результаты расчётов представлены в таблице 3. Таблица 3 – Расчёт показателей трендовой модели для прогноза объёма производства продукции
Подставив полученные значения в систему уравнений, получим: 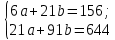 Умножим все члены первого уравнения на 21, а члены второго уравнения на 6, получим систему уравнений: 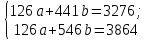 Затем из второго уравнения вычтем первое и определим показатели a и b: 0 *a + 105 * b = 588, отсюда b = 588 / 105 = 5,6 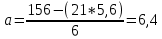 Уравнение связи для определения объёма производства в зависимости от периода времени при заданных данных имеет выражение: Yx = 29,2 + 4,8*t. Если в уравнение регрессии Yx = 6,4 + 5,6 * t подставить соответствующее значение t, то можно рассчитать прогнозируемое значение объёма производства (Yx) для каждого ретроспективного квартала и последующего квартала (столбец 6). Y1 = 6,4 + 5,6 * 1 = 13 ед. Y2 = 6,4 + 5,6 * 2 = 17 ед. ………………………………….. Y7 = 6,4 + 5,6 * 7 = 46 ед. Y8 = 6,4 + 5,6 * 8 = 51 ед. Y9 = 6,4 + 5,6 * 9 = 57 ед. В колонках 7, 8 рассчитаны отклонения фактического уровня производства продукции от расчётного для каждого ретроспективного и прогнозного периода. Для оценки качества данных, определения диапазона изменения прогнозируемого объёма производства в каждый квартал рассчитаем среднее квадратическое отклонение прогнозируемого показателя и коэффициент вариации по формулам: Среднеквадратическое отклонение: δ = 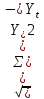 коэффициент вариации: 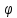 =  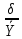*100%.В таблице 3 показаны алгоритм и результаты расчётов этих показателей. В нашем примере среднеквадратическое отклонение составило 0,7 единиц. С учётом этого показателя можно указан прогнозируемый диапазон изменения объёма производства для каждого из трех лет, начиная с 7-го. Результаты расчётов показали, что прогнозируемый диапазон объёма производства составит: для 2017-го года – от 45 ед. до 46 ед.; для 2018-го года – от 50 ед. до 52 ед.; для 2019-го года – от 56 ед. до 58 ед. Коэффициент вариации показывает, на сколько % в среднем отклоняется величина Y от своего среднего значения математического ожидания. Чем выше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Если вариация не больше 10%, то изменчивость вариационного ряда незначительна. Если вариация составляет 10-12% изменчивость вариационного ряда считается средней. Изменчивость вариационного ряда является значительной, если вариация больше 20%, но не превышает 33%. Превышение вариации 33% указывает на неоднородность информации и необходимость исключения нетипичных наблюдений. Значение коэффициента вариации в нашем примере составило 2,8%, что означает слабую колеблемость анализируемого признака. Так как разброс значений вокруг среднего незначительный, риск бизнеса производства продукции низкий. Задание 2 Условие: Используя данные из пункта 3 произвести факторный анализ следующих факторных детерминированных моделей. 1. Произвести расчет влияния факторов в четырёхфакторной мультипликативной модели ВП = ЧР * Д * П * ЧВ методом цепных постановок. Таблица – Расчёт влияния факторов в четырёхфакторной мультипликативной модели методом цепных подстановок
2. Произвести расчет влияния факторов в мультипликативной четырёхфакторной модели ВП = ЧР * Д * П * ЧВ методом абсолютных разниц. Таблица – Расчёт влияния факторов методом абсолютных разниц в мультпликативной модели
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
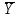= ΣYt / n