лАБ111. Рекурсивные алгоритмы. Оценка сложности алгоритмов

• Название: Рекурсивные алгоритмы. Оценка сложности алгоритмов
• Анкор: лАБ111
• Дата: 27.02.2022
• Размер: 5.12 Mb.
• Имя файла: Laba_yap_11 (10).docx
• Тип: Отчет; #375706

Министерство образования Республики Беларусь

Белорусский Национальный Технический Университет
Факультет информационных технологий и робототехники
Кафедра «Программное обеспечение информационных систем

и технологий»


Отчёт

по лабораторной работе №22

по дисциплине «Языки программирования»

тема: «Рекурсивные алгоритмы. Оценка сложности алгоритмов»

Исполнитель:		студентка группы 10702120 Рахман С.М. Дарья Каблур
Преподаватель:		Лапанович Ирина Олеговна

2020-2021 учебный год
ЛАБОРАТОРНАЯ РАБОТА №22
Рекурсивные алгоритмы. Оценка сложности алгоритмов.
Цель работы:

Изучить и освоить рекурсивный способ решения итерационного характера задачи; научиться грамотно проектировать и декомпозировать (разбивать) задачи на более мелкие фрагменты с использованием рекурсивных алгоритмов и практически закрепить полученные знания на примере разработки интерактивных приложений.

Общее задание:

Для решения каждой задачи нужно представить минимум две реализации: одна – на базе циклов, а другая – на базе рекурсии.

1. 
   Опишите функцию, которая вычисляет сумму цифр заданного числа.
   
2. 
   Требуется описать функцию, которая бы определяла, является ли заданное число точной степенью двойки (или тройки и т.д.). Если не является, то функция должна возвращать -1.
   
3. 
   Необходимо описать функцию power(x, n), вычисляющую xⁿ для любого вещественного x(≠0) и любого целого n. Предусмотреть два рекурсивных алгоритма реализации: простой алгоритм нахождения степени числа и ускоренный. Оценить с использованием Big O алгоритмическую сложность данных вариантов.
   
4. 
   Рекурсивно описать функцию max_digit(N), которая находит наибольшую цифру в десятичной записи неотрицательного целого числа N. Например, max_digit(27306) = 7 или max_digit(829374) = 9.
   
5. 
   Необходимо реализовать функцию, которая вычисляет N-элемент ряда Фибоначчи. На базе данной функции разработать программу, которая должна предлагать пользователю следующие возможности: вывод конкретного элемента последовательности; вывод всех элементов последовательности до указанного пользователем элемента; или той части последовательности, значение последнего элемента которой не превосходит введённое пользователем значение).
   

6. 
   Требуется описать функцию f(x, n), вычисляющую величину xⁿ/n! при любом вещественном x и любом неотрицательном целом n.
   
7. 
   Описать рекурсивную функцию equals(N, S) (где N и S – неотрицательные целые числа), которая про
   
8. 
   Проверяет, совпадает ли сумма цифр в десятичной записи числа N со значением S (например: equals(1234567, 28) = True, equals(10, 7) = False, equals(10000, 1) = True и т.д.).
   
9. 
   Рекурсивно описать функцию divs(N) для подсчета количества всех делителей целого числа N (N > 1), без учета делителей 1 и N (например: divs(7) = 0, divs(10) = 2, divs(16) = 3 и т.д.).
   
10. 
    Опишите функцию, которая вычисляет сумму элементов заданной одномерной последовательности.
    
11. 
    Опишите функцию, которая реверсирует элементы заданной одномерной последовательности.
    

Дополнительное задание:

1. 
   Напечатать N автоморфных чисел(автоморфнымн азывается число,совпадающее с младшими цифрами своего квадрата, например: 25 и 625).
   

2. 
   Найти N троек чисел Пифагора (натуральные числа a, b и c называются числами Пифагора, если выполняется условие a² + b² = c²).
   
3. 
   Задача о Ханойской башне (Tower of Hanoi)
   

Имеется три стержня, на один из которых
нанизаны N колец, причем кольца отличаются
размером и лежат меньшее на большем. Требуется перенести пирамиду из N колец с одного стержня на другой за наименьшее число ходов. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее.

Например, для функции Hanoi (3,'A','B', 'C'), где 3 – число колец, A – имя стержня - источника, B – имя стержня-приемника, C – имя временного стержня, должен получиться такой ответ: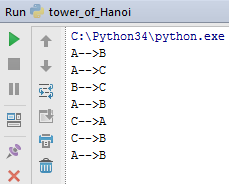

4. 
   Найти все натуральные числа, не превосходящие N, сумма цифр каждого из которых в некоторой степени дает это число (например: 7⁴ = 2 401, 8³ = 512, 9² = 81 или 18³ = 5 832, 18⁶ = 34 012 224, 18⁷ = 612 220 032 и т.д.).
   
5. 
   Необходимо написать программу, которая определяет, состоит ли строка только из английских букв и соответствующих пробельных символов и знаков препинания.
   

Для тех, кто хочет закрепить свои знания и навыки для решения задач с помо-щью рекурсий, рекомендую также зайти сюда: http://server.179.ru/tasks/ training/recursion.html, а также сюда: https://ru.wikibooks.org/wiki/Рекурсия.
Требования к выполнению:

1. 
   Необходимо спроектировать блок-схемы алгоритмов решений соответствующих заданий и на базе данных алгоритмов разработать интерактивные консольные приложения с использованием архитектурного шаблона проектирования MVC и модулей языка Python.
   
2. 
   Вычислительные алгоритмы должны быть простыми и эффективными!
   
3. 
   Для каждого алгоритма решения задания (которые реализуются с помощью циклов и с помощью рекурсий) оценить (вычислить) алгоритмическую сложность по необходимому времени и затрачиваемой памяти используя определение Big O.
   
4. 
   Для масштабируемости разрабатываемого программного решения размер последовательности (списка) и его элементы должны задаваться пользователем во время выполнения программы или с помощью генератора псевдослучайных чисел.
   
5. 
   Для автоматизации заполнения различными значениями искомого контейнера рекомендуется использовать соответствующие функции генерирования псевдослучайных чисел модуля random.
   
6. 
   Рекомендуется избегать использования глобальных переменных при написании основной логики приложения.
   
7. 
   Если логически не подразумевается или в заданиях иного не указано, то входными и выходными данными являются вещественные числа (числа с плавающей запятой).
   

8. 
   Все программы должны быть разбиты на отдельные функции. Среди данных функций рекомендуется добавлять стартовую функцию main, с которой лучше производить запуск программы.
   
9. 
   При выполнении заданий необходимо по максимуму пытаться разрабатывать универсальный, масштабируемый, легко поддерживаемый и читаемый код.
   
10. 
    Также рекомендуется придерживаться Single Responsibility Principle, SRP (принципа единственной ответственности) – постарайтесь вынести основную бизнес-логику задания в отдельную функцию (т.е. архитектура приложения должна минимум состоять из нескольких функций).
    
11. 
    В соответствующих компонентах (функциях) бизнес-логики необходимо предусмотреть «защиту от дурака».
    
12. 
    При проверке работоспособности приложений необходимо проверить все тестовые случаи.
    
13. 
    Программы должны обязательно быть снабжены комментариями на английском языке, в которых необходимо указать краткое предназначение программ, номер лабораторной работы и её название, версию программы, ФИО разработчика, название бригады (если есть), номер группы и дату разработки. Исходный текст программного кода и демонстрационной программы рекомендуется также снабжать поясняющими краткими комментариями.
    
14. 
    Программы должны быть снабжены дружелюбным и интуитивно понятным интерфейсом для взаимодействия с пользователем. Интерфейс программ должен быть на английском языке.
    
15. 
    При разработке программ придерживайтесь соглашений по написанию кода на Python (Python Code Convention).
    

Результаты выполнения общего задания:




Рисунок 1 - Результат выполнения интерактивной программы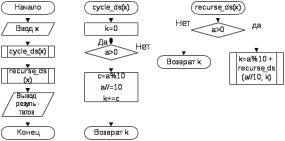



Блок-схема 1 (общее задание)

Алгоритмическая сложность по количеству операций: циклический алгоритм -- O(N), рекурсивный алгоритм – O(N), по объему затрачиваемой памяти: циклический алгоритм – const, рекурсивный алгоритм – 2N.

Р 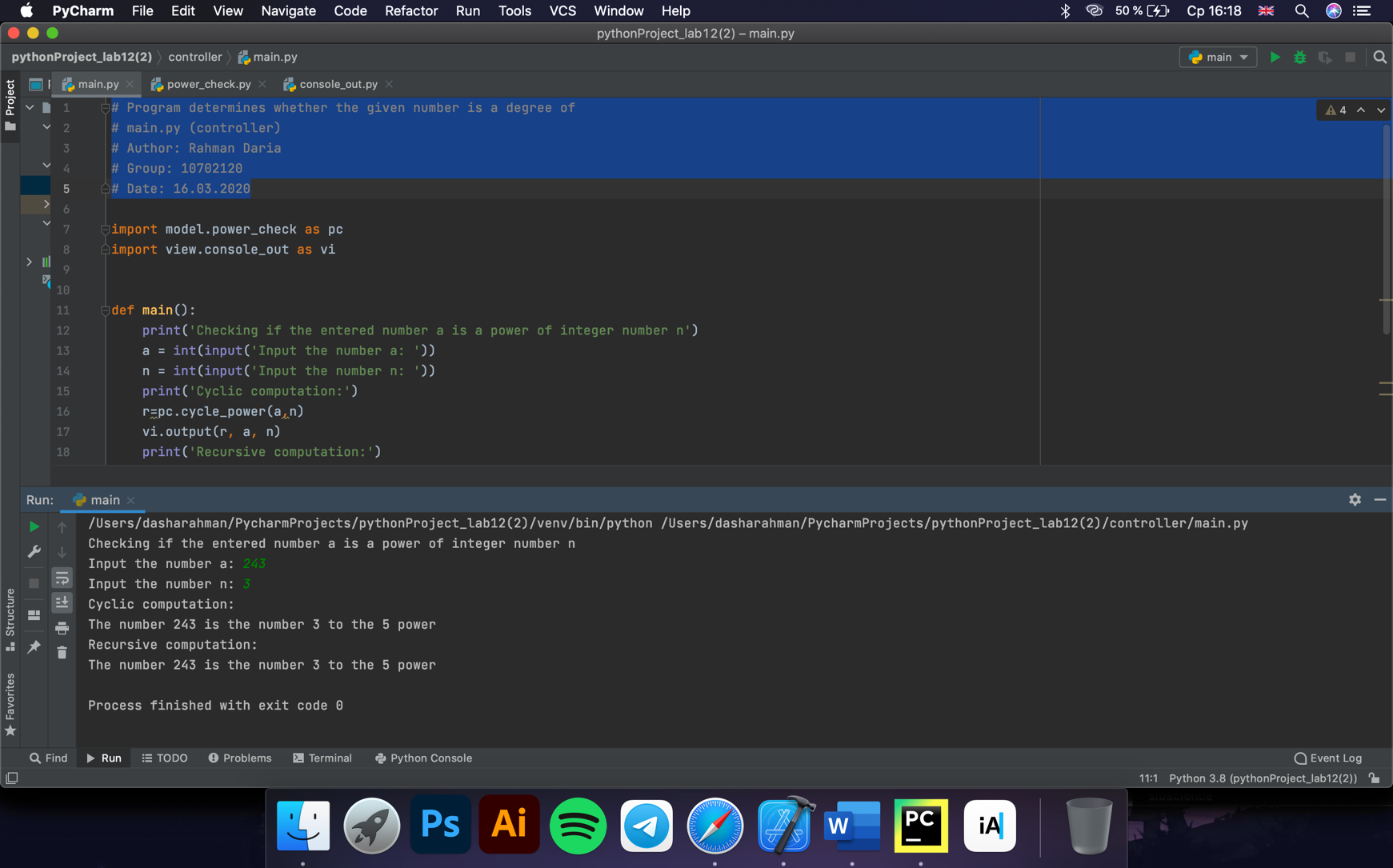исунок 2 - Результат выполнения интерактивной программы


Блок-схема 2 (общее задание)

Алгоритмическая сложность по количеству операций: циклический алгоритм – O(N), рекурсивный алгоритм – O(N), по объему затрачиваемой памяти: циклический алгоритм – const, рекурсивный алгоритм – 2N.



Рисунок 3 - Результат выполнения интерактивной программы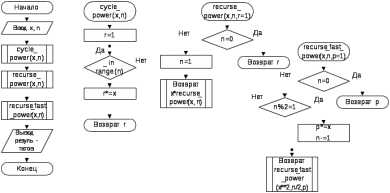



Блок-схема 3 (общее задание)

Алгоритмическая сложность по количеству операций: циклический алгоритм – O(N), рекурсивный алгоритм – O(N), рекурсивный ускоренный алгоритм – O(log(N)), по объему затрачиваемой памяти: циклический алгоритм – const, рекурсивный алгоритм – 2N, рекурсивный ускоренный алгоритм – 2log(N).



Рисунок 4 - Результат выполнения интерактивной программы



Блок-схема 4 (общее задание)

Алгоритмическая сложность по количеству операций: циклический алгоритм – O(N), рекурсивный алгоритм – O(N), по объему затрачиваемой памяти: циклический алгоритм – const, рекурсивный алгоритм – 2N.



Рисунок 5 - Результат выполнения интерактивной программы


Блок-схема 5 (общее задание)

Алгоритмическая сложность по количеству операций: циклический алгоритм – O(N), рекурсивный алгоритм – O(2^N), по объему затрачиваемой памяти: циклический алгоритм – const, рекурсивный алгоритм – 2^N.

Р исунок 6 - Результат выполнения интерактивной программы

Рисунок 7 - Результат выполнения интерактивной программы



Рисунок 8 - Результат выполнения интерактивной программы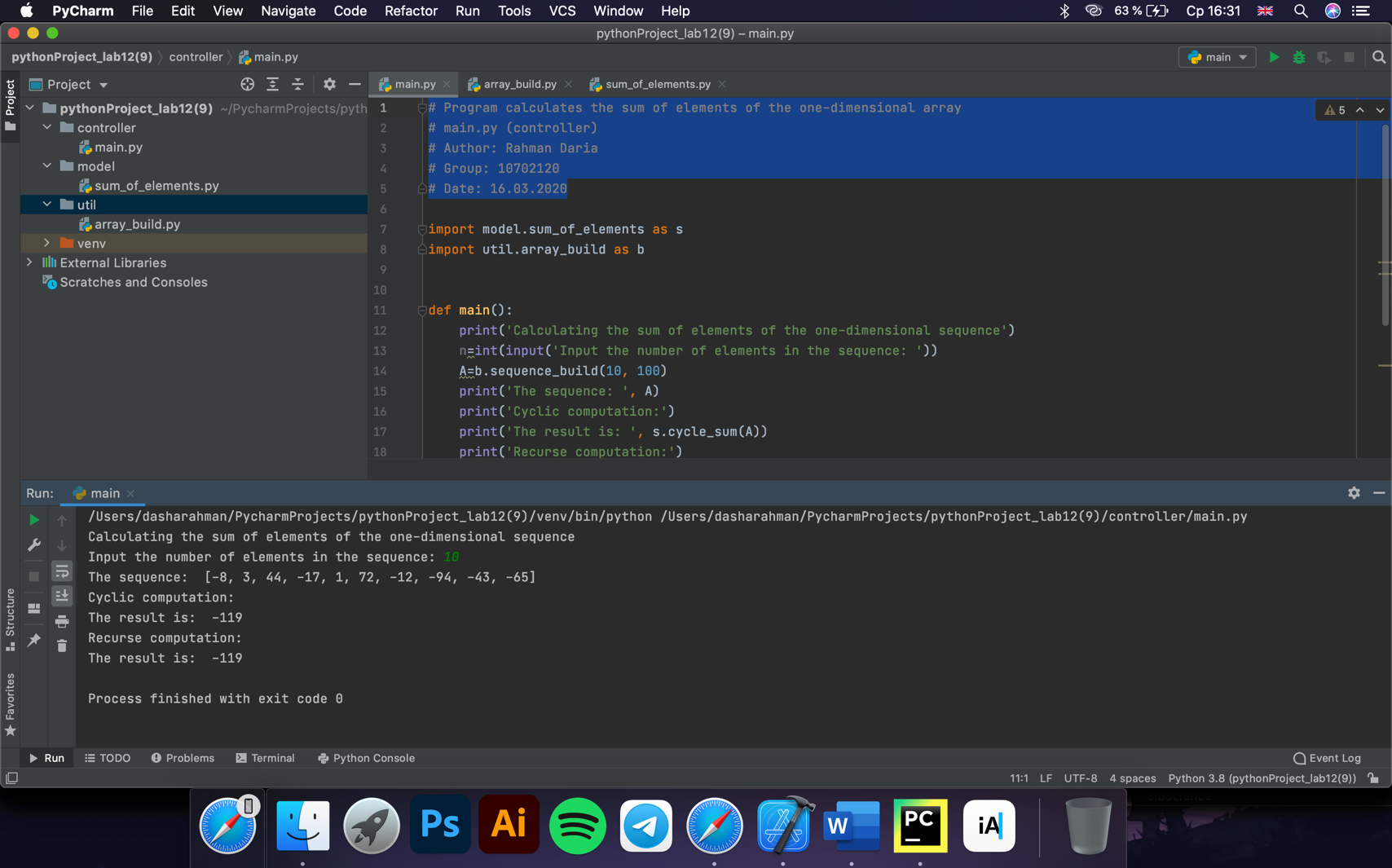




Рисунок 9 - Результат выполнения интерактивной программы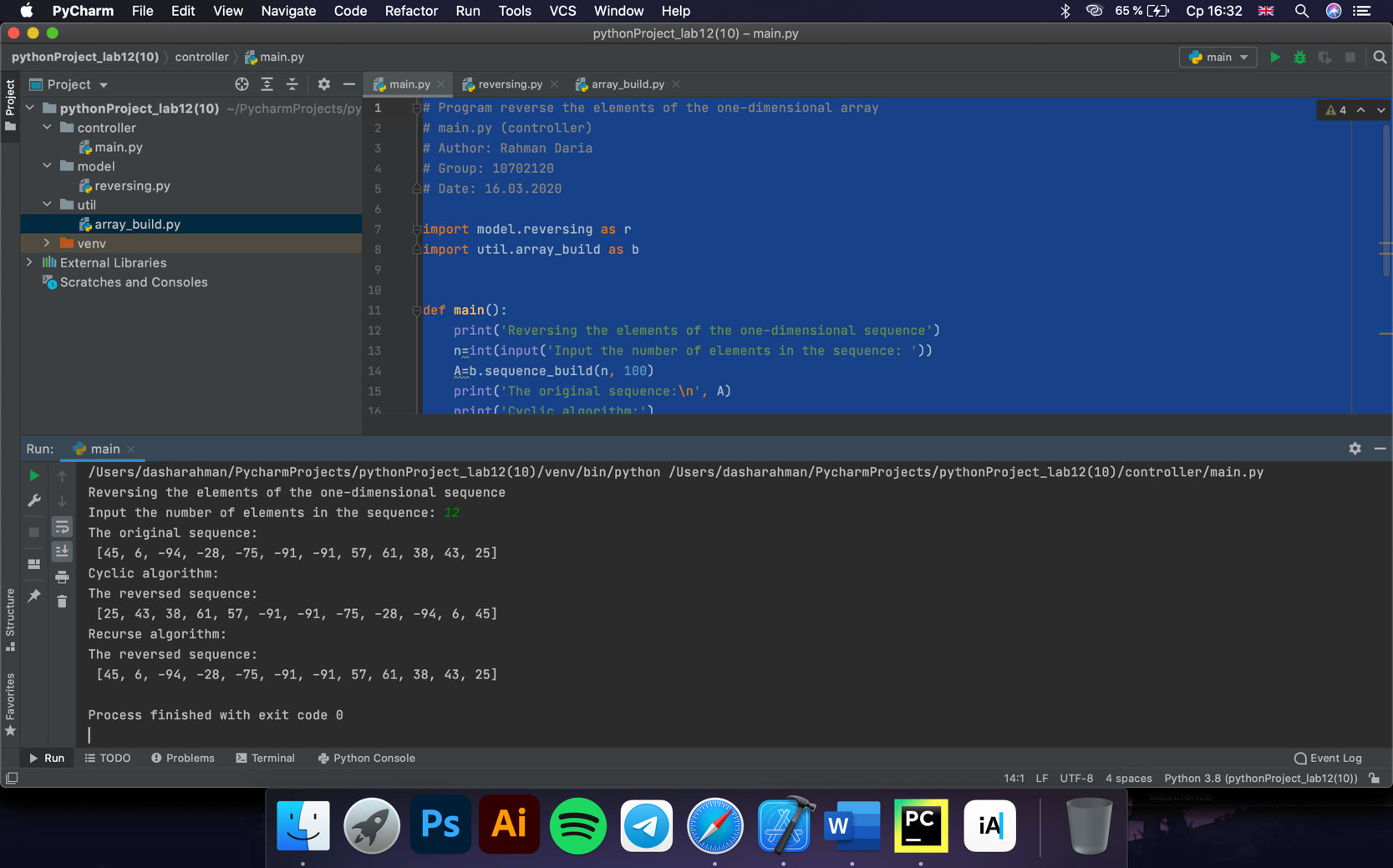




Рисунок 10 - Результат выполнения интерактивной программы


Ответы на контрольные вопросы:

1. 
   Что такое рекурсия и где её можно наблюдать в реальном мире?
   

Рекурсия - определение, описание, изображение какого-либо объекта или процесса внутри самого этого объекта или процесса, то есть ситуация, когда объект является частью самого себя. (Например x!- факториал в математике, матрешка, пирамида с кольцами, повторяющееся изображение в зеркалах)

2. 
   Что такое рекурсия в программировании?
   

Рекурсия в программировании – это когда вызов функции повторно вызывает ту же функцию до завершения первоначального вызова функции.

3. 
   Зачем применяются рекурсивные алгоритмы и когда их лучше всего использовать?
   

Рекурсия позволяет создавать код с неизменяемыми переменными, что:

• 
  делает код более читабельным,
  
• 
  защищает от ошибок типа «действия выполнены в не верном порядке», «использована не-инициализированная переменная» и других аналогичных,
  
• 
  облегчает организацию контроля корректности входных данных,
  
• 
  позволяет читать код с любого места, не просматривая его весь, отслеживая все изменения переменной,
  
• 
  облегчает отладку.
  

В некоторых случаях, рекурсия позволяет более ясно сформулировать идею алгоритма; например, это относится к алгоритму быстрой сортировки — quicksort — который рекурсивен по своей природе.

Но, конечно, использовать рекурсию следует разумно. Нужно учитывать то, что часто (не всегда) она ведёт к большим расходам стека и некоторому снижению производительности.

Кроме того, прибегая к рекурсии, надо понимать, какую выгоду вы можете от неё получить, и стремиться максимизировать выгоду и минимизировать вклад отрицательных качеств рекурсии.

Рекурсию будет лучше использовать при таких задачках: (например, обход вложенных каталогов), когда при этом у каждого имеется ряд своих отдельных переменных (например, количество файлов в данном каталоге), или асинхронных потоков, то поддерживать легче будет рекурсию. 
Рекурсивные алгоритмы имеют преимущество перед циклическими, когда значения переменных, участвующих в итерации, зависит от значения тех же переменной на предыдущей итерации.

Также рекурсию удобно использовать для обработки некоторых структур данных, например, деревьев.

4. 
   Какие бывают рекурсии в программировании?
   

• 
  Линейная рекурсия (рекурсивные вызовы на любом рекурсивном срезе, инициируют не более одного последующего рекурсивного вызова).
  
• 
  Повторительная рекурсия (частный случай линейной рекурсии с отсутствующими предварительными или отложенными вычислениями)
  
• 
  Каскадная (древовидная) рекурсия (нелинейная рекурсия).
  
• 
  Косвенная рекурсия (циклическая последовательность вызовов несколькими функциями друг друга).
  
• 
  Удаленная рекурсия (в теле функции при рекурсивных вызовах, в выражениях, являющихся фактическими параметрами, снова встречаются рекурсивные вызовы этой функции).
  

5. Что такое стек вызова функции?

Стек вызовов — LIFO-стек, хранящий информацию для возврата управления из подпрограмм (процедур, функций) в программу (или подпрограмму, при вложенных или рекурсивных вызовах) и/или для возврата в программу из обработчика прерывания.

6. На какие части делится рекурсивный алгоритм? Какие обязательные элементы должны присутствовать в нормальной рекурсивной функции?

Описание рекурсивной функции состоит из двух частей: базовой (base case) и рекурсивной (recursion case). Первая часть (base case) – это нерекурсивные ветви, где рассматриваются простейшие случаи, для которых ответ дается явно. В рекурсивном алгоритме минимум должна быть одна нерекурсивная ветвь, иначе при вычислении функции мы никогда не выйдем из рекурсии (формально цепочка рекурсивных вызовов окажется бесконечно длинной). Вторая часть (recursion case) – это рекурсивные ветви, где рассматривается общий случай решения задачи. Общий случай сводится к более простым аналогичным случаям, для решения которых рекурсивно применяется та же самая функция, а затем из полученных ответов строится окончательный ответ.

7. Что такое глубина рекурсии? Существует ли в языке Python ограничение на глубину рекурсии? Если да, то какова стандартная глубина рекурсии в языке Python?

Глубина рекурсии – максимальное количество активизированных и незавершённых вызовов одной и той же функции для фиксированного значения аргумента. Стандартная глубина рекурсии в языке Python – 999.

8. Какие именно ресурсы компьютера интенсивно использует рекурсивный алгоритм?

Рекурсивный алгоритм интенсивно использует оперативную память.

9. Что такое хвостовая рекурсия?

Хвостовая рекурсия — частный случай рекурсии, при котором любой рекурсивный вызов является последней операцией перед возвратом из функции.

10. Что можно сказать про алгоритмическую сложность (Big O) как по памяти, так и по операциям, выполняемых процессором, относительно двух подходов (один из которых базируется на циклах, а другой – на рекурсии) к решению итерационного характера задач?

В большинстве случаев циклический и рекурсивный подходы сопоставимы по алгоритмической сложности по числу операций, а по объему затрачиваемой памяти выигрывает циклический.

11. Что можно сказать относительно времени разработки алгоритма при использовании этих подходов?

Зачастую использование рекурсивного подхода сокращает время разработки алгоритма.

12. В каких областях или задачах не обойтись без рекурсивного подхода?

Без рекурсивного подхода не обойтись при вычислении чисел Фибоначчи, факториала, функции Аккермана, решении задачи о Ханойской башне и других.

ПРИЛОЖЕНИЕ А

Листинг исходных кодов программ

Файл 1

# Program calculates the sum of digits of a given number
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020


import model.sum_of_digits as sof


def main():
print('Calculation the sum of digits of a given number')
x=int(input('Input the integer number: '))
print('Cyclic computation:')
print('\nThe result is', sof.recurse_ds(x))
print('Recursive computation:')
print('\nThe result is', sof.cycle_ds(x))


if __name__ == '__main__':
main()
# sum_of_digits (model)
# Author: Rahman Daria

def cycle_ds(a):
#cyclic calculation the sum of digits
k=0
while a>0:
c=a%10
a//=10
k+=c
print(k, end=' ')
return k


def recurse_ds(a, k=0):
#recursive calculation the sum of digits
if a>0:
k = a%10 + recurse_ds(a//10, k)
print (k, end=' ')
return k


if __name__=="__main__":
a=74325
print (cycle_ds(a))
print (recurse_ds(a))
Файл 2

# Program determines whether the given number is a degree of
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.power_check as pc
import view.console_out as vi


def main():
print('Checking if the entered number a is a power of integer number n')
a = int(input('Input the number a: '))
n = int(input('Input the number n: '))
print('Cyclic computation:')
r=pc.cycle_power(a,n)
vi.output(r, a, n)
print('Recursive computation:')
r = pc.recurse_power(a, n)
vi.output(r, a, n)


if __name__=='__main__':
main()
# power_check (model)
# Author: Rahman Daria

def cycle_power(a, n):
k=1
while abs(a) > abs(n):
a/=n
k+=1
if a==n:
return k
else:
return -1


def recurse_power(a, n, k=0):
if a == 1:
return k
if abs(a) < abs(n):
return -1
return (recurse_power(a/n, n, k+1))


if __name__=="__main__":
a=74325
n=5
print (cycle_power(a,n))
print (recurse_power(a,n))
# console_out (view)
# Author: Rahman Daria

def output(r, a, n):
if r == -1:
print('The number', a, 'is not a power of the number', n)
else:
print('The number', a, 'is the number', n, 'to the', r, 'power')


if __name__=='__main__':
output(2, 25,5)
output(-1, 37, 3)
Файл 3

# Program raises a number to the indicated power
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.power as p
from datetime import datetime


def main():
print('Raising a float number x to an int power n')
x=float(input('Input the number x: '))
n=int(input('Input the power n: '))
print('Cyclic computation:')
print('The result is ', p.cycle_power(x, n))
print('Recursive computation:')
print('The result is ', p.recurse_power(x, n))
print('Recursive fast computation: ')
print('The result is ', p.recurse_fast_power(x, n, p=1))


if __name__=="__main__":
main()
# power.py (model)
# Author: Rahman Daria

def cycle_power(x, n):
#cyclic computataion
r=1
for _ in range(n):
r*=x
return r


def recurse_power(x, n, r=1):
#recursive computation
if n==0:
return r
n-=1
return x*recurse_power(x, n)


def recurse_fast_power(x, n, p=1):
#fast recursive computation
if n==0:
return p
if n%2==1:
p*=x
n-=1
return (recurse_fast_power(x**2, n/2, p))


if __name__=="__main__":
cycle_power(4, 3)

Файл 4

# Program find the max digit of the number
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.max_digit as m


def main():
print('Program determines the sum of digits of the integer number')
N=int(input('Input the number: '))
print('Cyclic computation:')
print('\nThe result is:', m.cycle_max_digit(N))
print('Recurse computation:')
print('\nThe result is:', m.recurse_max_digit(N))


if __name__=='__main__':
main()
# max_digit (model)
# Author: Rahman Daria

def cycle_max_digit(a):
max=0
while a>0:
c=a%10
a//=10
if c>max: max=c
print(max, end=' ')
return max


def recurse_max_digit(a, max=0):
if a>0:
c = a%10
if c> max: max=c
print (max, end=' ')
return recurse_max_digit(a//10, max)
return max


if __name__=="__main__":
a=74325
print (cycle_max_digit(a))
print (recurse_max_digit(a))

Файл 5

# Program calculates the Fibonacci numbers
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.fibonacci as fib

def main():
c=0
while(c!='4'):
print("""
==============Fibonacci series=============
Menu:
1. Output the Nth element
2. Output all the elements up to the Nth
3. Output the part of the series, the last
element of which does not exceed value X
4. Exit
""")
c=input()
if c == '1':
fib.Fibonacci(0)
elif c == '2':
fib.Fibonacci(1)
elif c == '3':
X = int(input('Input the value X: '))
if X<0:
print('There is no negative numbers in the Fibonacci series')
else:
print('Cycle computation: ')
f = 0; i = 1
while f<=X:
print(f, end=' ')
i+=1
f = fib.cycle_Fibonacci(i,0)
print('\n')
print('Recurse computation: ')
f = 0; i = 1
while f<=X:
print(f, end=' ')
i+=1
f = fib.recurse_Fibonacci(i)
elif c == '4':
print('Exit. Have a nice day!')
else:
print('Incorrect input. Try again')


if __name__ == '__main__':
main()

# fibonacci (model)
# Author: Rahman Daria

def cycle_Fibonacci(n, out):
# Calculating n-member of a Fibonacci sequence using cycle algorithm
fib1=0; fib2=1; i=1
while iif out: print(fib1, end=' ')
t = fib1
fib1 = fib2
fib2 += t
i += 1
return fib1

def recurse_Fibonacci(n):
# Calculating n-member of a Fibonacci sequence using recurse algorithm
if n==2:
return 1
if n<2:
return 0
return(recurse_Fibonacci(n-1)+recurse_Fibonacci(n-2))

def Fibonacci(out):
N = int(input('Input the index N: '))
if N <= 0:
print('Index must be positive')
else:
print('Cycle computation: ')
print(cycle_Fibonacci(N, out))
print('Recurse computation: ')
if out:
for i in range(1, N):
print(recurse_Fibonacci(i), end=' ')
print(recurse_Fibonacci(N))


if __name__=="__main__":
print(cycle_Fibonacci(6))
print(recurse_Fibonacci(6))

Файл 6

# Program calculates x^n/n!
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.function as f


def main():
print('Program calculates x^n/n!')
x=int(input('Input x: '))
n = int(input('Input n: '))
print('Cyclic computation\nThe result is: ', f.cycle_f(x, n))
print('Recurse computation\nThe result is: ', f.recurse_f(x, n))


if __name__=='__main__':
main()
# function (model)
# Author: Rahman Daria

def cycle_f(x, n):
F=1
for i in range(1, n+1):
F*=x/i
return F


def recurse_f(x, n):
if n<2:
return x
return x/n*recurse_f(x, n-1)


if __name__=='__main__':
print(cycle_f(3,3))
print(recurse_f(3,3))

Файл 7

# Program checks if the sum of digits of the number N matches the value of S
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.equals as eq


def main():
print('Checking if the sum of digits of the number N matches the value of S')
N=int(input('Input the number N: '))
S=int(input('Input the value S: '))
if eq.equals(N,S):
print('Yes, the sum of digits is ', S)
else:
print('No, the sum of digits is not ', S)


if __name__=='__main__':
main()

# equals.py (model)
# Author: Rahman Daria

def equals(N,S):
if recurse_ds(N)==S:
return True
return False


def recurse_ds(a, k=0):
#recursive calculation the sum of digits
if a>0:
k = a%10 + recurse_ds(a//10, k)
print (k, end=' ')
return k


if __name__=='__main__':
print(equals(123, 6))

Файл 8

# Program finds amount of dividers of the number
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.dividers as d


def main():
print('Calculating amount of dividers of the integer number')
N=int(input('Input the number: '))
print('\nThe number of dividers is', d.divs(N))

if __name__ == '__main__':
main()
# dividers (model)
# Author: Rahman Daria

def divs(x, a=2, k=0):
if x%a==0:
k+=1
print(a, end=' ')
if a==x-1:
return k
return divs(x,a+1,k)


if __name__=='__main__':
divs(36)
Файл 9

# Program calculates the sum of elements of the one-dimensional array
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.sum_of_elements as s
import util.array_build as b


def main():
print('Calculating the sum of elements of the one-dimensional sequence')
n=int(input('Input the number of elements in the sequence: '))
A=b.sequence_build(10, 100)
print('The sequence: ', A)
print('Cyclic computation:')
print('The result is: ', s.cycle_sum(A))
print('Recurse computation:')
print('The result is: ', s.recurse_sum(A))


if __name__=='__main__':
main()
# array_build (util)
# Author: Rahman Daria

def sequence_build(n, x):
#building array of n elements in range(-x, x)
from random import randint
ls=[0]*n
for i in range(n):
ls[i]=randint(-x,x)
return ls


if __name__=='__main__':
sequence_build(10,100)
# array_build (util)
# Author: Rahman Daria

def sequence_build(n, x):
#building array of n elements in range(-x, x)
from random import randint
ls=[0]*n
for i in range(n):
ls[i]=randint(-x,x)
return ls


if __name__=='__main__':
sequence_build(10,100)
Файл 10

# Program reverse the elements of the one-dimensional array
# main.py (controller)
# Author: Rahman Daria
# Group: 10702120
# Date: 16.03.2020

import model.reversing as r
import util.array_build as b


def main():
print('Reversing the elements of the one-dimensional sequence')
n=int(input('Input the number of elements in the sequence: '))
A=b.sequence_build(n, 100)
print('The original sequence:\n', A)
print('Cyclic algorithm:')
print('The reversed sequence:\n', r.cycle_reverse(A))
print('Recurse algorithm:')
print('The reversed sequence:\n', r.recurse_reverse(A))


if __name__=='__main__':
main()
# reversing (model)
# Author: Rahman Daria

def cycle_reverse(arr):
l=len(arr)
for i in range(l//2):
arr[i], arr[-(1+i)] = arr[-(i+1)], arr[i]
return arr


def recurse_reverse(arr):
if len(arr) != 1:
k=arr[-1]
arr=recurse_reverse(arr[:-1])
arr.insert(0,k)
return arr


if __name__=='__main__':
arr=[1,2,3,4,5,6,7,8,9,10]
print(cycle_reverse(arr))
print(recurse_reverse(arr))
# array_build (util)
# Author: Rahman Daria

from random import randint

def sequence_build(n, x, ls=[]):
#building array of n elements in range(-x, x)
if n==0: return ls
ls.append(randint(-x,x))
return sequence_build(n-1, x, ls)


if __name__=='__main__':
sequence_build(10,100)