Часть_1. Реновации паротурбинных установок

• Название: Реновации паротурбинных установок
• Дата: 09.11.2022
• Размер: 1.83 Mb.
• Имя файла: Часть_1.doc
• Тип: Документы; #778315
• страница: 4 из 8

Расчет и построение треугольников скоростей. Проведем этот расчет для осевой турбинной ступени, предполагая, что извест­ны давление , энтальпия и начальная скорость пара на входе в ступень, а также давления за сопловой р₁ и рабочей р₂ решетками. Следовательно, можно построить процесс в h,s-диа­грамме (см. рис. 3.2). Абсолютную скорость истечения пара из сопловой решетки можно определить из уравнения сохранения энергии:


(3.7)


г
(3.8)
де φ = c₁/c_1t— коэффициент скорости в сопловой решетке, за­висящий от режима течения пара и типа решетки, определяемый опытным путем; ρ — степень реактивности ступени; — распо­лагаемый теплоперепад ступени по параметрам полного торможения.. Тогда потери в сопловой решетке

,

где — коэффициент потерь энергии в сопловой решетке.

Отложив на h,s-диаграмме потерю энергии в сопловой решет­ке , построим действительный процесс АВ, где h₁ = h_1t + ΔH_с. Зная скорость c₁ и угол выхода пара из сопловой решетки α₁, построим вектор скорости

(рис. 3.5).

Струя пара входит в ра­бочую решетку с относительной скоростью 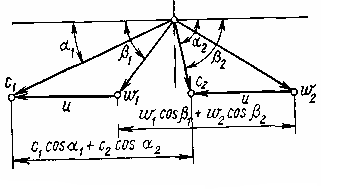, которая опреде­ляется разностью векторов и и составляет угол β₁ с направ­лением окружной скорости u. Скорость w₁ и угол β₁ ее на­правления можно определить графически или по формулам

(3.9)

. (3.10)

З
Рис 3.5 Треугольники скоростей пара в турбинной ступени
апишем уравнение сохранения энергии для относитель­ного движения без учета потерь в рабочей решетке (процесс DE — см. рис. 3.2):
(w²_2t-w²₁)/2=h_2t-h₁. (3.11)

Т
(3.12)
аким образом, при относительном движении в изоэнтропном процессе полная энергия пара на входе в рабочие лопатки рав­на полной энергии на выходе из них. Действительная скорость выхода пара меньше теоретической и составляет



где ψ = w₂/w_2t— коэффициент скорости в рабочей решетке.

Используя уравнение (3.11), определим относительную скорость выхода пара из рабочей решетки


(3.13)
.

П
(3.14)
отери энергии в рабочей решетке

,

где — коэффициент потерь энергии в рабочей решетке.

Направление относительной скорости w₂ определяется углом β₂, который зависит от формы и угла установки рабочих лопа­ток. Зная скорость w₂ и угол β₂, построим вектор скорости w₂ (см рис. 3.5).

Абсолютную скорость выхода пара из каналов рабочих лопа­ток с₂определяют как сумму векторов относительной w₂ и ок­ружной u скоростей. Скорость с₂ и угол α₂ ее направления мож­но найти графически или по формулам


(3.15)

(3.16)

Мощность и работа ступени. Мощность, развиваемая на ло­патках ступени, может быть определена как произведение ок­ружного усилия R_uна окружную скорость рабочих лопаток и:

. (3.17)

Полезная работа 1 кг пара, протекающего через рабочие ло­патки, т. е. удельная работа, определяется как отношение мощ­ности ступени к расходу пара через нее:

. (3.18)

Из треугольников скоростей следует

. (3.19)

Используя формулы (3.9) и (3.15), можно рассчитать удельную работу ступени
(3.20)
Из этого уравнения видно, что удельная работа в осевой сту­пени равна сумме двух величин: разности кинетических энергий на входе и выходе из рабочих лопаток в абсолютном движении и разности кинетических энергий на выходе и входе в относи­тельном движении.

Расчет удельной работы можно выполнить по балансу энер­гии на рабочих лопатках ступени. Теоретически 1 кг пара может совершить в ступени работу, равную располагаемой энергии Е_о. Под располагаемой энергией понимают сумму располагаемых теплоперепадов в сопловой и рабочей решетках


(3.21)

)


Действительная работа на рабочих лопатках меньше теоре­тической на значения потерь энергии в сопловой ΔH_с и рабочей ΔН_Р решетках, а также потерь, связанных с тем, что покидаю­щий ступень со скоростью с₂ поток пара отводит от нее кинети­ческую энергию

(3.22)

которую называют потерей с выходной скоростью. Таким об­разом, удельную работу ступени турбины можно определить по формуле

. (3.23)

Отрезок l, показанный на h,s-диаграмме (см. рис. 3.2), соот­ветствует работе, полученной на рабочих лопатках турбинной ступени.
3.3 Относительный лопаточный КПД ступени

Э
(3.24)
кономичность турбинной ступени характеризуется коэффици­ентом полезного действия. Относительным лопаточным КПД сту­пени называют отношение мощности, развиваемой на рабочих лопатках, к располагаемой мощности или отношение энергии (работы), полученной на рабочих лопатках, к располагаемой энергии:

.

Работу l обычно определяют по формуле (3.20) или (3.23), а располагаемую энергию Е_о— в зависимости от места ступени в многоступенчатой турбине. Если за ступенью находится камера, где поток тормозится, и энергия выходной скорости поэтому в последующих ступенях не используется, то Энергия с выходной скоростью промежуточной ступени может использо­ваться в последующей ступени полностью. В этом случае ее в располагаемую энергию данной ступени не включают, т. е. . В общем случае располагаемая энергия


(3.25)
,

где — коэффициент использования выходной скорости, изме­няющийся от 0 до 1.

Если кинетическая энергия с выходной скоростью полностью теряется, коэффициент 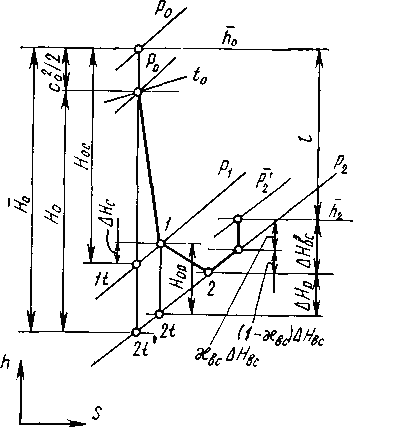= 0_, а если полностью используется, = 1.


Рис 3.6 h,s – диаграмма процесса расширения пара в турбинной ступени с частичной потерей энергии с выходной скоростью
На рис. 3.6 показана h,s-диаграмма процесса рас­ширения пара в турбинной ступени с частичной поте­рей энергии с выходной скоростью, равной

. (3.26)

Подставив в формулу (3.24) удельную работу lиз формулы (3.20), получим

относительный лопаточный КПД ступени


(3.27)
.

Относительный лопаточный КПД ступени η_о.л можно получить также из формулы

. (3.28)

Располагаемая энергия ступени


(3.29)
.

Е
(3.30)

сли вся энергия, которой располагает ступень, преобразует­ся в кинетическую энергию при коэффициенте использования выходной скорости _=0, то эквивалентную этой энергии скорость, называемую фиктивной, определяют по формуле

_.

Для любой ступени из треугольников скоростей (см. рис. 3.5) следует, что w₁cosβ_{1= c1cosα1 - u.} Для чисто активной ступени (ρ=0) при полной потере энергии с выходной скоростью ( =0) относительная теоретическая скорость на выходе из рабо­чей решетки равна относительной скорости на входе в нее w₁=w_2t. При этом располагаемая энергия ступени равна кинети­ческой энергии, подсчитанной по теоретической скорости на вы­ходе из сопловой решетки ^, а фиктивная ско­рость — теоретической скорости на выходе из сопловой решетки c_ф = c_1t. . Подставив значения w_2t, E_o и c_ф в формулу (3.27), полу­чим


(3.31)
.

Таким образом, η_о.л чисто активной ступени зависит от отношения скоростей u/c_ф, коэффициентов скорости в решетках φ и ψ, а также углов выхода из сопловой и рабочей решеток α₁ и β₂. Так как угол β₁ есть функция уг­ла α₁ и отношения скоростей u/c_ф, то он не является независи­мым параметром.

К
Рис 3.7 Зависимость относительного лопаточного кпд ступени от отношения скоростей u/c_ф
ак видно из формулы (3.31), наибольшее влияние на значение η_о.л оказывает отношение скоро­стей u/c_ф, которое зависит от час­тоты вращения ротора, а также диаметра и располагаемого теплоперепада ступени. Поэтому из отношение скоростей u/c_ф является одним важнейших параметров, определяющих экономичность ступени. При фиксированных зна­чениях φ,ψ,α₁ и _{cosβ2/cosβ1} за­висимость η_о.л от отношения ско­ростей u/c_ф изображается графи­чески параболой (рис.3.7), которая пересекает ось абсцисс при u/c_ф=0 и u/с_ф= cosα₁ , так как в этих точках η_о.л =0.

Максимальный КПД ступени η_о.л при ρ = 0 получают при оп­тимальном отношении скоростей

. (3.32)

Максимальный относительный лопаточный КПД чисто актив­ной ступени можно определить, подставив в формулу (3.31) формулу (3.32):

. (3.33)

Из формулы (3.33) следует, что максимальный КПД ступени η_о.л при ρ= 0 в большей степени зависит от коэффициента ско­рости в сопловой решетке φ и в меньшей степени — от коэффи­циента скорости в рабочей решетке ψ .

Зависимость КПД ступени η_о.л от отношения скоростей u/c_ф, приведенная на рис.3.7, отражает баланс энергии в чисто актив­ной ступени. Действительно, если формулу (3.28) переписать в от­носительных единицах, обозначив соответственно через ξ_с = ∆_Hс/E0, ξ_р = ∆_{Hр/E0 ,} ξ_в.с.= ∆_Hв.с./E0 относительные потери энергии в сопловой и рабочей решетках, и с выходной скоростью, получим

. (3.34)

Относительные потери энергии в сопловой решетке при по­стоянном коэффициенте скорости φ=const не зависят от отноше­ния скоростей u/c_ф.

Относительные потери энергии в рабочей решетке при по­стоянном коэффициенте скорости ψ=constзависят только от ха­рактера изменения отношений скоростей w₁/c_1t и u/c_ф. Из тре­угольников скоростей следует, что отношение w₁/c_1t увеличива­ется при уменьшении отношения u/c_ф. Таким образом, потери энергии в рабочей решетке ξ_p с увеличением отношения u/c_ф от нуля до значения, при котором угол входной скорости β₁ = 90°, уменьшаются. Дальнейшее увеличение отношения u/c_ф приводит к росту этих потерь энергии.

Рассматривая треугольники скоростей ступени для различ­ных отношений скоростей u/c_ф, можно заметить, что относитель­ные потери с выходной скоростью

(3.35)

достигают минимального значения при α₂=90°, так как в этом случае отношение скоростей с₂/с_1t минимально. При отклонении угла α₂ от 90° как в сторону увеличения, так и уменьшения по­тери с выходной скоростью растут.

Минимальные потери энергии с выходной скоростью получа­ют при отношении скоростей u/c_ф, близком к оптимальному.

Аналогично может быть получена зависимость относительно­го лопаточного КПД η_о.л от отношения скоростей u/c_ф и других факторов для одиночно расположенной ступени при любой сте­пени реактивности. Оптимальное отношение скоростей (u/c_ф)_опт для ступеней с любой степенью реактивности ρ приближенно определяют по формуле:

. (3.36)

Зависимость КПД ступени η_о.л и потерь энергии в ней при степени реактивности ρ = 0,5 показана на рис. 3.8.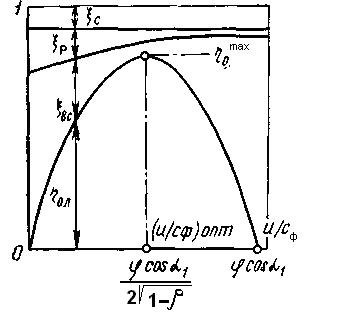

При сравнении ступеней, имеющих ρ=0 и ρ=0,5 видно, что оптимальное отношение скоростей u/c_ф во второй ступени в раза больше. При той же окружной скорости оптимальный теплоперепад ступени при степени реактивности ρ=0,5 в два раза меньше, чем ступени при степени реактивности ρ=0.

В
Рис 3.8 Влияние отношения скоростей u/c_ф на кпд реактивной ступени
се сказанное относительно оптимального отношения скоростей u/c_ф касалось случая, когдаx_в.с=0. Если определить КПД ступени η_о.л при x_в.с>0, оптимальное отношение u/c_ф будет выше, а его зависимость от отношения скоростей η_о.л=f(u/c_ф) – более пологой. Кроме того, необходимо учитывать, что в ступени есть и другие потери, которые будут рассмотрены в разделе 3.5.
3.4 Решетки турбин

Лопатки одной решетки устанавливают на равном расстоянии друг от друга. В одной решетке одинаковы размеры и тип про­филя лопаток, их шаг t,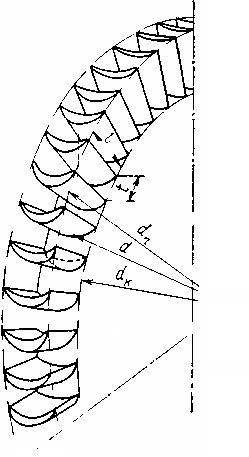

угол и диаметр установки. Сектор коль­цевой решетки показан на рис. 3.9.

Если геометрические харак­теристики лопаток изменяются по высоте l(т. е. размеры и фор­ма лопаток переменны по радиусу), их называют лопатками пе­ременного профиля (иногда — закрученными, или винтовыми). В случае, если профиль лопаток по ра­диусу не изменяется, их называют ци­линдрическими или лопатками постоян­ного сечения. Аналогично называют ре­шетки из таких лопаток. Если кольцевую решетку, показанную на рис.3.9, рассечь цилиндрической поверхностью и получен­ное сечение развернуть на плоскость, по­лучим так называемому плоскую решетку профилей, образующую сопловые (рис.

3
Рис 3.9 Сектор кольцевой решетки

.10, а) и рабочие (рис.3.10,б) каналы, обо­значения которых имеют на рис. 3.10, а, б соответственно индексы 1 и 2. Канал, об­разуемый соседними профилями, делит­ся на три участка: входной — от линии входных кромок до сечения О'; собственно канала — от сечения О' до расчетного выходного сечения О (в сужающихся ре­шетках сечение О называется горлом); косого среза — от выходного сечения О до линии выходных кромок. (см. рис. 3.10).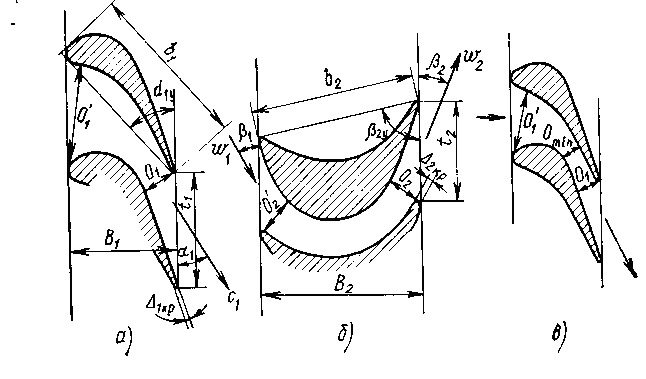



Рис 3.10 Сопловые (а,в) и рабочие (б) каналы турбинных решеток и их геометрические характеристики
Выпуклую часть профиля называют спинкой или стороной разряжения, а во­гнутую— стороной давления. Размеры профилей обозначают: хорду — b, шири­ну В, толщину выходной кромки — Δ_кр. Кольцевая решетка име­ет следующие геометрические характеристики: тип профиля ло­паток, угол их установки α_у или β_у, высоту l, средний диаметр d и шаг (где z — число лопаток). Для определения аэродинамических характеристик решеток прежде всего важны их относительные размеры: высота l=l/b, шаг t=t/b, длина 1/Θ = = l/d, толщина кромки а также эффективный (геометрический) угол .

Изменяя формулу профиля лопаток, шаг и угол их установ­ки, можно получить требуемую форму канала. Так, решетка, по­казанная на рис. 3.10, а, имеет суживающиеся каналы; их ширина на входе O'₁ значительно больше ширины O₁ на выходе. Решет­ка, показанная на рис. 3.10, б, имеет практически постоянное се­чение каналов. Решетка с каналами, которые сначала сужаются отO₁доO_min,, а затем расширяются от О_min до min О₁ показана на рис. 3.10, в. Такие решетки имеют каналы типа сопла Лаваля и иногда используются при сверхзвуковых скоростях.

Основными параметрами сопловых и рабочих решеток, уста­навливаемых в паровых турбинах, являются:

скорость пара на выходе из решетки (число Маха М) М_1t=с_1t/а₁ и M_2t= w_2t/a₂ (где а₁ и а₂ — скорости звука, определяемые соответственно по параметрам пара на выходе из соответст­вующей решетки);

число Рейнольдса (число Re), характеризующее влияние сил вязкости, и (где b₁ и b₂—хорды; v₁ и v₂ — кинематические вязкости);

угол входа пара в решетку α_о или β₁;

влажность пара у=1—х (где х— степень сухости пара в со­ответствующих сечениях решеток).

Иногда кроме этих параметров используют также начальную степень турбулентности, неравномерность полей параметров, раз­меры капель влажного пара и др.

Применяемые в паровых турбинах решетки можно в зависи­мости от назначения, числа М, относительной высоты, веерности и других признаков разделить на несколько групп. Так, по на­значению решетки турбин подразделяют на сопловые (рис.3.11,а-г) и рабочие (рис.3.11,д-з). В пределах каждого из этих типов решеток их можно разделить на несколько групп по числу Маха.

На заводах при изготовлении паровых турбин подбирают со­ответствующие аэродинамические отработанные профили, исполь­зуя отраслевые нормали.

В зависимости от числа Маха принята следующая классифи­кация сопловых и рабочих решеток:

типа А (дозвуковые) при М<0,7 0,9;

типа Б (околозвуковые) при 0,9<М<1,15;

типа В (сверхзвуковые) при 1,1<М<1,3;

типа Р (расширяющиеся —сопла Лаваля) при М>1,3-1,5.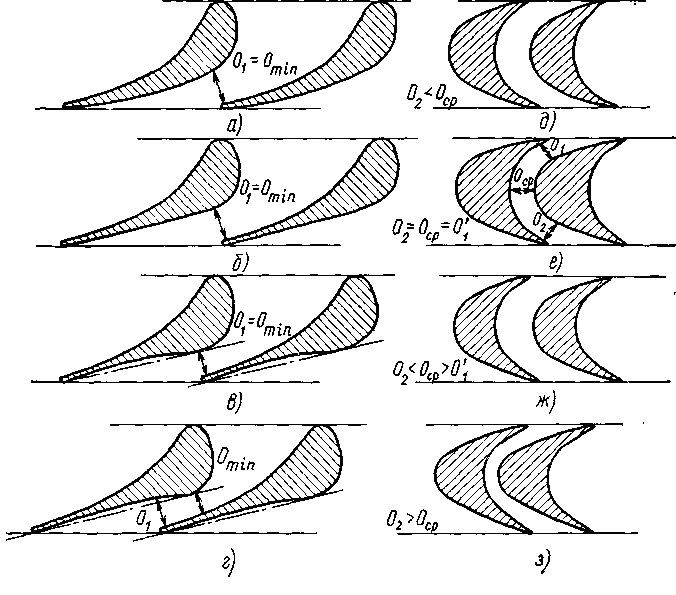


Рис 3.11 Реактивные сопловые (а,б,в,г) и рабочие (д,е,ж,з) решетки
Профили типа А (рис.3.11,а, д) имеют обводы с плавно меня­ющейся кривизной и образуют межлопаточные каналы, плавно суживающиеся к выходу. Профили типа Б (рис.3.11,б, е) имеют прямолинейные участки на спинке в косом срезе и образуют су­живающиеся каналы. Профили типа В (рис.3.11,в) имеют вогну­тую поверхность спинки в косом срезе и образуют суживающие­ся каналы. Профили типа Р (рис.3.11,г, д) образуют каналы ти­па сопла Лаваля.

Принята следующая система обозначения решеток. Первая буква С или Р указывает назначение решетки (сопловая или ра­бочая), следующие за ней через дефис две первые цифры — рас­четный угол входа в градусах, две вторые — угол выхода, а бук­ва после них — тип решетки по числу Маха. Например, обозна­чение С-90-15Б расшифровывается так: сопловая решетка с рас­четным углом входа 90°, угол α_1э== 15°, околозвуковая на число 0,9<М<1,15.

Для расчета и проектирования турбинных ступеней необхо­димо знать энергетические и аэродинамические характеристики сопловых и рабочих решеток, важнейшими из которых явля­ются:

коэффициенты потерь энергии _и (или соответственно коэффициенты скорости _{и ),}

коэффициенты расхода и ,

углы выхода потока α₁ и β_2.

Энергетические и аэродинамические характеристики решеток зависят как от их геометрии, так и от режимных параметров. Существующие теоретические методы определения коэффициен­тов ξ, µ и угла выхода, особенно с учетом вязкости, сжимаемо­сти, влажности, нестационарности и неравномерности потока, весьма громоздки, трудоемки и недостаточно точны. Поэтому в настоящее время аэродинамические характеристики определя­ют чаще всего опытным путем или на основании обобщения экс­периментальных исследований.

Потери в решетках могут быть нескольких видов. Значитель­ную долю составляют профильные потери, которые определяют­ся в первую очередь трением пара в его пограничном слое и вихрями за выходной кромкой лопатки. Большие потери возни­кают также в концевых областях лопаток (концевые потери) вследствие трения пара на стенках, ограничивающих канал по высоте, и вихреобразования у концов лопаток. Кроме профиль­ных и концевых возникают другие потери, например от взаимо­действия решеток, влажности пара и т. д. Для оценочных расче­тов турбинных ступеней в большинстве случаев принимают ко­эффициенты скорости φ = 0,95-0,97 и ψ = 0,91-0,93, а также коэффициенты расхода µ=0,93-0,98 при работе на перегретом паре и µ=0,94- 1,04 — на влажном.
3.5 Относительный внутренний КПД ступени

Рассмотренный ранее относительный лопаточный КПД ступени η_о.л характеризует качество ее решеток и потери энергии с вы­ходной скоростью. В ступени есть и другие потери, которые на­зывают дополнительными. К ним относят:

потери трения диска и лопаточного бандажа ξ_тр;

потери, связанные с парциальным подводом пара в ступени ξ_п;

потери от протечек пара в зазорах между статором и рото­ром ξ_у;

потери от влажности ξ_вл.

Учитывающий все эти потери КПД называют относительным внутренним КПД ступени