Часть_1. Реновации паротурбинных установок

• Название: Реновации паротурбинных установок
• Дата: 09.11.2022
• Размер: 1.83 Mb.
• Имя файла: Часть_1.doc
• Тип: Документы; #778315
• страница: 3 из 8

Уравнение неразрывности. Это уравнение выражает закон сохранения массы для движу­щейся среды. Выделим в сопле два сечения 1—1 и 2—2 с площадями F₁ и F₂, перпендикулярными направлению движения потока. Массовым расходом D газа на­зывают массу вещества m, кото­рая протекает через поперечное сечение сопла в единицу време­ни τ, т. е. D = m/τ. При устано­вившемся течении массовый расход D через любое сечение ка­нала будет неизменным:

. (2.5)

Объемный расход газа через первое сечение сопла

_, (2.6)

где c₁ — скорость потока газа.

Объемный расход газа определяется как

V₁ =D₁*v₁ ,(2.7)

где v₁ — его удельный объем.

П
(2.8)
риравнивая уравнения (28) и (27), получим

или .

Д
(2.9)
ля второго сечения соотношения будут аналогичны:

D₂v₂=F₂c₂или D₂=(F₂c₂)v₂.

Т
(2.10)
ак как D₁=D₂=D, получим

D=(F₁c₁)v₁=(F₂c₂)/v₂=(cF)/v= ρcF=const,

где ρ =1/ v – плотность газа.

Т
(2.11)

огда для любого сечения

Dv=Fc.

Уравнение сохранения энергии. Запишем первый основной закон термодинамики (закон сохранения и превращения энергии) для потока 1 кг газа, протекающего от сечения 1—1 до сечения 2—2 сопла:

, (2.12)

где q — теплота, подведенная к потоку; — разность энтальпий, — разность кинетических энергий и _g(z2-z1) —разность потенциальных энергий в сечениях 1—1 и 2—2; l — работа, совершаемая газом на этом участке.

Если пренебречь изменением потенциальной энергии g(z₂-z₁), так как она мала, то уравнение (2.12) примет вид

q=h₂-h₁+(c₂²-c₁²)/2+l(2.13)

или

h₁+c₁²/2+q=h₂+c₂²/2+l. (2.14)

Соотношение (2.14), являющееся уравнением сохранения энер­гии для установившегося движения газа, справедливо независи­мо от того, сопровождается ли течение газа в системе потерями или происходит без потерь.

Если газ протекает через сопло при отсутствии теплообмена с внешней средой (q=0) и подвода или отвода механической энергии (l= 0), уравнение (2.14) принимает вид

(c₂²-c₁²)/2=h₁-h₂. (2.15)

Таким образом, при отсутствии обмена теплотой и механиче­ской энергией с внешней средой изменение кинетической энергии определяется разностью энтальпий, или теплоперепадом, между рассматриваемыми сечениями.

Уравнение количества движения. Будем исходить из основно­го закона динамики: ускорение прямо пропорционально силе и обратно пропорционально массе: a=F/m (второй закон Нью­тона). Количеством движения (или импульсом) называется ве­личина, равная произведению массы тела на скорость: Fτ=p=mc. Как и скорость импульс — величина векторная, используя понятие импульса, можно сформулировать основной закон динамики так: сила равна изменению импульса в единицу вре­мени, т. е.

(2.16)

Для замкнутых систем тел справедлив закон сохранения им­пульса, который можно сформулировать так: суммарный им­пульс замкнутой системы сохраняется при любых процессах, происходящих в ней.

Второй и третий законы Ньютона позволяют решить по су­ществу любую задачу механики. Правда, в некоторых случаях применение этих законов может быть связано с большими трудностями.

При установившемся движении импульс некоторой массы га­за в данном сечении остается постоянным. При переходе в дру­гое сечение импульс изменяется вследствие действия сил давле­ния и вязкости, внешних сил и др. При отсутствии обмена теп­лотой и механической энергией с внешней средой, а также вяз­кости, получим уравнение импульса, учитывающее только силы давления:

(2.17)

где R₁=p₁F₁ и R₂=p₂F₂ cилы давления в сечениях 1-1 и 2-2; m/τ=D – секундный расход газа.

Используя выражение D=Fc/v= ρcF, получим

(2.18)

(2.19)

или



Формулу (2.17) называют уравнением импульсов для потока идеального сжимаемого газа (без учета внешних воздействий и сил тяжести).

Если кроме сил давления необходимо также учитывать дру­гие силы, то в уравнении (2.17) под разностью сил R₁—R₂ пони­мают равнодействующую всех сил в проекции на направление движения.

Термическое уравнение состояния. Это уравнение связывает основные параметры состояния газа: давление р, температуру Т и удельный объем v. Для идеального газа

pv=RT или p =ρRT, (2.20)

где R— универсальная газовая постоянная.

Уравнение (2.20) легко получают из законов Бойля — Мариотта и Гей-Люссака.

Калорическое уравнение состояния. Под калорическими свой­ствами понимают внутреннюю энергию u, энтальпию h, изобар­ную C_p и изохорную C_v теплоемкости. Согласно уравнению Мен­делеева — Клапейрона, энтальпия

. (2.21)

По уравнению Майера

С_p = С_v + R(2.22)

можно определить универсальную газовую постоянную

. (2.23)

Отношение называют показателем адиабаты k. Показатель адиабаты перегретого водяного пара изменяется в преде­лах от 1,26 до 1,33, а для сухого насыщенного пара составляет 1,135.

Иногда калорическое уравнение состояния для реального га­за записывают в виде зависимости энтальпии от давления и тем­пературы. Для адиабатного процесса калорическое уравнение состояния имеет вид

(2.24)

(2.25)


или


.
Т 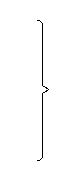аким образом, решив систему уравнений (2.10), (2.15), (2.19), (2.21) и (2.25), которая является математической формулировкой общих законов течения газа,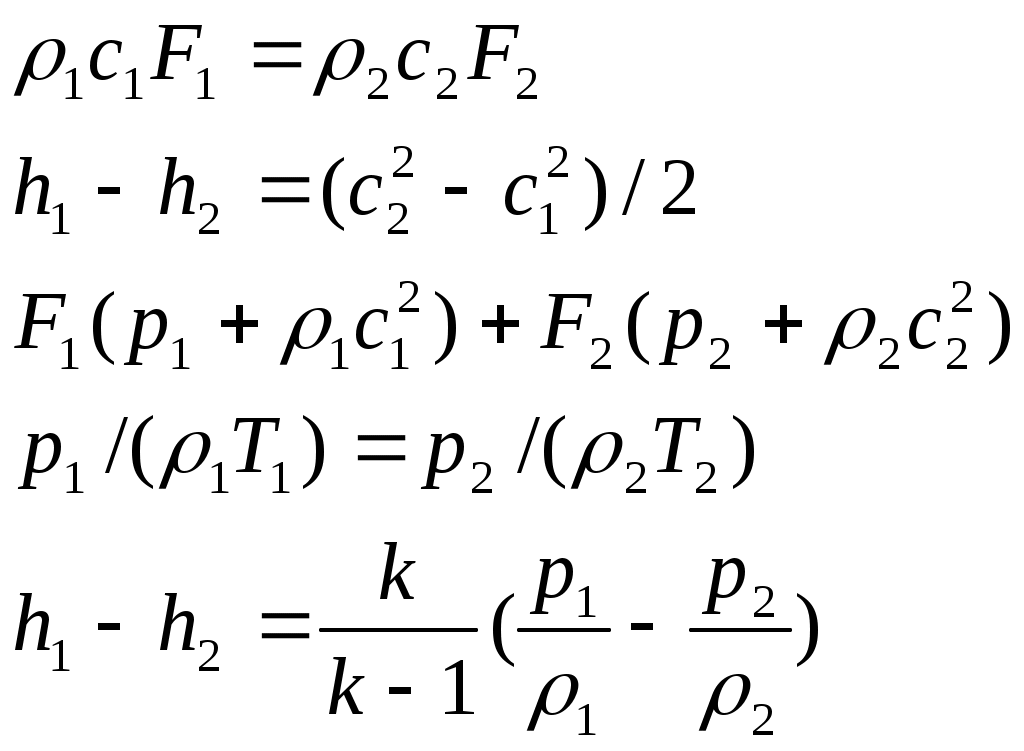

(2.26)



можно найти его параметры в любом сечении сопла. Так, если известны параметры газа в сечении 1—1, показатель адиабаты k и площади F₁ и F_2, можно, решив систему уравнений (2.26), оп­ределить пять неизвестных параметров в сече­нии 2—2.
2.2 Течение пара через сопла и каналы. Влияние сил трения

Рассмотрим, как должна изменяться площадь Fпроходного се­чения сопла или любого другого канала по мере расширения ра­бочего тела при различных режимах (дозвуковых и сверхзвуко­вых) течения. В качестве рабочего тела здесь и в дальнейшем будем рассматривать водяной пар.

Из уравнения неразрывности (2.10) можно получить формулу, связывающую изменение скорости потока с изменением сечения канала:

, (2.27)

где ∆с, ∆_{F -} приращение скорости пара и площади канала.

Из этой формулы вытекает важное следствие: скорость до­звукового потока возрастает при сужении канала и уменьшает­ся при его расширении и, наоборот, сверхзвуковой поток ускоряется при расширении канала и замедляется при его сужении.

Таблица 2.1 Изменение скорости потока в каналах

Поток	Канал
	Суживающийся ΔF<0	Расширяющийся ΔF>0
Дозвуковой M<1	Поток ускоряется ΔC>0	Поток замедляетсяΔC<0
Сверхзвуковой M>1	Поток замедляетсяΔC<0	Поток ускоряется ΔC>0

Из формулы (2.27) следует, что для получения сверх­звуковой скорости на выходе из сопла, если на его входе ско­рость близка к нулю (или дозвуковая), необходимо специально профилировать сопло: оно должно сужаться на начальном участ­ке, а затем расширяться. При достаточно большой разности дав­лений скорость потока в самом узком сечении сопла станет рав­ной местной скорости звука, а дальнейшее ускорение сверхзву­кового потока будет происходить на расширяющемся участке (табл.2.1). Работающее так сопло называют соплом Лаваля и применяют в паровых и газовых турбинах, реактивных двигателях.

Распределение параметров пара (давления р, скорости с, удельного объема v), а также изменение площади вдоль сопла Лаваля показано на рис. 2.6,а. Эскиз этого сопла показан на рис. 2.2,б.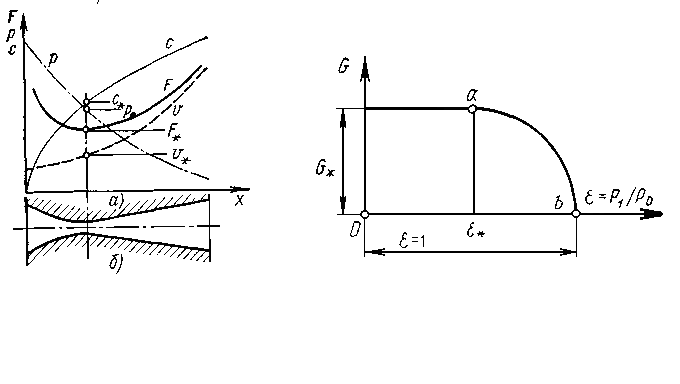



Рис 2.2. Распределение параметров Рис 2.3. Зависимость расхода пара пара вдоль сопла Лаваля (а) и его через сопло от отношения давлений эскиз (б) ε
Самое узкое сечение сопла называют критическим и обо­значают его площадь F_*. Соответственно скорость, давление и удельный объем в этом сечении также называют критическими и обозначают с_*, р_*иv_*. Скорость пара от входа сопла до кри­тического сечения меньше скорости звука, а в критическом сече­нии она равна скорости звука. В сечениях после критического и до выхода из сопла течение пара происходит со сверхзвуковой скоростью.

Расход пара можно определить из уравнения неразрывности (2.10):

, (2.28)

где отношение давления за соплом к давлению торможения перед соплом.

Формула (2.28) позволяет определить зависимость расхода па­ра D через сужающееся сопло, имеющее площадь F выходного сечения, от отношения давлений ε — кривая ab на рис.2.7. Эта формула справедлива при дозвуковом течении пара, т. е. отно­шении давлений больше критического (ε> ε _*), и не учитывает потери энергии. При сверхзвуковом течении пара, т. е. отношении давлений меньше критического (ε<ε_*), расход остается по­стоянным и равным критическому D_*.

С учетом потерь энергии действительный расход пара D_д бу­дет меньше подсчитанного по формуле (2.28):

D_д =μD, (2.29)

где μ — коэффициент расхода, всегда меньший единицы и зави­сящий от отношения давлений и параметров пара.
2.3 Определение размеров сопл

при дозвуковых и сверхзвуковых скоростях

Процесс изменения параметров пара при расширении без учета потерь энергии происходит по адиабатному закону pv^k=const и изображается линией AD на h,s-диаграмме (рис. 2.4).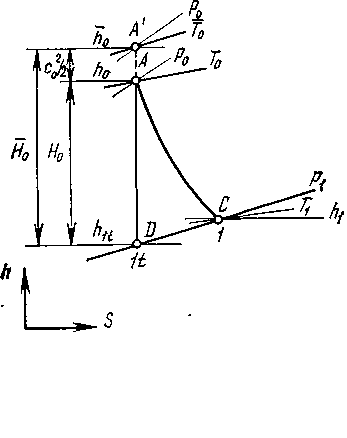


Рис. 2.4 h, s-диаграмма процессов из­менения параметров пара при его расширении без учета потерь энергии и с учетом их
В дейст­вительном процессе необходимо учитывать потери энергии. В этом случае процесс расширения пара приближенно подчиня­ется уравнению политропы

. (2.30)

Показатель политропы n для каждого конкретного случая течения должен иметь вполне определенное значение, зависящее от сил трения, но он всегда больше показателя изоэнтропы k, т. е.n>k . Этот формальный прием значительно облегчает мате­матическое исследование различных случаев течения пара с учетом вязкости. Однако следует иметь в виду, что применение eго имеет ограничения, так как действительный процесс при течении с трением не является строго политропным.

Таким образом, из-за действия сил трения при течении пара часть механической энергии превращается в теплоту трения. В результате энтропия газа при его теплоизолированном течении возрастает и в этом случае процесс в h,s-диаграмме изображает­ся кривой АС. Как видно из рис. 2.4 при одинаковом перепаде давлений (р₀—p₁) энталь­пия в конечном состоянии при течении с трением (точ­ка С) будет больше энталь­пии в конечном состоянии при течении без трения (точка D).

Из уравнения сохранения энергии (2.15) следует, что располагаемый теплоперепад

(2.31)

больше действительного теплоперепада

(2.32)

на значение потерь энергии

_. (2.33)

Отношение скорости пара c₁ в действительном процессе АС к теоретической скорости пара c_1t в идеальном (т. е. протекающем без трения) процессе AD, происходящих при одинаковом перепаде давлений, называют коэффициентом скорости

. (2.34)

Из уравнения сохранения энергии

где — так называемый располагаемый теплоперепад по параметрам торможения.

Таким образом, для определения скорости те­чения пара при наличии трения нужно вычислить скорость иде­ального течения и умножить полученное значение на коэффициент скорости φ. Коэффициенты скорости в разных соплах раз­личны, и их значения определяют опытным путем. Для сопл сов­ременных турбин они изменяются от 0,95 до 0,98.

При течении пара часть его кинетической энергии вследствие действия сил трения необратимо превращается в теплоту, вы­деляющуюся в поток. Эта теплота компенсирует уменьшение внутренней энергии пара, т. е. повышает его температуру и ра­боту расширения. Часть теплоты трения, затрачиваемая на ра­боту расширения пара, преобразуется в энергию его движения, а остальная часть является потерей полезной работы.

Потерю кинетической энергии или располагаемого теплопере­пада при течении с трением определяют по уравнению: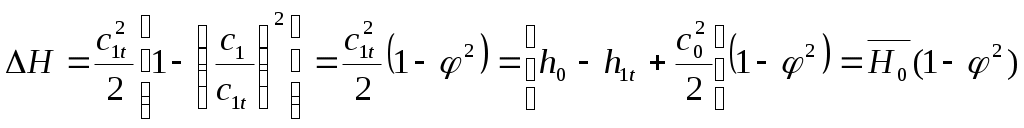

. (2.35)

Величину, характеризующую потерю работы из-за действия сил трения, называют коэффициентом потери энергии

(2.36)

откуда потеря располагаемого теплоперепада

_{∆H = ς .}(2.37)

При обтекании паром стенки канала, в частности турбинной лопатки, влияние вязкости, а следовательно, и сил трения обыч­но ограничивается небольшой зоной непосредственно возле стен­ки. Вдали от стенки силы трения можно не учитывать. Очевид­но, и это подтверждается опытами, что скорость потока в этой зоне должна изменяться от нуля на стенке, где поток как бы «прилипает» к ней и полностью заторможен, до скорости в так называемом ядре потока, где влияние сил трения практически не сказывается.

Тонкий, прилегающий к стенке слой потока, в котором ско­рость изменяется от нуля, что соответствует условию прилипа­ния, до значения, соответствующего движению без трения, на­зывают пограничным слоем. Пограничный слой тем тоньше, чем меньше вязкость. Так как внутри пограничного слоя в направле­нии, перпендикулярном движению, скорость изменяется доволь­но быстро, то даже при очень малой вязкости здесь возникают такие силы трения, которые сравнимы с силами инерции и поэ­тому не могут быть отброшены. В то же время вдали от стенок силы трения по сравнению с силами инерции ничтожно малы.

В зависимости от режима течения различают ламинарный и турбулентный пограничные слои. При ламинарном течении слои пара перемещаются параллельно, не перемешиваясь. Турбулент­ное течение сопровождается сильным перемешиванием движущегося пара, в котором наблюдаются пульсации скорости. При­меры распределения скоростей в ламинарном (кривая 1) и тур­булентном (кривая 2) пограничных слоях показаны на рис. 2.5.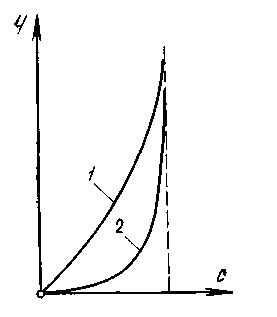



Рис. 2.5 Распределение скоростей в ламинарном и турбулентном пограничных слоях
Основным критерием, определяющим влияние вязкости, в част­ности режим (турбулентный или ламинарный) пограничного слоя и его толщину, является безразмер­ное число Рейнольдса, или число Re:

Re = cx/ν,(2.38)

где с — скорость потока, х — характер­ный размер обтекаемого тела (например, хорды лопатки), ν — кинематическая вяз­кость пара.

При решении практических задач для большей части потока вне пограничного слоя используют уравнения движения без учета сил трения (уравнения идеального газа). Зону пограничного слоя рассчиты­вают по полуэмпирическим уравнениям, учитывающим влияние сил трения, кото­рые зависят от числа Re.

Определение размеров сопловых и ра­бочих решеток турбин в основном бази­руется на двух уравнениях: неразрывно­сти и сохранения энергии. Как правило, скорости определяют по уравнениям идеального газа, а силы трения учитывают введе­нием в уравнение неразрывности коэффициента расхода μ.

Сопловые (и рабочие) каналы в турбинах образуются опре­деленным образом установленными лопатками, которые составляют кольцевую сопловую решетку. В турбинах применяют соп­ловые решетки как с полным подводом (рис. 2.6,а), в которых ло­патки расположены по всей окружности, так и с парциальным (рис. 2.6,б), в которых лопатки размещаются только на части окружности. Две соседние лопатки высотой l показаны на рис.2.6, в.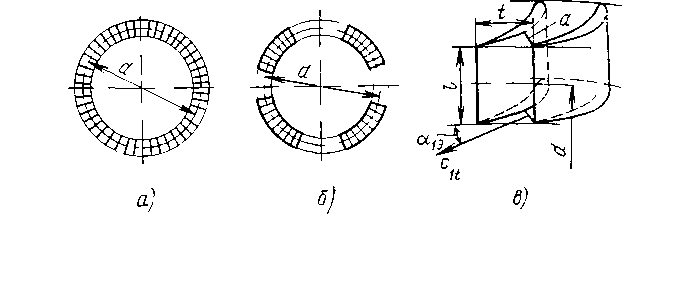



Рис 2.6 Расположение каналов по окружности сопловых решеток с полным (а) и парциальным (б) подводами пара, две соседние лопатки (в), устанав­ливаемые в этих решетках.
Расстояние, на котором располагаются по отношению друг к другу лопатки, образующие канал, называют шагом t решетки (рис. 2.10, в). Если средний диаметр решетки обозначить d, то степень парциальности

, (2.39)

где z— число лопаток (каналов).

Таким образом, как следует из формулы (2.41), степень пар­циальности — это отношение длины дуги, занятой сопловыми ло­патками, к длине окружности, на которой они расположены. Очевидно, что при полном подводе пара степень парциальности е = 1 и произведение шага решетки на число каналов равно дли­не окружности: zt=πd.

Для определения размеров решеток необходимо правильно выбрать соответствующие профили лопаток и рассчитать высоту их выходного сечения. Решетки с дозвуковым течением пара (рис. 2.6, в) имеют площадь выходного сечения, равную произ­ведению ширины минимального сечения а, называемой горлом канала, на высоту l. В таких решетках

^, (2.40)

где α_1э — эффективный (геометрический) угол выхода потока из решетки.

Площадь сопловой решетки определяют по уравнению нераз­рывности

. (2.41)

Удельный объем v_1tи скорость с_1t пара можно определить по изоэнтропному процессу (см. точку D на рис. 2.4). В частности, удельный объем v_1t — по h,s-диаграмме или по уравнению изоэнтропы, а скорость c_1t — по формуле (2.31). Зная площадь на выходе из сопловой решетки

, (2.42)

можно определить высоту лопаток

_. (2.43)

Как уже отмечалось, при дозвуковом течении (ε> ε _*) расширение пара происходит в сужающейся части сопла. При этом давление р₁ в минимальном сечении О - А сопла (рис. 2.7) равно давлению за ним.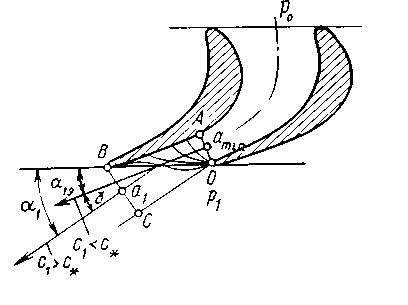



Рис. 2.7 Расширение пара в косом срезе сопла
Критическую скорость за соплом с_кр = а получают в сечении О - А при отношении давлений, равно­му критическому ε = ε_* . В дозвуковом потоке (ε >=ε_*) косой срез сопла ОАВО служит только для направления потока пара под углом α_1э .

В сверхзвуковом потоке (ε ‹ ε _*) расширение пара до критического давления p_кр также происходит в суживающейся части сопла. При этом в сечении О—А сопла устанавливается критическая скорость пара, а его дальнейшее расширение от р_кр до р₁ происходит в косом срезе ОАВО. В этом случае поток перестает быть симметричным относительно оси сопла.

Для выяснения явлений, происходящих в косом срезе, рас­смотрим отдельные струйки потока. Часть потока у кромки в точке О попадает из области с давлением р_кр в сечении ОА в камеру за соплом с давлением p₁<р_кр. Расширение пара проис­ходит в камере за соплом от давления р_кр до р₁. Часть потока у поверхно­сти лопатки АВ расширя­ется от давления р_кр до давления в точке В так же, как в сопле Лаваля, т. е. по мере движения потока давление посте­пенно снижается от p_кр до р₁. При этом тепловая энергия потока преобра­зуется в кинетическую (поток ускоряется).

Соединив точки с оди­наковыми давлениями, по­лучим пучок изогнутых изобар, которые собираются в точке О, где давление резко изме­няется от р_кр до р₁.

В сверхзвуковом потоке, как отмечалось, пло­щадь сечения струи в соответствии с уравнением неразрывности должна увеличиваться. Поскольку в косом срезе сопла поток па­ра ограничен только с одной стороны поверхностью АВ, увели­чение его площади возможно лишь при увеличении угла поворо­та от α_1э до α_1Э+δ. Угол отклонения потока δ можно рассчитать следующим образом.

Расходы пара в сечениях О—А и В—С одинаковы и состав­ляют

, (2.44)

где F_min и F₁ — площади в сечениях О - А и В - С.

При одинаковой высоте решетки в сечениях О - А и В - С их площади прямо пропорциональны ширине сопла:

. (2.45)

Из треугольников ОАВ и ОВС определим

и . (2.46)

П
(2.47)
о формулам (2.46), (2.47) и (2.48) можно определить угол вы­хода потока из сопла

.

Зная угол выхода сверхзвукового потока из сопловой решет­ки, можно по формуле (2.43) определить ее высоту l₁ .

3. СТУПЕНЬ ТУРБИНЫ

3.1 Преобразование энергии в ступени турбины

Преобразование энергии рассмотрим на примере осевой турбин­ной ступени (рис. 3.1, а).

Турбинные ступени, в которых поток пара движется по поверхностям, близким к цилиндрическим, на­зывают осевыми.

Сопловые лопатки 2 образуют кольцевую сопловую решетку, укрепленную в диафрагме 1, которая закреплена в неподвижном корпусе 3. Рабочие лопатки 4, закрепленные на диске 5, образу­ют рабочую решетку. Диск с рабочими лопатками, называемый рабочим колесом, закреплен на валу 6 и вращается вместе с ним. Вал и рабочее колесо являются ротором турбины.

Совокупность неподвижной сопловой решетки со своей вра­щающейся рабочей решеткой называют ступенью турбины.

В каналах, образованных сопловыми лопатками 2, давление пара изменяется от давления перед ступенью p₀ до давления р₁ за ней (рис. 3.1,б). В каналах сопловой решетки, как указыва­лось ранее, происходит преобразование тепловой энергии пара в кинетическую. Вследствие падения давления скорость пара на выходе из сопловой решетки повышается до c₁. Направление этой скорости (угол α₁) определяется профилем сопловых лопа­ток и углом их установки.

С 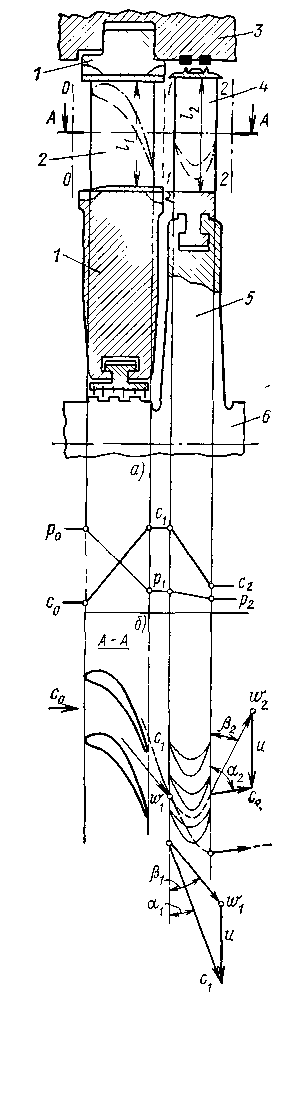корость c₁ одновременно является абсолютной скоростью входа пара на лопатки 4 рабочего колеса. Относительная же скорость входа w определяется из параллелограмма скоростей , где u₁ — переносная, или окружная, скорость рабо­чих лопаток в сечении 1—1 (рис. 3.1,а). Обычно вместо паралле­лограмма скоростей строят треугольник скоростей (сечение А-А).

В рабочей решетке кинетиче­ская энергия пара преобразуется в механическую энергию вращения вала. Пар покидает рабочую ре­шетку с абсолютной скоростью с₂, которая является векторной суммой относительной w₂ и окружной u₂ скоростей. При этом относительная скорость в общем случае может по­вышаться от w₁ на входе в рабочую решетку до w₂ на выходе из нее вследствие дальнейшего падения давления от p₁ до р₂. Угол β₂ на­правления относительной скорости на выходе также определяется про­филем рабочих лопаток и углом их установки. Полученный треугольник называют выходным треугольником скоростей.

Процессы расширения в турбин­ной ступени в h,s-диаграмме при изотропном (A1_tC) и реальном (A12) его течениях показаны на рис. 3.2.

С
Рис. 3.1 Осевая турбинная сту­пень (а) и распределение пара­метров пара в ней (б); 1 — диафрагма, 2,4 — сопловые и рабочие лопатки, 3,6 — корпус и вал турбины, 5 — диск ступени

огласно уравнению энергии разность энтальпий на входе и вы­ходе из ступени турбины по затор­моженным параметрам со­ответствует теплоте, преобразован­ной в механическую энергию l на рабочих лопатках. В результате потерь в сопловой решетке распола­гаемый теплоперепад в рабочей ре­шетке H_op = h_D—h_E = h₁—h_2t в ре­альном процессе DE больше ее рас­полагаемого теплоперепада H'_ор = = h_В - h_c при теоретическом процес­се ВС в сопловой решетке (h_oр>h'_оp) вследствие возврата тепло­ты. При этом потери энергии в пре­дыдущей сопловой решетке повы­шают температуру пара на входе в следующую рабочую решетку (t_D>t_B). Однако разница между H_oр и H'_ор обычно настолько мала, что с достаточной точностью можно принять H_{о р} ≈ H'_ор.

Отношение располагаемого теплоперепада в рабочей решетке к располагаемому теплоперепаду всей ступени (от параметров торможения) называют степенью реактивности ступени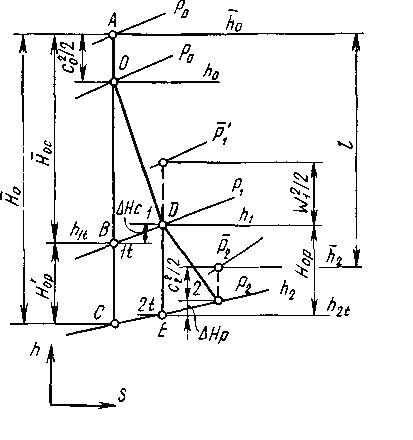

. (3.1)

П ри степени реактивности, равной нулю, в каналах рабочей решетки не происходит дополнительного расширения пара. Та­кую ступень называют чисто активной. Если степень реактивно­сти не превышает 0,20—0,25, ступень называют активной, а иногда — активной с не­большой степенью реактив­ности в отличие от чисто ак­тивной. При значительной степени реактивности (0,4 — 0,6 и более) ступень назы­вают реактивной.

На рис. 3.3,а-в показа­ны треугольники скоростей, сопловые 1 и рабочие 2 ло­патки турбинных ступеней со степенями реактивности ρ, равными 0; 0,2; 0,5 и 0,7, и h,s-диаграммы процессов в этих ступенях.


Рис. 3.2 h,s – диаграмма процесса

расширения пара в турбинной ступени

без учета потерь энергии с выходной скоростью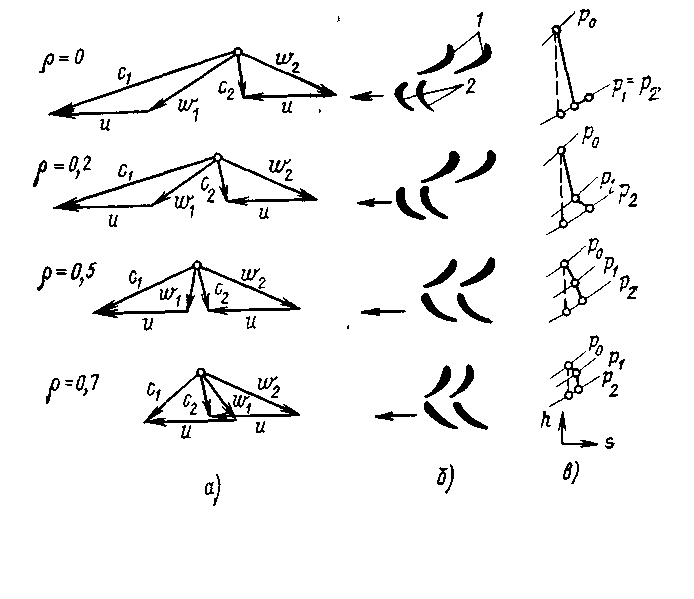






Рис 3.3 Треугольники скоростей (а), профили сопловых и рабочих лопаток (б) и h,s-диаграммы процессов (в) в турбинных ступенях с различной степенью реактивности:1,2-сопловые и рабочие лопатки
В осевых тур­бинных ступенях окружные скорости u₁ = u₂ = u. Отно­шение проходных сечений на выходах из сопловой и рабо­чей решеток зависит от сте­пени реактивности ступени. Проходное сечение решет­ки пропорционально sinα₁ или sinβ₁ (см. рис. 3.1, сечение A—A), а также длине l₁ или l₂ лопаток (см. рис. 3.1, а). Так, при степени реактивности ρ <0,5, если

1₁ = 1₂, то sinα₁<sinβ₂; если степень реактивности р=0,5, то sinα₁ = sinβ₂. При этом в обоих случаях отношения проходных сечений решеток различны. В за­висимости от степени реактивности и потерь энергии в рабочей решетке относительная скорость w₂ может быть больше или меньше скорости w₁ (см. рис. 3.3, а).

В криволинейных каналах рабочей решетки поворот и уско­рение струи пара происходят под влиянием действующих на нее усилий. Во-первых, пар испытывает реактивное усилие стенок канала, образованного рабочими лопатками. Во-вторых на него действует разность давлений р₁ и р₂ на входе и выходе из ре­шетки. Силы, действующие на рабочие лопатки при обтекании их паром, возникают вследствие поворота потока в каналах и его ускорении. Эти силы по своей природе являются дина­мическими.

Для их определения рас­смотрим поток пара в рабочей решетке (рис. 3.4), в котором выделим неподвижный контур-1—2—2'—1'—1, условно охва­тывающий одну рабочую ло­патку.



Рис 3.4 Схема потока пара в рабочей решетке
В действительности под этой лопаткой можно понимать все рабочие лопатки ступени. Линии 1—2 и 1'—2' конгруэнт­ны и расположены на одинако­вом расстоянии от соответству­ющих поверхностей соседних профилей лопаток, а линии 1—1' и 2—2' параллельны вектору окружной скорости и. На выделенную часть потока со стороны лопаток действует сила

реакции , а со стороны отброшенной части потока — силы давления на поверхности 1—1' и 2—2', 1—2 и 1'—2'. Так как силы давления на поверхностях 1—2 и 1'—2' равны и направлены противоположно, они взаимно урав­новешиваются.

Запишем уравнение количества движения (2.17) в векторной форме

. (3.2)

В этом уравнении первый член представляет собой импульс силы R', действующей со стороны лопаток на поток, а второй — импульс сил давления на поверхностях 1—1' и 2—2', площади которых обозначены Ω. В правой части уравнения записано из­менение количества движения элементарной массы пара dm, вытекающей через сечение 2—2' и втекающей через сечение 1— 1 за элементарное время dτ. Под Ω понимают площадь, описы­ваемую рабочими лопатками при движении в активном потоке рабочего тела. При полном подводе (парциальности е=1) пло­щадь Ω=πdl₂.

Поскольку dm/dτ=D — расход пара, запишем уравнение (3.2) в проекциях на направление окружной скорости:

. (3.3)

Заменив силу реакции R'_u лопаток силой R_u, с которой поток действует на них (R_u=-R'_u), получим уравнение для опреде­ления окружного усилия, действующего со стороны потока пара на рабочие лопатки турбинной ступени осевого типа:

. (3.4)

Поскольку направление окружного усилия R_u совпадает с направлением окружной скорости рабочих лопаток, этим усили­ем определяется работа, совершаемая потоком на рабочих ло­патках и соответственно на валу турбины.

З
(3.5)
аписав уравнение (3.2) в проекциях на направление осевой скорости, получим




(3.6)
Заменив силу реакции лопаток R'_a на усилие, с которым по­ток действует на них R_a = -R'_a, получим уравнение для опреде­ления осевого усилия, действующего со стороны потока пара на рабочие лопатки турбинной ступени осевого типа:



Это усилие направлено перпендикулярно вектору окружной скорости и, следовательно, не производит работы. Однако со­ставляющая R_a должна учитываться при расчете осевых усилий, воспринимаемых упорным подшипником ротора турбины.
3.2 Расчет и построение треугольников скоростей. Мощность и работа ступени