физика. Решение Для определения расстояния между минимумами в эксперименте Юнга можно использовать формулу d sin m, где d расстояние между отверстиями, длина волны света,
 Скачать 7.37 Mb. Скачать 7.37 Mb.
|
|
1-1. Разность хода лучей от двух когерентных источников света до некоторой точки на экране равна 1,36 мкм. Каков будет результат интерференции света в этой точке экрана, если длина волны света = 6709 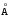 ? Решить этот же вопрос для длины волны ? Решить этот же вопрос для длины волны 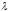 = 5360 = 5360 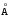 . . Решение: Результат интерференции света в точке экрана при заданной разности хода можно найти по формуле: I = 4I1I2cos^2(Δφ/2), где I1 и I2 - интенсивности света от каждого источника, Δφ - разность фаз между лучами, вызванная разностью хода. Для длины волны λ = 6709 А и разности хода 1,36 мкм нужно сначала вычислить соответствующую разность фаз: Δφ = 2πΔx/λ = 2π(1,36*10^-6 м)/6709*10^-10 м = 20π Тогда результат интерференции будет: I = 4I1I2cos^2(10π) = 4I1I2 Для длины волны λ = 5360 А аналогичным образом получаем: Δφ = 2πΔx/λ = 2π(1,36*10^-6 м)/5360*10^-10 м = 26π I = 4I1I2cos^2(13π) = 0 (т.к. cos(13π) = -1) 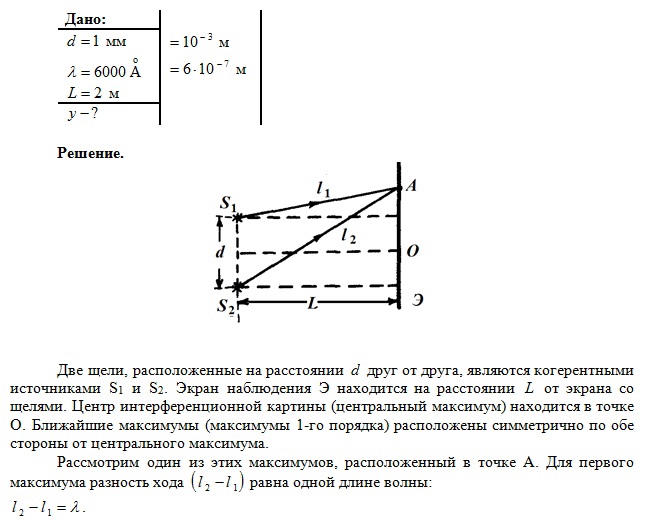  1-2. В непрозрачном экране на расстоянии 1 мм друг от друга сделаны две узкие параллельные щели, освещаемые монохроматическим светом с длиной волны 6000 1-2. В непрозрачном экране на расстоянии 1 мм друг от друга сделаны две узкие параллельные щели, освещаемые монохроматическим светом с длиной волны 6000 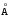 . По другую сторону экрана со щелями на расстоянии 2 м от него находится экран наблюдения. На каком расстоянии от центрального максимума наблюдаются два других ближайших максимума? . По другую сторону экрана со щелями на расстоянии 2 м от него находится экран наблюдения. На каком расстоянии от центрального максимума наблюдаются два других ближайших максимума?Решение: 1-3. В опыте Юнга отверстия освещались монохроматическим светом длиной волны 6000 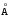 . Расстояние между отверстиями 1 мм и расстояние от отверстия до экрана 3 м. На каком расстоянии от центрального максимума находятся два ближайших минимума? Решение: Для определения расстояния между минимумами в эксперименте Юнга можно использовать формулу: d sinθ = mλ, где d - расстояние между отверстиями, λ - длина волны света, θ - угол между лучами света, проходящими через отверстия и пересекающимися на экране, m - порядковый номер минимума. . Расстояние между отверстиями 1 мм и расстояние от отверстия до экрана 3 м. На каком расстоянии от центрального максимума находятся два ближайших минимума? Решение: Для определения расстояния между минимумами в эксперименте Юнга можно использовать формулу: d sinθ = mλ, где d - расстояние между отверстиями, λ - длина волны света, θ - угол между лучами света, проходящими через отверстия и пересекающимися на экране, m - порядковый номер минимума. Для первого минимума m=1. sinθ = λ/d, θ = sin^(-1)(λ/d) Для нахождения расстояния между минимумами можно использовать следующее соотношение: y = L*tanθ, где y - расстояние между минимумами, L - расстояние от отверстий до экрана, θ - угол, определяемый из предыдущего выражения. y = L*tan(sin^(-1)(λ/d)) y = 3*tan(sin^(-1)(6000/1000)) y = 0.18 мм Ответ: два ближайших минимума находятся на расстоянии 0.18 мм от центрального максимума.  1-4. Во сколько раз изменится расстояние между соседними максимумами на экране в опыте Юнга, если зелёный светофильтр ( 1-4. Во сколько раз изменится расстояние между соседними максимумами на экране в опыте Юнга, если зелёный светофильтр (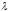 = 5000 = 5000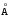 ) заменить красным светофильтром ( ) заменить красным светофильтром ( = 7000 = 7000  )? )?Решение: Замена. 1-5. Расстояние между четвертым и двадцать пятым темными кольцами Ньютона равно 9 мм. Радиус кривизны линзы 15 см. Найти длину волны света, падающего нормально на установку. Наблюдение производится в отражённом свете. Решение: Длина волны света, падающего нормально на установку, можно найти по формуле: λ = 2 * r * d / (n+1/2)^2, где r - радиус кривизны линзы, d - расстояние между темными кольцами (в нашем случае 9 мм), n - номер тёмного кольца (в нашем случае разность между номерами краевых кольца равна 20-4=16, а сами кольца нумеруются с 0, поэтому n=15). Подставляя значения, получаем: λ = 2 * 0.15 * 0.009 / (15+1/2)^2 ≈ 546 нм Ответ: длина волны света, падающего нормально на установку, составляет примерно 546 нм. 1-6. В установке для наблюдения колец Ньютона находится бензол (n = 1,33).Показатель преломления линзы и пластинки равен 1,6. Радиус кривизны линзы 2 м. Определить радиус третьего светлого кольца при наблюдении в отражённом свете с длиной волны 6000  . .Решение: Ответ: длина волны света, падающего нормально на установку, составляет примерно 546 нм.  . .Решение: Для определения радиуса третьего светлого кольца нужно воспользоваться формулой для радиусов светлых колец Ньютона в отражённом свете: (1 уравнение) где n - показатель преломления среды (в данном случае бензол), λ - длина волны света, R - радиус кривизны линзы, rn - радиус n-го светлого кольца. Подставляя данные из условия, получаем: (2 уравнение) Ответ: радиус третьего светлого кольца при наблюдении в отражённом свете с длиной волны 6000 Å равен примерно 0,194 мм.  1-7. Кольца Ньютона наблюдаются в отражённом свете с длиной волны 5890 1-7. Кольца Ньютона наблюдаются в отражённом свете с длиной волны 5890  . В некоторой точке толщина воздушного слоя между линзой и пластиной равна 1,767 мкм. Какое кольцо светлое или тёмное будет проходить через эту точку? Найти также номер кольца. . В некоторой точке толщина воздушного слоя между линзой и пластиной равна 1,767 мкм. Какое кольцо светлое или тёмное будет проходить через эту точку? Найти также номер кольца.Решение: При наблюдении Колец Ньютона в отражённом свете темным кольцом называют кольцо, в котором разность хода между отражёнными лучами равна нечётному числу полуволн. Светлое кольцо соответствует чётному числу полуволн разности хода. Для определения номера кольца используется формула: m = (2*t*m)/(λ*n) + (1/2), где t - толщина воздушного слоя, m - номер кольца, λ - длина волны света, n - показатель преломления стекла. В данном случае: t = 1,767 мкм = 1,767*10^-6 м, λ = 5890 A = 5890*10^-10 м, n = 1,5 (для стекла). Для тёмного кольца разность хода между отражёнными лучами должна быть равна (2*m - 1/2)*λ, т.е. (2*m - 1/2)*λ = 2*t*m, откуда m = (2*t)/(2*λ - λ/2) = 147. Таким образом, через данную точку пройдёт тёмное кольцо с номером 147. 1-8. Мыльная плёнка толщиной 0,3 мкм освещается белым светом под углом падения 0 и рассматривается в отражённых лучах. Каким цветом будет при этом окрашена плёнка, если показатель преломления плёнки n = 1,33? Решение:  1-9. При какой наименьшей толщине мыльной плёнки она представляется зелёной ( 1-9. При какой наименьшей толщине мыльной плёнки она представляется зелёной ( = 5000 = 5000  ) при наблюдении её в отражённом свете под углом падения 0, если для плёнки n = 1,33. ) при наблюдении её в отражённом свете под углом падения 0, если для плёнки n = 1,33.Решение: Замена.   1-10. Мыльная плёнка толщиной 0,5 мкм освещается белым светом под углом падения 300. Каким цветом будет окрашена плёнка в отражённых лучах, если для плёнки n = 1,33. 1-10. Мыльная плёнка толщиной 0,5 мкм освещается белым светом под углом падения 300. Каким цветом будет окрашена плёнка в отражённых лучах, если для плёнки n = 1,33.Решение: 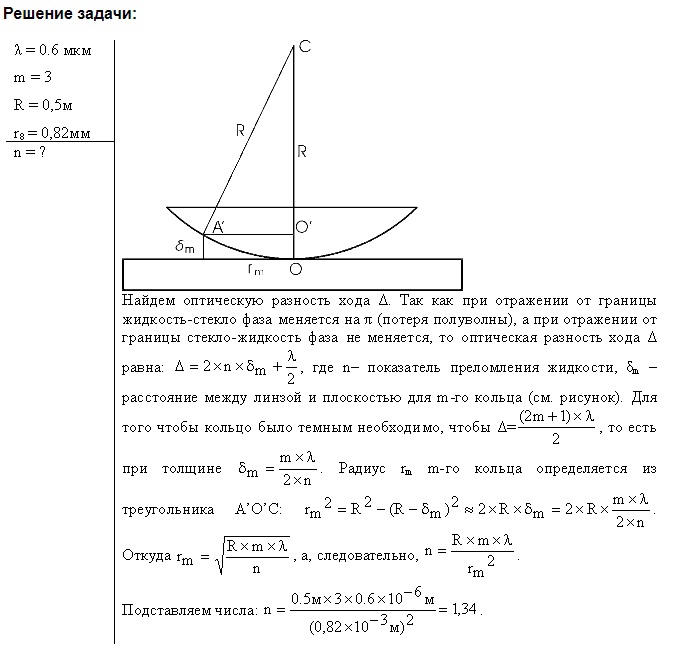  1-11. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего тёмного кольца Ньютона при наблюдении в отражённом свете с длиной волны 1-11. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего тёмного кольца Ньютона при наблюдении в отражённом свете с длиной волны 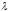 = 0,6 мкм равен 0,82 мм. Радиус кривизны линзы R = 0,5 м. = 0,6 мкм равен 0,82 мм. Радиус кривизны линзы R = 0,5 м.Решение:   1-12. На тонкую плёнку нормально к её поверхности падает монохроматический свет с длиной волны 1-12. На тонкую плёнку нормально к её поверхности падает монохроматический свет с длиной волны 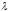 = 500 нм. Отражённый от неё свет максимально усилен вследствие интерференции. Определить минимальную толщину dmin плёнки, если показатель преломления материала плёнки равен 1,4. = 500 нм. Отражённый от неё свет максимально усилен вследствие интерференции. Определить минимальную толщину dmin плёнки, если показатель преломления материала плёнки равен 1,4.Решение: 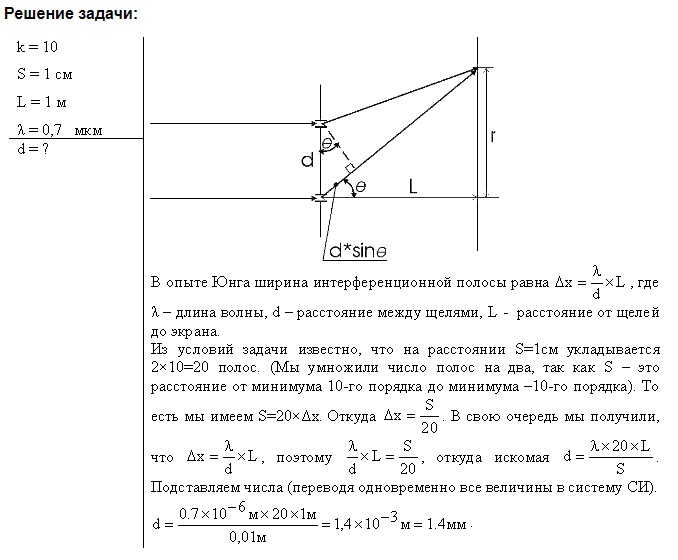  1-13. Расстояние L от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние d между щелями, если на отрезке длиной l = 1 см укладывается N=10 темных интерференционных полос. Длина волны 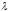 = 0,7 мкм. = 0,7 мкм.Решение:  1-14. На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны  = 500 нм. Найти радиус R линзы, если радиус четвёртого светлого кольца Ньютона в отражённом свете равен 2 мм. = 500 нм. Найти радиус R линзы, если радиус четвёртого светлого кольца Ньютона в отражённом свете равен 2 мм.Решение:  1-15. На тонкую глицериновую плёнку толщиной d = 1,5 мкм нормально к её поверхности падает белый свет. Определить длины волн  лучей видимого участка спектра (0,4 мкм лучей видимого участка спектра (0,4 мкм    0,8 мкм), которые будут ослаблены в результате интерференции. 0,8 мкм), которые будут ослаблены в результате интерференции.Решение: Для вычисления длин волн, которые будут ослаблены в результате интерференции на тонкой плёнке, необходимо использовать формулу: 2d(m + ½) = mλ, где d - толщина плёнки, λ - длина волны света, m - целое число. Подставляя значения, получаем: 2 × 1,5 × 10^-6 × (m + ½) = mλ. Для первого минимума интерференции (m = 0) получаем: λ = 2d/2(n + ½) = 2 × 1,5 × 10^-6/2(0 + ½) = 750 нм. Для второго минимума интерференции (m = 1) получаем: λ = 2d/2(n + ½) = 2 × 1,5 × 10^-6/2(1 + ½) = 500 нм. Таким образом, длины волн 500 нм и 750 нм будут ослаблены в результате интерференции на тонкой глицериновой плёнке. 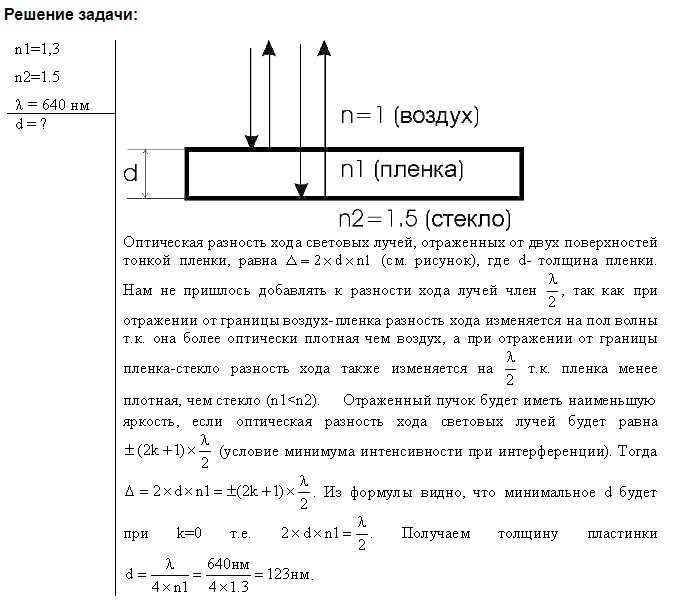   1-16. На стеклянную пластинку нанесён тонкий слой прозрачного вещества с показателем преломления n = 1,3. Пластинка освещается параллельными лучами с длиной волны 1-16. На стеклянную пластинку нанесён тонкий слой прозрачного вещества с показателем преломления n = 1,3. Пластинка освещается параллельными лучами с длиной волны 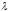 = 640 нм, падающими на пластинку нормально. Какую минимальную толщину d должен иметь слой, чтобы отражённые лучи имели наименьшую яркость? = 640 нм, падающими на пластинку нормально. Какую минимальную толщину d должен иметь слой, чтобы отражённые лучи имели наименьшую яркость?Решение:  1-17. На тонкий стеклянный клин падают нормально лучи с длиной волны 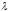 = 500 нм. Расстояние между соседними темными интерференционными полосами в отражённом свете b = 0,5 мм. Определить угол между поверхностями клина. Показатель преломления стекла клина n = 1,6. = 500 нм. Расстояние между соседними темными интерференционными полосами в отражённом свете b = 0,5 мм. Определить угол между поверхностями клина. Показатель преломления стекла клина n = 1,6. Решение:    1-18. Плосковыпуклая линза с фокусным расстоянием F = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого кольца Ньютона в отражённом свете равен 1,1 мм. Определить длину световой волны 1-18. Плосковыпуклая линза с фокусным расстоянием F = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого кольца Ньютона в отражённом свете равен 1,1 мм. Определить длину световой волны 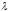 . .Решение:    1-19. На пути света поставлена стеклянная пластина толщиной d = 1 мм так, что угол падения луча равен 30. На сколько изменится оптическая длина пути луча? Решение: 1-20. На мыльную плёнку с показателем преломления n = 1,33 падает нормально монохроматический свет с длиной волны 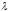 = 0,6 мкм. Отражённый свет в результате интерференции имеет наибольшую яркость. Определить наименьшую толщину плёнки. = 0,6 мкм. Отражённый свет в результате интерференции имеет наибольшую яркость. Определить наименьшую толщину плёнки.Решение: Наименьшая толщина плёнки будет равна половине длины волны в среде плёнки, умноженной на коэффициент преломления: t = λ/(2n) = 0,6 мкм/(2*1,33) ≈ 0,225 мкм. Ответ: наименьшая толщина плёнки равна примерно 0,225 мкм. 1-21. Радиус второго тёмного кольца Ньютона в отражённом свете r = 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны 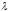 = 0,64 мкм. = 0,64 мкм.Решение: Для решения этой задачи необходимо использовать формулу для радиуса n-ого тёмного кольца в отражённом свете: r_n = √(n * λ * f), где λ - длина волны света, f - фокусное расстояние линзы. Мы знаем радиус второго тёмного кольца в отражённом свете r = 0,4 мм и длину волны света λ = 0,64 мкм. Для определения радиуса кривизны линзы необходимо найти фокусное расстояние f. Для второго тёмного кольца n=2, поэтому: r_2 = √(2 * λ * f), f = r_2^2 / (2 * λ) = 0,4^2 / (2 * 0,64 * 10^-6) = 125000 мкм = 0,125 мм. Таким образом, радиус кривизны плосковыпуклой линзы равен 0,125 мм. Решение: Для определения длины волны падающего света можно использовать формулу для радиусов темных колец Ньютона: (1 уравнение), где rn- радиус n-го кольца, λ - длина волны света, R- радиус кривизны линзы. Из условия задачи известны диаметры девятого и двенадцатого темных колец Ньютона: (2 и 3 уравнение) Радиусы этих колец можно найти, разделив диаметры на 2: (4 и 5 уравнение) Разделив второе уравнение на первое, получаем: (8, 9 и 10 уравнение) Отсюда: (13 уравнение) В |
