физика. Решение Для определения расстояния между минимумами в эксперименте Юнга можно использовать формулу d sin m, где d расстояние между отверстиями, длина волны света,
 Скачать 7.37 Mb. Скачать 7.37 Mb.
|
|
Решение: 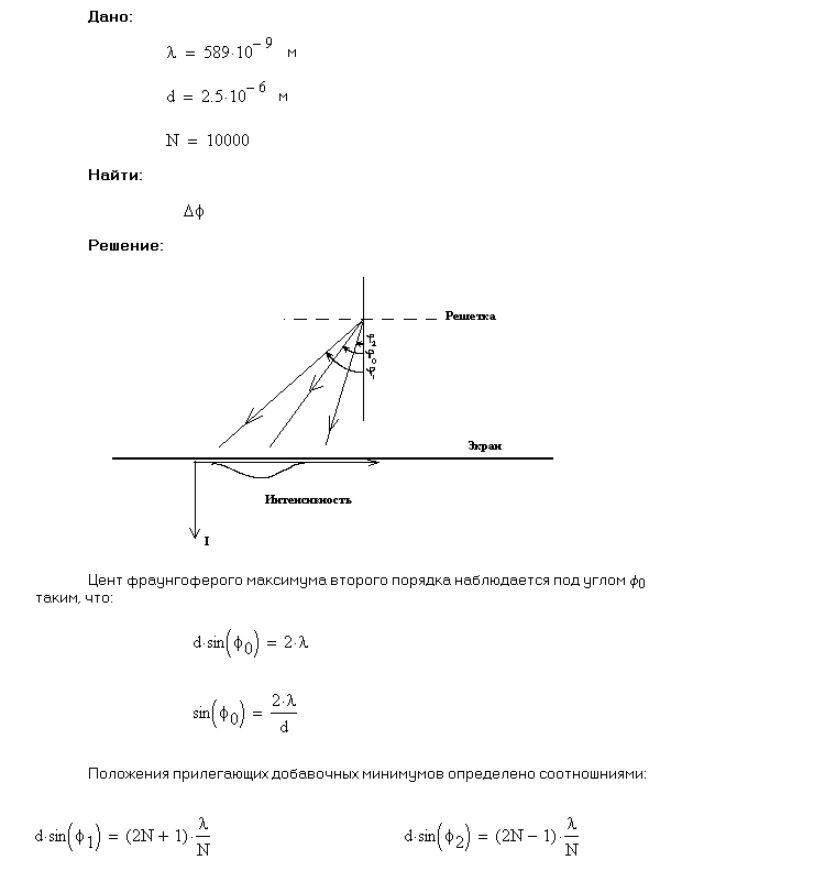      1-45. Определить ширину спектральной линии водорода, длина волны которой 0,656 мкм в спектре первого порядка, даваемого решёткой длиной 4 см. Фокусное расстояние линзы, проецирующей спектр на экран, равняется 20 см. Ширина спектральной линии – это расстояние между двумя минимумами, лежащими рядом с этой линией. 1-45. Определить ширину спектральной линии водорода, длина волны которой 0,656 мкм в спектре первого порядка, даваемого решёткой длиной 4 см. Фокусное расстояние линзы, проецирующей спектр на экран, равняется 20 см. Ширина спектральной линии – это расстояние между двумя минимумами, лежащими рядом с этой линией.Решение: Замена. 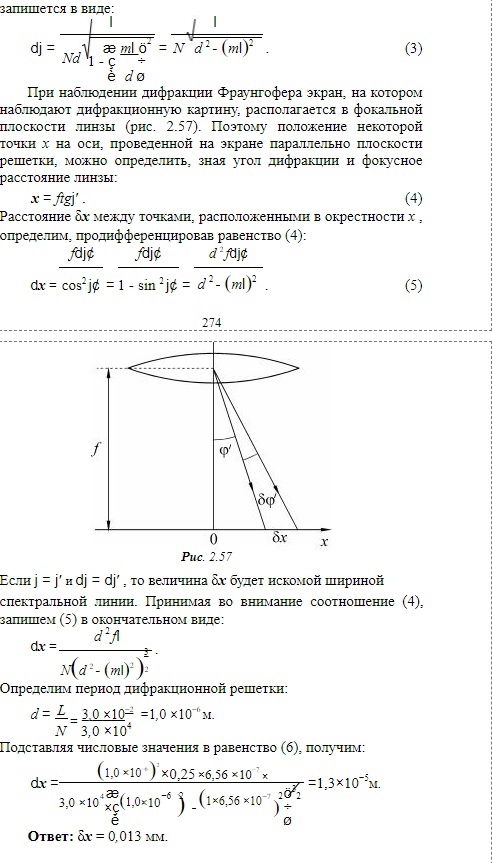    1-46. Сравнить разрешающие способности двух дифракционных решёток, если одна из них имеет 420 штрихов на 1 мм при ширине 2 см, а вторая содержит 720 штрихов на 1 мм при ширине решётки 4,8 см. Решение: Разрешающая способность дифракционной решётки определяется формулой: d*sin(θ) = m*λ, где d - расстояние между штрихами, θ - угол дифракции, m - порядок дифракционного максимума, λ - длина волны света. Для решётки с 420 штрихами на 1 мм и шириной 2 см расстояние между штрихами можно вычислить: d = 1 / 420 мм/штрих = 2,38*10^-6 м/штрих. Ширина решётки в метрах: L = 2 см = 0,02 м. Разрешающая способность для этой решётки будет максимальной при максимальном порядке дифракционного максимума m = 1, при этом угол дифракции можно оценить как: sin(θ) ≈ θ = λ/d = 500 нм / 2,38*10^-6 м/штрих = 0,21 рад. Ширина дифракционной картины: Δx ≈ L*θ = 0,02 м * 0,21 рад = 0,0042 м = 4,2 мм. Для решётки с 720 штрихами на 1 мм и шириной 4,8 см расстояние между штрихами можно вычислить: d = 1 / 720 мм/штрих = 1,39*10^-6 м/штрих. Ширина решётки в метрах: L = 4,8 см = 0,048 м. Разрешающая способность для этой решётки будет максимальной при максимальном порядке дифракционного максимума m = 1, при этом угол дифракции можно оценить как: sin(θ) ≈ θ = λ/d = 500 нм / 1,39*10^-6 м/штрих = 0,36 рад. Ширина дифракционной картины: Δx ≈ L*θ = 0,048 м * 0,36 рад = 0,017 м = 1,7 см. Таким образом, разрешающая способность второй решётки выше, чем у первой, поскольку ширина дифракционной картины для второй решётки меньше. 1-47. Каково наименьшее значение диаметра телескопа, который может разрешить дифракционные изображения двух звёзд, если угловое расстояние между ними 2΄΄? Глаз наиболее чувствителен к длине волны 5500  . .Решение: Минимальный диаметр телескопа, который может разрешить дифракционные изображения двух звёзд с угловым расстоянием 2" и длиной волны 5500 Å, можно вычислить с помощью формулы Рэлея: D = 1,22 λ / θ, где D - диаметр телескопа, λ - длина волны света, а θ - угловое расстояние между звёздами. Подставляя значения, получаем: D = 1,22 * 5500 Å / 2" = 16 м. Таким образом, минимальный диаметр телескопа составляет 16 метров. 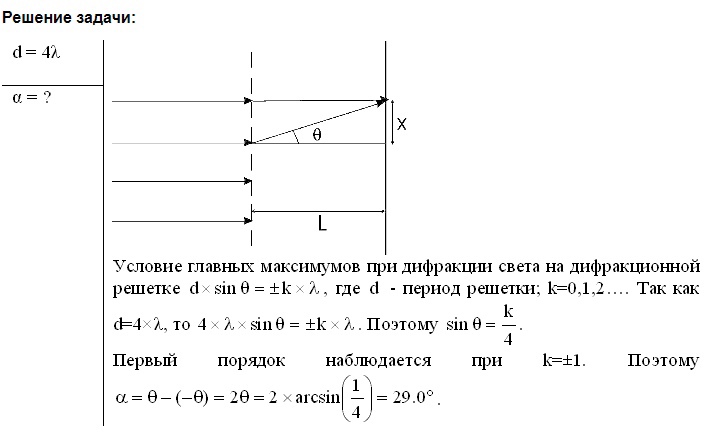   1-48. Постоянная дифракционной решётки в n = 4 раза больше длины световой волны монохроматического света, нормально падающего на её поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами. 1-48. Постоянная дифракционной решётки в n = 4 раза больше длины световой волны монохроматического света, нормально падающего на её поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами. Решение: 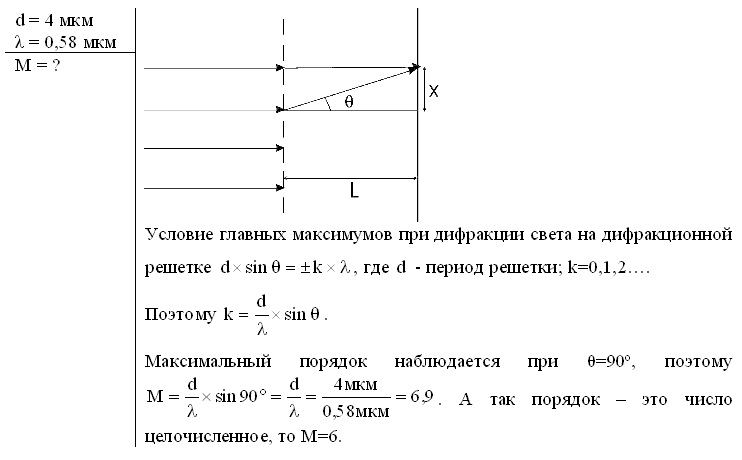   1-49. Расстояние между штрихами дифракционной решётки d = 4 мкм. На решётку падает нормально свет с длиной волны = 0,58 мкм. Максимум какого наибольшего порядка даёт эта решётка? 1-49. Расстояние между штрихами дифракционной решётки d = 4 мкм. На решётку падает нормально свет с длиной волны = 0,58 мкм. Максимум какого наибольшего порядка даёт эта решётка?Решение:    1-50. Какое наименьшее число штрихов должна содержать решётка, чтобы в спектре второго порядка можно было видеть раздельно две жёлтые линии натрия с длиной волны = 589,0 нм и = 589,6 нм? Какова длина l такой решётки, если расстояние между штрихами b = 5 мкм? 1-50. Какое наименьшее число штрихов должна содержать решётка, чтобы в спектре второго порядка можно было видеть раздельно две жёлтые линии натрия с длиной волны = 589,0 нм и = 589,6 нм? Какова длина l такой решётки, если расстояние между штрихами b = 5 мкм?Решение:   Решение: 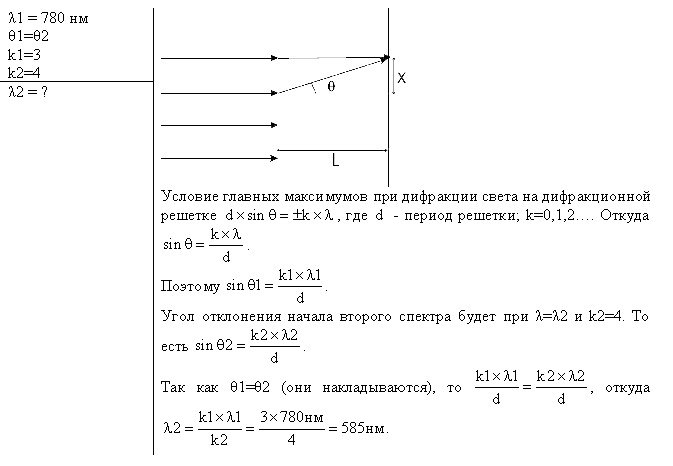   1-52. На дифракционную решётку падает нормально параллельный пучок лучей белого света. Спектры третьего и четвёртого порядков частично накладываются друг на друга. На какую длину волны в спектре четвёртого порядка накладывается граница ( = 780 нм) спектра третьего порядка? 1-52. На дифракционную решётку падает нормально параллельный пучок лучей белого света. Спектры третьего и четвёртого порядков частично накладываются друг на друга. На какую длину волны в спектре четвёртого порядка накладывается граница ( = 780 нм) спектра третьего порядка?Решение:    1-53. На дифракционную решётку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проектируется помещённой вблизи решётки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра: = 780нм, =400 нм. 1-53. На дифракционную решётку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проектируется помещённой вблизи решётки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра: = 780нм, =400 нм.Решение:  1-54. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей. Расстояние между атомными плоскостями кристалла d = 280 пм. Под углом = 65 к плоскости грани наблюдается дифракционный максимум первого порядка. Определить длину волны 1-54. На грань кристалла каменной соли падает параллельный пучок рентгеновских лучей. Расстояние между атомными плоскостями кристалла d = 280 пм. Под углом = 65 к плоскости грани наблюдается дифракционный максимум первого порядка. Определить длину волны  рентгеновских лучей. рентгеновских лучей.Решение:    1-55. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна ( = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, равен 20. Определить ширину a щели. 1-55. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна ( = 600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, равен 20. Определить ширину a щели.Решение: 1-56. На пластину со щелью, ширина которой а = 0,05 мм, падает нормально монохроматический свет с длиной волны = 0,7 мкм. Определить угол отклонения лучей, соответствующих первому дифракционному максимуму. Решение: Угол отклонения лучей первого дифракционного максимума можно определить с помощью формулы: sin(φ) = λ / a, где λ - длина волны света, a - ширина щели. Подставляя значения, получаем: sin(φ) = 0,7 мкм / 0,05 мм = 14 Ответ: угол отклонения лучей первого дифракционного максимума равен примерно 14 градусам. 1-57. Дифракционная решётка, освещённая нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол = 30. На какой угол отклоняет она спектр четвёртого порядка? Решение: Для дифракционной решётки, отклоняющей спектр третьего порядка на угол φ = 30 градусов, угол отклонения спектра четвёртого порядка можно найти с помощью формулы: sin(θ4) = (4/3)sin(θ3), где θ4 - угол отклонения спектра четвёртого порядка, θ3 - угол отклонения спектра третьего порядка. Подставив значения, получим: sin(θ4) = (4/3)sin(30 градусов) = 0.8, θ4 = sin^(-1)(0.8) = 53.1 градусов. Таким образом, дифракционная решётка отклоняет спектр четвёртого порядка на угол 53.1 градусов. 1-58. При расширении круглого отверстия от одной до двух зон Френеля освещённость в центре экрана падает почти до нуля. Как согласовать этот факт с увеличением светового потока в два раза? Решение: Увеличение светового потока в два раза может произойти при увеличении диаметра источника света в четыре раза. Однако при расширении круглого отверстия от одной до двух зон Френеля, световой поток не увеличивается в четыре раза, а распределяется по более широкой области, что приводит к уменьшению интенсивности света в центре экрана. Это объясняется интерференцией световых волн, создаваемых различными участками источника света, которые могут быть в фазе или противофазе в разных точках на экране. 1-59. Какова интенсивность света в центре дифракционной картины от диска, если он закрывает две зоны Френеля? Интенсивность света в отсутствие препятствия равна I0. Описать изменение дифракционной картины при увеличении поперечных размеров диска. Решение: Интенсивность света в центре дифракционной картины от диска, который закрывает две зоны Френеля, будет равна половине от исходной интенсивности I0. При увеличении поперечных размеров диска, размеры зон Френеля, закрываемых диском, также увеличиваются. Это приводит к уменьшению числа зон Френеля, которые закрывает диск, и, следовательно, к уменьшению числа интерференционных полос в дифракционной картине. При достаточно большом размере диска дифракционная картина становится более простой и похожей на тень от препятствия. 1-60. На щель, ширина которой а = 6103 мм, нормально падает свет с длиной волны 7000  . Найти углы, по направлению которых будут наблюдаться максимумы и минимумы света 1-го порядка. Что произойдёт со спектром, если образовать решётку с периодом 2а? . Найти углы, по направлению которых будут наблюдаться максимумы и минимумы света 1-го порядка. Что произойдёт со спектром, если образовать решётку с периодом 2а?Решение: Для решения задачи используем формулу дифракции Фраунгофера: sinθ = mλ/d, где θ - угол между направлением падающего света и направлением на максимумы или минимумы, m - порядок интерференции, λ - длина волны света, d - расстояние между щелями решётки. Для одной щели, расстояние между "щелями" равно ширине щели d=a=6*10^-3 мм. Для максимума первого порядка (m=1): sinθ = λ/d = 7000 Å / 6*10^-3 мм = 1.17, θ = arcsin(1.17) = 70.5° Для минимума первого порядка (m=1): sinθ = λ/d = 7000 Å / 6*10^-3 мм = 1.17, θ = arcsin(1.17) = 70.5° Если образовать решётку с периодом 2*a, расстояние между "щелями" будет равно d=2*a=12*10^-3 мм. Тогда максимумы и минимумы будут наблюдаться под углами: Для максимума первого порядка (m=1): sinθ = λ/d = 7000 Å / 12*10^-3 мм = 0.58, θ = arcsin(0.58) = 35.2°, Для минимума первого порядка (m=1): sinθ = λ/d = 7000 Å / 12*10^-3 мм = 0.58, θ = arcsin(0.58) = 35.2° Таким образом, при увеличении расстояния между "щелями" расстояние между максимумами и минимумами уменьшается, а углы, под которыми они наблюдаются, увеличиваются. (ред.) 1-61. Определить период дифракционной решётки, которая даёт в спектре первого порядка на экране, отстоящем от решётки на 5 м, линии натрия с = 5890 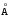 и = 5896 и = 5896 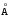 на расстоянии 0,5 мм друг от друга. на расстоянии 0,5 мм друг от друга.Решение: Используя формулу для дифракционной решётки: d*sin(θ) = m*λ, где d - период решётки, θ - угол между направлением луча и нормалью к решётке, m - порядок дифракционной картины, λ - длина волны света. Первая линия натрия имеет длину волны λ1 = 5890 А, а вторая линия натрия имеет длину волны λ2 = 5896 А. Разность между этими длинами волны равна: Δλ = λ2 - λ1 = 6 А = 6*10^(-7) метров. Чтобы найти период решётки, нужно найти угол θ, подставив значения в формулу для m=1: d*sin(θ) = λ1, sin(θ) = λ1/d, θ = sin^(-1)(λ1/d) Теперь мы можем найти расстояние между линиями на экране, используя формулу для междуоптического расстояния: y = L*tan(θ) + (Δλ/d)*L, где L - расстояние от решётки до экрана, y - расстояние между линиями на экране. Подставляя значения, получаем: y = 5*tan(sin^(-1)(λ1/d)) + (Δλ/d)*5, y = 5*(λ1/d) + (Δλ/d)*5. Теперь мы можем найти период решётки, используя формулу: d = Δλ/y. Подставляя значения, получаем: d = (6*10^(-7)) / (0,5*10^(-3)), d = 1,2*10^(-3) метров или 1,2 мм. 1-62. Чем определяется максимальный порядок спектра и максимальная длина волны при дифракции на заданной решётке? Решение: Максимальный порядок спектра определяется формулой nmax = d / λ, где d - период решётки, λ - длина волны света. Максимальная длина волны при дифракции на заданной решётке определяется формулой λmax = 2d / nmin, где nmin - минимальный порядок спектра. 1-63. Найти наибольший порядок для жёлтой линии натрия = 5890 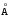 , если дифракционная решётка имеет на 1 мм 500 штрихов. , если дифракционная решётка имеет на 1 мм 500 штрихов.Решение: Длина волны жёлтой линии натрия λ = 5890 Å. Расстояние между штрихами решётки d = 1 мм / 500 = 0.002 мм = 2 x 10^-6 м. Наибольший порядок дифракции может быть найден с помощью уравнения: d sin θ = m λ, где θ - угол дифракции, m - порядок дифракции. Для нахождения наибольшего порядка, мы можем использовать условие, что sin θ = 1: d = m λ / sin θ, m = d sin θ / λ = 1 / (λ/d) = 1 / (5890 x 10^-10 / 2 x 10^-6) = 33.33 Таким образом, наибольший порядок для жёлтой линии натрия равен 33.   1-64. Определить разрешающую силу дифракционной решётки с периодом 0,01 см1 и длиной 5 см в спектрах 1 и 3-го порядков. Изменится ли разрешающая сила при изменении наклона, падающего на решётку света? 1-64. Определить разрешающую силу дифракционной решётки с периодом 0,01 см1 и длиной 5 см в спектрах 1 и 3-го порядков. Изменится ли разрешающая сила при изменении наклона, падающего на решётку света?Решение: 1-65. Найти минимальное число штрихов решётки, которая может разрешить натриевый дуплет ( =5890 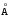 и = 5986 и = 5986  ) в спектре 1-го порядка. ) в спектре 1-го порядка.Решение: Минимальное число штрихов решётки (N) можно найти с помощью формулы: N = λ / Δλ, где λ - длина волны, Δλ - разрешающая способность решётки. Для натрия-вого дуплета разрешающая способность решётки будет зависеть от её параметров, таких как количество штрихов (N) и ширина штриха (d). Однако, если мы предположим, что ширина штриха равна длине волны (λ), то мы можем использовать формулу для разрешающей способности Давида-Брюстера: Δλ = λ / N Теперь мы можем выразить минимальное число штрихов решётки: N = λ / Δλ = λ / (λ / N) = N, N = 5890 Å / 96 Å ≈ 61, N = 5986 Å / 96 Å ≈ 62 Таким образом, минимальное число штрихов решётки, которая может разрешить натриевый дуплет в спектре 1-го порядка, составляет примерно 61-62 штриха.  и расстоянии от решётки до экрана 0,5 м. и расстоянии от решётки до экрана 0,5 м.Решение: Угловая дисперсия решётки может быть рассчитана с использованием уравнения: Угловая дисперсия решётки может быть рассчитана с использованием уравнения: (1 уравнение) ,где d - период решётки, - угол отклонения, m - порядок интерференции, λ - длина волны света. 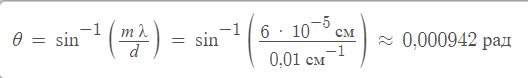 Решётка имеет период d = 0,01 см^-1. Для спектра первого порядка, порядок интерференции m = 1. Длина волны (2 уравнение) Решётка имеет период d = 0,01 см^-1. Для спектра первого порядка, порядок интерференции m = 1. Длина волны (2 уравнение)Т огда угол отклонения равен: 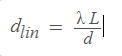 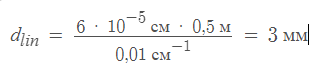 Линейная дисперсия определяется как расстояние между двумя соседними максимумами на экране: (3 уравнение), где L- расстояние от решётки до экрана. Линейная дисперсия определяется как расстояние между двумя соседними максимумами на экране: (3 уравнение), где L- расстояние от решётки до экрана.Подставляя значения, получаем: (4 и 5 уравнение) Таким образом, угловая дисперсия решётки равна примерно 0,000942 рад, а линейная дисперсия равна примерно 3 мм. 1-67. Угол падения рентгеновских лучей на естественную грань монокристалла хлористого натрия плотностью 2,16 г/см3 равен 30. Определить длину волны излучения, если при зеркальном отражении от этой грани образуется максимум второго порядка. |
