2870538 МОР, В-25. Решение Для запрета перемещения в x 12 устанавливаем для этой ячейки более высокое значение M
 Скачать 58.02 Kb. Скачать 58.02 Kb.
|
РешениеПредполагаем, что игрок I выбирает такую стратегию, при которой полученный выигрыш будет максимальным. Игрок II выбирает такую стратегию, чтобы минимизировать выигрыш игрока I. Определим минимальные значения для каждого А и максимальные – для каждого В. Получим:
Гарантированный выигрыш определяется нижней ценой игры. Согласно методу минимакса, нижней ценой игры является максимальное значение из минимальных a, то есть: max(Ai)=4. Верхней ценой игры является минимальное значение из максимальных значений B: min(bj) = 4. Так как max(Ai)= min(bj)=4, седловая точка существует и указывает решение на пару альтернатив (A3, B2). Таким образом, цена игры равна 4. 3. Определить оптимальные стратегии игроков и найти среднюю цену игры, применив графический и аналитический методы решения: 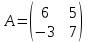 Решение Проверим, имеет ли матрица седловую точку.
Гарантированный выигрыш, определяемый нижней ценой игры равен максимальному значению a, то есть 5, которая указывает на максимальную чистую стратегию A1. Верхняя цена игры – минимальное значение из b - составляет 6.  седловая точка отсутствует. седловая точка отсутствует.Цена игры находится в пределах 5 ≤ y ≤ 6. Это значит, что решение игры ищем в смешанных стратегиях: игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш, а игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I. Решим задачу графическим методом. Для этого на осях отложим единичный отрезок. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2). На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2. Решение игры (2 x 2) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет. Выделяем нижнюю границу выигрыша B1NB2. Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B1B1 и B2B2, для которых можно записать следующую систему уравнений: y = 6 + (-3 - 6)p2 y = 5 + (7 - 5)p2 Откуда p1 = 10/11 p2 = 1/11 Цена игры, y = 57/11 Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений 6q1+5q2 = y -3q1+7q2 = y q1+q2 = 1 или 6q1+5q2 = 57/11 -3q1+7q2 = 57/11 q1+q2 = 1 Решая эту систему, находим: q1 = 2/11; q2 = 9/11. Таким образом, цена игры равна y = 57/11, векторы стратегии игроков: Q(2/11, 9/11), P(10/11, 1/11)  4. Найти решение игры путем сведения ее к задаче линейного программирования:  Решение Для начала проверим, имеет ли платежная матрица седловую точку.
Нижняя цена игры, характеризующая гарантированный выигрыш, составит: a = max(ai) = 1 Верхняя цена игры: b = min(bj) = 2 Получим: a ≠ b – седловая точка отсутствует, решение найдем в смешанных стратегиях. Цена игры будет заключена в интервале 1 ≤ y ≤ 2. Запишем математические модели пары двойственных задач линейного программирования. Минимум функции F(x) при ограничениях (для игрока II): 4x1+3x2 ≥ 1 2x1+x2+2x3 ≥ 1 4x2+2x3 ≥ 1 F(x) = x1+x2+x3 → min Максимум функции Z(y) при ограничениях (для игрока I): 4y1+2y2 ≤ 1 3y1+y2+4y3 ≤ 1 2y2+2y3 ≤ 1 Z(y) = y1+y2+y3 → max Решим прямую задачу линейного программирования двойственным симплексным методом, с использованием симплексной таблицы. Приведем систему ограничений к системе неравенств смысла ≤, умножив соответствующие строки на (-1). Определим минимальное значение целевой функции F(X) = x1+x2+x3 при следующих условиях-ограничений. -4x1-3x2≤-1 -2x1-x2-2x3≤-1 -4x2-2x3≤-1 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). -4x1-3x2+x4 = -1 -2x1-x2-2x3+x5 = -1 -4x2-2x3+x6 = -1 Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,-1,-1,-1)
План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 1-ая строка, а переменную x4 следует вывести из базиса. Минимальное значение θ соответствует 1-му столбцу, т.е. переменную x1 необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-4).
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
|
