2870538 МОР, В-25. Решение Для запрета перемещения в x 12 устанавливаем для этой ячейки более высокое значение M
 Скачать 58.02 Kb. Скачать 58.02 Kb.
|
|
План 1 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 3-ая строка, а переменную x6 следует вывести из базиса. Минимальное значение θ соответствует 2-му столбцу, т.е. переменную x2 необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент, равный (-4).
Выполняем преобразования симплексной таблицы.
План 2 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 2-ая строка, а переменную x5 следует вывести из базиса. Минимальное значение θ соответствует 3-му столбцу, т.е. переменную x3 необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент, равный (-21/4).
Выполним преобразования симплексной таблицы.
В базисном столбце все элементы положительные, следовательно, переходим к основному алгоритму симплекс-метода. Индексная строка не содержит положительных элементов – это значит, что найден оптимальный план. Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: 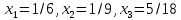 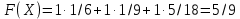 Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи: y1=-1/18, y2=-7/18, y3=-1/9 5. Необходимо распределить средства в размере S0 в течении n лет между двумя предприятиями. Средства x, выделяемые 1 предприятию, приносят в конце года доход f1(x) и возвращаются в размере 1(x) 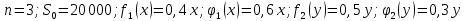 Решение Выведем выражения для показателей эффективности шага k: 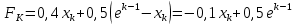 Уравнение состояния: 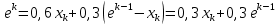 Перейдем к выведению реккурентных соотношений Беллмана и запишем их следующим образом: 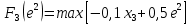 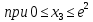 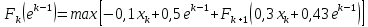 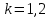 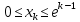 Проведем этап условной оптимизации. 3-й шаг: 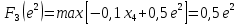 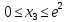 Показатель эффективности F3(e2) – линейная функция относительно x3. Эта переменная входит в выражение со знаком минус, то F3(e2) достигает максимума в конце интервала 0 ≤ x3 ≤ e2, т.е. при x3 = e2. 2-й шаг: 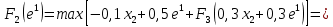 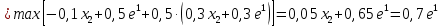 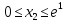 Показатель эффективности F2(e1) – линейная функция относительно x2. Эта переменная входит в выражение со знаком плюс, то F2(e1) достигает максимума в начале интервала 0 ≤ x2 ≤ e1, т.е. при x2 = 0. 1-й шаг: 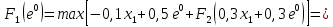 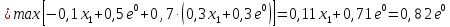 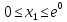 Показатель эффективности F1(e0) – линейная функция относительно x1. Эта переменная входит в выражение со знаком плюс, то F2(e1) достигает максимума в начале интервала 0 ≤ x1 ≤ e0, т.е. при x1 = e0. Перейдем к этапу безусловной оптимизации: e0 = 20000: Fmax = F1(e0) = 16400, x1 = 0 e0 = 20000: e1 = 0,3∙20000 + 0,3∙20000 = 12000, x1 = e0 e1 = 12000, то e2 = 0,3∙0 + 0,3∙20000 = 12000, x2 = e1 e2 = 7200, то e3 = 0,3∙0 + 0,3∙7200 = 2160, x3 = 0 Получим следующее распределение средств по годам и предприятиям:
6. Планируется работа трех предприятий на 1 год. Начальные средства равны s0 = 4 тыс. у.е., а вложения кратны 1 тыс. у.е. При этом x тыс. у.е., вложенные в k-е предприятие в начале года, дают в конце года прибыль fK(x). Определить оптимальный план распределения средств и найти максимальную прибыль.
Решение Отдельным шагом задачи считается выделение средств очередному предприятию, переменные управления ui (i=1,2,3) представляют собой сумму средств, выделенных i-му предприятию. Задача оптимизации | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
