Кондратьев А.С. МЕХАНИКА ЖИДКОСТИ И ГАЗА. Решение Формула увеличения обьема жидкости при нагревании Формула изменения обьема при сжатии
 Скачать 27.8 Kb. Скачать 27.8 Kb.
|
|
В задачах в исходных данных: x – соответствует последней цифре зачетной книжки студента (число 8) y – соответствует предпоследней цифре зачетной книжки студента (число 2) Задача 1. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры tк = 43 °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина tн = 17°С. Модуль объемной упругости бензина Еж = 1300 МПа, коэффициент температурного расширения βt= 8*10-4 1/град. Решение Формула увеличения обьема жидкости при нагревании  Формула изменения обьема при сжатии 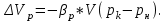 Так как коэффициент обьемного сжатия обратно пропорционален модулю упругости жидкости, имеем: 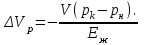 Так как канистра абсолютно жесткая, то изменение объема равно нулю: 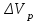 + +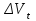 = 0 , т.е = 0 , т.е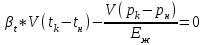  Задача 2. Определить объемный модуль упругости жидкости, если под действием груза А массой m = 266 кг поршень опустился на расстояние Δh = 5 мм. Начальная высота положения поршня (без груза) Н = 3,5 м, диаметр поршня d = 80 мм, а резервуара D =300 мм, высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким (Рис.1). Решение Согласно определению объемного модуля сжатия жидкости: 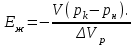 Объем резервуара, содержащего жидкость будет равен: 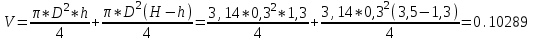 Задача 3. Воздух поступает в горизонтальную трубу с внутренним диаметром d = 152 мм под давлением p1 = (2,86+0,2x) МПа при температуре t = 220 °С со скоростью v1 = (58 +2y) м/с. Предполагая газ идеальным, а течение изотермическим, найти скорость и расстояние от входа до того сечения, где давление p2 = 1,07 МПа. Принять, что величина коэффициента гидравлического сопротивления постоянна и равна λ = 0,16. Задача 4. Найти распределение температуры и давления по длине газопровода при установившемся изотермическом в поперечном сечении 6 течении идеального газа (метана), если объемный расход газа приведенный к нормальным условиям Qат = (10 +x) млн м /сут, плотность ρат = 0,714 кг/м , температура газа при подаче в трубопровод Tн = (323 +y) K, давление pн = 5,4 МПа. Длина газопровода L = (220 +x) км, диаметр d = 720 мм. Температура грунта Tг = 275 K, коэффициент теплопередачи α = 1,5 Вт/м 2 ·град; коэффициент гидравлического сопротивления λ = 0,01. Газовая постоянная метана Rг = 519,625 Дж/кг·град, теплоемкость сp = 2,31 кДж/кг·град. Рис. 1 Задача 5. Определить режим течения и потери давления на трение при перекачке неньютоновской (степенной) жидкости со степенным реологическим законом τ = k(du/dr)n при величине меры консистенции жидкости k = (1,2+0,1x) Па·с 0,9 и степени нелинейности n = 0,9. Плотность жидкости ρ = 1200 кг/м 3 . Длина горизонтального трубопровода L = (1000+10y) м, внутренний диаметр трубопровода d = 0,5 м, средняя скорость перекачки u = 1м/с. Труба – гидравлически гладкая. Задача 6. Определить перепад давления при движении по трубопроводу длиной L = (1+0,2x) км диаметром d = (1 +0,1y) м вязкопластичной жидкости с начальным напряжением сдвига τ0 = 7,5 Па, пластической вязкостью μp = 0,95 Па*с и плотностью ρ = 1200 кг/м 3 , перекачиваемой со средней скоростью v = 2,83 м/с. Принять, что режим течения – турбулентный. Задача 7. Определить коэффициент проницаемости пористой среды (в Дарси), если известно, что коэффициент фильтрации с = (0,3+0,1x)*10-4 см/с, а кинематический коэффициент вязкости фильтрующейся жидкости ν = 10-6 м /с. Фильтрация жидкости происходит по закону Дарси. Задача 8. Определить коэффициенты проницаемости и фильтрации для цилиндрических горизонтальных образцов пористой среды диаметром d = (5+x) см, длиной ℓ= (20+y) см, если разность давлений на концах образца составляет p1–p2 = 300 мм рт. ст., расход жидкости Q = 1,70 л/ч, динамическая вязкость жидкости μ = 5 мПа*с, плотность ρ = 0,85 г/см 3 . Найти также скорость фильтрации. Задача 9. Определить по формуле Щелкачева, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q = (200+5y) м 3 /сут, мощность пласта h = 5 м, коэффициент пористости m = (16+x) %, коэффициент проницаемости k = 0,2 Д, плотность нефти ρ = 0,8 г/см 3 , динамическая вязкость μ = 5 мПа*с . Скважина гидродинамически совершенна, радиус её rc = 0, 1 м. Задача 10. Определить дебит дренажной галереи шириной В = 100 м, если мощность пласта h = (10+x) м, расстояние до контура питания ℓ = (10+y) км, коэффициент проницаемости пласта k = 1 Д, динамический коэффициент вязкости жидкости μ= 1 сП, давление на контуре питания pк = 9,8 МПа и давление в галерее pг = 7,35 МПа. Движение жидкости напорное, подчиняется закону Дарси. |
