Главная страница
Навигация по странице:

  • Экономический смысл дополнительных переменных

  • Итерация №0 .1. Проверка критерия оптимальности

  • 2. Определение новой базисной переменной

  • 3. Определение новой свободной переменной

  • 4. Пересчет симплекс-таблицы

  • Итерация №1 .1. Проверка критерия оптимальности

  • 1. Проверка критерия оптимальности

  • Анализ оптимального плана

    		•

    3 ЗАДАЧИ. Решение х 11 60Х 12 110 х 21 210Х 22 170 х 1 60170190420 х 2 110210190510


    Скачать 75.67 Kb.
    НазваниеРешение х 11 60Х 12 110 х 21 210Х 22 170 х 1 60170190420 х 2 110210190510
    Дата25.03.2023
    Размер75.67 Kb.
    Формат файлаdocx
    Имя файла3 ЗАДАЧИ.docx
    ТипРешение
    #1014051

    Задача 1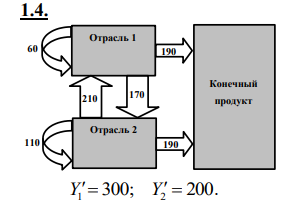



    Решение:

    Х11=60;Х12=110;

    Х21=210;Х22=170

    Х1=60+170+190=420

    Х2=110+210+190=510

     = 60/420=0,1429

     = 170/510=0,33

     = 210/420=0,5

     = 110/510=0,2157

    Х′1   0,14296Х′1+0,33Х′2 + 300

    Х′2   0,5Х′1+0,2157Х′2 + 200

    0,64296Х′1   0,33Х′2 + 300

    Х′1   0,51Х′2+466,59

    Х′2   0,6(0,51Х′2+466,59) + 0,2157′2+ 200

    Х′2=0,11Х′2+ 186,5+0,2157Х′2+200

    Х′2= 386,5:0,57

    Х′2= 678,1

    Х′1= 0,24*678,1+ 466,59

    Х′1= 629,31

    ЗАДАЧА 2
    Обозначим: А1 - число изготовленных стульев, А2 - число изготовленных столов.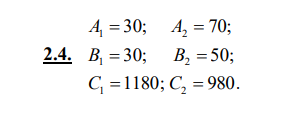
    :
    45 А1 + 80 А2 → maA ,

    30А1 + 70 А2 ≤ 1180 ,

    30 А1 + 50 А2 ≤ 980 ,

    А1 ≥ 0 ,
    А2 ≥ 0 .

    Изобразим на координатной плоскости область, соответствующую ограничениям модели. Каждая точка этой области будет соответствовать определенному выпуску

     

     
     


    Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
    Определим максимальное значение целевой функции F(A) = 45A1+80A2 при следующих условиях-ограничений.
    30A1+70A2≤1180
    30A1+50A2≤980
    Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
    В 1-м неравенстве смысла (≤) вводим базисную переменную A3. В 2-м неравенстве смысла (≤) вводим базисную переменную A4. В 3-м неравенстве смысла (≥) вводим базисную переменную A5 со знаком минус.
    30A1+70A2+A3 = 1180
    30A1+50A2+A4 = 980
    -A5 = 0
    Расширенная матрица системы ограничений-равенств данной задачи:

    30
    70
    1
    0
    0
    1180

    30
    50
    0
    1
    0
    980

    0
    0
    0
    0
    -1
    0














    Приведем систему к единичной матрице методом жордановских преобразований.
    1. В качестве базовой переменной можно выбрать A3.
    2. В качестве базовой переменной можно выбрать A4.
    3. В качестве базовой переменной можно выбрать A5.
    Получаем новую матрицу:

    30
    70
    1
    0
    0
    1180

    30
    50
    0
    1
    0
    980

    0
    0
    0
    0
    1
    0


    Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем A = (3,4,5).
    Выразим базисные переменные через остальные:
    A3 = -30A1-70A2+1180
    A4 = -30A1-50A2+980
    A5 = 0
    Подставим их в целевую функцию:
    F(A) = 45A1+80A2
    30A1+70A2+A3=1180
    30A1+50A2+A4=980
    A5=0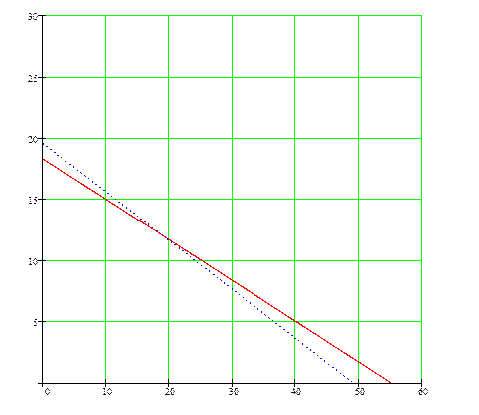


    Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

    A =

    30
    70
    1
    0
    0

    30
    50
    0
    1
    0

    0
    0
    0
    0
    1














    Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
    Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
    Решим систему уравнений относительно базисных переменных: A3, A4, A5
    Полагая, что свободные переменные равны 0, получим первый опорный план:
    A0 = (0,0,1180,980,0)
    Базисное решение называется допустимым, если оно неотрицательно.

    Базис
    B
    A1
    A2
    A3
    A4
    A5

    A3
    1180
    30
    70
    1
    0
    0

    A4
    980
    30
    50
    0
    1
    0

    A5
    0
    0
    0
    0
    0
    1

    F(A0)
    0
    -45
    -80
    0
    0
    0


    Переходим к основному алгоритму симплекс-метода.
    Итерация №0.
    1. Проверка критерия оптимальности.
    Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
    2. Определение новой базисной переменной.
    В качестве ведущего выберем столбец, соответствующий переменной A2, так как это наибольший коэффициент по модулю.
    3. Определение новой свободной переменной.
    Вычислим значения Di по строкам как частное от деления: bi / ai2
    и из них выберем наименьшее:
    min (1180 : 70 , 980 : 50 , - ) = 166/7
    Следовательно, 1-ая строка является ведущей.
    Разрешающий элемент равен (70) и находится на пересечении ведущего столбца и ведущей строки.

    Базис
    B
    A1
    A2
    A3
    A4
    A5
    min

    A3
    1180
    30
    70
    1
    0
    0
    118/7

    A4
    980
    30
    50
    0
    1
    0
    98/5

    A5
    0
    0
    0
    0
    0
    1
    -

    F(A1)
    0
    -45
    -80
    0
    0
    0
    0


    4. Пересчет симплекс-таблицы.
    Формируем следующую часть симплексной таблицы. Вместо переменной A3 в план 1 войдет переменная A2.
    Строка, соответствующая переменной A2 в плане 1, получена в результате деления всех элементов строки A3 плана 0 на разрешающий элемент РЭ=70. На месте разрешающего элемента получаем 1. В остальных клетках столбца A2 записываем нули.
    Таким образом, в новом плане 1 заполнены строка A2 и столбец A2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
    Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
    НЭ = СЭ - (А*В)/РЭ
    СТЭ - элемент старого плана, РЭ - разрешающий элемент (70), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
    Представим расчет каждого элемента в виде таблицы:

    B
    A1
    A2
    A3
    A4
    A5

    1180 : 70
    30 : 70
    70 : 70
    1 : 70
    0 : 70
    0 : 70

    980-(1180*50):70
    30-(30*50):70
    50-(70*50):70
    0-(1*50):70
    1-(0*50):70
    0-(0*50):70

    0-(1180*0):70
    0-(30*0):70
    0-(70*0):70
    0-(1*0):70
    0-(0*0):70
    1-(0*0):70

    0-(1180*-80):70
    -45-(30*-80):70
    -80-(70*-80):70
    0-(1*-80):70
    0-(0*-80):70
    0-(0*-80):70



    Получаем новую симплекс-таблицу:

    Базис
    B
    A1
    A2
    A3
    A4
    A5

    A2
    118/7
    3/7
    1
    1/70
    0
    0

    A4
    960/7
    60/7
    0
    -5/7
    1
    0

    A5
    0
    0
    0
    0
    0
    1

    F(A1)
    9440/7
    -75/7
    0
    8/7
    0
    0


    Итерация №1.
    1. Проверка критерия оптимальности.
    Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
    2. Определение новой базисной переменной.
    В качестве ведущего выберем столбец, соответствующий переменной A1, так как это наибольший коэффициент по модулю.
    3. Определение новой свободной переменной.
    Вычислим значения Di по строкам как частное от деления: bi / ai1
    и из них выберем наименьшее:
    min (166/7 : 3/7 , 1371/7 : 84/7 , - ) = 16
    Следовательно, 2-ая строка является ведущей.
    Разрешающий элемент равен (84/7) и находится на пересечении ведущего столбца и ведущей строки.

    Базис
    B
    A1
    A2
    A3
    A4
    A5
    min

    A2
    118/7
    3/7
    1
    1/70
    0
    0
    118/3

    A4
    960/7
    60/7
    0
    -5/7
    1
    0
    16

    A5
    0
    0
    0
    0
    0
    1
    -

    F(A2)
    9440/7
    -75/7
    0
    8/7
    0
    0
    0


    4. Пересчет симплекс-таблицы.
    Формируем следующую часть симплексной таблицы. Вместо переменной A4 в план 2 войдет переменная A1.
    Строка, соответствующая переменной A1 в плане 2, получена в результате деления всех элементов строки A4 плана 1 на разрешающий элемент РЭ=84/7. На месте разрешающего элемента получаем 1. В остальных клетках столбца A1 записываем нули.
    Таким образом, в новом плане 2 заполнены строка A1 и столбец A1. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
    Представим расчет каждого элемента в виде таблицы:

    B
    A1
    A2
    A3
    A4
    A5

    166/7-(1371/7*3/7):84/7
    3/7-(84/7*3/7):84/7
    1-(0*3/7):84/7
    1/70-(-5/7*3/7):84/7
    0-(1*3/7):84/7
    0-(0*3/7):84/7

    1371/7 : 84/7
    84/7 : 84/7
    0 : 84/7
    -5/7 : 84/7
    1 : 84/7
    0 : 84/7

    0-(1371/7*0):84/7
    0-(84/7*0):84/7
    0-(0*0):84/7
    0-(-5/7*0):84/7
    0-(1*0):84/7
    1-(0*0):84/7

    13484/7-(1371/7*-105/7):84/7
    -105/7-(84/7*-105/7):84/7
    0-(0*-105/7):84/7
    11/7-(-5/7*-105/7):84/7
    0-(1*-105/7):84/7
    0-(0*-105/7):84/7



    Получаем новую симплекс-таблицу:

    Базис
    B
    A1
    A2
    A3
    A4
    A5

    A2
    10
    0
    1
    1/20
    -1/20
    0

    A1
    16
    1
    0
    -1/12
    7/60
    0

    A5
    0
    0
    0
    0
    0
    1

    F(A2)
    1520
    0
    0
    1/4
    5/4
    0


    1. Проверка критерия оптимальности.
    Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
    Окончательный вариант симплекс-таблицы:

    Базис
    B
    A1
    A2
    A3
    A4
    A5

    A2
    10
    0
    1
    1/20
    -1/20
    0

    A1
    16
    1
    0
    -1/12
    7/60
    0

    A5
    0
    0
    0
    0
    0
    1

    F(A3)
    1520
    0
    0
    1/4
    5/4
    0


    Оптимальный план можно записать так:
    A1 = 16, A2 = 10
    F(A) = 45*16 + 80*10 = 1520
    Анализ оптимального плана.
    Значение 0 в столбце A1 означает, что использование A1 - выгодно.
    Значение 0 в столбце A2 означает, что использование A2 - выгодно.
    Значение 1/4 в столбце A3 означает, что теневая цена (двойственная оценка) равна y1=1/4.
    Значение 11/4 в столбце A4 означает, что теневая цена (двойственная оценка) равна y2=11/4.
    Значение 0 в столбце A5 означает, что теневая цена (двойственная оценка) равна y3=0.
    Задание 3.

    Задана матрица вероятностей перехода дискретной цепи Маркова из i-го состояния в j-ое за один шаг 𝑃 и распределение вероятностей по состояниям в начальный момент времени 𝑝1(0); 𝑝2(0); 𝑝3(0). Найти:

    1. распределение вероятностей по состояниям в момент t=1;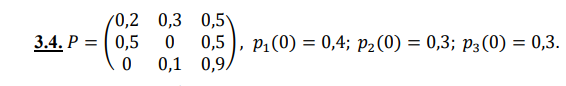


    Решение:

    1. распределение вероятностей по состояниям в момент t=1;

    Р1(1) = 0,4*0,2 + 0.3*0,5 + 0,3*0 = 0,23

    Р2(1) = 0,4*0,3 + 0,3*0 + 0,3*0,1 = 0,15

    Р3(1) = 0,4*0,5 + 0,3*0,5 + 0,3*0.9 = 0,62

    2. стационарное распределение.

     Р1 = Р1*Р11 + Р2*Р21 + Р3*Р31

    Р2 = Р1*Р12 + Р2*Р22 + Р3*Р32

    Р1 + Р2 + Р3 = 1

     Р1 = 0,2Р1 + 0,52Р2

    Р2 = 0,3Р1 + 0,1Р3

    Р1 + Р2 + Р3 = 1

     0,9Р1 = 0,2Р2

    Р2 = 0,5Р1 + 0,8Р3

    Р1 + Р2 + Р3 = 1

     Р2 = 0,9/0,52Р1 = 4,5Р1

    4,5Р1 = 0,5Р1 + 0,1Р3

    Р1 + Р2 + Р3 = 1

     Р2= 4,5Р1

    4Р1 = 0,1Р3

    Р1 + Р2 + Р3 = 1

     Р2= 4,5Р1

    Р3= 4/0,1Р1 = 5Р1

    Р1 + 4,5Р1+ 5Р1= 1

     Р2= 4,5Р1

    Р3= 4/0,1Р1 = 5Р1

    10,5Р1 = 1

     Р2= 4,5*0,095 » 0,43

    Р3= 4/0,8Р1= 5*0,095 » 0,48

    Р1 = 1/10,5 » 0,095

    Получили: Р1 = 0,095; Р2= 0,43; Р3= 0,48

    Список литературы

    1. Акулич М.В. Оценка стоимости бизнеса. - СПб, Питер, 2018. - 272 с.

    2. Валдайцев С.В. Оценка бизнеса: учебник. - М.: ТК ВЕЛБИ, 2017. - 352 с.

    3. Егерев В.А. Стоимость бизнеса - М.: Дело, 2019. - 480 с.

    4. Ленская С.А., Грязнова А.Г., Федотова М.А. Оценка бизнеса: учебник. - Финансы и статистика, 2016. - 295 с.

    5. Сычева Г.И. Оценка стоимости предприятия (бизнеса). - М.: Высшее образование, 2018. - 384 с.

    6. Фельдман А.Б. Оценка дебиторской и кредиторской задолженности. - М.: РИО МАОК, 2016. - 52 с.

    7. Финансовый менеджмент: Учебное пособие / Под ред. проф. Е.И. Шохина. - М.: ИД ФБК - ПРЕСС, 2019. - 408с.

    8. Финансовый анализ: учебное пособие/ Э.А. Маркарьян, Г.П. Герасименко, С.Э. Маркарьян. - 6-е изд., перераб. - М.: КНОРУС, 2020. - 224 с.

    9. Финансовый менеджмент: теория и практика: Учеб. / Под ред. Е.С. Стояновой. - 6-е изд. - М.: Издательство «Перспектива»; 2017. - 656 с.

    10. Черняк В.З. Оценка бизнеса. - М., Финансы и статистика, 2016. - 271 с.

    11. Янковский К.П. Способы и методы оценки бизнеса. - СПб., Питер, 2017. - 150 с.

    написать администратору сайта