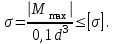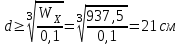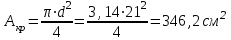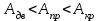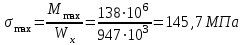|
|
2783192 механика. Решение Левая опора точка
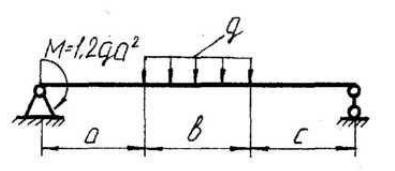
Задача 1 - на равновесие тела под действием произвольной плоской системы сил. При ее решении следует учесть, что распределенная нагрузка, действующая на балку, должна быть заменена соответствующей ей сосредоточенной силой.
План решения задачи
1) Вычертить схему нагружения балки.
2) Определить реакции опор.
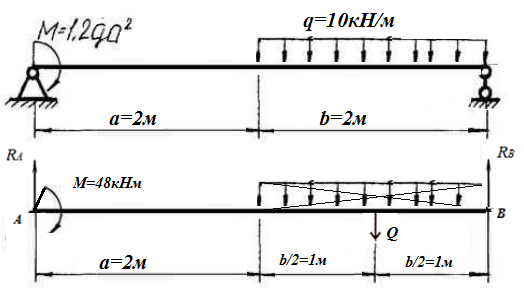
Дано: q=10 кН/м, а=2 м, b=2 м, с = 0 м, М=1,2qa2=1,2·10·22=48 кН·м
Решение
Левая опора (точка А) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.
Правая опора (точка В) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.
Заменяем распределенную нагрузку сосредоточенной:
Q=q·b; Q=10 · 2=20кН
Составляем уравнения моментов относительно точек крепления:
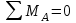 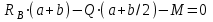
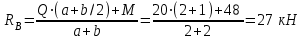
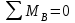 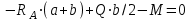
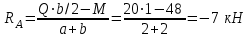
Проверка: 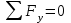 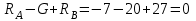
Реакция опоры А противоположна выбранной.
Задача 2 Расчет на прочность ступенчатого бруса круглого сечения на осевое растяжение – сжатие
План решения задачи
1. Вычертить схему нагружения бруса.
2. Построить эпюру продольных сил.
3. Определить из условия прочности диаметры на всех участках бруса. Округлить полученные значения до стандартных размеров по ГОСТ 6636- 69. Дать эскиз ступенчатого бруса с указанием диаметров на каждом участке (материал бруса-Ст.3), [Ϭ]=160 МПа.
4. Построить эпюру напряжений.
5. Определить абсолютную деформаций по его длине (длина бруса l=2м.).
Дано: F1=5кН, F2=30кН, F3=50кН, a=0,2м, b=0,5м
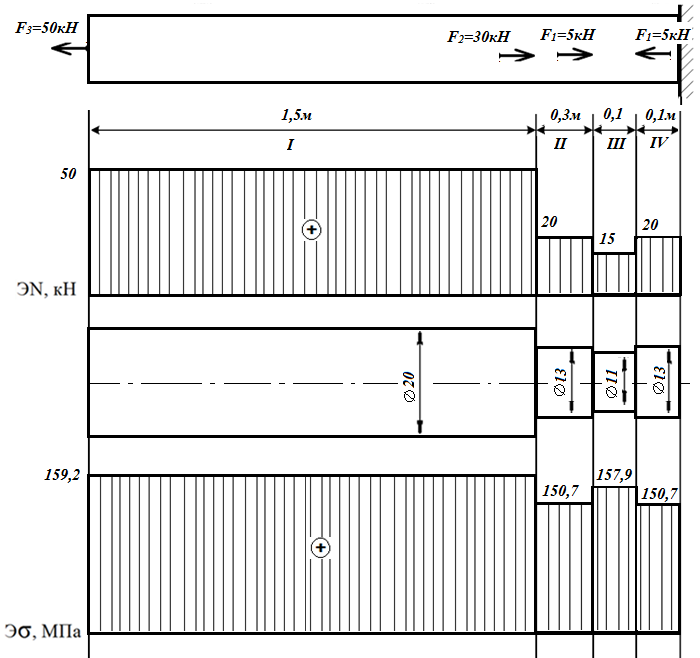
Решение
Разделим брус на участки, границы которых определяются местами изменения поперечных размеров бруса или точками приложения внешних нагрузок.
Рассматриваемый брус имеет три участка.
Применяем метод сечений. Определяем продольную силу N, выражая ее через внешние силы.
На участке I продольная сила равна:
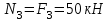
На участке II продольная сила равна:
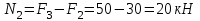
На участке III продольная сила равна:
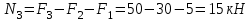
На участке IV продольная сила равна:
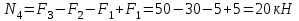
Строим эпюру продольных сил N.
Из расчета на прочность при растяжении-сжатии определим для каждого участка конструкции необходимую площадь круглого поперечного сечения и запроектируем сечение заданной формы.
Требуемая площадь сечения для первого участка:
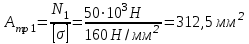
Площадь круга 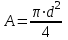 ,тогда ,тогда
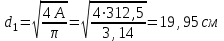 , принимаем , принимаем 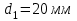
Требуемая площадь для второго участка
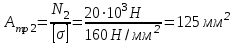
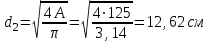 , принимаем , принимаем 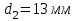
Требуемая площадь для третьего участка:
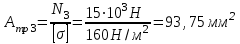
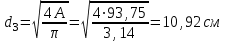 , принимаем , принимаем 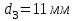
Требуемая площадь для четвертого участка:
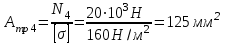
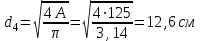 , принимаем , принимаем 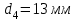
Построим в выбранном масштабе эскиз опоры:
Пересчитаем фактическую площадь на участках:
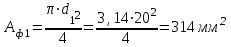
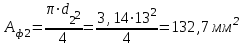

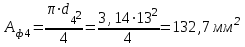
Определим нормальные напряжения на участках.
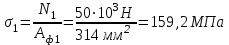
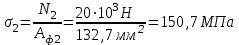
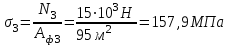
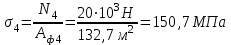
Условие прочности выполняется по всей длине.
Полное удлинение бруса равно алгебраической сумме удлинений его участков
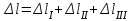
Определим их, используя формулу Гука
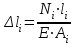
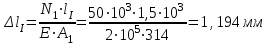
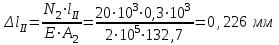
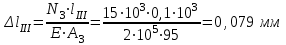
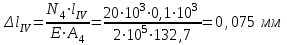
Абсолютная деформация стержня
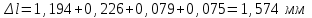
Задача 3 Расчет валов на кручение
План решения задачи
1) Вычертить схему вала.
2) Определить из условия равновесия вала мощность Р0, пренебрегая трением в подшипниках.
3) Определить скручивающие моменты, передаваемые каждым шкивом.
4) Построить эпюру крутящих моментов.
5) Определить диаметр вала на каждом участке из условия прочности; округлить полученные величины до стандартных размеров в большую сторону по ГОСТ 6636-69. Дать эскиз ступенчатого вала с указанием диаметров. (Материал вала-Ст.45.)
6) Определить величину yгла закручивания для всего вала, принимая за неподвижное сечение один из концов вала (а=1м).
7. Построить эпюру углов закручивания, (а=1м). Диаметры валов согласно ГОСТ 663669 должны соответствовать ряду предпочтительных чисел: 5,0; 6,0; 7,5; 8,0; 8,5; 9,0; 9,5; 10; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50.
Дано: P1=0,1кВт, P2=0,2кВт, P3=0,3кВт, P4=0,4кВт, = 4 с-1
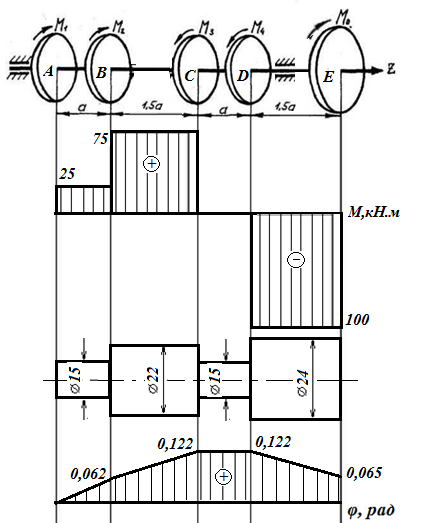
Решение:
Определяем величины скручивающих моментов М1 , М2 и М3
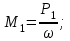 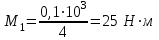
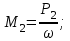 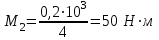
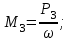 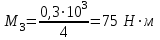
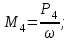 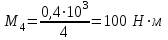
Определяем уравновешивающий момент М 4 SМz = 0; – М 1 – М 2 + М 3 + M4– М0 =0; М 0 = – М 1 – М 2 + М 3 + M4 = – 25 – 50 +75+100= 100 Н·м.
Определим методом сечений значения крутящих моментов, действующих на участках вала между шкивами.
Участок I
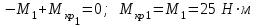
Участок II
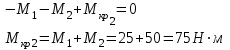
Участок III

Участок IV
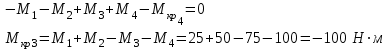
По полученным значениям строим эпюру крутящих моментов.
Определим размеры поперечного сечения бруса для каждого участка в отдельности.
Для этого используем условие прочности при кручении
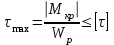
Определяем диаметр вала на каждом участке, учитывая, что полярный момент сопротивления равен, м3:
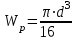
В итоге получаем следующую зависимость
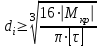
Подставляя числовые значения, получим
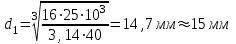
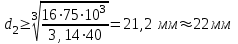
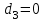
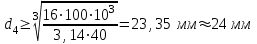
Определяем углы закручивания сечений вала, приняв условно неподвижным крайнее левое сечение А вала.
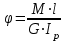
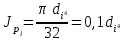 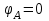
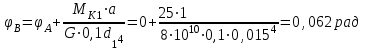
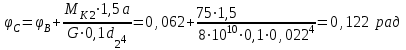
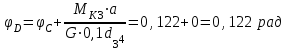
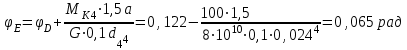
Задача 4. Расчет на прочность балок при изгибе
План решения задачи
1) Вычертить схему нагружения балки (принять l=6м).
2) Построить эпюры поперечной силы Q и изгибающего момента Мизг.
3) Подобрать круглое сечение, прямоугольное сечение (с отношением высоты к ширине, равное 2) и двутавровое сечение (материал балки - Ст.3).
4) Сравнить вес одного погонного метра длины каждого профиля.
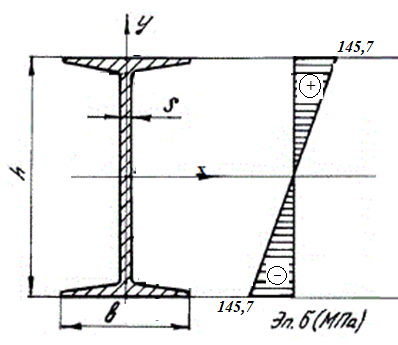
5) Построить эпюру нормальных напряжений в опасном сечении двутавровой балки.
Дано: q=30кН/м, F=15кН, М=12 кНм, n=1/3, k=1/6
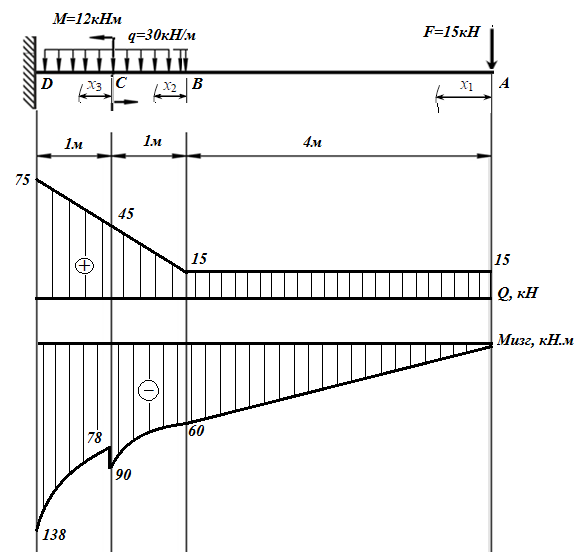
Решение:
Построение эпюр изгибающих моментов и поперечных сил. Балка имеет три участка. Проводим на каждом участке сечение на расстоянии x от начала участка. Из условия равновесия отсеченной части определяем поперечные силы и изгибающие моменты. По полученным значениям строим эпюру поперечных сил y Q и эпюру изгибающих моментов.
Участок АВ 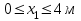
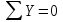 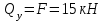
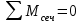 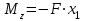
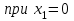 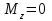
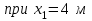 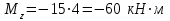
Участок ВC 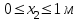
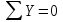 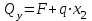
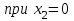 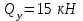
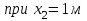 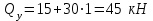
 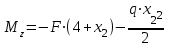
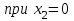 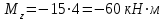
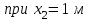 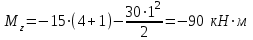
Участок CD 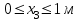
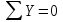 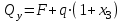
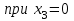 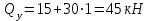
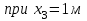 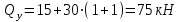
 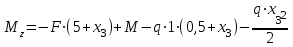
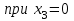 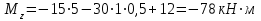
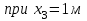 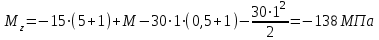
Подбор размеров поперечного сечения производится из условия прочности по нормальным напряжениям. По построенной эпюре Mzопределим максимальный расчетный изгибающий момент Mzmax=138кН·м
Из условия прочности при поперечном изгибе для симметричных сечений:
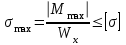
находим требуемый осевой момент сопротивления (𝑊𝑥треб):
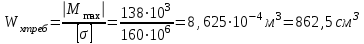
a) двутавровое сечение:
По сортаменту прокатной продукции подбираем сечение с наиболее подходящим к 𝑊𝑥треб осевым моментом сопротивления.
Выбираем двутавр № 40 с 𝑊𝑥=953 см3
Площадь сечения двутавра № 40: Адвутавра=72,6 см2
б) прямоугольное сечение , h/b=2
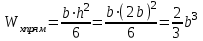
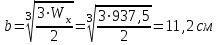
Принимаем b=11,2 см, h=22,4 см
Площадь прямоугольного сечения: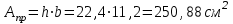
в) круглое сечение
Так как для круга
 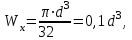 то то
 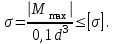
Отсюда находим диаметр сечения:
 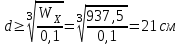
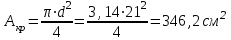
Вес балки на единицу длины пропорционален площади её сечения.
Все сечения подбирались для одной и той же схемы и материала, поэтому вес балки в данном случае зависит только от площади ее поперечного сечения.
Сечение с меньшей площадью и будет наиболее экономичным.
Сравнение площадей
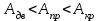
показывает, что наиболее экономичным является двутавровое сечение.
Вычисляем нормальные напряжения в опасном сечении двутавровой балки
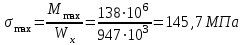
Задача 5 Расчет вала на изгиб с кручением
План решения задачи
1. Определить мощность на шкиве, где она не задана.
2. Определить моменты, передаваемые каждым шкивом.
3. Построить эпюру крутящих моментов.
4. Определить давление, передаваемое шкивами на вал, считая, что натяжение ведущего ремня в два раза больше, чем натяжение ведомого.
5. Показать на схеме в аксонометрии расположение усилий, действующих на вал и разложив их по осям, определить вертикальные и горизонтальные составляющие.
6. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях и эпюру суммарного изгибающего момента.
7. Определить диаметр вала, пользуясь четвертой теорией прочности, если [Ϭ]=110 МПа; а=0,2 м. Диаметры шкивов соответственно равны: D1=180 мм; D2=160 мм; D3=140 мм; D4=200 мм.
Мощности, передаваемые шкивами, кВт
|
, с-1
|
1 град
|
2 град
|
3 град
|
P1
|
P2
|
P3
|
P4
|
|
10
|
20
|
10
|
100
|
0
|
270
|
60
|
Решение:
Мощность на шкиве 1 не задана, определим ее из условия равновесия
ΣРi= Р1 - Р2 -Р3-Р4= 0,
Р1 = Р2 +Р3+Р4=10+20+10=40 кВт
Определение внешних моментов, действующих на вал
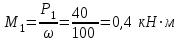
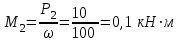
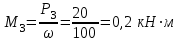
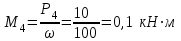
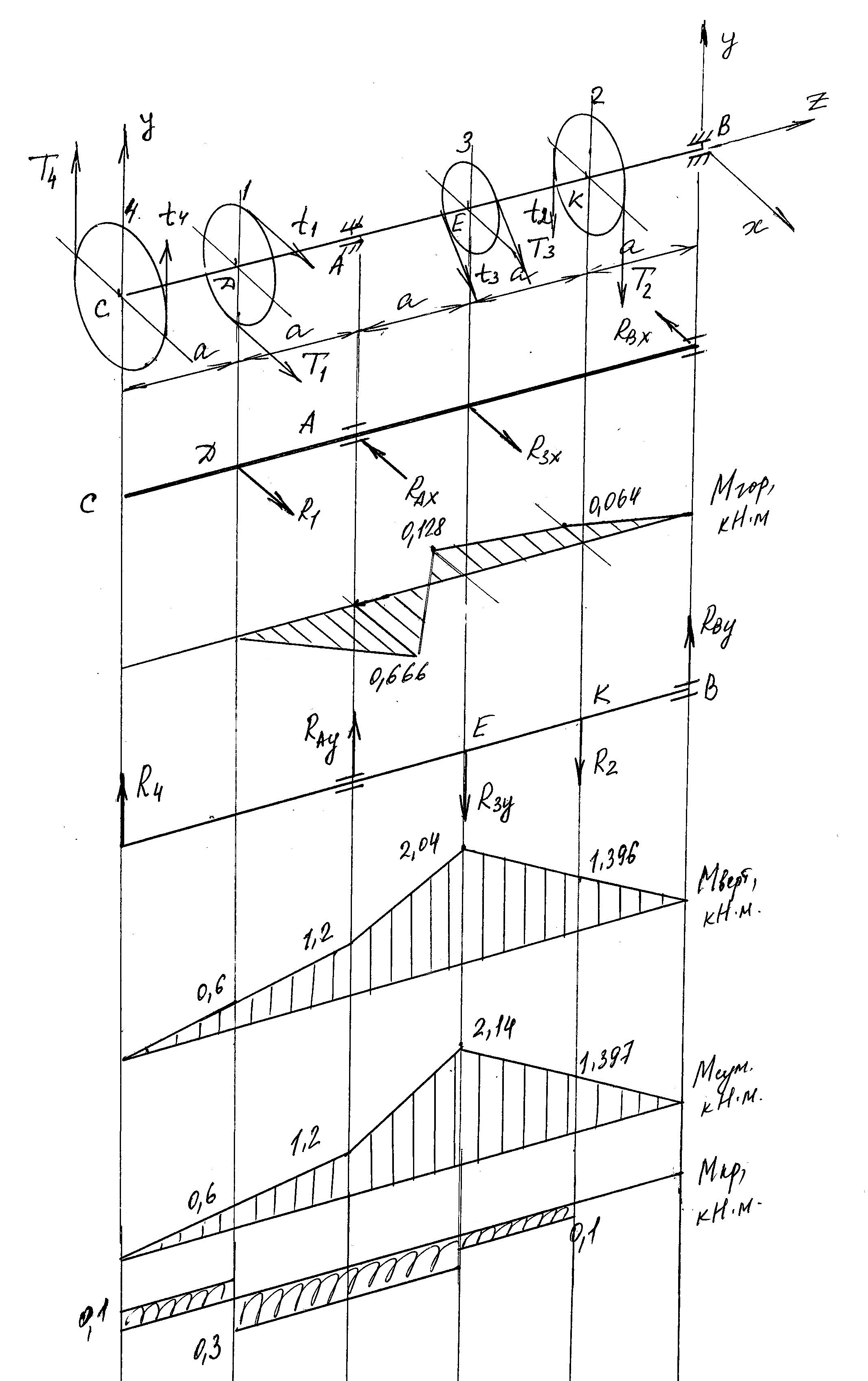
Построение эпюры крутящего момента MКР
Участок СD
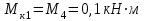
Участок DE
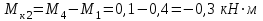
Участок EK
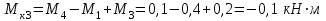
Участок KB
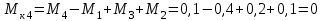
Определение внешних изгибающих нагрузок
Определяем окружные усилия
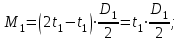 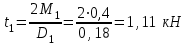
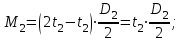 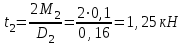
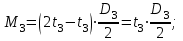 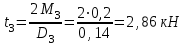
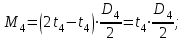 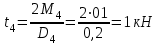
Определи давления на вал
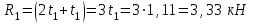
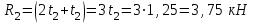
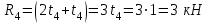
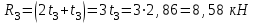
Так как действие силы R3не совпадает с направлением выбранных осей, то её заменяем на проекции
R3x = R3cos60° = 8,58cos60°= 4,29 кН,
R3Y= R3 sin60°=8,58sin60°= 7,43 кН.
Определим опорные реакции и построим эпюру изгибающих моментов в горизонтальной плоскости.
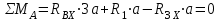
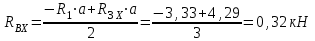
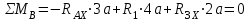
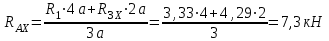
Проверка: 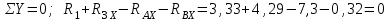
Изгибающие моменты
В сечении C: 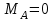
В сечении D: 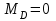
В сечении А: 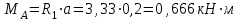
В сечении Е: 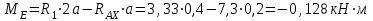
В сечении В: 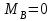
В сечении К: 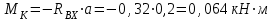
Определим опорные реакции и построим эпюру изгибающих моментов в вертикальной плоскости.
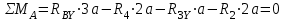
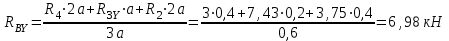
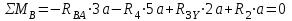
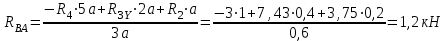
Проверка: 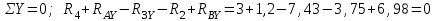
Изгибающие моменты
В сечении C: 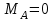
В сечении D: 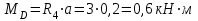
В сечении А: 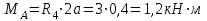
В сечении Е: 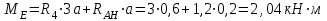
В сечении В: 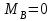
В сечении К: 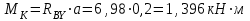
Строим эпюру суммарного изгибающего момента.
В сечении С: 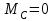
В сечении D: 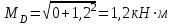
В сечении A: 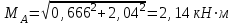
В сечении K: 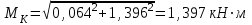
В сечении B: 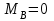
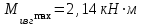
Определение диаметра вала
Рассматриваемый вал испытывает деформацию «изгиб с кручением», используем IVтеорию прочности. Для круглого вала изгиб с кручением можно заменить эквивалентным изгибом с моментом
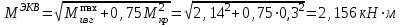
Так как изгиб с кручением заменяется эквивалентным моментом, то следует использовать условие прочности при изгибе
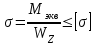
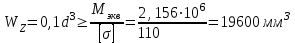
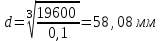
Округляем до стандартного размера и принимаем диаметр вала d =60 мм.
Литература
1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. – М.: «Высшая школа», 2000.
2. Сборник задач по сопротивлению материалов / под ред. В.К. Качурина. – М.: «Наука», 1972.
3. Ицкович Г.М., Минин Л.С., Винокуров А.И. Руководство к решению задач по сопротивлению материалов. – М.: «Высшая школа», 2001.
4. Саргсян А.Е. Сопротивление материалов, теории упругости и пластичности. Основы теории с примерами расчетов.- М.: «Высшая Школа», 2000 |
|
|
 Скачать 1.01 Mb.
Скачать 1.01 Mb.
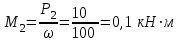
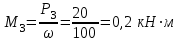
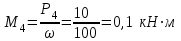

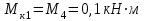
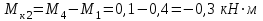
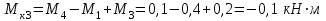
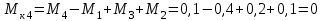
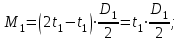
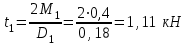
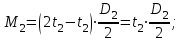
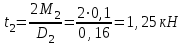
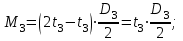
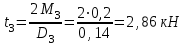
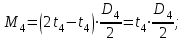
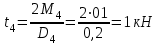
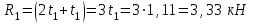
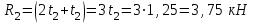
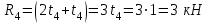
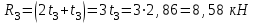
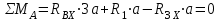
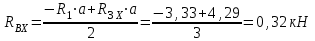
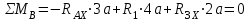
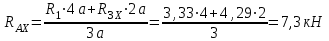
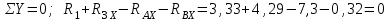
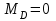
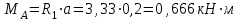
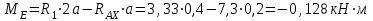
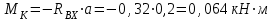
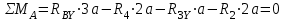
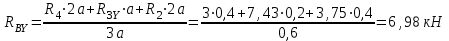
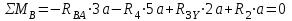
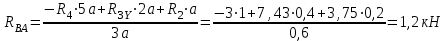
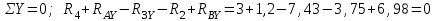
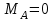
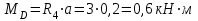
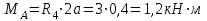
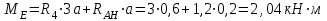
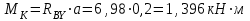
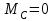
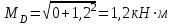
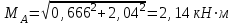
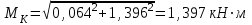
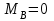
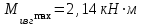
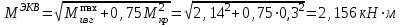
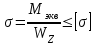
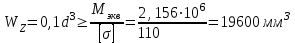
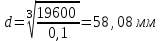



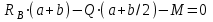
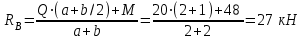
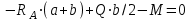
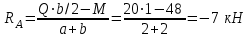
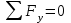
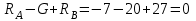

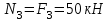
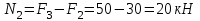
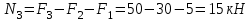
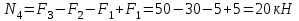
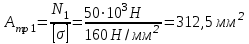
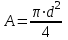 ,тогда
,тогда 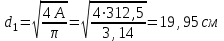 , принимаем
, принимаем 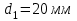
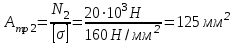
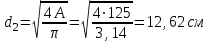 , принимаем
, принимаем 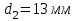
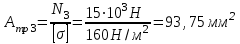
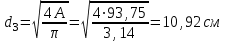 , принимаем
, принимаем 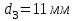
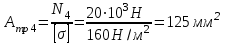
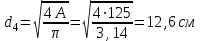 , принимаем
, принимаем 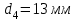
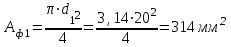
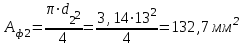

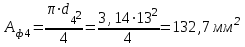
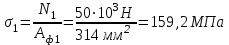
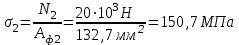
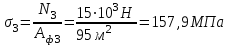
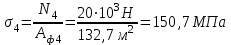
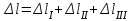
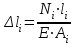
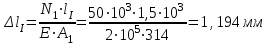
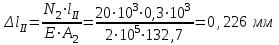
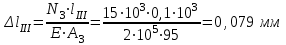
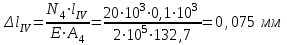
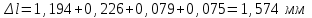

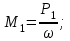
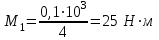
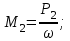
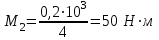
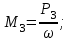
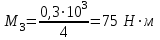
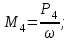
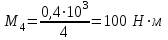
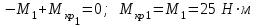
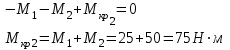

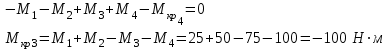
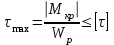
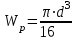
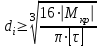
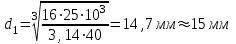
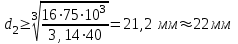
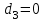
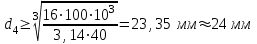
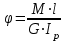
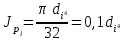
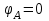
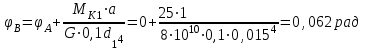
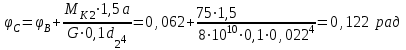
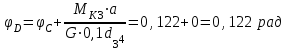
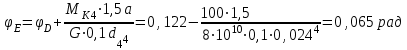

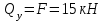
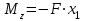
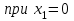
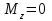
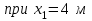
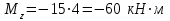
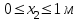
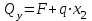
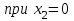
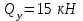
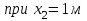
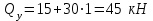
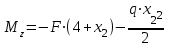
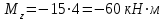
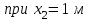
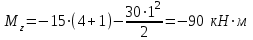
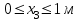
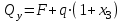
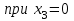
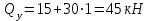
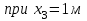
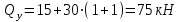
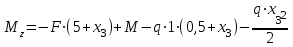
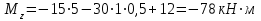
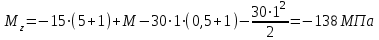
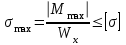
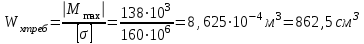
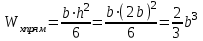
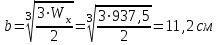
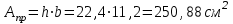

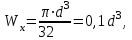 то
то