микроэкономика. Решение Линейная функция спроса имеет вид 1)
 Скачать 261.2 Kb. Скачать 261.2 Kb.
|
|
Тема 3. Поведение производителя и конкуренция Выбор варианта практического задания 4 осуществляется по первой букве фамилии студента (таблица 4.1). Таблица 4.1 Выбор варианта практического задания 4
Задачи Технологическая норма замещения факторов 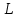 и и 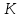 равна равна 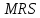 . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора 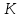 на на 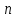 единиц. Сколько дополнительных единиц фактора единиц. Сколько дополнительных единиц фактора 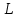 потребуется фирме? потребуется фирме?Значения показателей 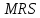 и и 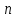 выбираются из таблицы 4.2 согласно варианту. выбираются из таблицы 4.2 согласно варианту.Таблица 4.2 Значения показателей 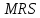 и и 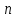 по вариантам по вариантам
Бланк выполнения практического задания 4 Технологическая норма замещения факторов 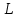 и и 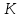 равна равна 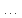 -2. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора -2. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора 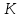 на на 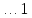 единиц. Сколько дополнительных единиц фактора единиц. Сколько дополнительных единиц фактора 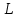 потребуется фирме? потребуется фирме?Решение Условие оптимального использования ресурсов: … Оптимум достигается тогда, когда предельная норма технического замещения факторов производства равна отношению цен на эти факторы производств. Графическое решение представлено на рисунке 4. ……… В силу отрицательного наклона изокванты данное отношение всегда является величиной отрицательной. Иногда для удобства вводят минус перед правой частью, но в большинстве случаев имеет значение абсолютная величина коэффициента. 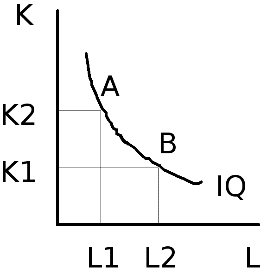 Рис.4. Предельная норма технологического замещения Как видно на рисунке 4, при переходе из точки А в точку В объем производства остается неизменным. Это означает, что сокращение выпуска в результате уменьшения затрат капитала ( К=К2-К1) компенсируется увеличением выпуска за счет использования дополнительного количества труда ( L=L2-L1). Вывод: в результате проведенных расчетов … мы получили, что нужно увеличить выпуск фактора L на единицу. Практическое задание 5 Тема 4. Рыночные структуры и стратегия поведения Задачи 1. Предположим, что на рынке действуют две фирмы, функции общих издержек 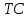 заданы уравнениями: заданы уравнениями: 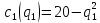 и и 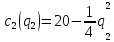 . Рыночный спрос описывается функцией: . Рыночный спрос описывается функцией: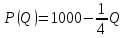 , ,где 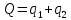 . . Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если: - фирмы конкурируют по Курно; - фирмы конкурируют по Бертрану; - фирмы конкурируют по сценарию Штакельберга. Изобразите решение на графике. 3. График предельных издержек фирмы-монополиста задан условием 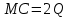 . Функция предельного дохода принимает вид: . Функция предельного дохода принимает вид: 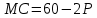 . Определите эластичность рыночного спроса . Определите эластичность рыночного спроса 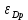 при оптимальном выпуске фирмы-монополиста. при оптимальном выпуске фирмы-монополиста.Рекомендации по выполнению практического задания 5 Изучив материалы по теме «Рыночные структуры и стратегия поведения», выполните расчеты в бланке выполнения практического задания 5 и покажите графическое решение. Бланк выполнения практического задания 5 Задачи 1. Предположим, что на рынке действуют две фирмы, функции общих издержек 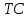 заданы уравнениями: заданы уравнениями: 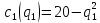 и и 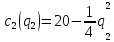 . Рыночный спрос описывается функцией: . Рыночный спрос описывается функцией: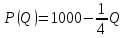 , ,где 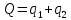 . .Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если: - фирмы конкурируют по Курно; - фирмы конкурируют по Бертрану; - фирмы конкурируют по сценарию Штакельберга. Изобразите решение на графике. Решение Стратегия по Курно предполагает, что … . Олигополия Курно — экономическая модель рыночной конкуренции. Названа в честь сформулировавшего её французского экономиста А.Курно (1801-1877). Основные положения модели: На рынке действует фиксированное число {\displaystyle N>1}  фирм, выпускающих экономическое благо одного наименования; фирм, выпускающих экономическое благо одного наименования;Вход на рынок новых фирм и выход из него отсутствуют; Фирмы обладают рыночной властью. Замечание: сам Курно не знал, что такое рыночная власть. Этот термин появился позднее; Фирмы максимизируют свою прибыль и действуют без кооперации. Общее количество фирм на рынке {\displaystyle N}  предполагается известным всем участникам. Каждая фирма, принимая своё решение, считает выпуск остальных фирм заданным параметром (константой). Функции издержек фирм {\displaystyle c_{i}(q_{i})} предполагается известным всем участникам. Каждая фирма, принимая своё решение, считает выпуск остальных фирм заданным параметром (константой). Функции издержек фирм {\displaystyle c_{i}(q_{i})} могут быть различны и также предполагаются известными всем участникам. могут быть различны и также предполагаются известными всем участникам.Функция спроса представляет собой убывающую функцию от цены блага. Цена блага задана как цена равновесия отраслевого рынка (величина отраслевого предложения равна величине спроса на данное экономическое благо при одной и той же цене). Решение задачи по Курно: … . В модели дуополии Курно предполагается, что в отрасли существуют только две фирмы, причем они идентичны. Тогда отраслевой объем производства равен сумме объемов производства фирмы 1 и фирмы 2: Составим далее уравнения совокупной и предельной выручки для каждой фирмы в отдельности. 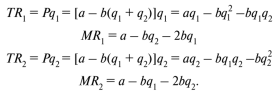 Допустим в целях упрощения, что общие, а следовательно, и предельные издержки равны нулю. Тогда в точке равновесия MR = МС = О, или Данный вид уравнения MR позволяет определить объем производства каждой из фирм через объем производства фирмы-соперницы: Другими словами, q2 является функцией реакции фирмы 2 на поведение фирмы 1, т.е. q2 =/2(tf,), а есть функция реакции фирмы 1 на поведение фирмы 2, или q{ =/1(<72). Рисунок 12.6 дает графическую интерпретацию кривых реакции фирмы 1 и фирмы 2. 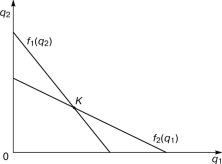 Графическое решение представлено на рисунке 5.1. Каждая фирмы производит весь отраслевой объем продукции, если конкурент сокращает свое производство до нуля. По мере нарастания объема выпуска конкурента другая фирма принимает этот факт за данность и сокращает свой объем производства. Поскольку по допущению фирмы идентичны, в точке пересечения двух кривых реагирования рынок делится поровну и qx = qr Данная точка представляет собой равновесие Курно. Обозначив объем производства отдельной фирмы в точке равновесия через q* и приравняв q{ и/2(^j), получим равновесный объем производства первой фирмы: или 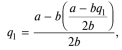 или или или Аналогично В этом случае равновесный объем предложения отрасли равен Если отказаться от допущения о нулевых издержках и обозначить величину неизменных предельных издержек фирмы в расчете на единицу изделия (что будет равнозначно средним переменным издержкам) через «с», тогда можно записать уравнение совокупной прибыли фирмы следующим образом: Функция максимизируется, если первая производная равна нулю. Продифференцировав функцию совокупной прибыли по , получим уравнение Стратегия по Бертрану предполагает, что … . Модель Бертрана представляет дуополию, в которой идентичные фирмы обладают неизменными средними издержками и назначают цену, стремясь максимизировать собственную прибыль. Каждая из фирм способна полностью удовлетворить рыночный спрос при любой цене, поэтому целью ценовой конкуренции становится вытеснение соперника за пределы рынка путем назначения более низкой (и, следовательно, более привлекательной для покупателя) цены. Такая жесткая ценовая конкуренция часто называется ценовой войной. Дифференциация на рынке отсутствует, взаимодействие происходит одновременно и носит краткосрочный характер. Так как фирмы располагают полной информацией о рынке, каждая из них, прогнозируя действия конкурента, стремится назначить более низкую цену. Предположим, что 1-я фирма назначает цену p1 > p. Аналогично, 2-я фирма стремится назначить p1 < p2. Снижение цены возможно только до уровня издержек на единицу продукции (с), в противном случае исчезает экономический стимул к деятельности в отрасли. Таким образом, единственно возможное равновесие1) в данных условиях p1=p2=c. При этом прибыль фирм П1=П2=c. Таким образом, наблюдается так называемый парадокс Бертрана: фирмы назначают цену на уровне предельных затрат - малое число конкурентов не может манипулировать ценой; высокая концентрация при отсутствии входа новых конкурентов не позволяет воспользоваться монопольной властью; фирмы не получают экономической прибыли, следовательно, отсутствуют стимулы входа на рынок для действующих фирм. Парадоксальная ситуация может быть разрешена, если принять во внимание факторы, характерные для реальных рыночных структур. Рассмотрим, как следующие особенности структуры рынка могут повлиять на стратегическое взаимодействие фирм (при прочих неизменных условиях): асимметрия издержек; ограничение по мощности; дифференциация товара; неполнота информации; долгосрочное взаимодействие фирм. 1. Асимметрия издержек Пусть одна из фирм обладает преимуществом в издержках: Тогда 1-я фирма получает более широкие возможности снижения цены по сравнению со 2-й фирмой. Первая фирма может назначить цену ниже уровня c2: сохраняя при этом положительную прибыль. Исход такой ценовой игры - монополия на рынке. Фирма, обладающая более высокими издержками, не станет вступать в конкурентную борьбу с заранее предопределенным исходом. Рыночная цена будет ниже, чем в ситуации чистой монополии, хотя повышение цены до уровня, максимизирующего монопольную прибыль (так что MR = МС), возможно при отсутствии угрозы возвращения конкурента или входа новых фирм. Таким образом, можно видеть, как характер издержек конкурентов оказывает влияние на взаимодействие фирм и структуру рынка. 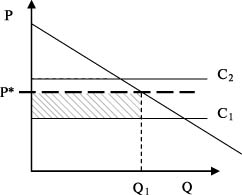 Рис. 5.2 Разрешение парадокса Бертрана при асимметрии издержек Ограничение по мощности Другим случаем разрешения парадокса Бертрана является ограничение по мощности, то есть невозможность удовлетворения рыночного спроса за счет выпуска одной фирмы при цене, близкой к конкурентной (Рс = с). Так, если каждая фирма может выпустить не более qmax, причем объем рыночного спроса QD(P=c) > qmax, ни одной из фирм не выгодно снижать цену до уровня издержек, потому что эта мера не приведет к вытеснению конкурента, но отрицательно повлияет на прибыль. Следовательно, у каждой фирмы существует стимул повышать цену, когда цена конкурента достаточно низка и существует неудовлетворенный спрос на товар (в этом случае фирма может максимизировать прибыль, используя условие MR = МС для остаточного спроса). С другой стороны, при достаточно высоком уровне цены, когда мощность фирмы еще позволяет удовлетворить рыночный спрос целиком, даже небольшое снижение цены по сравнению с конкурентом позволяет полностью завладеть рынком. Появляется противоположенный стимул - к понижению цены. В условиях, когда мощности фирм определены неясным образом, рыночное равновесие не может быть достигнуто (по крайней мере в чистых стратегиях), и колебания цен будут постоянными. Если изменить представление о процессе и добавить предположение, что фирмы способны сами выбирать уровень мощностей, то достижение равновесного состояния рынка становится возможным. Представим ситуацию в виде двухпериодной игры: 1-й период - фирмы определяют объемы производственных мощностей q1, q2; 2-й период - фирмы назначают цены (конкурируют по цене). Решая задачу стандартным методом обратной индукции, получаем, что во втором периоде установится единственно возможное равновесие при цене То есть цена p* обеспечивает продажу максимальных выпусков обеих фирм при выбранных мощностях q1, q2. Решая задачу максимизации прибыли каждой фирмы для первого периода, используем найденное выражение для равновесной цены и получим Таким образом, фирмы сталкиваются с решением задачи Курно - одновременного выбора оптимального выпуска с учетом поведения конкурента. Решением такой задачи станет выпуск, обеспечивающий рыночную цену: где pM - цена при монополии; pC - цена при совершенной конкуренции. При цене p* экономическая прибыль, получаемая фирмами, положительна - парадокс Бертрана разрешен. Мы можем видеть, что случай с выбором мощностей включает как ценовую, так и неценовую (по объему) конкуренцию. Наличие ограничения по мощности снижает остроту ценовой конкуренции, заставляя фирмы взаимодействовать менее агрессивно, вырабатывая стратегии "мирного" сосуществования. Модель олигополии, основанной на тайном сговоре. Все фирмы олигополисты могут заключить тайное соглашение, что ограничит их конкуренцию между собой и предотвратит вступление в отрасль новых фирм. Допустим, что в условиях тайного сговора фирмы-олигополисты производят однородную продукцию и выравнивают цены как в случае их понижения, так и в случае повышения. При этом предельные издержки фирм одинаковы. Тогда их кривая спроса будет неэластичной по цене и фирмам станет выгодно, находясь в сговоре, поддерживать неизменный уровень выпуска, а значит, и неизменные цены. В этом случае положение отрасли напоминает условия чистой, т.е. нерегулируемой монополии. Разновидностью тайного сговора является картель – формальное соглашение фирм по цене и объему выпуска. Жизнь картеля ограничивается выгодностью сговора, основанной на высоком спросе. Как только спрос перестанет расти и начнет снижаться, фирмы будут вынуждены снизить цены, пытаясь вернуться к прежнему объему выпуска с более низкими издержками. Модель Штакельберга Модель асимметричной дуополии, предложенная Г.фон Штакельбергом в 1934 г., представляет развитие моделей количественной дуополии Курно и Чемберлина. Асимметрия дуополии Штакельберга заключается в том, что дуополисты могут придерживаться разных типов поведения - стремиться быть лидером (англ. leader) или оставаться последователем (англ, follower). Последователь Штакельберга придерживается предположений Курно, он следует своей кривой реагирования и принимает решения о прибылемаксимизирующем выпуске, полагая выпуск соперника заданным. Лидер Штакельберга, напротив, не столь наивен, как обыкновенный дуополист Курно, Он настолько изощрен в понимании рыночной ситуации, что не только знает кривую реагирования соперника, но и инкорпорирует ее в свою функцию прибыли, так что последняя принимает вид i = f(qi, Rj, (qi)). А затем он максимизирует свою прибыль, действуя подобно монополисту. Ясно, что в случае дуополии возможны четыре комбинации двух типов поведения. 1. Дуополист 1 - лидер, дуополист 2 - последователь. 2. Дуополист 2 - лидер, дуополист 1 - последователь. 3. Оба дуополиста ведут себя как последователи. 4. Оба дуополиста ведут себя как лидеры. В случаях 1 и 2 поведение дуополистов совместимо, один ведет себя как лидер, другой - как последователь. Здесь не возникает конфликта и исход их взаимодействия стабилен. Случай 3 по сути представляет ситуацию дуополии Курно, оба дуополиста руководствуются своими кривыми реагирования, и исход их взаимодействия стабилен. Нередко поэтому говорят, что модель Курно - это частный случай модели Штакельберга. Ниже приведены основные параметры равновесия Штакельберга:
Графическое решение представлено на рисунке 5.3. 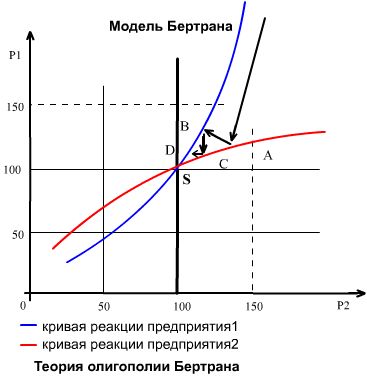 Рис. 5.3 Вывод: … .Все они большие специалисты График предельных издержек фирмы-монополиста задан условием Решение Определяем оптимальный выпуск фирмы-монополиста: MC=MR=Р; 2Q=60-2Q; 4Q=60; Q=15. Выводим функцию спроса фирмы-монополиста: P=a-bQ; Исходя из MR b будет равно 1, а “а”=60. Р=60-Q. Q=60-P. Цена при оптимальном выпуске фирмы-монополиста составит Р=60-15=45. Эластичность Практическое задание 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
