12Понижение порядка линейного однородного уравнения, если известно одно его частное решение. Пусть для линейного уравнения 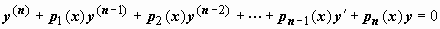 известно частное решение y1(x). Заменой y(x) = z(x) y1(x), это уравнение может быть преобразовано в уравнение, допускающее понижение порядка. Продемонстрируем эту идею на примере уравнения второго порядка известно частное решение y1(x). Заменой y(x) = z(x) y1(x), это уравнение может быть преобразовано в уравнение, допускающее понижение порядка. Продемонстрируем эту идею на примере уравнения второго порядка 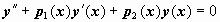 . Пусть y1(x) - частное решение этого уравнения, т.е. . Пусть y1(x) - частное решение этого уравнения, т.е. 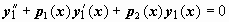 . Перейдём к переменной z(x), связанной с y(x) соотношением y(x)=z(x)y1(x). Тогда . Перейдём к переменной z(x), связанной с y(x) соотношением y(x)=z(x)y1(x). Тогда 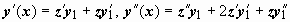 ; подставляем эти выражения в уравнение: ; подставляем эти выражения в уравнение: 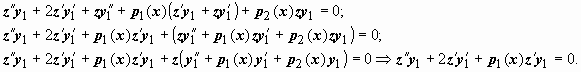
Последнее уравнение не содержит явно неизвестную функцию z(x), поэтому допускает понижение порядка. В рассматриваемом случае уравнения второго порядка получим линейное уравнение первого порядка, которое решается: 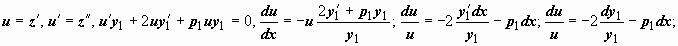
|
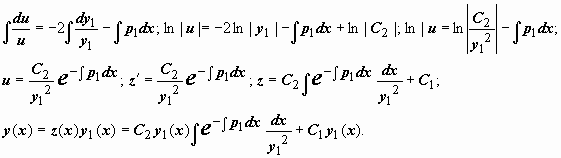
Можно доказать, что вронскиан системы функций 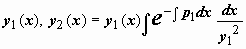 равен , т.е. отличен от нуля и, следовательно, функции y1(x), y2(x) образуют фундаментальную систему решений. Можно, однако, наоборот, получить выражение для y2(x) исходя из этого значения вронскиана, следующего их формулы Лиувилля. Запишемформулу Лиувилля так равен , т.е. отличен от нуля и, следовательно, функции y1(x), y2(x) образуют фундаментальную систему решений. Можно, однако, наоборот, получить выражение для y2(x) исходя из этого значения вронскиана, следующего их формулы Лиувилля. Запишемформулу Лиувилля так 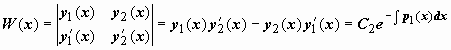 . Поделив это выражение на y1(x), (y1(x))2, получим . Поделив это выражение на y1(x), (y1(x))2, получим 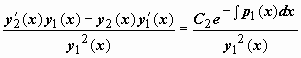 . Выражение слева - производная дроби . Выражение слева - производная дроби 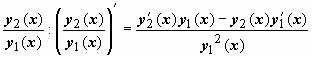 , поэтому , поэтому 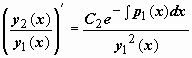 . Интегрируем: . Интегрируем: 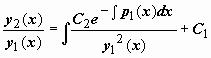 , , 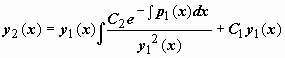 , и так как мы ищем решение y2(x), линейно независимое с y1(x), то берём , и так как мы ищем решение y2(x), линейно независимое с y1(x), то берём 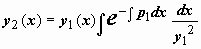 . .
|
12.Восстановление линейного однородного уравнения по фундаментальной системе решений.Пусть дана система функций y1(x), y2(x), …, yn(x) с отличным от нуля на отрезке (a,b) вронскианом W(x). Требуется составить линейное однородноеуравнение, у которого фундаментальная система решений состоит из функций y1(x), y2(x), …, yn(x).
Эта задача решается просто. Так как общее решение этого уравнения должно быть равно y(x) = C1 y1(x) + C2y2(x) + …+ Cnyn(x), система функций y(x), y1(x), y2(x), …, yn(x) линейно зависима, поэтому её определитель Вронского (имеющий порядок n + 1) должен быть равен нулю: 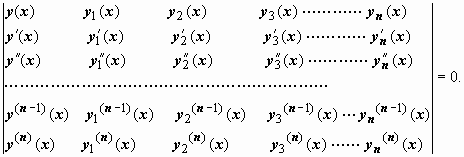
Раскрывая этот определитель по первому столбцу, получим искомое уравнение. Пример: составить линейное уравнение, у которого фундаментальная система решений равна y1(x) = cos x,y2(x)= x3. Решение:
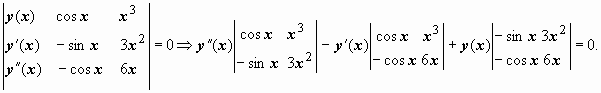
|
Заметим, что коэффициент при старшей производной оказывается равным вронскиану фундаментальной система решений: 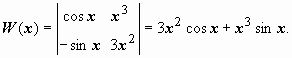 Дальнейшие преобразования дают Дальнейшие преобразования дают 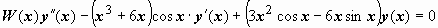 , или , или 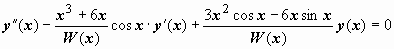 . Это и есть искомое уравнение. Его коэффициенты непрерывны на любом интервале, на котором . Это и есть искомое уравнение. Его коэффициенты непрерывны на любом интервале, на котором 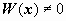 . .
|
13) Структура общего решения линейного неоднородного ОДУ n-ого порядка.
Рассмотрим на [a; b] линейное однородное дифференциальное уравнение
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0.
Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C1,..., Cn ), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям :
− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn ) является решением уравнения на [a; b] ;
− какова бы ни была начальная точка (x0, y0, y1,0 ,..., yn − 1,0 ) , x0∈ [a;b] , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) = y1,0 ,..., y(n − 1) (x0) = yn− 1,0 .
Справедливо следующее утверждение (теорема о структуре общего решения линейного однородного уравнения): Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид
y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) + ... + Cn yn(x),
где C1,...,Cn — произвольные постоянные.
Метод вариации постоянных для поиска частных решений линейного неоднородного ОДУ n-ого порядка.
Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью.
Рассмотрим линейное неоднородное дифференциальное уравнение
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x).
с непрерывными на [a; b] коэффициентами и непрерывной правой частью.
Предположим, что известна фундаментальная система y1(x), y2(x),..., yn(x) решений соответствующего однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0.
Будем искать частное решение неоднородного уравнения в виде
y*(x) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) ,
где C1(x), C2(x) , ... , Cn(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.
|
Справедливо следующее утверждение.
Пусть y1(x), y2(x),..., yn(x) — фундаментальная система решений однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде
y*(x) = y(x,C1,..., Cn) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) .
Неизвестные функции C1(x), C2(x) , ... , Cn(x) находятся из системы
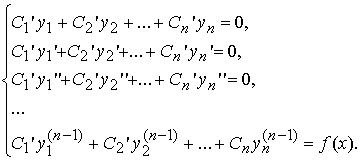
Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянныхили методом Лагранжа.
|
14.Линейные однородные ОДУ n-ого порядка с постоянными коэффициентами. Метод Эйлера нахождение решений. Характеристический многочлен.
Случай
Линейное однородное уравнение n-го порядка с постоянными коэффициентами
Уравнение n-го порядка для одной неизвестной функции z независимого переменного t с постоянными коэффициентами имеет вид:
где a1,,an - постоянные числа (действительные или комплексные). К уравнению (2.1), очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. (См. соответствующую формулировку в первом параграфе первой главы). Решения уравнения (2.1) будут построены в явном виде и тем самым установлена еще раз теорема существования. Теорема единственности будет использоваться по существу для доказательства того, что найдены все решения данного уравнения.
Прежде, чем приступить к решению уравнения (2.1) условимся о некоторых обозначениях и понятиях.
Производную по времени от произвольной функции z = z(t) удобно обозначать через pz = p(z), трактуя символ p как линейную операцию над функцией z:
Тогда натуральная степень k операции p, обозначаемая через pk, естественно понимается как 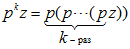 и представляет собой производную k-го порядка от функции z: и представляет собой производную k-го порядка от функции z:
Ясно, что степень pk операции p подчиняется формальным алгебраическим правилам
Естественным представляется определение операции cpk, где c - число и суммы pk + pm:
Пользуясь введенными обозначениями, мы можем записать левую часть уравнения (2.1) в виде
Положим
Данное выражение в соответствии с равенством (2.5) представляет собой линейную операцию над функцией z, т.е.
С другой стороны само выражение (2.6) представляет собой выражение относительно символа p с постоянными (действительными или комплексными) коэффициентами, для которого справедливы обычные алгебраические правила оперирования, т.е. если L(p) и M(p) - два произвольных многочлена относительно символа p (или, как говорят, оператора дифференцирования p), то
|
|
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривойкусочно линейной функцией, т. н. ломаной Эйлера.
Описание метода
Пусть дана задача Коши для уравнения первого порядка
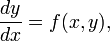
где функция f определена на некоторой области . Решение разыскивается на интервале (x0,b]. На этом интервале введем узлы
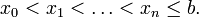
Приближенное решение в узлах xi, которое обозначим через yi определяется по формуле
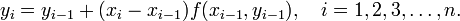
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
Оценка погрешности
Метод Эйлера является методом первого порядка. Если функция f непрерывна в D и непрерывно дифференцируема по переменной y в D, то имеет место следующая оценка погрешности
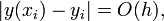
где h — средний шаг, то есть существует C > 0 такая, что 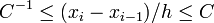 . .
Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.
ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН
матрицы 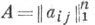 над полем К - многочлен над полем К над полем К - многочлен над полем К
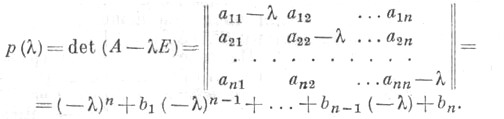
Степень X. м. равна порядку квадратной матрицы А, коэффициент b1 равен следу матрицы .(b1 = tr A = a11+ а 22+ .. . +а пп),коэффициент b т равен сумме всех главных миноров т- гопорядка, в частности bn=detA. Уравнение 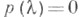 наз. характеристическим уравнением матрицы А, или вековым уравнением. наз. характеристическим уравнением матрицы А, или вековым уравнением.
Корни X. м., лежащие в К, наз. характеристическими значениями или собственными значениями матрицы А. Если К - числовое поле, употребляются также термины лхарактеристические числа
частности bn=detA. Уравнение 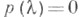 наз. характеристическим уравнением матрицы А, или вековым уравнением. наз. характеристическим уравнением матрицы А, или вековым уравнением.
Корни X. м., лежащие в К, наз. характеристическими значениями или собственными значениями матрицы А. Если К - числовое поле, употребляются также термины лхарактеристические числа
| |
 Скачать 0.93 Mb.
Скачать 0.93 Mb.