Контрольная работа. Решение Разложение частного решения дифференциального уравнения при начальном условии имеет вид
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
Контрольная работа (2-й семестр) Задача 7. Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения 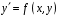 , удовлетворяющего начальному условию , удовлетворяющего начальному условию 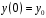 . .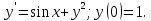 Решение Разложение частного решения В данном случае 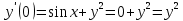 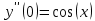 = 1 = 1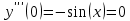 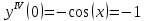 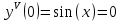 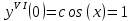 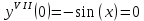 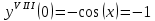 Следовательно, получили разложение y(x)=1 + 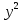 x+ x+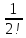 x2 + 0x3 ‒ x2 + 0x3 ‒ 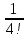 x4 + 0x5 + x4 + 0x5 + 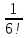 x6 + … = 1 + x6 + … = 1 + 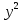 x+ x+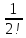 x2 ‒ x2 ‒ 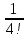 x4 + x4 + 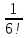 x6 ‒ x6 ‒ 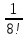 x8 … x8 …Ответ: три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения: 1, 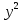 x, x, 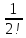 x2 x2Задача 8. Найти общее решение дифференциального уравнения. 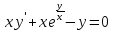 Решение. Дано дифференциальное уравнение: 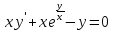    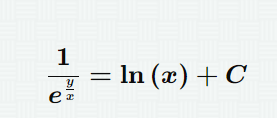 Ответ: исходное дифференциальное уравнение 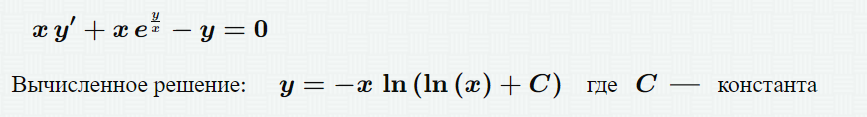 Задача 9. Найти частное решение дифференциального уравнения 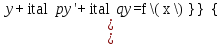 , удовлетворяющее начальным условиям , удовлетворяющее начальным условиям 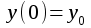 , , 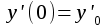 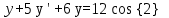 ; ; 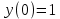 , , 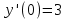 . .Решение. Запишем данное дифференциальное уравнение в виде: 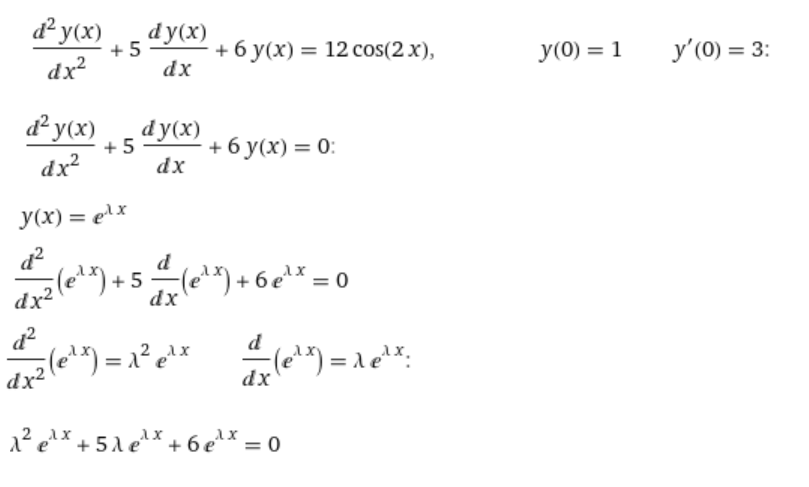 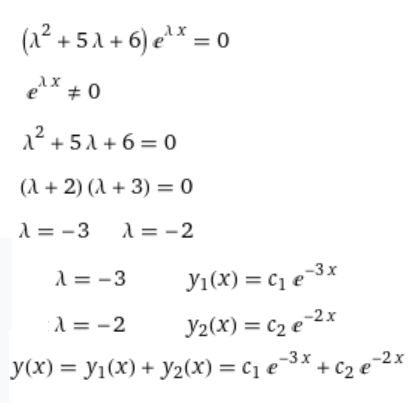 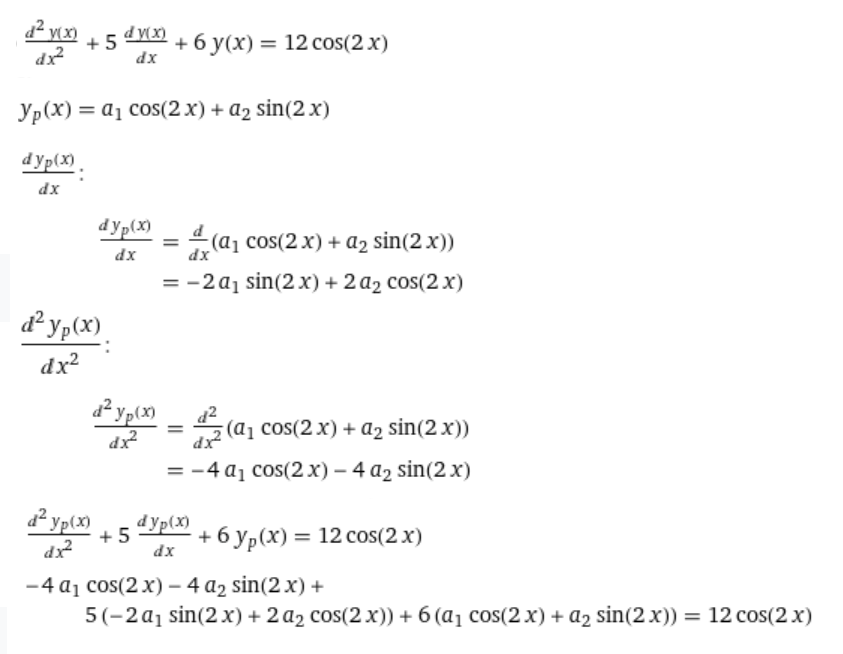 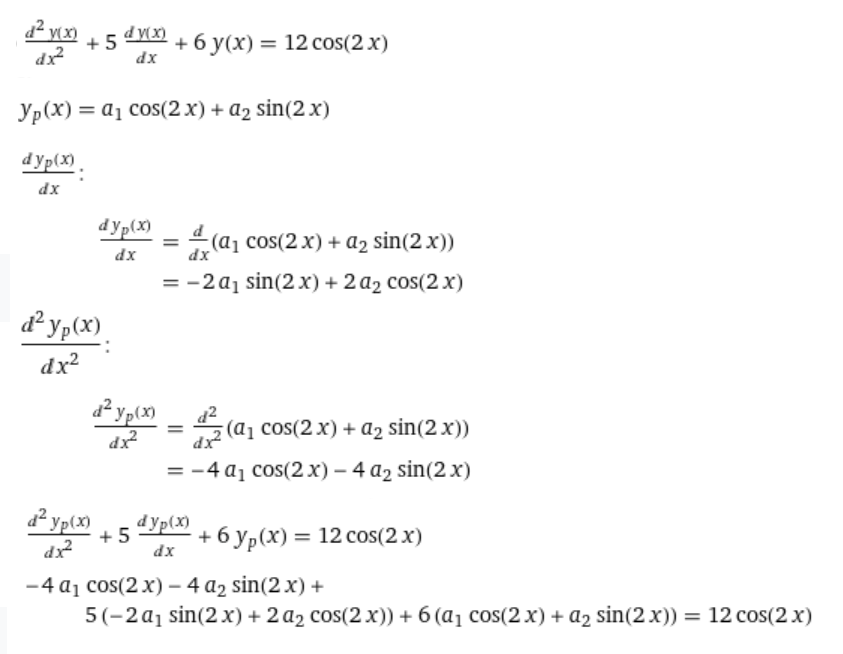 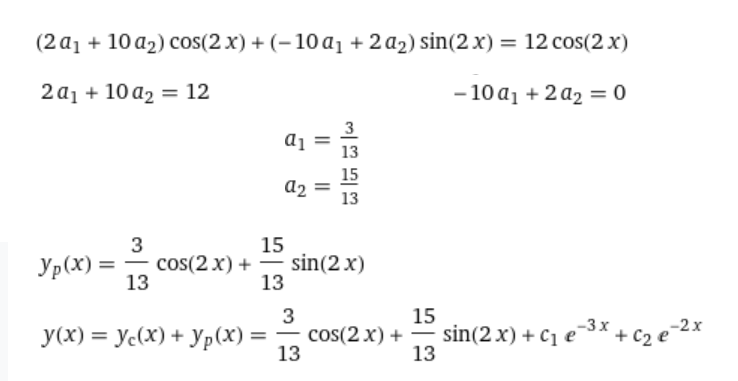 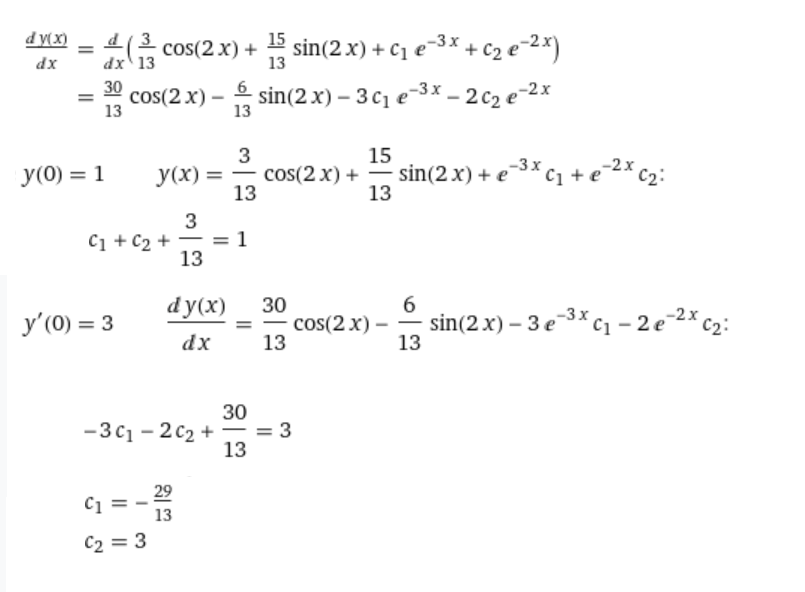 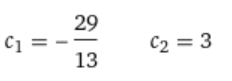 подставляем в подставляем в 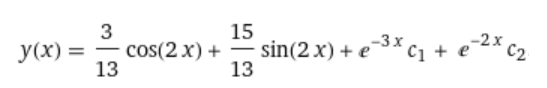 Ответ: Задача 10. Дана функция 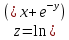 . . Показать, что 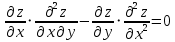 . . Решение 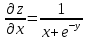 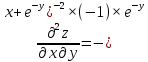 = =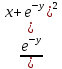 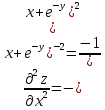 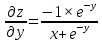 Тогда, подставив найденные значения в 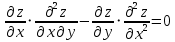 , получим , получим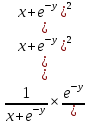 = = 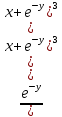 = 0 = 0Ответ: данное тождество выполнено для заданной функции Задача 11. Найти наименьшее и наибольшее значения функции z=f(x, y) в замкнутой области D, заданной системой неравенств. Сделать чертеж. z=x2+2xy +2y2; -1≤x≤1, 0≤y≤2. Решение 1. Найдем частные производные. 2. Решим систему уравнений. 2×x+2×y = 0 2×x+4×y = 0 Получим: а) Из первого уравнения выражаем x и подставляем во второе уравнение: x = ‒2×y ‒2×y = 0 Откуда y = 0 Данные значения y подставляем в выражение для x, получаем: x = 0 Количество критических точек равно 1: M1(0;0) 3. Найдем частные производные второго порядка. 4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0). Вычисляем значения для точки M1(0;0) AC - B2 = 4 > 0 и A > 0 , то в точке M1(0;0) имеется минимум z(0;0) = 0 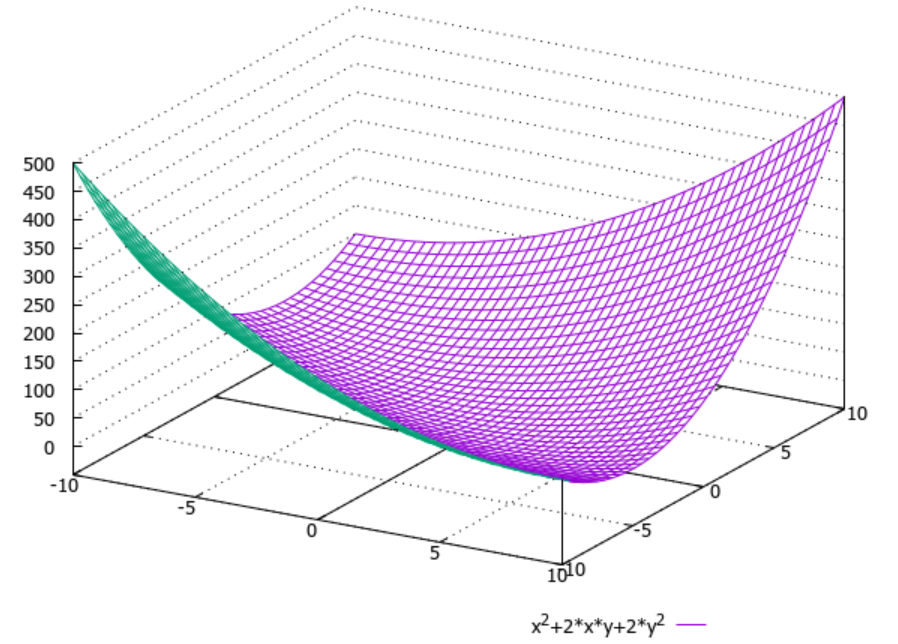 Ответ: в точке M1(0;0) имеется минимум z(0;0) = 0; Задача 12. Дана функция z=z(x, y), точка А(х0, у0) и вектор 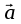 . Найти: 1) . Найти: 1) 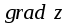 в точке A; 2) производную в точке A по направлению вектора в точке A; 2) производную в точке A по направлению вектора 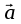 . .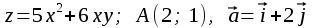 . .Решение Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.: Находим частные производные: Тогда величина градиента равна: Полный дифференциал функции: dU=(10·x+6·y)·dx + 6·x·dy Найдем градиент в точке А(2;1) Модуль grad(z) - наибольшая скорость возрастания функции: Направление вектора-градиента задаётся его направляющими косинусами: 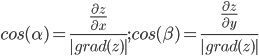 Задача 13. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равно 0,9, второе – 0,95 и третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства. Решение а) только одно устройство (сработать может или 1-ое устройство, 2, 3 при этом не сработает, или 2-ое сработает, 1, 3 при этом не сработают, или 3-ие устройство сработает, а 1,2 не сработает): Р1(А)= 0,9 × (1 ‒ 0,95) × (1 ‒ 0,85) + (1 ‒ 0,9) × 0,95 × (1 ‒ 0,85) + + (1 ‒ 0,9) × (1 ‒ 0,95) × 0,85 = 0,00675 + 0,01425 + 0,00425 =0,02525 б) только два устройства (сработать могут или 1-ое и 2-ое устройство, 3 при этом не сработает, или 2-ое и 3-ие сработают, 1-ое при этом не сработают, или 1-ое и 3-ие устройство сработает, а 2 не сработает): Р2(А)= 0,9 × 0,95 × (1 ‒ 0,85) + (1 ‒ 0,9) × 0,95 × 0,85 + + 0,9 × (1 ‒ 0,95) × 0,85 = 0,12825 + 0,08075 + 0,03825 =0,24725 в) все три устройства Р3(А)= 0,9 × 0,95 × 0,85 = 0,72675 Ответ: Р1(А)= 0,02525, Р2(А)= 0,24725, Р3(А)= 0,72675 Задача 14. Случайная величина Х задана функцией распределения (интегральной функцией) F(x). Найти плотность вероятности (дифференциальную функцию), математическое ожидание и дисперсию. Построить графики интегральной и дифференциальной функций. 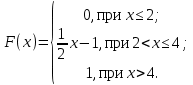 Решение Случайная величина Х задана функцией распределения F(x): 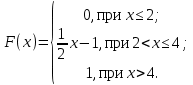 Найдем плотность распределения f(x), как производную от функции распределения F(x): f(x) = dF(x)/dx = ½ Плотность распределения f(x): 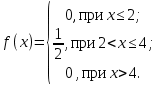 Математическое ожидание: Дисперсия: Среднеквадратическое отклонение: Графики интегральной и дифференциальной функций: 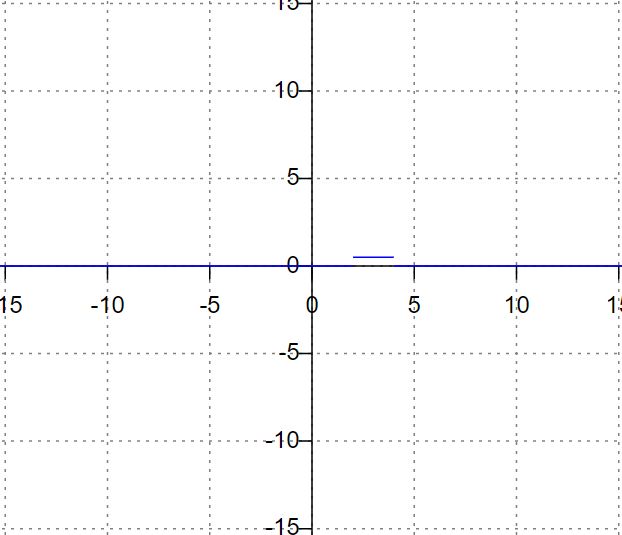 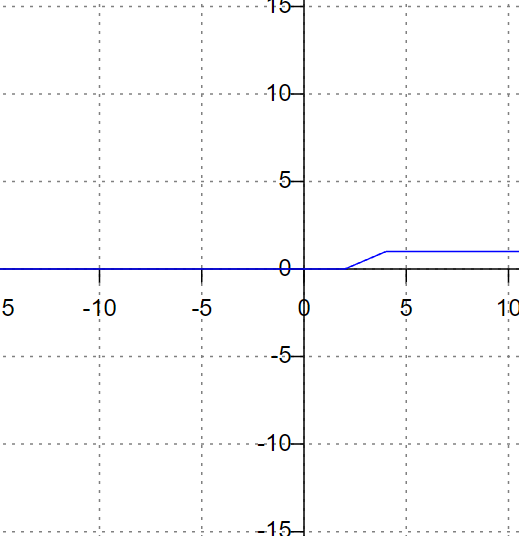 Задача 15. Найти доверительный интервал для оценки математического ожидания a нормального распределения с надёжностью 0,96, зная выборочную среднюю 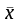 . Объем выборки n и среднее квадратическое отклонение σ. . Объем выборки n и среднее квадратическое отклонение σ.Решение Стандартная ошибка выборки: Доверительный интервал для генерального среднего: Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа. В этом случае 2Ф(tkp) = γ Ф(tkp) = γ/2 = 0,96/2 = 0,48 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0,48 tkp(γ) = (0,48) = 2,06 (75,13 – 2,06; 75,13 + 2,06) = (73,07; 77,19) Ответ: с вероятностью 0,96 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала (73,07; 77,19) |
