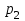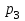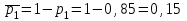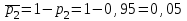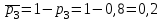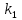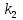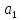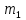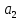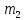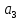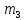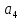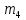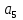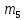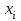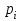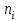045теоия вероят. Решение Вероятность, что сработает Вероятность, что не сработает 1 устройство
 Скачать 182.75 Kb. Скачать 182.75 Kb.
|
|
6) Для сигнализации на складе установлены три независимо работающих устройства. Вероятность того, что при необходимости первое устройство сработает, составляет 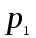 , для второго и третьего устройства эти вероятности равны соответственно , для второго и третьего устройства эти вероятности равны соответственно 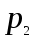 и и 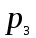 . Найти вероятность того, что в случае необходимости сработают: . Найти вероятность того, что в случае необходимости сработают:а) все устройства; б) только одно устройство; в) хотя бы одно устройство.
Решение:
а) обозначим за А- сработают все устройства, тогда: Р(А)=р1·р2·р3=0,85·0,95·0,8=0,646 б) обозначим за В- сработает только одно устройство, тогда: В1-сработает первое устройство Р(В1)= 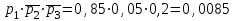 В2-сработает второе устройство Р(В2)= 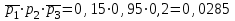 В3-сработает третье устройство Р(В3)= 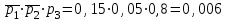 Р(В)=Р(В1)+Р(В2)+Р(В3)=0,0085+0,0285+0,006=0,043 в) обозначим за С – сработает хотя бы одно устройство, тогда: противоположное ему событие  - ни одно из устройств не сработает, тогда: - ни одно из устройств не сработает, тогда:Р(  )= )=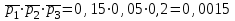 Р(С)=1- Р(  )=1-0,0015=0,9985 )=1-0,0015=0,9985Ответ: а) 0,646 б) 0,043 в) 0,9985 14) В ювелирный магазин изделия поступают от трех разных изготовителей в соотношении: m% всех поступающих изделий, составляют изделия первого изготовителя, n% – второго, остальные изделия третьего изготовителя. Вероятность того, что изделие, произведённое первым изготовителем, имеет скрытый дефект, равна  , для второго и третьего изготовителей эти вероятности равны соответственно , для второго и третьего изготовителей эти вероятности равны соответственно 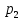 ,и ,и  ,. ,. а) Найти вероятность того, что наудачу выбранное изделие имеет скрытый дефект. б) Оказалось, что наудачу выбранное изделие имеет скрытый дефект. Какова вероятность того, что оно произведено вторым изготовителем?
Решение: обозначим: событие А –изделие имеет скрытый дефект; событие Н1 –изделие от 1 производителя; событие Н2 – изделие от 2 производителя; событие Н3 – изделие от 3 производителя. По условию задачи 45% всех изделий поступает от 1 производителя, следовательно Р(Н1) = 0,45, от 2 производителя – 35%, тогда Р(Н2) = 0,35 и от 3 производителя оставшиеся 20 % всех изделий, то есть Р(Н3) = 0,20. Очевидно, что P(H1) + P(H2) + P(H3) = 0,45+0,35+0,2=1. Вероятность того, что изделие, произведённое первым изготовителем, имеет скрытый дефект, равна 0,01, т.е. РН1(А)=0,01; вторым производителем – 0,05, т.е.РН2(А)=0,05 и третьим производителем – 0,01, т.е. РН3(А)=0,01. а) Учитывая, что событие А произойдет обязательно с одним из событий (гипотез) Нi , образующих полную группу, применим формулу полной вероятности: Р(А)= Р(Н1)· РН1(А)+ Р(Н2)· РН2(А)+ Р(Н3)· РН3(А)=0,45·0,01+0,35·0,05+ +0,20·0,01=0,0045+0,0175+0,002=0,024 б) Пусть оказалось, что случайно выбранное изделие имеет скрытый дефект. Найдём вероятность того, что оно произведено вторым изготовителем (гипотеза Н2). Используем для этого формулу Байеса: 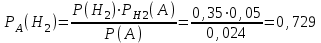 Ответ: Р(А)=0,024; РА(Н2)=0,729. 27) Вероятность того, что в результате проверки изделию будет присвоен знак «изделие высшего качества» равна p. 1. На контроль поступило n изделий. Какова вероятность того, что знак высшего качества будет присвоен ровно m изделиям. 2. При тех же условиях найти вероятность того, что в партии из N изделий знак высшего качества получат: а) ровно kизделий; б) не менее чем k1 , но не более, чем k2изделий.
Решение: вероятность того, что будет присвоен знак высшего качества по условию равен р=0,3. тогда вероятность того, что знак не будет присвоен q=1-р=1-0,=0,7. А=  ровно 1 изделию присвоен знак высшего качества ровно 1 изделию присвоен знак высшего качества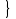 по формуле Бернулли находим: Р(А)=Р5(2)= 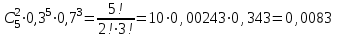 2) по условию N=30 р=0,3 q=0,7 а) Найдем вероятность Р30(12) приближенно с помощью локальной формулы Лапласа: 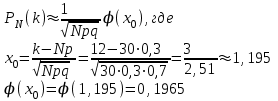 Тогда Р30(12) 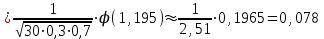 б) вероятность того, что число попаданий будет не менее 8, но не более 20, вычисляем по формуле Лапласа: 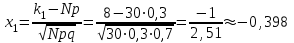 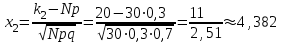 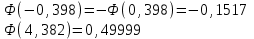 Тогда Р30(8;20) 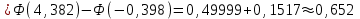 Ответ: 1) 0,0083 2) а) 0,078 б) 0,652 35) В лотерее на каждые 100 билетов приходится m1 билетов с выигрышем a1тыс. рублей, m2 билетов с выигрышем a2 тыс. рублей, m3 билетов с выигрышем a3 тыс. рублей и т.д. Остальные билеты из сотни не выигрывают. Составить закон распределения величины выигрыша для владельца одного билета и найти его основные характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение. Пояснить смысл указанных характеристик.
Решение: Число выигрышных билетов из 100 составляет: 5+10+12+15+18=60, значит, число невыигрышных билетов:100 – 60 =40. Согласно закону распределения х принимаем значения: х1=0 – невыигрышный билет, х2=5– выигрыш в 10 тыс.руб., х3= 2 в 8 тыс.руб., х4=12 в 6 тыс.руб., х5=15 в 4 тыс.руб., х6=18 в 2 тыс.руб. Соответствующие вероятности будут: 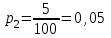 (где 5 - число выигрышей по 10 тыс. рублей, 100-общее количество билетов), (где 5 - число выигрышей по 10 тыс. рублей, 100-общее количество билетов), 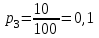 , , 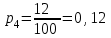 , , 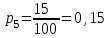 , , 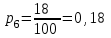 р1= 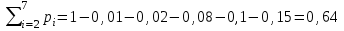
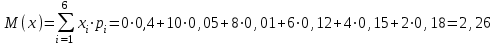 Таким образом, ожидаемый средний выигрыш на 1 билет составляет 2,26 т. р. Дисперсию случайной величины найдем двумя способами: 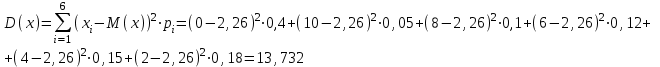 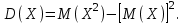 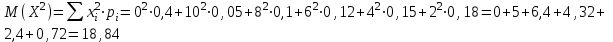 Тогда: Тогда: 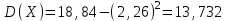 Очевидно, что результаты вычислений дисперсии по обоим способам совпадают. Среднее квадратичное отклонение: 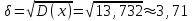 Таким образом, =3,71 т. р. – характеристика разброса фактических значений выигрыша от найденного среднего значения, а =2,26 т. р. Это означает, что основные значения случайной величины выигрыша находятся в диапазоне 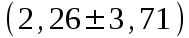 т. р., что соответствует данным задачи. т. р., что соответствует данным задачи.Ответы.М (Х) = 2,26; D(Х) = 13,732; (Х) =3,71. 47) Вес одной порции мясного блюда должен составлять, а гр. В процессе приготовления возникают случайные погрешности, в результате которых вес порционного блюда является случайной величиной подчиненной нормальному закону распределения со средним квадратическим отклонением гр. Найти вероятность того, что: а) вес изделия составит от до гр.; б) величина погрешности веса будет менее гр.
Решение: а) 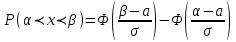 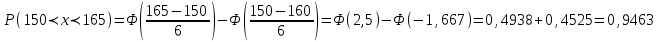 Ф(2,5)=0,4938, Ф(-1,667)=-Ф(1,667)=-0,4525 Ф(2,5)=0,4938, Ф(-1,667)=-Ф(1,667)=-0,4525б) 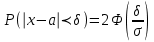 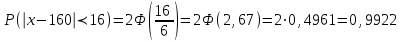 (99,22%) (99,22%)Ф(2,66)=0,4961 Ответ: а) 0,9463 б) 0,99,22 59) По итогам выборочных обследований, для некоторой категории сотрудников, величина их месячного заработка xi тыс. рублей .и соответствующее количество сотрудников ni представлены в виде интервального статистического распределения. а) Построить гистограмму относительных частот распределения. б) Найти основные характеристики распределения выборочных данных: среднее выборочное значение, выборочную дисперсию и выборочное среднее квадратическое отклонение. в) Оценить генеральные характеристики по найденным выборочным характеристикам точечным образом. г) Зная, что значения признака X в генеральной совокупности подчинены нормальному закону распределения, найти доверительный интервал для оценки математического ожидания (генерального среднего значения) с надежностью считая, что генеральная дисперсия равна исправленной выборочной дисперсии.
Решение: Найдем объем выборки n: 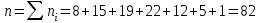 то есть для обследования выбрано 85 сотрудников. а) Вычислим относительные частоты для каждого частичного интервала: 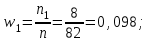 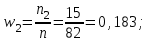 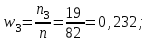  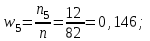 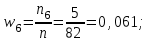 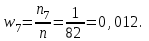 Контроль: 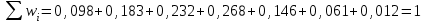 В итоге получено следующее интервальное распределение относительных частот признака X:
Шаг разбиения h это длина каждого частичного интервала: h=3. Строим гистограмму относительных частот. На графике по горизонтальной оси ОX отложены частичные интервалы для признака X, а по вертикальной оси – значения относительных частот wi. 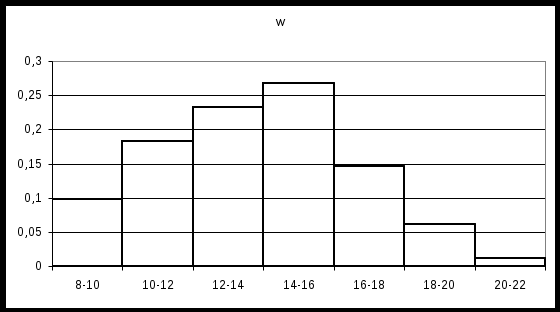 б) Для нахождения характеристик выборки от заданного интервального распределения признака X перейдем к дискретному распределению, выбирая в качестве значений признака xi середины частичных интервалов:
Найдем основные характеристики этого распределения. Средняя выборочная (средняя месячная заработная плата в т. р.): 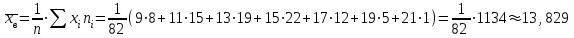 Выборочная дисперсия: Выборочная дисперсия: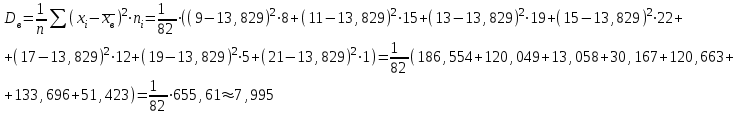 Рассмотрим второй способ вычисления дисперсии. Найдем среднее квадратов значений признака: Рассмотрим второй способ вычисления дисперсии. Найдем среднее квадратов значений признака: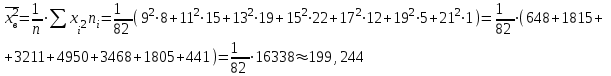 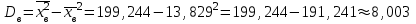 Этот результат совпадает с результатом первого способа (иногда приближенно из-за округлений). Выборочное среднее квадратическое отклонение: 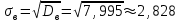 то есть, в среднем составляет ± 2,828 тыс. рублей от среднего значения 7,995 тыс. рублей. в) Оценим неизвестные генеральные характеристики. Генеральное среднее значение: 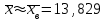 т. р. т. р.Генеральная дисперсия: 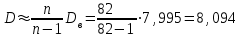 тыс.руб. тыс.руб.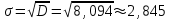 г) Доверительный интервал для оценки генеральной средней a(средней зарплаты) с надежностью γ находим по формуле: 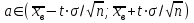 По условию задачи n =82; 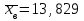 ; ;  , γ = 0,98. Неизвестный параметр t находим из условия: 2Φ(t) = γ. Поскольку в данной задаче γ = 0,98, то есть 2Φ(t) = 0,98, то Ф(t) = 0,49. По таблице Приложения 2, находим t = 2,34. , γ = 0,98. Неизвестный параметр t находим из условия: 2Φ(t) = γ. Поскольку в данной задаче γ = 0,98, то есть 2Φ(t) = 0,98, то Ф(t) = 0,49. По таблице Приложения 2, находим t = 2,34.Вычислим по этим данным доверительный интервал: 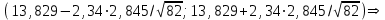 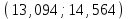 Таким образом, с вероятностью 98% неизвестная генеральная средняя (математическое ожидание) находится в этом интервале: x = a∈(13,094; 14,564). Ответ: 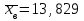 , , 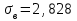 , , 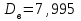 , , 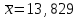 , , 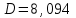 , ,  62) С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X – величина месячной прибыли в т. р., Y – месячные издержки в процентах к объему продаж. Результаты выборки представлены в виде таблицы. По данным выборки: а) оценить тесноту линейной связи между признаками Х и Y; б) найти зависимость между признаками в виде уравнения линейной регрессии 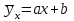 ; ;в) построить графически наблюдаемые выборочные значения признаков и прямую регрессии. г) Используя уравнение линейной регрессии, спрогнозировать величину месячных издержек в процентах к объему продаж, если величина месячной прибыли будет составлять Х = K т. р.
Решение: По условию имеется n=5 наблюдений для соответственных значений признаков Х и Y. Найдем средние значения признаков 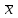 и и 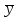 , а также их средние квадратические отклонения σх и σу по тем же формулам, что и в предыдущей задаче, но с учетом того, что каждое значение признака встречается только один раз, то есть все ni = 1. , а также их средние квадратические отклонения σх и σу по тем же формулам, что и в предыдущей задаче, но с учетом того, что каждое значение признака встречается только один раз, то есть все ni = 1.Вычисления будем вести с точностью до 0,001. 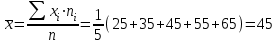 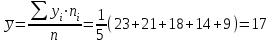 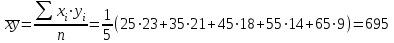 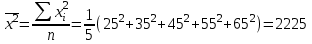 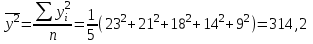 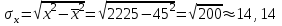 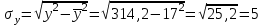 а) Оценим тесноту линейной связи по коэффициенту линейной корреляции r: 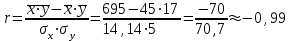 Так как r < 0, то связь обратная, то есть с ростом значений признака Х значения признака Y убывают. Так как 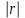 = =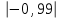 = 0,99, то по шкале Чаддока, определяем, что линейная связь очень высокая. = 0,99, то по шкале Чаддока, определяем, что линейная связь очень высокая.б) Найдем уравнение линейной регрессии. Его параметры: 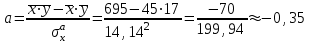 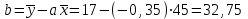 В результате получим, что среднее значение издержек 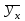 связано с величиной прибыли х уравнением: связано с величиной прибыли х уравнением: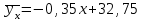 в) Изобразим графически данные значения (хi; уi) в виде точек на плоскости хОу (Рис. 4). Прямую регрессии у = –0,35х +32,75 строим по двум точкам: х = 0; у = – 0,35*0 +32,75 =32,75. х = 65; у = –0,35*70 +32,75 =8,25. Получены точки (0;32,75) и (70;8,25). 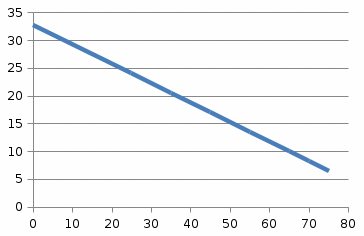 На графике прямая регрессии убывает и проходит через точку A( 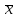 ; ; 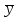 ), то есть (70;8,25). Прямая регрессии Прямая регрессии наилучшим образом приближена ко всем данным точкам, которые расположены вблизи прямой по обе стороны от нее. ), то есть (70;8,25). Прямая регрессии Прямая регрессии наилучшим образом приближена ко всем данным точкам, которые расположены вблизи прямой по обе стороны от нее.г) Используя найденную зависимость, спрогнозируем величину месячных издержек, если месячная прибыль составит 75 тыс. руб.: у=-0,35*75+32,75=6,5, т.е. 6,5% к объему продаж. Ответ. Корреляционная зависимость между признаками Х и Y очень высокая, ее можно описать линейным уравнением регрессии: у = –0,35х + 32,75. Прогнозируемые издержки составят 6,5 % к объёму продаж. Список используемой литературы 1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2006. – 479 с. 2. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2003. –543 с. 3. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. - М.: Айрис-пресс, 2006.-288с. 4. Кузнецов Б.Т. Математика: Учебник для студентов вузов, обучающихся по специальностям экономики и управления. – М.: ЮНИТИ-ДАНА, 2004 . – 719 с. 5. Гмурман В.Е. Руководство к решению задач по теории вероят-ностей и математической статистике. – М.: Высшая школа, 2001. –400 с. 6. Красс М.С. Основы математики и ее приложения в экономическом образовании: Учебник / М.С. Красс, Б.П. Чупрынов. – М.: Дело, 2001. – 688 с. 7. Теория вероятностей. Задания для практических занятий / Сост.В.Г. Чередниченко– Новосибирск: СибУПК, 2006. – 32 с. |