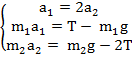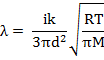физика задачи. физика-задачи. Решение s a bt Ct 2 Dt 3 a 6 м b 3 мс c 2 мс 2 d 1 мс 3 t 1 1 c
 Скачать 6.65 Mb.
|
|
Задача № 1.18 Зависимость пройденного телом пути от времени задается уравнением s = A – Bt + Ct2 + Dt3 (A = 6 м, B = 3 м/с, C = 2 м/с2, D = 1 м/с3). Определите для тела в интервале времени от t1 = 1 c до t2 = 4 c 1) среднюю скорость, 2) среднее ускорение.
Задача № 1.34 Колесо вращается с постоянным угловым ускорением ε = 3 рад/с. Определите радиус колеса, если через t = 1 c после начала движения полное ускорение колеса a = 7,5 м/с2.
Задача №1.48 На рисунке изображена система блоков, к которым подвешены грузы массами m1 = 200 г и m2 = 500 г. Считая, что груз m1 поднимается, а подвижный блок с m2 опускается, нить и блоки невесомы, силы трения отсутствуют. Определите: 1) силу натяжения нити Т 2) ускорения, с которыми движутся грузы.
Задача № 1.68 На железнодорожной платформе, движущейся по инерции со скоростью U0 = 3 км/ч, укреплено орудие. Масса платформы с орудием M = 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m = 10 кг вылетает из ствола под углом α = 600 к горизонту. Определите скорость U снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в n = 2 раза.
Задача № 1.100 К нижнему концу пружины жесткостью k1 присоединена другая пружина жесткостью k2, к концу которой прикреплена гиря. Пренебрегая массой пружины, определите отношение потенциальных энергий пружин.
Задача № 1.117 Зависимость потенциальной энергии П тела в центральном силовом поле от расстояния r до центра поля задается функцией П(r) = , (A = 6 мкДж *м2 и B = 0,3 мДж *м). Определите, при каких значениях r максимальное значение принимают: 1)потенциальная энергия тела 2) сила, действующая на тело.
Задача № 1.146 Маховик в виде сплошного диска, момент инерции которого J = 1,5 кг*м2, вращаясь при торможении равно замедленно, за время t = 1 мин уменьшил частоту своего вращения с n0 = 240 об/мин до n1 = 120 об/мин. Определите: 1) угловое ускорение ε маховик 2) момент М силы торможения 3) работу торможения А.
Задача № 1.161 Платформа, имеющая форму сплошного однородного диска, может вращаться вокруг неподвижный вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определите, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.
Задача № 1.184 На экваторе некоторой планеты (плотность планеты  ) тела весит в два раза меньше, чеми на полюсе. Определите период обращения планеты вокруг собственной оси.
Задача № 1.201 К потолку вагона, движущегося в горизонтальном направлении с ускорением a = 9,81 м/с2, подвешен на нити шарик массой m = 200 г. Определите для установивщегося движения: 1) силу натяжения нити Т, 2) угол отклонения нити от вертикали.
Задача № 1.237 Смесь свинцовых дробинок (плотность = 11,3 г/см3) диаметром 4 мм и 2 мм одновременно опускают в широкий сосуд глубиной, h = 1,5 м с глицерином (плотность I = 1,26 г/cм3, динамическая вязкость ᵑ = 1,48 Пa * c). Определите, на сколько больше времени потребуется дробинкам меньшего размера, чтобы достичь дна сосуда.
Задача № 1.277 Определите кинетическую энергию электрона, если полная энергия движущегося электрона втрое больше его энергия покоя. Ответ выразите в электрон – вольтах.
Задача № 4.57 Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x = 3 cos2ꙍt, см и y = 4 cos(2ꙍt +π), см. Определите уравнение траектории точки и вычертите ее с нанесением масштаба.
Задача № 4.73 За время, в течение которого система совершает N = 50 полных колебаний, амплитуда уменьшается в 2 раза. Определите добротность Q системы.
Задача № 4.148 Средняя квадратичная скорость молекул двухатомного газа при некоторых условиях составляет 480 м/с. Определите скорость распространения звука в газе при тех же условиях.
Задача № 2.26 Каково давление воздуха в шахте на глубине 1 км, если считать, что температура по всей высоте постоянная и равна 220C, а ускорение свободного паданеия не зависит от высоты ? Давление воздуха у поверхности Земли примите равны p0
Задача № 2.38 Пространство между двумя параллельными пластинами площадью 150 см2 каждая, находящимися на расстоянии 5 мм друг от друга, заполнено кислородом. Одна пластина поддерживается при темсперате 170C, другая – при температуре 270C. Определите количество теплоты, прошедшее за 5 мин посредством теплопроводимости от одной пластины к другой. Кислород находится при нормальных условиях. Эффективный диаметр молекул кислорода считать равным 0,36 мм.
Задача № 2.59 Кислород объемом 1 л находится под давлением 1 МПа. Определите, какое количество теплоты необходимо сообщить газу, чтобы: 1) увеличить его объем вдвое в результате изобарного процесса; 2) увеличить его давление вдвое в результате изохорного процесса.
Задача № 2.73 Рабочее тело - идеальный газ - теплового двигателя совершает цикл, состоящий из последовательных процессов изобарного адиабатного и изотермического. В результате изобарного процесса газ нагревается T1 = 300 K до T2 = 600 K. Определите термический КПД теплового двигателя.
Задача № 2.106 Капилляр, внутренний радиус которого 0,5 мм, опущен в жидкость. Определите массу жидкости, поднявшейся в капилляре, если ее поверхностное натяжение равно 60 мН/м.
Задача № 3.54 К пластинам плоского водушного конденсатора приложена разность потенциалов U 1 = 500 B. Площадь пластин S = 200 см2, расстояние между ними d = 1,5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли парафин (ε = 2). Определите разность потенциалов U2 между пластинами после внесених диэлектрика. Определите также емкости конденсатора C1 и C2 до и после внесения диэлектрика.
Задача № 3.66 Сплошной эбонитовых шар (ε = 3) радиусом R = 5 см заряжен равномерно с объемной плотность = 10 нК/м3. Определите энергию электрического поля, заключенную внутри шара.
Задача № 3.83 Через лампу накаливания течет ток, равный 0,6 А. Температура вольфрамовой нити диаметром 0,1 мм равна 2200 0C. Ток подводится медным проводом сечением 6 мм2. Определите напряженность электрического поля: 1) в вольфраме (удельное сопротивление при 00 С = 55 нОм*м, температурный коэффициент сопротивления α = 0,0045 0C-1) 2)в меди ( = 17 нОм*м).
Задача № 3.96 Даны четыре элемента с ЭДС = 1,5 B и внутренним сопротивлением r = 0,2 Ом. Как нужно соединить эти элементы, чтобы получить от собранной батареи наибольшую силу тока во внешней цепи, имеющей сопротивление R = 0,2 Ом? Определите максимальную силу тока.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
=(67-10)/(4-1)=57/3=19 м/с^2
2)
at = εR
=7,5/(3*√(1+9*1))=0,79 м=79 см
=(3*0,2*0,5*9,8)/(0,5+4*0,2)=2,94/1,3=2,26 Н
=(2*(0,5-2*0,2)*9,8)/(0,5+4*0,2)=1,96/1,3=1,508
=(0,5-2*0,2*9,8)/(0,5+4*0,2)=0,98/1,3=0,75 м/с2
=((10+0,5*10000)*0,833)/(10*0,5)=4173,33/5=
2A = Br r = =(2*6 * 10-6)/(3 * 10-4)= =0,04 м= 4 см
F = - = 
=(2*3,14/60)*(4-2)=0,21 рад/с2 
)=
= 3 * 108 кг * м3
3 g = 
U = 
T2 = 
=√(6*3,14)/(3 * 108*6,67*10−11)=2,7 ч 
, T – время.
=0,2*√(9,81^2+9.81^2)=2,77 Н
=arctg(9,81/9,81)=arctg1=45
I
ᵑrU
= 
=
, ᵑ - динамическая вязкость.
=(1,67 * 10-27*(3×108)^2)/(1,6 * 10-19)*
y = 
Q = =(3,14*50)/(0,69)=227
U = 
=√((5+2)/5)*(480/1,73)=328 м/с
П = -m0gh
=p0*2,8^(-29 *10-3*9,81*
t2 – t1
=(5*1,38*10−23/3*3,14*(3,6 *10-10)^2)*
Q1 = 
p1V2 = 
=0,002-0,001=0,001
=((5+2)/2)*106*0,001=3,5 кДж
Q2 = 
=106 V1 = 
=5/2*0,001*106= 2,5 кДж 
= T3 
=((600-300)-300*ln(600/300))/(600-300)=0,307=30,7 %
E1 = 
=2*118=236 пФ
, D*4πr2 = r3 , 
=
E1 = j1
=(4*0,6)/(3,14*0,0004^2)*5,5 * 10-8*(1+0,0045*2200)=45, 8 В/м
=(0,6*5,5 * 10-8)/6=1,7 мВ/м
, Е-напряженность.
, 
, 
n= 2, m = 2