5 вар вышка. 5 вар. Решение Сначала построим график функции и определим интервалы нахождении корней уравнения

• Название: Решение Сначала построим график функции и определим интервалы нахождении корней уравнения
• Анкор: 5 вар вышка
• Дата: 10.05.2023
• Размер: 286.82 Kb.
• Имя файла: 5 вар.docx
• Тип: Решение; #1119499
• страница: 2 из 6

5. Применяя методы Эйлера и Рунге–Кутта решить уравнения (а), (б) (число шагов для каждого уравнения n = 15).

а)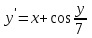







<sub>Решение:

Метод Эйлера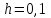:</sub>



Т.к. и , то:



- отрезок.

Оформим в таблице:

i	xi	yi	y'
0	0,6	0,5	1,597450064
1	0,7	0,659745006	1,695561823
2	0,8	0,829301189	1,792990445
3	0,9	1,008600233	1,889637595
4	1	1,197563993	1,985401378
5	1,1	1,39610413	2,080176996
6	1,2	1,60412183	2,173857493
7	1,3	1,821507579	2,266334589
8	1,4	2,048141038	2,357499591
9	1,5	2,283890997	2,447244394
10	1,6	2,528615437	2,535462544
11	1,7	2,782161691	2,622050369
12	1,8	3,044366728	2,706908163
13	1,9	3,315057544	2,789941405
14	2	3,594051685	2,871062004
15	2,1	3,881157885