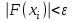5 вар вышка. 5 вар. Решение Сначала построим график функции и определим интервалы нахождении корней уравнения
 Скачать 286.82 Kb. Скачать 286.82 Kb.
|
|
а) 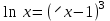 Решение: 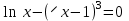 Сначала построим график функции и определим интервалы нахождении корней уравнения: 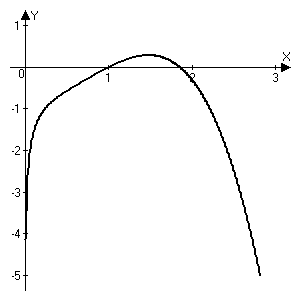 Один корень уравнения равен 1, это видно сразу. Второй корень находится в промежутке от 1 до 2, определим его методом Ньютона. Уточнение значения корня методом Ньютона производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [a; b], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие 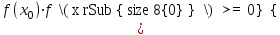 ). В точке ). В точке 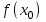 строится касательная к кривой строится касательная к кривой 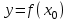 и ищется точка ее пересечения с осью x, которая принимается за новую итерацию. и ищется точка ее пересечения с осью x, которая принимается за новую итерацию.Итерационная формула имеет вид: 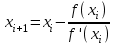 . .Итерационный процесс продолжается до тех пор, пока не будет выполнено условие 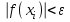 , где , где 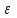 - заданная точность, возьмем 0,001. - заданная точность, возьмем 0,001.Найдем первую и вторую производную функции f(x). 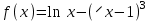 , ,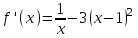 , ,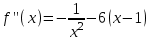 . .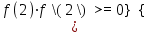 Следовательно, в качестве начального приближения выбираем точку 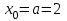 . .Итерационная формула: 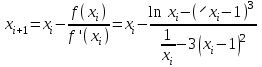 . .Получаем следующее решение (таблица 1). Таблица 1 – Реализация метода Ньютона
Алгоритм остановлен на 4-й итерации при 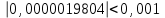 . .Уточненное значение второго корня: 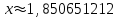 б) 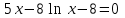 Сначала построим график функции и определим интервалы нахождении корней уравнения: 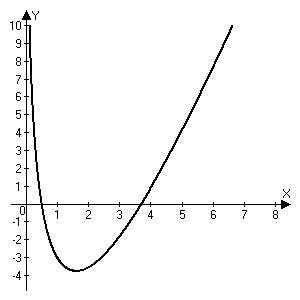 Уравнение имеет 2 корня. Один в промежутке (0, 1), второй (3,4) Так же определим их методом Ньютона. Найдем первую и вторую производную функции f(x). 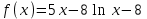 , ,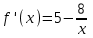 , ,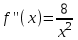 . .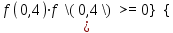 Следовательно, в качестве начального приближения выбираем точку 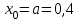 . .Итерационная формула: 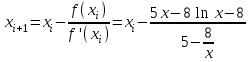 . .Получаем следующее решение (таблица 2). Таблица 2 – Реализация метода Ньютона
Алгоритм остановлен на 3-й итерации при 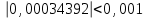 . .Уточненное значение первого корня:  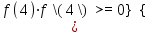 Следовательно, в качестве начального приближения выбираем точку 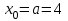 . .Итерационная формула: 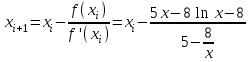 . .Получаем следующее решение (таблица 3). Таблица 3 – Реализация метода Ньютона
Алгоритм остановлен на 3-й итерации при 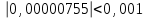 . .Уточненное значение второго корня: 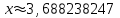 Решить систему линейных уравнений численными методами Решить данную систему 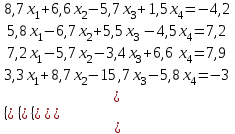 Решение: Решаем методом Гаусса. В методе Гаусса с выбором главного элемента с выбором главного элемента на каждом шаге исключения i-го неизвестного в качестве ведущего используется уравнение (с i-го по n-ое), содержащее максимальный по модулю коэффициент – главный элемент. При этом в качестве него может использоваться один из коэффициентов i-го столбца Для исходной системы выполним сначала прямой ход: 1-й шаг: Наибольший элемент по модулю 1-го столбца 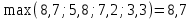 в 1-й строке. в 1-й строке. 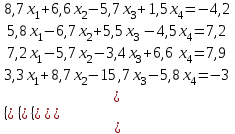 Нормируем первое уравнение и исключаем элементы первого столбца 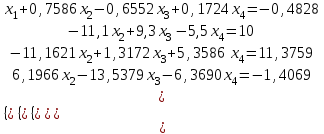 2-й шаг: Наибольший элемент по модулю 2-го столбца 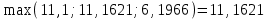 в 3-й строке. Меняем местами 2-е и 3-е уравнение: в 3-й строке. Меняем местами 2-е и 3-е уравнение: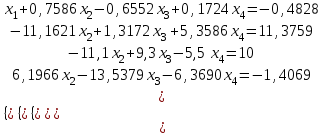 Нормируем второе уравнение и исключаем элементы второго столбца 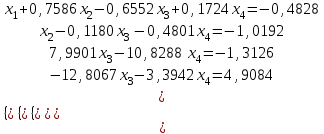 3-й шаг: Наибольший элемент по модулю 3-го столбца 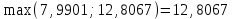 в 4-й строке. Меняем местами 2-е и 3-е уравнение: в 4-й строке. Меняем местами 2-е и 3-е уравнение: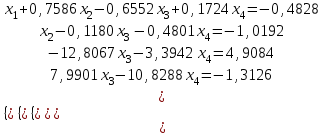 Нормируем третье уравнение и исключаем элементы третьего столбца 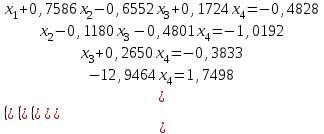 4-й шаг: Нормируем четвертое уравнение: 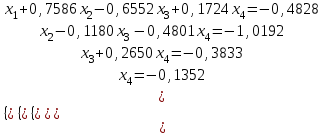 Теперь выполняем обратный ход: 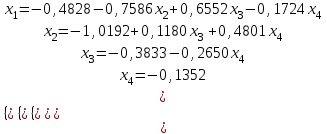 Ответ: (0,1663; -1,1251; -0,3474; -0,1352) 3. Построить интерполяционный многочлен Лагранжа для выбранной функций в заданном интервале (табличные значения: 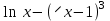 Решение: Выберем узлы:
Решение: Полином ищем в виде: 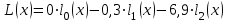 Запишем базисные полиномы Лагранжа: 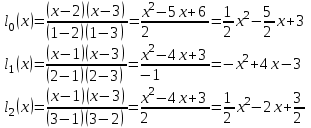 Подставляем базисные полиномы Лагранжа в формулу интерполяционного полинома и суммируем члены с одинаковыми степенными показателями: 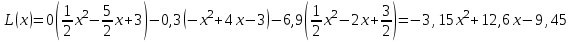 4. Вычислить определенные интегралы с использованием квадратурных формул: а) 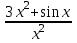 , , 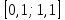 Решение: Примем 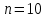 Формула метода Симпсона имеет вид: 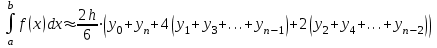 . . Шаг: 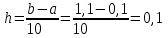 . .Для удобства представим результаты в виде таблицы
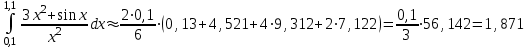 б) 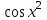 , , 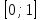 Решение: Примем 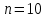 Формула метода трапеций имеет вид: 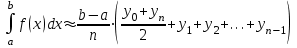 . . Шаг: 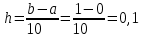 . .Для удобства представим результаты в виде таблицы
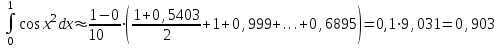 |