5 вар вышка. 5 вар. Решение Сначала построим график функции и определим интервалы нахождении корней уравнения
 Скачать 286.82 Kb.
|
|
6. Найти минимум заданной целевой функции в заданном интервале с заданной точностью:  в интервале [0, 10], = 0,1.Решение: Используем для этого Метод золотого сечения. Положим: a1 = a, b1 = b. Вычислим: λ1 = a1 + (1 – 0,618)*(b1 – a1) = 3,82, μ1 = a1 + 0,618*(b1 – a1) = 6,18. Вычислим: f(λ1) = 1476,0303, f(μ1) = 196505327,9042 Поскольку: f(λ1) < f(μ1), то b2 = 6,18, a2 = a1, μ2 = 3,82, f(μ2) =196505327,9042 λ2 = a2 + (1 – 0,618)*(b2 – a2) = 0 + (1 – 0,618)*(6,18 – 0) = 3,82, f(3,82) = 1476,0303 Поскольку f(λ2) < f(μ2), то b3 = 3,82, a3 = a2, μ3 = 2,3608, f(μ3) =1476,0303 λ3 = a3 + (1 – 0,618)*(b3 – a3) = 0 + (1 – 0,618)*(3,82 – 0) = 2,3608, f(2,3608) = 17,0429 Поскольку f(λ3) < f(μ3), то b4 = 2,3608, a4 = a3, μ4 = 1,4592, f(μ4) = 17,0429 λ4 = a4 + (1 – 0,618)*(b4 – a4) = 0 + (1 – 0,618)*(2.3608 – 0) = 1,4592, f(1,4592) = 7,6478 Поскольку f(λ4) > f(μ4), то a5 = 0,9018, b5 = b4, λ5 = 1,4592, f(λ5) = 10,3065 μ5 = a5 + 0,618*(b5 – a5) = 0,9018 + 0,618*(2,3608 – 0,9018) = 1,8034, f(1,8034) = 7,6478 Остальные расчеты сведем в таблицу:
|7,5179 – 7,5167| ≤ 0,1 Находим x как середину интервала [a, b]: x = (1,6217 + 1,5405)/2 = 1,5811183883908 Ответ: x = 1,5811183883908; F(x) = 7,5167 7. Найти минимум многомерной целевой функции с заданной точностью:  ,  Решение: Вычислим значение функции в начальной точке: 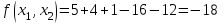 В качестве направления поиска выберем вектор градиент в текущей точке: 
Значение градиента в точке X0:  Проверим критерий остановки:  Имеем:  Сделаем шаг вдоль ньютоновского направления:  Найдем матрицу Гессе и обратный гессиан:  Матрица Гессе: 
Обратный гессиан:  Получим: 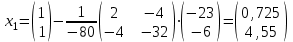  В этой точке  и матрица Гессе положительно определена, следовательно,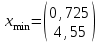 
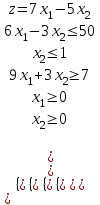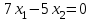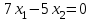8. Решить стандартную задачу линейного программирования:  Решение: Найдем максимум функции. Решим задачу графически. Строим область ограничения функции и целевую функцию.  Прямую  будем двигать параллельно до последнего касания с нашей областью ограничения. В точке, в которой прямая в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.Функция z достигает наибольшего значения в точке A. Координаты точки A (25/3,0). Вычислим значение функции z в точке A (25/3,0):  Найдем минимум функции. Решим задачу графически. Строим область ограничения функции и целевую функцию.  Прямую 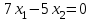будем двигать параллельно до первого касания с нашей областью ограничения. 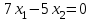В точке, в которой прямая в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.Функция z достигает наименьшего значения в точке A. Координаты точки A (4/9,1). Вычислим значение функции z в точке A (4/9,1):  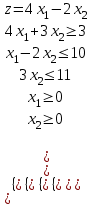 Решение: Найдем максимум функции. Решим задачу графически. Строим область ограничения функции и целевую функцию. 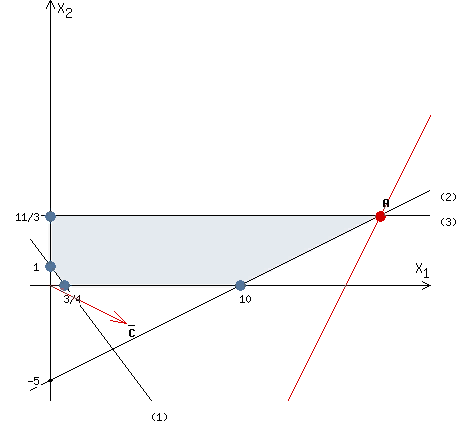 Прямую 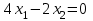 будем двигать параллельно до последнего касания с нашей областью ограничения. 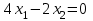В точке, в которой прямая в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.Функция z достигает наибольшего значения в точке A. Координаты точки A (52/3, 11/3). Вычислим значение функции z в точке A (52/3, 11/3):  Найдем минимум функции. Решим задачу графически. Строим область ограничения функции и целевую функцию.  Прямую 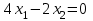будем двигать параллельно до первого касания с нашей областью ограничения. 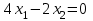В точке, в которой прямая в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.Функция z достигает наименьшего значения в точке A. Координаты точки A (0,11/3). Вычислим значение функции z в точке A (0,11/3):   Решение: Найдем максимум функции. Решим задачу графически. Строим область ограничения функции и целевую функцию.  Прямую  будем двигать параллельно до последнего касания с нашей областью ограничения. В точке, в которой прямая в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.Координаты точки A (7,0) Вычислим значение функции F в точке A (7,0): z(A) = 1 * 7 + 1 * 0 = 7 Найдем координаты точки B:  Вычислим значение функции F в точке B (9/4,19/4): z(B) = 1 * 9/4 + 1 * 19/4 = 7 F(A) = F(B) Значит, функция F достигает своего наибольшего значения в любой точке отрезка AB. Найдем минимум функции. Решим задачу графически. Строим область ограничения функции и целевую функцию.  Прямую будем двигать параллельно до первого касания с нашей областью ограничения. В точке, в которой прямая в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.Функция z достигает наименьшего значения в точке A. Координаты точки A (2/3, 0). Вычислим значение функции z в точке A (2/3, 0):   Решение: Находим максимум функции, решаем Симплекс-методом: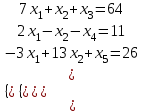 
|