зпр. Решением федерального учебнометодического объединения по общему образованию (протокол от 18 марта 2022 г. 122)
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
|
Место учебного курса в учебном плане Согласно учебному плану в 7–9 классах изучается учебный курс «Алгебра», который включает следующие основные разделы содержания: «Числа и вычисления», «Алгебраические выражения», «Уравнения и неравенства», «Функции». Учебный план на изучение алгебры в 7–9 классах отводит не менее 3 учебных часов в неделю в течение каждого года обучения, всего за три года обучения – не менее 306 учебных часов. Содержание учебного курса (по годам обучения) 7 класс Числа и вычисления Рациональные числа Дроби обыкновенные и десятичные, переход от одной формы записи дробей к другой. Понятие рационального числа, запись, сравнение, упорядочивание рациональных чисел. Арифметические действия с рациональными числами. Решение задач из реальной практики на части, на дроби. Степень с натуральным показателем: определение, преобразование выражений на основе определения, запись больших чисел. Проценты, запись процентов в виде дроби и дроби в виде процентов. Три основные задачи на проценты, решение задач из реальной практики. Применение признаков делимости, разложение на множители натуральных чисел. Реальные зависимости, в том числе прямая и обратная пропорциональности. Алгебраические выражения Переменные, числовое значение выражения с переменной. Допустимые значения переменных. Представление зависимости между величинами в виде формулы. Вычисления по формулам. Преобразование буквенных выражений, тождественно равные выражения, правила преобразования сумм и произведений, правила раскрытия скобок и приведения подобных слагаемых. Свойства степени с натуральным показателем. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Разложение многочленов на множители. Уравнения Уравнение, корень уравнения, правила преобразования уравнения, равносильность уравнений. Линейное уравнение с одной переменной, число корней линейного уравнения, решение линейных уравнений. Составление уравнений по условию задачи. Решение текстовых задач с помощью уравнений. Линейное уравнение с двумя переменными и его график14. Система двух линейных уравнений с двумя переменными. Решение систем уравнений способом подстановки. Примеры решения текстовых задач с помощью систем уравнений. Координаты и графики. Функции Координата точки на прямой. Числовые промежутки. Расстояние между двумя точками координатной прямой. Прямоугольная система координат, оси Ox и Oy. Абсцисса и ордината точки на координатной плоскости. Примеры графиков, заданных формулами. Чтение графиков реальных зависимостей. Понятие функции. График функции. Свойства функций. Линейная функция, её график. График функции y = kx + b. Графическое решение линейных уравнений и систем линейных уравнений. 8 КЛАСС Числа и вычисления Квадратный корень из числа. Понятие об иррациональном числе. Десятичные приближения иррациональных чисел. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям. Действительные числа. Степень с целым показателем и её свойства. Стандартная запись числа. Алгебраические выражения Квадратный трёхчлен; разложение квадратного трёхчлена на множители. Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Рациональные выражения и их преобразование. Уравнения и неравенства Квадратное уравнение, формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Простейшие дробно-рациональные уравнения. Графическаяинтерпретацияуравненийсдвумяпеременными и систем линейных уравнений с двумя переменными. Примеры решения систем нелинейных уравнений с двумя переменными. Решение текстовых задач алгебраическим способом. Числовые неравенства и их свойства. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Системы линейных неравенств с одной переменной. Функции Понятие функции. Область определения и множество значений функции. Способы задания функций. График функции. Чтение свойств функции по её графику. Примеры графиков функций, отражающих реальные процессы. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики. Функции y = x2, y = x3, y = 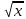 , y = , y = 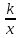 . Графическое решение уравнений и систем уравнений. . Графическое решение уравнений и систем уравнений.9 КЛАСС Числа и вычисления Действительные числа Рациональные числа, иррациональные числа, конечные и бесконечные десятичные дроби. Множество действительных чисел; действительные числа как бесконечные десятичные дроби. Взаимно однозначное соответствие между множеством действительных чисел и координатной прямой. Сравнение действительных чисел, арифметические действия с действительными числами. Измерения, приближения, оценки Размеры объектов окружающего мира, длительность процессов в окружающем мире. Приближённое значение величины, точность приближения. Округление чисел. Прикидка и оценка результатов вычислений. Уравнения и неравенства Уравнения с одной переменной Линейное уравнение. Решение уравнений, сводящихся к линейным. Квадратное уравнение. Решение уравнений, сводящихся к квадратным. Биквадратное уравнение. Примеры решения уравнений третьей и четвёртой степеней разложением на множители. Решение дробно-рациональных уравнений. Решение текстовых задач алгебраическим методом. Системы уравнений Уравнение с двумя переменными и его график. Решение систем двух линейных уравнений с двумя переменными. Решение систем двух уравнений, одно из которых линейное, а другое — второй степени. Графическая интерпретация системы уравнений с двумя переменными. Решение текстовых задач алгебраическим способом. Неравенства Числовые неравенства и их свойства. Решение линейных неравенств с одной переменной. Решение систем линейных неравенств с одной переменной. Квадратные неравенства. Графическая интерпретация неравенств и систем неравенств с двумя переменными. Функции Квадратичная функция, её график и свойства. Парабола, координаты вершины параболы, ось симметрии параболы. Графики функций: y = kx, y = kx + b, y = x2, y = 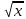 , y = , y = 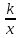 и их свойства. и их свойства.Числовые последовательности Определение и способы задания числовых последовательностей Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых n членов. Изображение членов арифметической и геометрической прогрессий точками на координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты. Примерная рабочая программа учебного курса «Геометрия». 7–9 классы Цели изучения учебного курса Общие цели изучения учебного курса «Геометрия» представлены в ПООП ООО. Они заключаются, прежде всего в том, что на уроках геометрии обучающийся учится проводить доказательные рассуждения, строить логические умозаключения, доказывать истинные утверждения и строить контрпримеры к ложным, проводить рассуждения «от противного», отличать свойства от признаков, формулировать обратные утверждения. В обучении умению рассуждать состоит важное воспитательное значение изучения геометрии, присущее именно отечественной математической школе. Второй целью изучения геометрии является использование её как инструмента при решении как математических, так и практических задач, встречающихся в реальной жизни. Этому соответствует вторая, вычислительная линия в изучении геометрии в школе. Для этого учителю рекомендуется подбирать задачи практического характера для рассматриваемых тем, учить обучающихся строить математические модели реальных жизненных ситуаций, проводить вычисления и оценивать адекватность полученного результата. Крайне важно подчёркивать связи геометрии с другими предметами, мотивировать использовать определения геометрических фигур и понятий, демонстрировать применение полученных умений в физике и технике. Эти связи наиболее ярко видны в темах «Векторы», «Тригонометрические соотношения», «Метод координат» и «Теорема Пифагора». Место учебного курса в учебном плане Согласно учебному плану в 7–9 классах изучается учебный курс «Геометрия», который включает следующие основные разделы содержания: «Геометрические фигуры и их свойства», «Измерение геометрических величин», а также «Декартовы координаты на плоскости», «Векторы», «Движения плоскости» и «Преобразования подобия». Учебный план предусматривает изучение геометрии на базовом уровне, исходя из не менее 68 учебных часов в учебном году, всего за три года обучения – не менее 204 часов. Содержание учебного курса (по годам обучения) 7 класс Начальные понятия геометрии. Точка, прямая, отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла. Ломаная, многоугольник. Параллельность и перпендикулярность прямых. Симметричные фигуры. Основные свойства осевой симметрии15. Примеры симметрии в окружающем мире. Основные построения с помощью циркуля и линейки. Треугольник. Высота, медиана, биссектриса, их свойства. Равнобедренный и равносторонний треугольники. Неравенство треугольника. Свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Свойства и признаки параллельных прямых. Сумма углов треугольника. Внешние углы треугольника. Прямоугольный треугольник. Свойство медианы прямоугольного треугольника, проведённой к гипотенузе. Признаки равенства прямоугольных треугольников. Прямоугольный треугольник с углом в 30о. Неравенства в геометрии: неравенство треугольника, неравенство о длине ломаной, теорема о большем угле и большей стороне треугольника. Перпендикуляр и наклонная. Геометрическое место точек. Биссектриса угла и серединный перпендикуляр к отрезку как геометрические места точек. Окружность и круг, хорда и диаметр, их свойства. Взаимное расположение окружности и прямой. Касательная и секущая к окружности. Окружность, вписанная в угол. Вписанная и описанная окружности треугольника. 8 класс Четырёхугольники. Параллелограмм, его признаки и свойства. Частные случаи параллелограммов (прямоугольник, ромб, квадрат), их признаки и свойства. Трапеция, равнобокая трапеция, её свойства и признаки. Прямоугольная трапеция. Метод удвоения медианы. Центральная симметрия. Теорема Фалеса и теорема о пропорциональных отрезках. Средние линии треугольника и трапеции. Центр масс треугольника. Подобие треугольников, коэффициент подобия. Признаки подобия треугольников. Применение подобия при решении практических задач. Свойства площадей геометрических фигур. Формулы для площади треугольника, параллелограмма, ромба и трапеции. Отношение площадей подобных фигур. Вычисление площадей треугольников и многоугольников на клетчатой бумаге. Теорема Пифагора. Применение теоремы Пифагора при решении практических задач. Синус, косинус, тангенс острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Тригонометрические функции углов в 30о, 45о и 60о. Вписанные и центральные углы, угол между касательной и хордой. Углы между хордами и секущими. Вписанные и описанные четырёхугольники. Взаимное расположение двух окружностей. Касание окружностей. Общие касательные к двум окружностям. 9 класс Синус, косинус, тангенс углов от 0о до 180о. Основное тригонометрическое тождество. Формулы приведения. Решение треугольников. Теорема косинусов и теорема синусов. Решение практических задач с использованием теоремы косинусов и теоремы синусов. Преобразование подобия. Подобие соответственных элементов. Теорема о произведении отрезков хорд, теоремы о произведении отрезков секущих, теорема о квадрате касательной. Вектор, длина (модуль) вектора, сонаправленные векторы, противоположно направленные векторы, коллинеарность векторов, равенство векторов, операции над векторами. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Скалярное произведение векторов, применение для нахождения длин и углов. Декартовы координаты на плоскости. Уравнения прямой и окружности в координатах, пересечение окружностей и прямых. Метод координат и его применение. Правильные многоугольники. Длина окружности. Градусная и радианная мера угла, вычисление длин дуг окружностей. Площадь круга, сектора, сегмента. Движения плоскости и внутренние симметрии фигур (элементарные представления). Параллельный перенос. Поворот. Примерная рабочая программа учебного курса «Вероятность и статистика» 7–9 классы Цели изучения учебного курса В современном цифровом мире вероятность и статистика приобретают всё большую значимость, как с точки зрения практических приложений, так и их роли в образовании. Каждый человек постоянно принимает решения на основе имеющихся у него данных. А для обоснованного принятия решения в условиях недостатка или избытка информации необходимо в том числе хорошо сформированное вероятностное и статистическое мышление. Именно поэтому остро встала необходимость сформировать у обучающихся, в том числе обучающихся с ЗПР, функциональную грамотность, включающую в себя в качестве неотъемлемой составляющей умение воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных процессов и зависимостей, производить простейшие вероятностные расчёты. Знакомство с основными принципами сбора, анализа и представления данных из различных сфер жизни общества и государства приобщает обучающихся к общественным интересам. В структуре программы учебного курса «Вероятность и статистика» основной школы выделены следующие содержательно-методические линии: «Представление данных и описательная статистика»; «Вероятность»; «Элементы комбинаторики»; «Введение в теорию графов». Содержание линии «Представление данных и описательная статистика» служит основой для формирования навыков работы с информацией: от чтения и интерпретации информации, представленной в таблицах, на диаграммах и графиках до сбора, представления и анализа данных с использованием статистических характеристик средних и рассеивания. Работая с данными, обучающиеся с ЗПР учатся считывать и интерпретировать данные, выдвигать, аргументировать и критиковать простейшие гипотезы, размышлять над факторами, вызывающими изменчивость, и оценивать их влияние на рассматриваемые величины и процессы. Интуитивное представление о случайной изменчивости, исследование закономерностей и тенденций становится мотивирующей основой для изучения теории вероятностей. Большое значение для обучающихся с ЗПР здесь имеют практические задания, в частности опыты с классическими вероятностными моделями. Понятие вероятности вводится как мера правдоподобия случайного события. При изучении курса обучающиеся с ЗПР знакомятся с простейшими методами вычисления вероятностей в случайных экспериментах с равновозможными элементарными исходами, вероятностными законами, позволяющими ставить и решать более сложные задачи. В курс входят начальные представления о случайных величинах и их числовых характеристиках. Также в рамках этого курса осуществляется знакомство обучающихся с ЗПР с множествами и основными операциями над множествами, рассматриваются примеры применения для решения задач, а также использования в других математических курсах и учебных предметах. Место учебного курса в учебном плане В 7–9 классах изучается курс «Вероятность и статистика», в который входят разделы: «Представление данных и описательная статистика»; «Вероятность»; «Элементы комбинаторики»; «Введение в теорию графов». На изучение данного курса отводит 1 учебный час в неделю в течение каждого года обучения, всего 102 учебных часа. Содержание учебного курса (по годам обучения) |
