Руководство к лабораторным работам по медицинской и биологической физике. Руководство к лабораторным работам по медицинской и биологическо. Руководство к лабораторным работам по медицинской и биологической физике красноярск 2004

• Название: Руководство к лабораторным работам по медицинской и биологической физике красноярск 2004
• Анкор: Руководство к лабораторным работам по медицинской и биологической физике.doc
• Дата: 30.01.2017
• Размер: 10.98 Mb.
• Имя файла: Руководство к лабораторным работам по медицинской и биологическо.doc
• Тип: Руководство; #1280
• Категория: Физика
• страница: 4 из 24

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Способность реальных жидкостей оказывать сопротивление движению в них тел или собственному течению за счет сил межмолекулярного взаимодействия называется внутренним трением или вязкостью жидкости. Это явление наиболее наглядно в случае течения жидкости между двумя твердыми пластинами, когда верхняя пластина равномерно движется параллельно нижней неподвижной пластине (рис. 1).

Р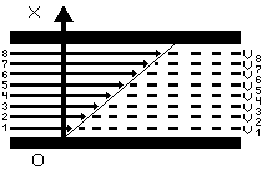
ис. 1. Диаграмма скоростей слоев жидкости, подчиняющейся формуле Ньютона.

Благодаря межмолекулярному взаимодействию верхний слой жидкости будет иметь скорость, равную скорости верхней пластины υ_в , а самый нижний слой будет неподвижным (υ=0). Промежуточные слои за счет силы внутреннего трения (между ними) будут иметь промежуточные значения скорости (0< υ < υ_в). Если изменение скорости слоев с расстоянием линейно, то величина силы внутреннего трения F_тр определяется уравнением Ньютона:

, (1)

где  - коэффициент внутреннего трения или динамическая вязкость (зависит от природы вещества и условий измерений), - градиент скорости (характеризует изменение скорости между слоями с расстоянием в направлении перпендикулярном скорости), S - площадь соприкосновения слоев.

Графически это течение жидкости представлено на рис. 1. Такие жидкости называют ньютоновскими. Коэффициент вязкости таких cред зависит от их природы, температуры (с повышением температуры он понижается), и от давления при низких температурах. К ньютоновским жидкостям относятся вода, низкомолекулярные органические соединения, истинные расплавы металлов и их солей.

Если жидкость имеет сложное строение и содержит крупные молекулы (например, растворы полимеров, белков), то они обладают повышенной вязкостью, так как, кроме преодоления отмеченной силы межмолекулярного взаимодействия, работа внешних сил затрачивается также на разрушение создаваемых группами молекул пространственных структур. Течение таких жидкостей не подчиняется формуле Ньютона, а жидкости называются неньютоновскими или структурно вязкими.

В частности, кровь, представляющая собой суспензию форменных элементов в белковом растворе - плазме, относится к неньютоновским жидкостям. Однако в ряде случаев коэффициент вязкости крови принимают за постоянную величину, получая его приближенные значения.

Часто при изучении вязкости жидкости определяют кривую течения - зависимость напряжения сдвига =F/S от градиента скорости (рис. 2).

Для ньютоновской жидкости (1) график начинается из начала координат и возрастает линейно с увеличением градиента скорости. Действительно, согласно формуле (1):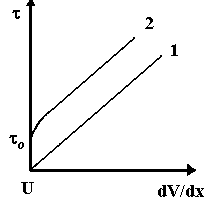

. (2)


Рис. 2. Зависимость напряжения сдвига  от градиента скорости для ньютоновской (1) и неньютоновской (2) жидкостей.
Следовательно, показатель динамической вязкости ньютоновской жидкости - константа и не зависит от градиента скорости.

Для неньютоновской жидкости (2) график начинается от некоторого значения ₀ (предельное напряжение сдвига) и возрастает нелинейно с увеличением градиента скорости. То есть показатель динамической вязкости  неньютоновской жидкости зависит от градиента скорости. У таких жидкостей коэффициент вязкости зависит также от режима течения и давления. Их вязкость характеризуют так называемым условным коэффициентом вязкости, зависящим от условий течения жидкости.

Коэффициент внутреннего трения растворов вязких жидкостей за­висит от их концентрации. При увеличении концентрации таких жидкостей вязкость возрастает.

Единица коэффициента вязкости в СИ - (Нс/м² ) ( Пас ) (паскаль ^.секунда), в системе СГС – (динс/см²) (П) (пуаз). Связь между этими величинами 1 Пас = 10 П. На практике часто используют относительную вязкость _отн, определяя отношение коэффициента вязкости исследуемой жидкости к коэффициенту вязкости воды _о. при тех же условиях (при t = 20⁰С и _о 1 сП).

Измерение вязкости имеет важное практическое значение для медицины. Относительная вязкость крови в норме составляет 4,2-6. При патологиях она может снижаться до 2-3 (при анемии) или повышаться до 15-20 (при полицитамии), что отражается на скорости оседания эритроцитов (СОЭ). Вязкость крови различна у мужчин (4,3-5,9) и женщин (3,9-4,9), изменяется с возрастом, что важно при судебно-медицинских исследованиях. Относительная вязкость сыворотки крови - 1,4-1,7, у плазмы - 1,5-1,8. Вязкость крови зависит от концентрации эритроцитов и белков плазмы, а так же от их состава, от размеров клеток крови, эластичности мембран эритроцитов.

Стационарное движение жидкостей является ламинарным. При ламинарном течении различные слои жидкости текут не перемешиваясь, параллельно друг другу. При ламинарном течении жидкости по трубе постоянного сечения скорость движения слоев увеличивается от периферии к центру (рис. 3).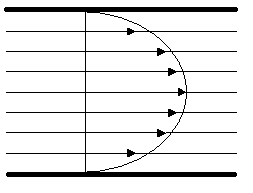



Рис. 3. Ламинарное течение жидкости в трубе.
Максимальная скорость будет вдоль оси трубы, минимальная (практически равная 0) - у пристеночных слоев. Поэтому разность между скоростями двух соседних слоев имеет наибольшее значение у стенок трубы, а минимальное - в центре. Если концы векторов скоростей слоев соединить плавной кривой, то получится парабола.

Увеличение скорости течения вязкой жидкости вследствие неоднородности давления по поперечному сечению трубы создает завихрения, и движение становится вихревым или турбулентным. При турбулентном течении скорости частиц в каждом месте непрерывно и хаотически меняются, движение является нестационарным, сопровождается шумом.

Характер течение жидкости по трубе зависит от ее поверхности, диаметра D, от свойств жидкости (плотности  и вязкости ), ее скорости υ и определяется числом Рейнольдса:

. (3)

Если число Рейнольдса больше некоторого критического, то движение жидкости будет турбулентным. Например, для гладких цилиндрических труб Rе_кр = 2300, а для кровеносных сосудов в норме Rе_кр = 2000.
МЕТОДЫ ИЗМЕРЕНИЯ ВЯЗКОСТИ ЖИДКОСТИ

1. Метод Стокса

Применяют для исследования жидкостей с большой вязкостью. Опытным путем Стокс установил, что при равномерном движении шара в вязкой жидкости сила сопротивления F_тр движению прямо пропорциональна скорости υ, радиусу шара R и коэффициенту вязкости жидкости 

. (4)

Определив скорость движения шарика и зная его размер и плотность ρ, а также плотность жидкости ρ_Ж, находят ее вязкость

. (5)

2. Метод капиллярного вискозиметра

Применяют при изучении жидкостей с невысокой вязкостью. Методика измерения коэффициента вязкости капиллярным вискозиметром основана на измерении скорости течения жидкости в капиллярной трубке (рис. 4).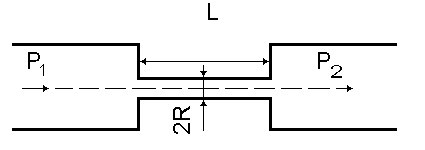



Рис. 4. Течение жидкости по капиллярной трубке.
Скорость протекания жидкости по трубе υ зависит от разности давлений (Р₁-Р₂) на концах трубы, ее длины L, радиуса R и вязкости жидкости:
.
Формула Пуазейля определяет зависимость Q - объема жидкости, протекающей за единицу времени через трубу длиной L, радиусом R, при разности давлений на концах трубы (Р₁< Р₂), от вязкости

. (6)

Величина называется гидравлическим сопротивлением.

Формула Пуазейля справедлива только для ламинарного течения. Поэтому, чтобы при обычных скоростях не возникало турбулентное течение, на практике пользуются капиллярными трубками. А так как точно измерить все входящие в нее величины трудно, то чаще всего определяют относительный коэффициент вязкости, то есть вязкость исследуемой жидкости относительно другой жидкости, чаще всего воды. С этой целью измеряют время протекания какого-то объема V исследуемой жидкости и время t протекания такого же объема воды. Тогда для эталонной жидкости, учитывая, что V = Q t, согласно формуле (6):

, (7)

а для исследуемой жидкости:

, (8)

где ∆P₀ , ∆P_x - разность давлений на концах трубки (капилляра) для эталонной и исследуемой жидкости соответственно; η₀ , η_х – коэффициенты вязкости эталонной и исследуемой жидкости соответственно; t₀, t_x – время протекания эталонной и исследуемой жидкости через капилляр длиной L и радиусом R.

Так как объемы жидкостей в этих условиях одинаковы, то, приравнивая правые части уравнений (7) и (8) и заменив отношение давлений отношением плотностей исследуемых жидкостей, получим уравнение для определения относительной вязкости:

. (9)
3. Ротационный вискозиметр

Применяют для определения вязкости неньютоновских жидкостей. Так как большинство биологических жидкостей являются неньютоновскими, то этот прибор представляет интерес для медико-биологических исследований. Вискозиметр состоит из двух соосно расположенных цилиндров вставленных друг в друга (рис. 5).

Между цилиндрами имеется небольшой зазор, в который помещается исследуемая жидкость. Внешний цилиндр крепят на валу электродвигателя, а внутренний подвешивают на упругом подвесе – спиральной пружине с известными характеристиками. Внешнему цилиндру сообщают заданную угловую скорость ω. За счет вязкости жидкости определенный момент силы М сообщается внутреннему цилиндру, и происходит его поворот вокруг оси на некоторый угол.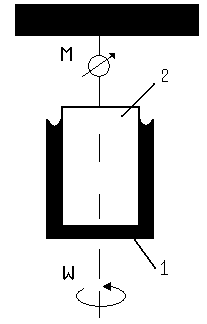


Рис. 5. Схема ротационного вискозиметра (1 – внешний цилиндр, 2 – внутренний).
Чем больше скорость вращения, тем на больший угол повернется внутренний цилиндр. С учетом упругости пружины круговая шкала позволяет измерять вязкость жидкости при различных скоростях вращения, то есть при разных значениях градиента скорости в жидкости между цилиндрами. Обычно определяют "кривую течения" - зависимость касательного напряжения F_тp/S от градиента скорости dυ/dx.