Практическое руководство-ФинМат. Руководство к практическим занятиям и самостоятельной работе по финансовой математике Содержание по финансовой математике 1

• Название: Руководство к практическим занятиям и самостоятельной работе по финансовой математике Содержание по финансовой математике 1
• Дата: 10.02.2018
• Размер: 1.16 Mb.
• Имя файла: Практическое руководство-ФинМат.doc
• Тип: Руководство; #36180
• страница: 4 из 14

Тема 4. Сложные учетные ставки

Дисконтирование по сложной учетной ставке осуществляется в ситуации предварительного начисления сложного процента, т.е. когда сложный процент (например, за кредит) начисляется в момент заключения финансового соглашения. В этом случае в начале каждого периода начисления проценты начисляются не на одну и ту же величину (как при дисконтировании по простой учетной ставке), а каждый раз на новую, полученную в результате дисконтирования, осуществленного в предыдущем периоде.

Для лица, осуществляющего предварительное начисление процентов более выгода сложная учетная ставка, если срок учета менее одного года; более выгодна простая учетная ставка, если срок учета превышает один год.

Если продолжительность финансовой операции не равна целому числу лет, то при определении стоимости учетного капитала используют либо сложную учетную ставку, либо смешанную схему (сложная учетная ставка для целого числа лет и простая учетная ставка для дробной части года). Стоимость учетного капитала больше при использовании смешанной схемы.

Начисления сложных процентов могут быть дискретными и непрерывными. Уменьшая период начисления и увеличивая частоту начисления процентов переходят к так называемому непрерывному проценту, при котором наращенная сумма (при схеме сложных процентов) увеличивается максимально. Формулы для вычисления наращенной суммы при начислении ссудных и учетных процентов совпадают, т.к. при уменьшении периода начисления разница между начислением процентов в начале и в конце периода исчезает. Непрерывную ставку начисления процента обозначают  и называют силой роста.

Цель проведения занятия - научиться проводить расчеты по схеме сложных ссудных процентов, используя формулы финансовых вычислений; провести сравнение финансовых операций при использовании простых и сложных ставок.

Основные формулы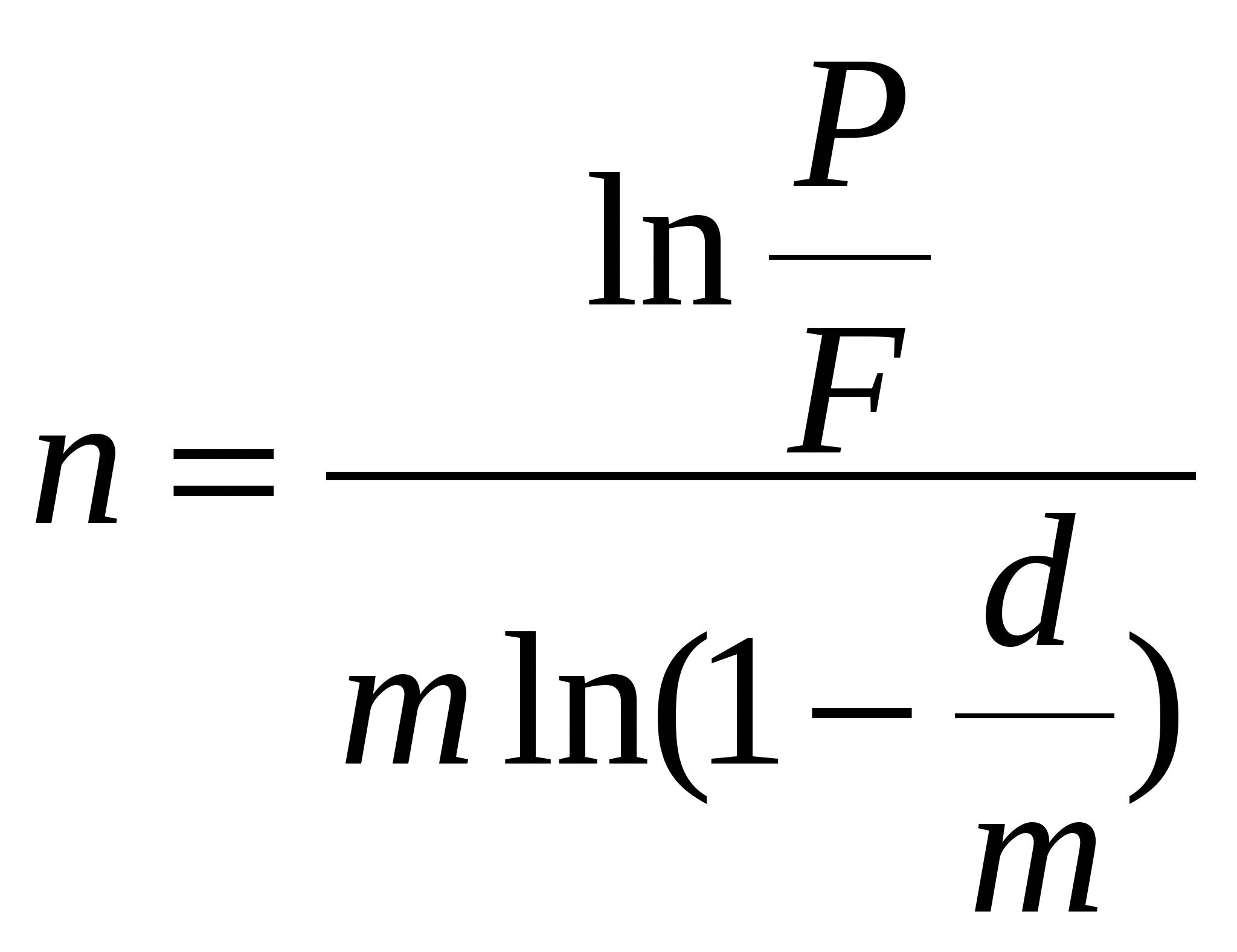

(4.1)

(4.2)

(4.3)

(4.4)

(4.5)

(4.6)

(4.7)

(4.8)

(4.9)

(4.10)

где

F– наращенная сумма;

P- вложенная сумма;

n- количество лет;

d- сложная учетная ставка;

непрерывная ставка

m- количество начислений процентов в году;

w- целая часть периода финансовой операции;

f- дробная часть периода финансовой операции.
Типовые задачи с решениями

Задача 1. Вексель на сумму 70 тыс. руб. со сроком погашения через 4 года учтен за 32 месяца по сложной учетной ставке 24% годовых. Определить суммы, которые получит предъявитель векселя при различных способах учета.

Решение

1) При применении схемы сложных процентов воспользуемся формулой (4.4) при n = 32/12= 8/3, F = 70 тыс. руб., d = 0,24, поэтому.

Владелец векселя получит 33 672 руб.

2) При применении смешанной схемы воспользуемся формулой (4.4) при w = 2, f = 2/3: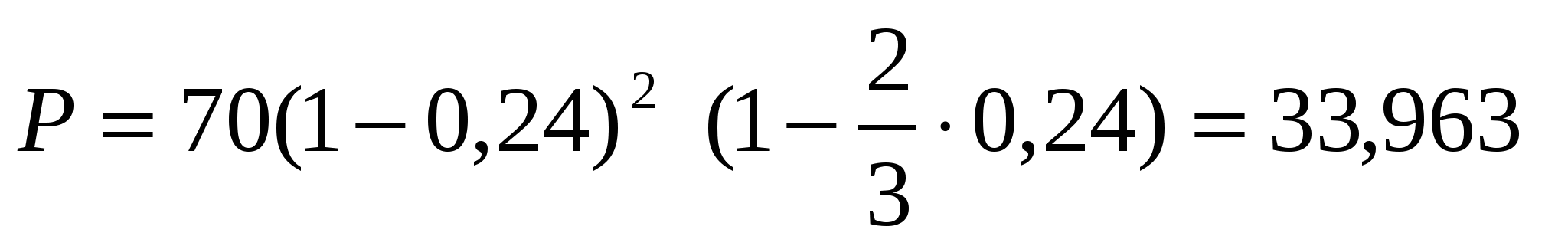

Владелец векселя получит 33 672 руб.

Задача 2. Долговое обязательство на выплату 46 тыс. руб. учтено за 4 года до срока погашения. Определите сумму, полученную при учете этого обязательства, если производилось 1) полугодовое; 2) поквартальное; 1) ежемесячное дисконтирование по сложной учетной ставке 24% годовых.

Решение

1) Используем формулу (4.3) при F = 46; d = 0,24; n = 4; m = 2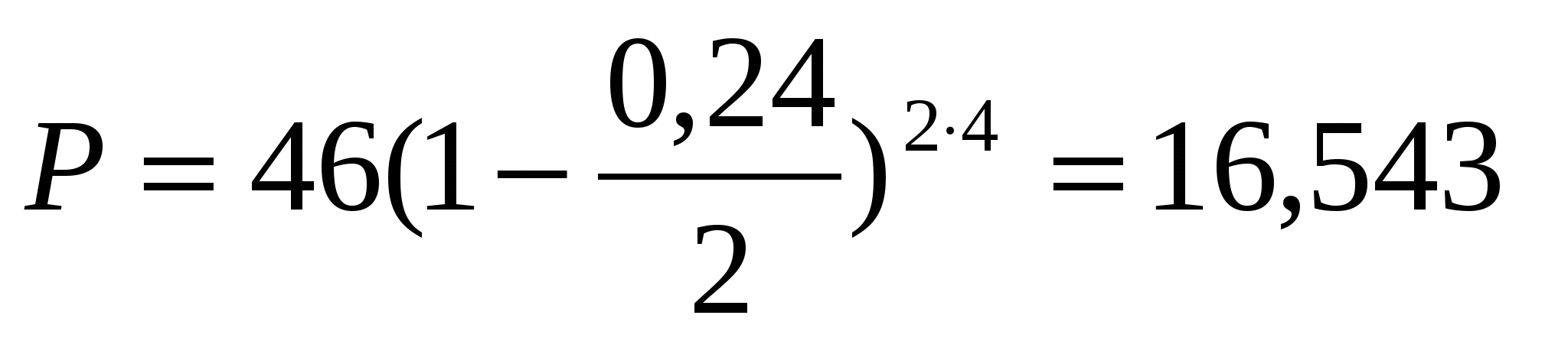



Сумма, полученная при учете обязательства, равна 16 543 руб.

2) Используем формулу (4.3) при F = 46; d = 0,24; n = 4; m = 4:

Сумма, полученная при учете обязательства, равна 17092 руб.

3) Используем формулу (4.3) при F = 46; d = 0,24; n = 4; m = 12:



Сумма, полученная при учете обязательства, равна 17443 руб.

Сравнивая полученные результаты, делаем вывод, что с ростом числа осуществлений операций дисконтирования в году сумма, полученная при учете обязательства, возрастает.

Задача 3. Вексель был учтен за 2,5 года до срока его погашения, при этом владелец векселя получил четверть от написанной на векселе суммы. По какой годовой учетной ставке был учтен этот вексель, если производилось 1) поквартальное дисконтирование; 2) ежемесячное дисконтирование.

Решение

1) по формуле (4.7) при P=0,25F; n=2,5; m=4, получим :



Вексель был учтен по сложной учетной ставке 51,78% годовых.

2) по формуле (4.7) при P=0,25F; n=2,5; m=12, получим :



Вексель был учтен по сложной учетной ставке 54,19 % годовых.

Задача 4. Клиент имеет вексель на 100 тыс. руб., который он хочет учесть 01.03.2010 в банке по сложной учетной ставке равной 7% годовых. Какую сумму он получит, если срок погашения векселя 01.08.2010 г.?

Решение

Срок даты учета до даты погашения векселя равен 153 дня, число дней в году 365. По формуле (4.1) при F=100; d=0,07; n=153/365
=97,038

Владелец векселя получит 97 038 руб.

Задача 5. Вклад в размере 20 тыс. руб. помещен в банк на 5 лет, причем предусмотрен следующий порядок начисления сложных процентов по плавающей годовой учетной ставке : в первые 2 года –16%, в следующие 2 года - 19%, в оставшийся год- 23%. Определить наращенную сумму. При использовании какой постоянной сложной учетной ставки можно получить такую же сумму?

Решение

По формуле (4.6) при d1 = 16%, d2 = 19%, d3 = 23% получаем:



Наращенная сумма равна 56106 руб.

Постоянную годовую учетную ставку d, дающую тот же результат, находим из равенства:



d = 0,1864

Постоянная ставка, которая дает тот же результат, равна 18,64% годовых.
Задачи для самостоятельной подготовки

Задача 1. Вексель на сумму 800 тыс. руб. учитывается за 2 года до срока погашения. Какую сумму получит предъявитель векселя при учете по сложной учетной ставке 20% годовых?

Задача 2. Определите дисконтированную сумму при учете 100 тыс. руб. по простой и сложной учетной ставкам, если годовая ставка равна 18% годовых и учет происходит за 30 дней, 180 дней, 1 год, 3 года, 5 лет. Полагать год равным 360 дней.

Задача 3. За долговое обязательство в 80 тыс. руб. банком было выплачено 62 тыс. руб. За какое время до срока погашения было учтено это обязательство, если банком использовалась годовая сложная учетная ставка 28% годовых ?

Задача 4. Найдите величину дисконта, если долговое обязательство на выплату 4 млн. руб. учтено за 3 года до срока погашения по сложной учетной ставке 1) 20% годовых; 2) 25% годовых.

Задача 5. Долговое обязательство было учтено по номинальной учетной ставке 32% годовых при полугодовом дисконтировании. За какое время до срока погашения было учтено обязательство, если его дисконтированная сумма составила треть от суммы, которую нужно выплатить по этому обязательству?

Задача 6. Согласно финансовому соглашению банк начисляет по полугодиям проценты на вклады по сложной учетной ставке 28% годовых. Определить в виде простой учетной ставки стоимость привлеченных средств для банка при их размещении 1) на 3 месяца; 2) на год.
Контрольные вопросы

1. 
   Чему равен множитель дисконтирования при дисконтировании по сложной учетной ставке?
   
2. 
   Может ли учет по сложной учетной ставке привести к отрицательным значениям?
   
3. 
   Что происходит с величиной учтенного капитала, если растет число осуществлений операций дисконтирования по сложной учетной ставке?