Курсовая. Руководство к выполнению лабораторных работ. Руководство к выполнению лабораторных работ для студентов vi курса
 Скачать 217.43 Kb. Скачать 217.43 Kb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (РУТ (МИИТ)) Кафедра «Тяговый подвижной состав» ТЕОРИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ Руководство к выполнению лабораторных работ для студентов VI курса специальности 23.05.03. Подвижной состав железных дорог М о с к в а - 2022 Лабораторная работа №1 ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ АВТОМАТИКИ Цель работы. Изучение и освоение методики экспериментального определения статических характеристик элементов автоматики Общие положения. 1. При проектировании автоматической системы регулирования должны быть известны статические характеристики и параметры составляющих эту систему функциональных элементов – объекта регулирования, измерительного и усилительно-преобразующих устройств, регулирующего органа и исполнительного механизма. Любой функциональный элемент автоматической системы регулирования имеет входную хвх и выходную хвых координаты. Статическими характеристиками функционального элемента по регулирующему или возмущающему воздействию называются зависимости выходной величины от входной в установившихся режимах при неизменных иных воздействиях (см. рис. 1). По статическим характеристикам функционального элемента можно определить значения коэффициентов передачи (усиления) элемента. Коэффициенты передачи являются статическими параметрами функционального элемента. Коэффициент передачи элемента равен тангенсу угла наклона к оси хвх касательной к статической характеристике, проведенной в данной ее точке. Для нелинейных статических характеристик, изображенных на рис. 1, коэффициент передачи функционального элемента в точке А будет равен kА = 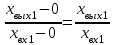 , а в точке В – kВ = , а в точке В – kВ = 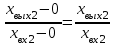 . Участок статической характеристики между точками А и В может быть линеаризован. В этом случае участок нелинейной статической характеристики между точками А и В заменяется отрезком прямой, соединяющей обе эти точки, и тогда коэффициент передачи функционального элемента будет равен kАВ = . Участок статической характеристики между точками А и В может быть линеаризован. В этом случае участок нелинейной статической характеристики между точками А и В заменяется отрезком прямой, соединяющей обе эти точки, и тогда коэффициент передачи функционального элемента будет равен kАВ = 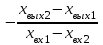 . При таком расположении статических характеристик коэффициенты передачи принимают отрицательные значения. . При таком расположении статических характеристик коэффициенты передачи принимают отрицательные значения.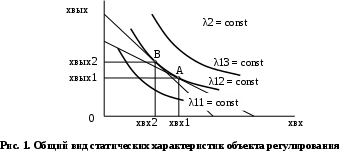 2. Методику экспериментального определения статических характеристик элементов автоматики рассмотрим на примере системы охлаждения тяговой выпрямительной установки как объекта регулирования температуры. Выходной величиной системы охлаждения тяговой выпрямительной установки является температура корпуса диода tд (регулируемая величина φ), входной величиной – объемный расход охлаждающего воздуха Gвз или скорость воздушного потока Vвз (регулирующее воздействие μ), возмущающими воздействиями – нагрузочный ток IВУ (возмущение λ1) и температура охлаждающего воздуха tвз (возмущение λ2). Принципиальная схема лабораторного стенда представлена на рис. 2. В систему охлаждения входят собственно тяговая выпрямительная установка 1, вентилятор 2, воздуховоды, воздушные фильтры. Активно-индуктивная нагрузка (на рис. 2 не показана) тяговой выпрямительной установки на лабораторном стенде имитирует тяговые электродвигатели. Лабораторный стенд оборудован следующими датчиками: датчиком температуры корпуса диода 3, датчиком температуры охлаждающего воздуха 4, датчиком скорости воздушного потока 5, датчиком тока нагрузки тяговой выпрямительной установки 6. Статические характеристики могут быть получены после обработки кривых нагревания корпуса диода tд(τ) при Vвзi = сonst, где τ – текущее время. Так, с кривой нагревания tд(τ) при Vвз1 = сonst, получена точка статической характеристики tд1(Vвз1), соответствующая установившемуся тепловому режиму. При этом Iву = сonst и tвз = сonst. Аналогично получены остальные точки статической характеристики. 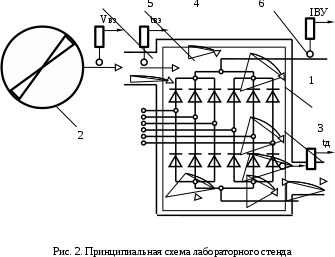 Экспериментальная статическая характеристика объекта регулирования температуры может быть получена также другим путем (см. рис. 3). Устанавливают режим: Vвз1 = сonst, при этом Iву = сonst и tвз = сonst. По окончанию переходного процесса фиксируют значение tд1, затем выставляют Vвз 2 = сonst при Iву = сonst и tвз = сonst и вновь после того, как величина tд примет новое установившееся значение tд2, фиксируют его, и т.д. 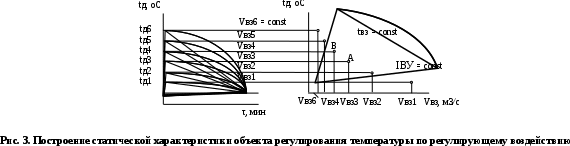 3. Коэффициент передачи объекта регулирования температуры по регулирующему воздействию для участка статической характеристики АВ определяется как kμ = (tд4 - tд3)/(Vвз4 - Vвз3), оС · с/м. (1) Поскольку Vвз4 < Vвз3, то kμ принимает отрицательное значение. Из рис. 3 видно, что статическая характеристика нелинейна, это означает, что коэффициент передачи объекта регулирования температуры есть величина переменная. Последовательность выполнения работы 1. Запустить испытательный стенд 2. Установить режим: Vвз1 = сonst, при этом Iву = сonst и tвз = сonst. По окончанию переходного процесса зафиксировать значение tд1. Выставить Vвз2 = сonst (при тех же Iву = сonst и tвз = сonst) и вновь после того, как величина tд примет новое установившееся значение tд2, зафиксировать его, и т.д. Результаты измерений свести в табл. 1. Таблица 1
3. Пользуясь выражением (1) рассчитать значение коэффициента передачи объекта регулирования температуры по регулирующему воздействию для участков статической характеристики, указанного преподавателем. Результаты расчетов свести в табл. 2. Таблица 2
4. Построить статическую характеристику объекта регулирования температуры. 5. Построить зависимость коэффициента передачи объекта регулирования температуры от регулирующего воздействия kμ(Vвз). Лабораторная работа №2 ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ ЭЛЕМЕНТОВ АВТОМАТИКИ Цель работы. Изучение и освоение методики экспериментального определения динамических характеристик и параметров элементов автоматики Общие положения. Методика экспериментального исследования динамических свойств объекта регулирования базируется на основных положениях классической теории автоматических систем. Методика включает следующие основные положения: 1. Переходные временные характеристики объекта регулирования определяются при однократном скачкообразном изменении только одного из воздействий – регулирующего или одного из возмущающих при поддержании постоянными остальных. 2. Величина однократного скачкообразного воздействия не должна превышать 15% от максимально возможной величины вносимого возмущения. Обычно это воздействие составляет от 5 до 10%. 3. Однократное скачкообразное воздействие вносится при установившемся режиме объекта регулирования. При достижении нового установившегося состояния вносится новое однократное скачкообразное воздействие того же значения, но обратного знака. Полученные по динамическим характеристикам значения динамических параметров усредняют и относят к середине интервала изменения данного воздействия. Исследования динамики объекта регулирования проводятся на том же лабораторном стенде (рис. 2 в лабораторной работе 1). При построении одноконтурных автоматических систем регулирования с П-регулятором, работающим по отклонению измеренного значения регулируемой величины от заданного значения, достаточно определения динамических характеристик и параметров лишь по регулирующему воздействию μ во всем возможном диапазоне изменения возмущающих воздействий λi. Одну и ту же экспериментальную переходную функцию можно аппроксимировать различными видами передаточных функций. Если аппроксимировать экспериментальную переходную функцию решением дифференциального уравнения первого порядка с запаздыванием, то аппроксимирующая передаточная функция запишется в виде 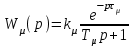 , (1) , (1)где kμ - коэффициент передачи объекта регулирования по регулирующему воздействию, τμ - время запаздывания по регулирующему воздействию, Тμ- постоянная времени объекта по регулирующему воздействию. Решение линейного дифференциального уравнения первого порядка с запаздыванием и нулевыми начальными условиями, соответствующего передаточной функции вида (1), будет иметь вид  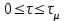  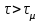 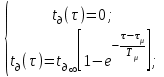  (2) (2) Существуют программы обработки экспериментальных данных, позволяющих эмпирически определять значения динамических параметров элементов автоматики с помощью ПЭВМ. Однако, для приближенного определения значений τμ и Тμможно использовать графический способ (см. рис. 1). В этом случае через точку перегиба экспериментальной кривой (точка А) проводят наклонную прямую, пересекающую ось абсцисс (ось времени) и линию установившегося значения регулируемой величины tд ∞. Отрезок от начала координат до точки пересечения этой прямой оси времени будет соответствовать времени запаздывания τμ. Отрезок между точкой пересечения наклонной прямой оси времени и перпендикуляром, опущенным на ось времени из точки пересечения наклонной прямой линии установившегося значения регулируемой величины tд ∞, соответствует постоянной времени объекта регулирования температуры Тμ. 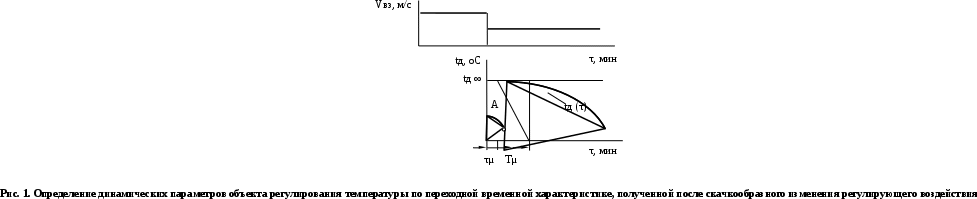 Последовательность выполнения работы 1. Запустить испытательный стенд. 2. Установить режим: Vвз1 = сonst, при этом Iву = сonst и tвз = сonst. По окончанию переходного процесса зафиксировать значение tд1. 3. Изменить режим охлаждения тяговой выпрямительной установки, уменьшив скачком количество охлаждающего воздуха до величины Vвз2при тех же значениях Iву = сonst и tвз = сonst. Через равные промежутки времени фиксировать значения tд до наступления установившегося режима. Результаты измерений свести в табл. 1. Таблица 1
4. Определить значения τμ и Тμ, в соответствии с рис. 1. Лабораторная работа №3 ОПРЕДЕЛЕНИЕ амплитудно-частотных ХАРАКТЕРИСТИК и исследование автоматических систем регулирования на устойчивость Цель работы. Изучение и освоение методики исследования автоматических систем регулирования на устойчивость. Общие положения. В теории автоматических систем широко применяются косвенные методы исследования устойчивости систем регулирования, поскольку непосредственное нахождение корней характеристических уравнений высоких степеней во многих случаях затруднительно. Косвенные методы содержат критерии, с помощью которых можно исследовать устойчивость системы без решения ее характеристического уравнения: критерии И.А.Вышнеградского, Гурвица, А.В.Михайлова, Наквиста-Михайлова и др. Для возможности использования первых трех критериев необходимо располагать уравнением системы. Если же известны экспериментальные характеристики элементов системы, удобней пользоваться амплитудно-фазовым критерием Найквиста-Михайлова, при этом имеется возможность одновременного исследования качества работы системы регулирования. Для построения амплитудно-фазово-частотной характеристики должна быть известна передаточная функция системы регулирования в разомкнутом состоянии. Передаточная функция системы регулирования в разомкнутом состоянии определяется как произведение передаточных функций составляющих систему элементов – объекта регулирования, измерительного и усилительно-преобразующих устройств, исполнительного механизма, регулирующего органа (см. рис. 1.) 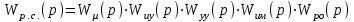 (1) (1)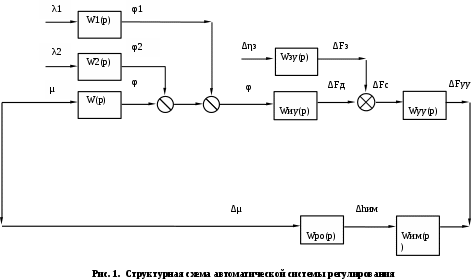 После того, как составлена передаточная функция в разомкнутом состоянии, составляется комплексная частотная функция разомкнутой системы Wр.с.(jω) и оценивается расположение годографа вектора Wр.с.(jω) относительно точки [-1,j0] при изменении ω от 0 до +∞. Критерий устойчивости Найквиста-Михайлова формулируется следующим образом: если линейная автоматическая система регулирования в разомкнутом состоянии устойчива и ее частотная характеристика Wр.с.(jω) при изменении частоты ω от 0 до +∞ не охватывает точку на комплексной плоскости с координатами [-1,j0], то после замыкания этой системы она также будет устойчивой. Если в передаточной функции Wр.с.(р) системы регулирования в разомкнутом состоянии передаточные функции составляющих систему звеньев записаны в виде 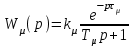 , Wи.у.(p) = kи.у., Wу.у.(p) = kу.у., Wи.м.(p) = kи.м., Wр.о.(p) = kр.о., тогда передаточная функция системы регулирования в разомкнутом состоянии , Wи.у.(p) = kи.у., Wу.у.(p) = kу.у., Wи.м.(p) = kи.м., Wр.о.(p) = kр.о., тогда передаточная функция системы регулирования в разомкнутом состоянии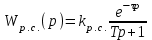 , (2) , (2)где kр.с. = kμ·kи.у.·kу.у.·kи.м.·kр.о. Запишем комплексную частотную функцию разомкнутой системы 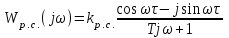 (3) (3)Умножим числитель и знаменатель в выражении комплексной частотной функции на сопряженный знаменателю множитель (Тjω–1), проведем несложные преобразования, разделим мнимую и действительную части  Выражения для действительной и мнимой частей комплексной частотной функции запишутся в виде 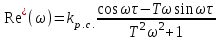 (4) (4)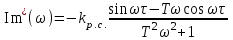 (5) (5)Амплитуда (или модуль) рассчитывается по формуле А(jω) = kр.с. 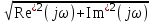 (6) (6)Фазу можно рассчитать, пользуясь выражением ψ(jω) = - arctg 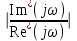 - ωτ (7) - ωτ (7)Величину ωτ необходимо при этом перевести из радиан в градусы. Расположение амплитудно-фазо-частотных характеристик разомкнутой автоматической системы регулирования на комплексной плоскости показано на рис. 2. Здесь kр.с.1 <kр.с.2 <kр.с.3. 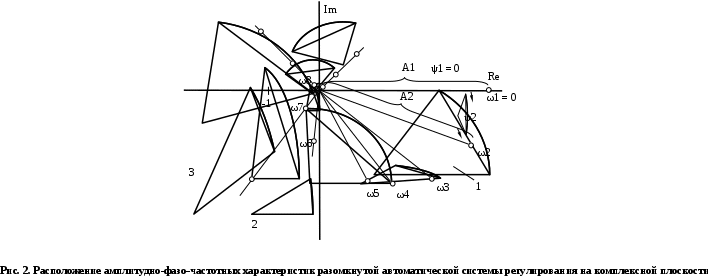 Последовательность выполнения работы Последовательность выполнения работы1. Подставляя в выражения (4) и (5) значения τ и Т, вычислить значения Re* и Im* для различных ωи kр.с.= 1. Результаты расчетов действительной и мнимой частей амплитудно-фазовых характеристик свеcти в табл. 1. 2. Пользуясь формулами (6) и (7), рассчитать значения амплитуды и фазы амплитудно-фазовых характеристик, результаты свести в табл. 2. 3. По данным табл. 2 построить расчетные амплитудно-фазовые характеристики разомкнутой автоматической системы регулирования температуры при различных значениях коэффициента передачи системы регулирования kр.с., учитывая, что kр.с. = kμ·kр, где kр - коэффициент передачи регулятора. Сделать выводы об устойчивости системы. Используя программный модуль расчета амплитудно-фазо-частотных характеристик разомкнутой автоматической системы регулирования в MathCad, рассчитать характеристики и приложить распечатки. Таблица 1 Результаты расчета действительной и мнимой частей комплексной частотной функции автоматической системы регулирования температуры диодов тяговой выпрямительной установки в разомкнутом состоянии при τ = 42 с и Т = 492 с
Таблица 2 Результаты расчета модуля и фазы комплексной частотной функции автоматической системы регулирования температуры диодов тяговой выпрямительной установки в разомкнутом состоянии при при τ = 42 с и Т = 492 с
Рекомендуемая литература Луков Н.М., Космодамианский А.С. Автоматические системы управления локомотивов: Учебник для вузов ж.-д. транспорта. – М.: ГОУ «Учебно-методический центр по образования на железнодорожном транспорте», 2007. - 427 с. Космодамианский А.С., Воробьев В.И., Пугачев А.А., Хохлов А.Д., Попов Ю.В., Стрекалов Н.Н. Автоматика и автоматические системы локомотивов. Учебное пособие. – РГОТУПС, 2008. – 97 с. Бабков Ю.В., Базилевский Ф.Ю., Грищенко А.В. Автоматизация локомотивов: Учебное пособие для вузов ж.-д. транспорта. – М.: ГОУ «Учебно-методический центр по образования на железнодорожном транспорте», 2007 – 323 с. Электрические передачи локомотивов и тяговые статические преобразователи: /Космодамианский А.С., Луков Н.М., Ромашкова О.Н, Воробьёв В.И. и др.: Уч. пос. – М.: МИИТ, 2009. – 138 с. Докт. техн. наук, проф. А.С.Космодамианский Канд. техн. наук, ст. преп. Ю.В.Попов Ст. преп. Н.Н.Стрекалов АВТОМАТИКА И МИКРОПРОЦЕССОРНАЯ ТЕХНИКА ЛОКОМОТИВОВ Руководство к выполнению лабораторных работ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

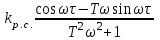
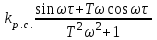
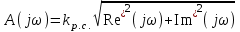
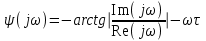 , град
, град