Карманный справочник
Русаков В.И.
Эконометрика
(Сборник определений, формул, графиков, таблиц)
Москва
НИУ «МЭИ»
2022
УДК
ББК
Р88
Русаков В. И. Эконометрика (Сборник определений, формул, графиков, таблиц). – М. : НИУ «МЭИ», 2022. – 41 с. – (Серия «Карманный справочник»).
Справочник содержит определения, формулы, графики и таблицы эконометрики и адресован студентам и преподавателям вуза.
Содержание
Введение в эконометрику 6
1. Понятие, цели и задачи эконометрики 6
2. Типы данных 7
3. Эконометрические модели 7
4. Типы зависимостей 8
5. Этапы эконометрического моделирования 9
Т.1 Элементы математической статистики 10
1.1 Операция суммирования 10
1.2 Случайные величины. Числовые характеристики 12
1.3 Статистические оценки и их свойства 15
1.4 Ковариация и корреляция 16
1.5 Проверка статистических гипотез 19
Т.2 Модель парной регрессии 20
2.1 Модель парной линейной регрессии 20
2.2 Метод наименьших квадратов (МНК) 22
2.3 Анализ вариации зависимой переменной. Коэффициент детерминации 23
2.4 Предпосылки регрессивного анализа (условия Гаусса-Маркова) 25
2.5 Нелинейные регрессии 28
Т.3 Модель множественной регрессии 30
3.1 Модель множественной линейной регрессии 30
3.3 Мультиколлинеарность. Частная корреляция 34
3.4 Спецификация переменных в уравнениях регрессии 35
3.5 Производственная функция Кобба-Дугласа 37
Т.4 Временные ряды 39
4.1 Элементы временного ряда 39
4.2 Модели временных рядов 40
Т.5 Системы одновременных уравнений 40
5.1 Структурная форма модели 40
5.2 Приведенная форма модели 41
5.3 Идентификация 42
Обозначения
= равно
≠ не равно
≈ приближённо равно
> больше
< меньше
≥ больше или равно
≤ меньше или равно
подобно
∞ бесконечность
Введение в эконометрику 1. Понятие, цели и задачи эконометрики
Эконометрика – это наука, изучающая количественные закономерности и связи в экономике методами математической статистики.
Цель эконометрики – эмпирический вывод экономических закономерностей.
Задачи эконометрики – построить модели, выражающие экономические закономерности, оценить их параметры, проверить гипотезы о закономерностях изменения и связях экономических показателей.
2. Типы данных
Данные
Пространственные данные
Временные ряды
Пространственные данные – этоданные о каком-либо экономическом показателе от разных однотипных объектов, относящиеся к одному и тому же моменту времени.
Временные ряды – это данные о каких-либо показателях, характеризующих одни и те же объекты в различные моменты времени.
3. Эконометрические модели
Три класса экономических моделей:
1) регрессионные модели с одним уравнением;
2) системы одновременных уравнений;
3) модели временных рядов.
Регрессионная модель – это уравнение, в котором объясняемая переменная представляется в виде функции от объясняющих переменных.
Системы одновременных уравнений – этосистемы уравнений, состоящие из регрессионных уравнений и тождеств, в каждом из которых помимо объясняющих-независимых переменных содержатся объясняемые переменные из других уравнений системы.
Модели временных рядов – это модели, в которых результативная переменная зависит от переменной времени.
4. Типы зависимостей
Зависимость
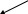 
Функциональная
Статистическая
Функциональная зависимость – это связь в виде точной формулы, в которой каждому значению одной переменной соответствует строго определенное значение другой переменной и воздействием случайных факторов при этом пренебрегают.
Статистическая зависимость – это связь переменных, на которую накладывается воздействие случайных факторов, при этом изменение одной переменной приводит к изменению математического ожидания другой переменной.
5. Этапы эконометрического моделирования
Семь этапов:
1) постановочный этап;
2) априорный этап;
3) этап параметризации;
4) информационный этап;
5) этап идентификации модели;
6) этап оценки качества модели;
7) этап интерпретации результатов моделирования.
Т.1 Элементы математической статистики 1.1 Операция суммирования
Сумма чисел:
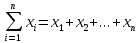
или
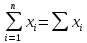
Сумма квадратов:
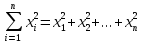
Средние значения:
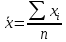
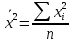
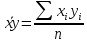
Неравенство:
Н
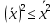
еравенство
П
равила:
1
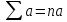
1.
(a, b - константы)
.
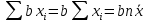
2.
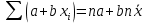
3.
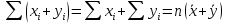
4.
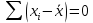
5.
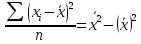
6.
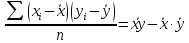
7.
1.2 Случайные величины. Числовые характеристики
Случайная величина – величина, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из множества чисел.
Случайная величина
Дискретная
Непрерывная
Дискретная случайная величина – случайнаявеличина, которая принимает отдельные, изолированные друг от друга значения.
Непрерывная случайная величина – случайная величина, множество значений которой непрерывно заполняет некоторый числовой промежуток.
Генеральная совокупность – это множество всех значений случайной величины, которые она может принять в процессе наблюдения.
Выборочная совокупность – это множество наблюдений, составляющих лишь часть генеральной совокупности.
Числовые характеристики генеральной совокупности.
Генеральная средняя 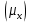 – это математическое ожидание случайной величины Х: – это математическое ожидание случайной величины Х:
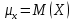
Генеральная дисперсия 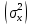 – это математическое ожидание квадрата отклонения случайной величины Х относительно ее средней: – это математическое ожидание квадрата отклонения случайной величины Х относительно ее средней:
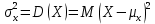
Стандартное отклонение 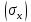 – это квадратный корень из дисперсии случайной величины Х: – это квадратный корень из дисперсии случайной величины Х:
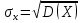
Числовые характеристики выборки.
Выборочная средняя 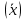 – это среднее арифметическое наблюдаемых значений случайной величины Х в выборке: – это среднее арифметическое наблюдаемых значений случайной величины Х в выборке:
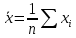
Выборочная дисперсия 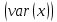 – это среднее арифметическое квадратов отклонения наблюдаемых значений случайной величины Х в выборке от их среднего значения: – это среднее арифметическое квадратов отклонения наблюдаемых значений случайной величины Х в выборке от их среднего значения:
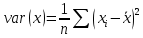
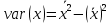
1.3 Статистические оценки и их свойства
О
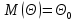
ценка Θ является несмещённой, если её математическое ожидание равно оцениваемому параметру 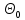 при любом объеме выборки, т.е.: при любом объеме выборки, т.е.:
Несмещённая оценка Θ называется эффективной, если она имеет минимальную дисперсию по сравнению с другими выборочными оценками, т.е.:
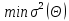
Оценка Θ называется состоятельной, если при 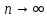 она стремится по вероятности к оцениваемому параметру она стремится по вероятности к оцениваемому параметру 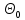 , т.е.: , т.е.:
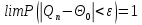
1.4 Ковариация и корреляция
Теоретическая ковариация случайной величины Х и Y – это математическое ожидание произведения отклонений этих величин от своих средних значений, т.е.:
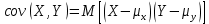
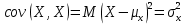
Теоретический коэффициент корреляции 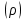 : :
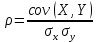
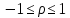
Выборочная ковариация двух переменных 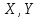 – это средняя величина произведения отклонений этих переменных от своих средних, т.е.: – это средняя величина произведения отклонений этих переменных от своих средних, т.е.:
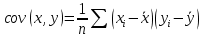
или
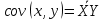 - - 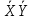
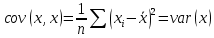
Выборочный коэффициент корреляции 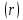 : :
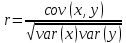

Выборочный коэффициент корреляции 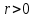 : :
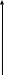
.
.
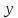

.
.
.
.
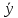
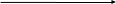
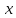
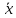
В
.
ыборочный коэффициент корреляции 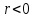 : :
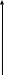 
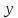
.
.
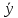
.
.
.
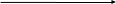
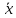
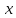
В
.
.
ыборочный коэффициент корреляции 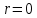 : :
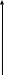
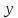
.
.
.
.
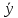
.
.
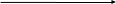
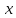
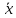
1.5 Проверка статистических гипотез
Статистическая гипотеза (Н) – это предположение относительно параметра или распределения случайной величины.
Гипотезы (Н)
 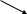
Нулевая 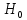
Конкурирующая 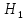
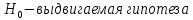

Статистический критерий – это случайная величина, которая нужна для проверки нулевой гипотезы.
Распределения
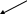 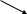
Стьюдента (t – статистика)
Фишера (F – статистика)
Уровень значимости (α) – это вероятность того, что будет отвергнута правильная нулевая гипотеза, т.е.:
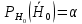
Расчётное значение критерия – это значение критерия, вычисленное по данным выборки.
Т.2 Модель парной регрессии 2.1 Модель парной линейной регрессии
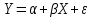
,
где X – объясняющая (независимая) переменная;
Y – объясняемая (зависимая) переменная;
α, β – параметры уравнения;
ε – случайный член (ошибка регрессии).
Выборочное уравнение регрессии:
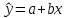
,
где 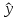 – расчетное значение переменной Y; – расчетное значение переменной Y;
a, b – оценки параметров α и β.
График уравнения регрессии
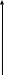
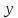
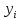
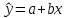

{
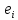
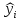
.
.
.
.
.
.
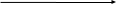
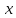
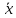
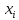
Отклонение от расчётной величины:
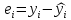
,
где 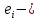 отклонение (остаток) i-ого наблюдения; отклонение (остаток) i-ого наблюдения;
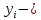 величина переменной Yвi-ом наблюдении; величина переменной Yвi-ом наблюдении;
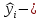 расчетная величина переменной Yвi-ом наблюдении; расчетная величина переменной Yвi-ом наблюдении;
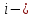 порядковый номер измерения переменных. порядковый номер измерения переменных.
2.2 Метод наименьших квадратов (МНК)
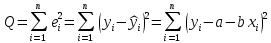
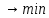
Сущность МНК: минимизация суммы квадратов остатков.
Необходимые условия минимума:
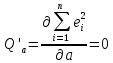
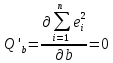
Решение системы:
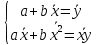
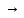
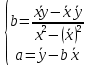
Наблюдаемые значения Y:
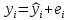
2.3 Анализ вариации зависимой переменной. Коэффициент детерминации
Выборочные дисперсии:
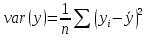
дисперсия набюдаемых значений 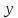
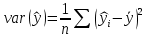
дисперсия расчетных значений 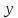
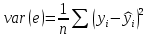
дисперсия остатков 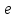
Разброс:
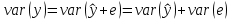
,
где 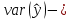 часть, объясненная регрессионным уравнением; часть, объясненная регрессионным уравнением;
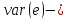 часть, не объясненная регрессионным уравнением. часть, не объясненная регрессионным уравнением.
Коэффициент детерминации (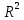 ): ):
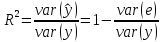
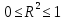

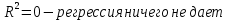
2.4 Предпосылки регрессивного анализа (условия Гаусса-Маркова)
Линейная регрессионная модель с 2-мя переменными:
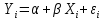
,
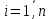
где 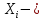 объясняющая (независимая) переменная; объясняющая (независимая) переменная;
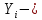 объясняемая (зависимая) переменная; объясняемая (зависимая) переменная;
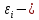 случайный членi-ого наблюдения (ошибка регрессии). случайный членi-ого наблюдения (ошибка регрессии).
Условия Гаусса-Маркова:
1. Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю, т.е.:
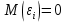
2
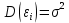
. Дисперсия случайного члена должна быть постоянна для всех наблюдений, т.е.:
3. Случайные члены должны быть независимы (некоррелированы) между собой, т.е.:
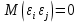
4. 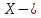 неслучайная величина. неслучайная величина.
Г
.
.
омоскедастичность:
  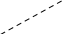
.
.

.
.
.
.
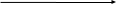
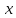
Г
.
етероскедастичность:
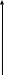 
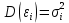
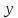
.
.
.

.
.
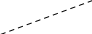
.
.
.
.
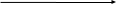
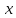
Автокорреляция – это коррелированность 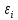 (зависимость) случайных членов для каждых двух соседних наблюдений. (зависимость) случайных членов для каждых двух соседних наблюдений.
Теорема Гаусса-Маркова:
Если предпосылки выполняются, то оценки (a, b) являются:
несмещёнными: 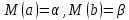 (отсутствие ошибки); (отсутствие ошибки);
эффективными: 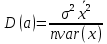 , ,  (наименьшая дисперсия); (наименьшая дисперсия);
состоятельными: 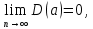 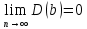 (при большом (при большом 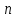 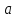 и и 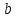 близки к близки к 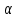 и и 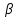 ). ).
2.5 Нелинейные регрессии
Нелинейность:
по переменным (устраняется заменой);
по параметру (устраняется логарифмированием).
Например:
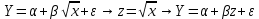
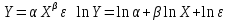
Эластичность функции 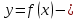 это отношение относительного изменения это отношение относительного изменения 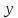 к относительному изменению к относительному изменению 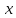 , т.е.: , т.е.:
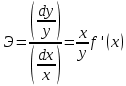
Т.3 Модель множественной регрессии
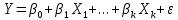
,
где 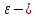 случайный член; случайный член;
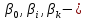 параметры модели; параметры модели;
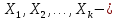 объясняющие (нез-е) переменные; объясняющие (нез-е) переменные;
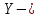 объясняемая (зависимая) переменная. объясняемая (зависимая) переменная.
Выборочное уравнение регрессии:
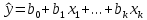
,
где 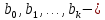 оценки параметров оценки параметров 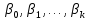 . .
Метод наименьших квадратов:
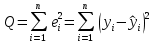
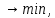
где 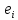 остаток в i-ом варианте; остаток в i-ом варианте;
n – число вариантов (наблюдений)
Оценки параметров модели и теоретической дисперсии в матричной форме:
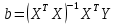
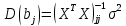
где 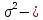 дисперсия случайного члена; дисперсия случайного члена;
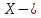 матрица значений объясняющих переменных; матрица значений объясняющих переменных;
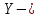 вектор значений зависимой переменной; вектор значений зависимой переменной;
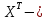 транспонированная матрица. транспонированная матрица.
Остаточная дисперсия:
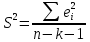
Стандартные ошибки коэффициентов 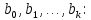
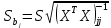
S – стандартная оценка регрессии
3.2 Анализ вариации зависимой переменной
Дисперсия зависимой переменной:
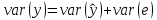
,
где 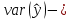 объяснённая составляющая; объяснённая составляющая;
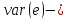 необъяснённая составляющая. необъяснённая составляющая.
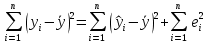
,
TSS
ESS
USS
где TSS – общий разброс зависимой переменной;
ESS – разброс, объяснённый регрессией;
USS – разброс, необъясненный регрессией.
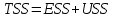
,
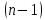
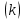
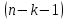
где 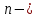 число наблюдений (вариант); число наблюдений (вариант);
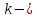 число объясняющих переменных. число объясняющих переменных.
Коэффициент детерминации 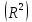 : :
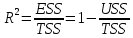
Скорректированный коэффициент детерминации 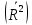 : :
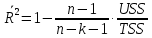
3.3 Мультиколлинеарность. Частная корреляция
Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии.
Корреляционная матрица
Коэффициент частной корреляции:
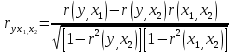
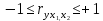
3.4 Спецификация переменных в уравнениях регрессии
Влияние отсутствия 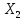 : :
Было: 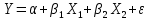
Стало: 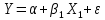
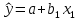
Тогда: 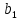 является смещённой, а является смещённой, а 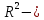 завышенной оценкой. завышенной оценкой.
Влияние включения 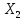 : :
Было: 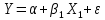
Стало: 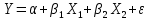
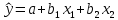
Тогда: 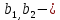 несмещённые, но не эффективные. несмещённые, но не эффективные.
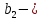 незначим и незначим и 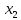 исключается. исключается.
Замещающие переменные:
Было: 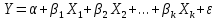
Стало: 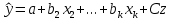
Тогда: 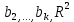 такие же, но такие же, но 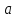 не является оценкой не является оценкой 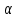 . .
Лаговые переменные:
Есть: 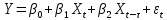
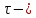 лаг-сдвиг, характеризующий запаздывание. лаг-сдвиг, характеризующий запаздывание.
Инструментальные переменные:
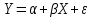
ИП – метод инструментальных переменных.
Суть ИП: замена переменной, некореллированной со случайным членом, но кореллированной с исходной переменной.
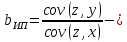 состоятельная, но смещенная и не эффективная. состоятельная, но смещенная и не эффективная.
Ф
Значения
иктивные переменные:
1
признак присутствует
|
0
признак отсуствует
|
Фиктивные переменные улучшают качество оценивания.
3.5 Производственная функция Кобба-Дугласа
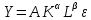

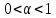
,
ПФ К-Д:
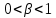
где 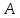 , , 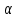 , , 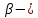 параметры модели; параметры модели; 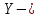 объем выпуска; объем выпуска; 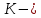 капитальные затраты; капитальные затраты; 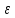 - затраты труда. - затраты труда.
Свойства произв-ной функции Кобба-Дугласа:
1. Эластичность выпуска продукции
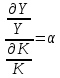
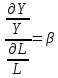
Эластичность по капиталу и труду.
2. Эффект от масштаба производства
если 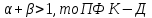 возрастает; возрастает;
если 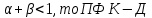 убывает; убывает;
если 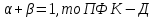 постоянна. постоянна.
3. Прогнозируемые доли производственных факторов
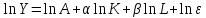
Т.4 Временные ряды 4.1 Элементы временного ряда
В
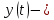 уровень временного ряда уровень временного ряда
ременной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов времени.
Факторы:
1) длительные (постоянно действующие) 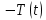 ; ;
2) кратковременные (периодические)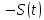 ; ;
3) случайные (случайные изменения)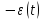 . .
4.2 Модели временных рядов
Модели:
1
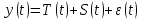
. Аддитивная:
2
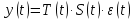
. Мультипликативная:
Т.5 Системы одновременных уравнений 5.1 Структурная форма модели
Структурная форма модели – это система уравнений, в каждом из которых аргументы помимо объясняющих переменных могут включать в себя также объясняемые переменные из других уравнений системы.
Например, простейшая структурная форма модели:
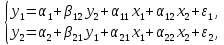
где 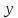 и и 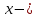 значения зависимой и независимой переменной; значения зависимой и независимой переменной;
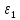 и и 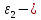 случайные члены; случайные члены;
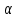 и и 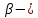 параметры модели (структурные коэффициенты). параметры модели (структурные коэффициенты).
Эндогенные переменные («эндо» - внутреннее) – это переменные, значения которых определяются внутри модели и являются зависимыми переменными.
Экзогенные переменные («экзо» - внешнее) – это переменные, значения которых определяются вне модели и являются независимыми переменными.
5.2 Приведенная форма модели
Приведённая форма модели – это система уравнений, в каждом из которых эндогенные переменные выражены только через экзогенные переменные и случайные составляющие.
Например:
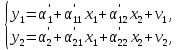
где 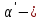 параметры приведенной формы; параметры приведенной формы;
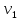 и и 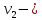 случайные члены. случайные члены.
5.3 Идентификация
Идентификация – этоединственность соответствия между приведённой и структурной формами модели.
Структурные коэффициенты:
а) идентифицируемые;
б) сверхидентифицируемые;
в) неидентифицируемые.
Структурное уравнение называется идентифицируемым, если идентифицируемы все его коэффициенты.
Модель считается идентифицируемой, если каждое её уравнение идентифицируемо.
|
 Скачать 107.8 Kb.
Скачать 107.8 Kb.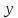
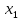
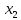
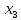
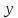
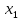
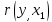
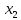
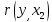
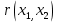
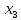
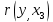
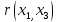
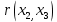
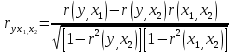
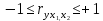
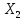 :
: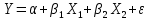
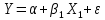
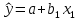
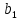 является смещённой, а
является смещённой, а 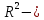 завышенной оценкой.
завышенной оценкой.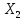 :
: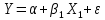
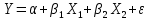
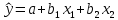
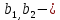 несмещённые, но не эффективные.
несмещённые, но не эффективные.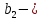 незначим и
незначим и 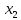 исключается.
исключается.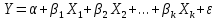
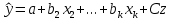
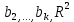 такие же, но
такие же, но 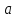 не является оценкой
не является оценкой 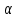 .
.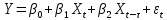
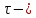 лаг-сдвиг, характеризующий запаздывание.
лаг-сдвиг, характеризующий запаздывание.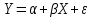
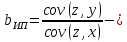 состоятельная, но смещенная и не эффективная.
состоятельная, но смещенная и не эффективная.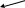
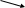
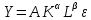

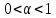
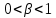
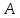 ,
, 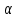 ,
, 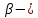 параметры модели;
параметры модели; 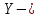 объем выпуска;
объем выпуска; 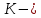 капитальные затраты;
капитальные затраты; 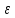 - затраты труда.
- затраты труда. 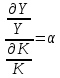
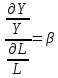
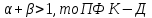 возрастает;
возрастает;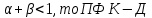 убывает;
убывает;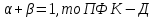 постоянна.
постоянна.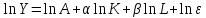
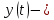 уровень временного ряда
уровень временного ряда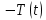 ;
;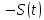 ;
;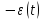 .
.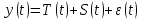

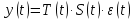
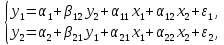
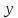 и
и 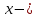 значения зависимой и независимой переменной;
значения зависимой и независимой переменной;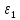 и
и 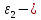 случайные члены;
случайные члены;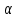 и
и 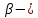 параметры модели (структурные коэффициенты).
параметры модели (структурные коэффициенты).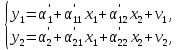
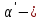 параметры приведенной формы;
параметры приведенной формы;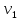 и
и 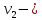 случайные члены.
случайные члены.
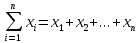
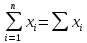
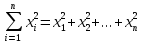
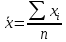
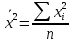
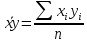
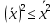
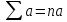
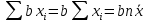
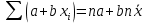
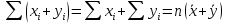
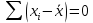
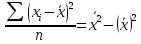
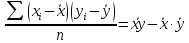
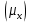 – это математическое ожидание случайной величины Х:
– это математическое ожидание случайной величины Х: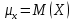
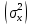 – это математическое ожидание квадрата отклонения случайной величины Х относительно ее средней:
– это математическое ожидание квадрата отклонения случайной величины Х относительно ее средней: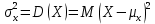
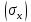 – это квадратный корень из дисперсии случайной величины Х:
– это квадратный корень из дисперсии случайной величины Х: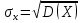
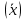 – это среднее арифметическое наблюдаемых значений случайной величины Х в выборке:
– это среднее арифметическое наблюдаемых значений случайной величины Х в выборке: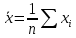
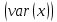 – это среднее арифметическое квадратов отклонения наблюдаемых значений случайной величины Х в выборке от их среднего значения:
– это среднее арифметическое квадратов отклонения наблюдаемых значений случайной величины Х в выборке от их среднего значения: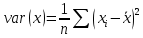
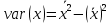
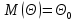
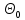 при любом объеме выборки, т.е.:
при любом объеме выборки, т.е.: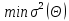
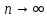 она стремится по вероятности к оцениваемому параметру
она стремится по вероятности к оцениваемому параметру 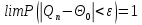
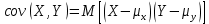
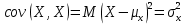
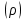 :
: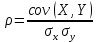
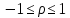
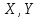 – это средняя величина произведения отклонений этих переменных от своих средних, т.е.:
– это средняя величина произведения отклонений этих переменных от своих средних, т.е.: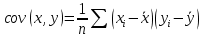
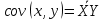 -
- 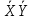
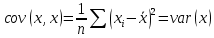
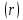 :
: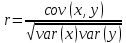

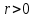 :
: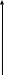

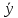
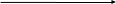
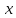
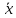
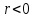 :
:
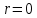 :
: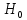
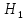
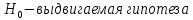

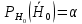
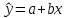
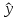 – расчетное значение переменной Y;
– расчетное значение переменной Y;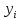

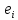
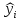
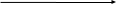
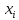
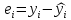
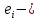 отклонение (остаток) i-ого наблюдения;
отклонение (остаток) i-ого наблюдения;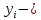 величина переменной Yвi-ом наблюдении;
величина переменной Yвi-ом наблюдении;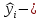 расчетная величина переменной Yвi-ом наблюдении;
расчетная величина переменной Yвi-ом наблюдении;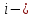 порядковый номер измерения переменных.
порядковый номер измерения переменных.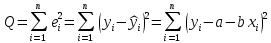
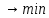
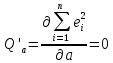
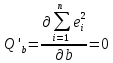
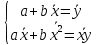
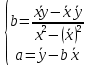
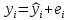
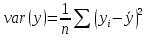
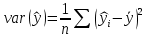
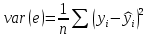
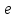
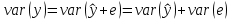
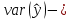 часть, объясненная регрессионным уравнением;
часть, объясненная регрессионным уравнением;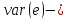 часть, не объясненная регрессионным уравнением.
часть, не объясненная регрессионным уравнением.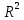 ):
):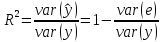
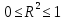

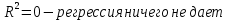
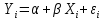
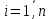
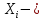 объясняющая (независимая) переменная;
объясняющая (независимая) переменная;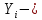 объясняемая (зависимая) переменная;
объясняемая (зависимая) переменная;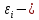 случайный членi-ого наблюдения (ошибка регрессии).
случайный членi-ого наблюдения (ошибка регрессии).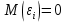
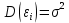
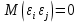
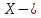 неслучайная величина.
неслучайная величина.
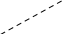


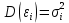
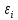 (зависимость) случайных членов для каждых двух соседних наблюдений.
(зависимость) случайных членов для каждых двух соседних наблюдений.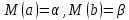 (отсутствие ошибки);
(отсутствие ошибки);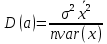 ,
,  (наименьшая дисперсия);
(наименьшая дисперсия);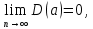
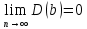 (при большом
(при большом 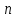
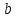 близки к
близки к 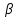 ).
).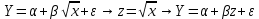
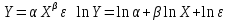
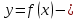 это отношение относительного изменения
это отношение относительного изменения 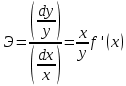
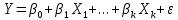
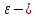 случайный член;
случайный член;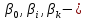 параметры модели;
параметры модели;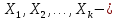 объясняющие (нез-е) переменные;
объясняющие (нез-е) переменные;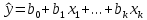
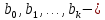 оценки параметров
оценки параметров 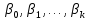 .
.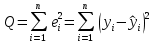
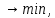
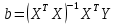
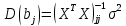
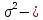 дисперсия случайного члена;
дисперсия случайного члена;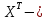 транспонированная матрица.
транспонированная матрица.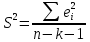
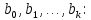
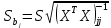
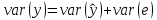
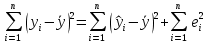
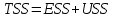
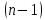
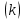
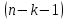
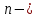 число наблюдений (вариант);
число наблюдений (вариант);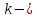 число объясняющих переменных.
число объясняющих переменных.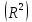 :
: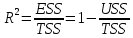
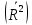 :
: