С целью проведения дисперсионного анализа
 Скачать 226.5 Kb.
|
|
7.4. Планирование однофакторного эксперимента В классической теории эксперимента рассматриваются планы, составленные с целью проведения дисперсионного анализа определенного вида. Поэтому естественно, что исходной посылкой служит цель исследования. Исходя из нее, формируется представление о виде предполагаемой математической модели явления, числе исследуемых факторов и их уровнях (см. § 6.1). Простейшим в этом контексте следует считать однофакторный эксперимент, который призван установить факт зависимости результата эксперимента от значения исследуемого единственного фактора, т.е. влияние других факторов предполагается несущественным. Рассмотрим подробно последовательность действий для построения плана такого эксперимента на конкретном примере. ПРИМЕР. Исследование влияния срока хранения на качество ГСМ. Подразумевается существование такого единственного измеримого параметра y, который характеризует качество ГСМ и который может зависеть от некоторых входных факторов X. Так как измерительная аппаратура имеет погрешность, то для исследования влияния срока хранения на параметр y необходимо производить многократные рандомизированные его замеры при различных сроках хранения, например, по n замеров в течение нескольких (m) месяцев. (Задавшись определенными требованиями к достоверности выводов, с помощью методик, рассмотренных в § 7.3, можно определить необходимый объем эксперимента, т.е. значения n и m.) Весь массив данных в таком случае удобно сформировать в виде (табл. 18) матрицы результатов эксперимента  где j = 1, 2,..., m – номер значения (уровня) исследуемого фактора (срока хранения – месяца), а i = 1, 2,..., n – порядковый номер замера качества y (в течение каждого месяца). Таким образом, планируемый эксперимент оказывается многоуровневым – m-уровневым.Таблица 18.
Для последующего дисперсионного анализа необходимо задать вид математической модели. Он определяется исследуемым явлением и той гипотезой, которая проверяется. Выдвинем гипотезу о том, что срок хранения T влияет на характеристику качества ГСМ y. Тогда естественно представить себе математическую модель для дисперсионного анализа (дисперсионную модель) исследуемого влияния в виде:  где – математическое ожидание генерального значения параметра y за весь исследуемый срок,  – добавок к от влияния исследуемого фактора (срока хранения в течении j месяцев),  – нормально распределенная погрешность в каждом единичном опыте (i-ом замере в j-ом месяце).В унифицированном виде, принятом в планировании эксперимента, матрица такого плана (табл. 19) содержит n m строк, соответствующих единичным опытам. Таблица 19.
Этот план полностью рандомизированного однофакторного многоуровневого эксперимента позволяет произвести дисперсионный анализ (§ 6.3) и выявить влияние исследуемого единственного фактора. Для этого, как это принято в дисперсионном анализе, разбивают статистическую оценку общей дисперсии:  где  на две части: остаточную – внутреннюю, отражающую разброс результатов единичных опытов вокруг средних по группам экспериментальных данных каждого месяца, обусловленную неконтролируемой погрешностью эксперимента: 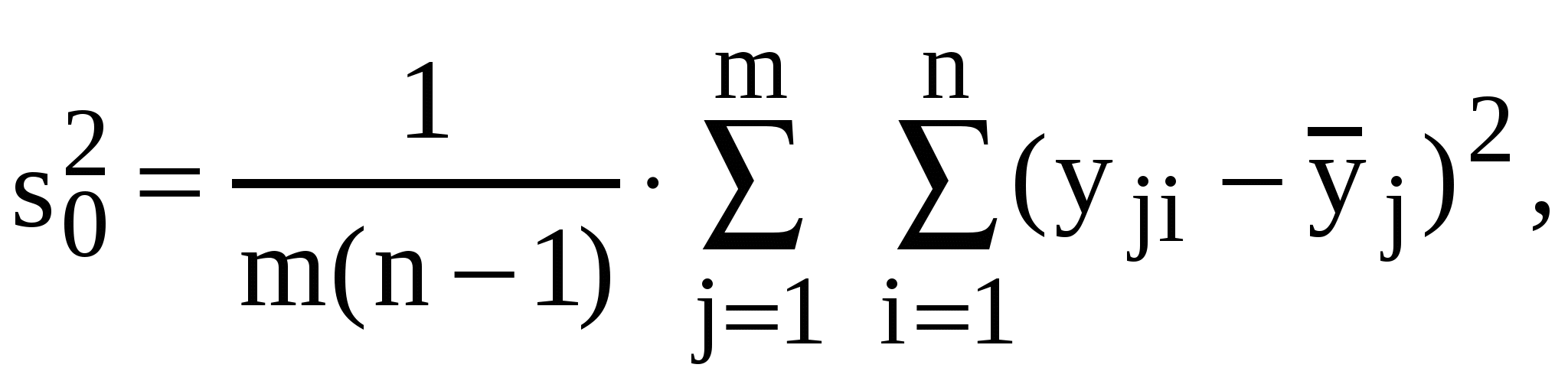 и межгрупповую, отражающую разброс средних (месячных) экспериментальных данных между собой из-за влияния исследуемого фактора:  .Далее оценку значимости фактора T (зависимости качества ГСМ от срока хранения) получают с помощью критерия Фишера для сравнения двух дисперсий при уровне значимости (строка 13 табл. 10). Если 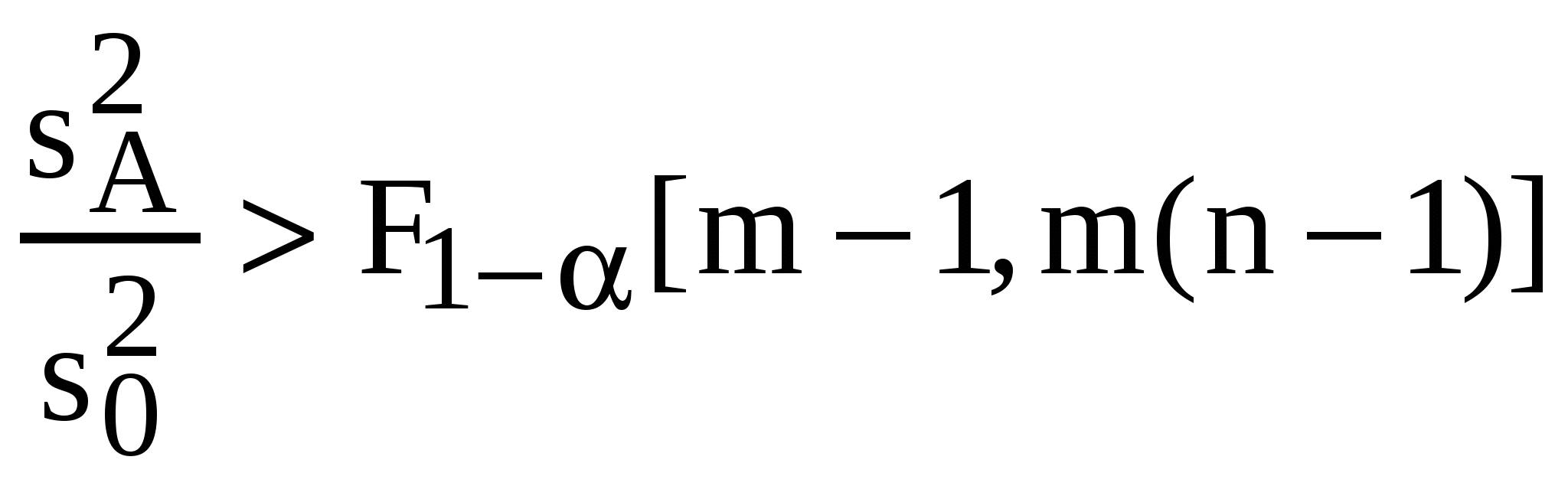 ,то значимое превышение  над  свидетельствует о значимости фактора T, т.е. о существовании выраженной зависимости y от T (качества ГСМ от срока хранения). В этом случае можно оценить дисперсию влияния исследуемого фактора величиной:  Если наоборот: 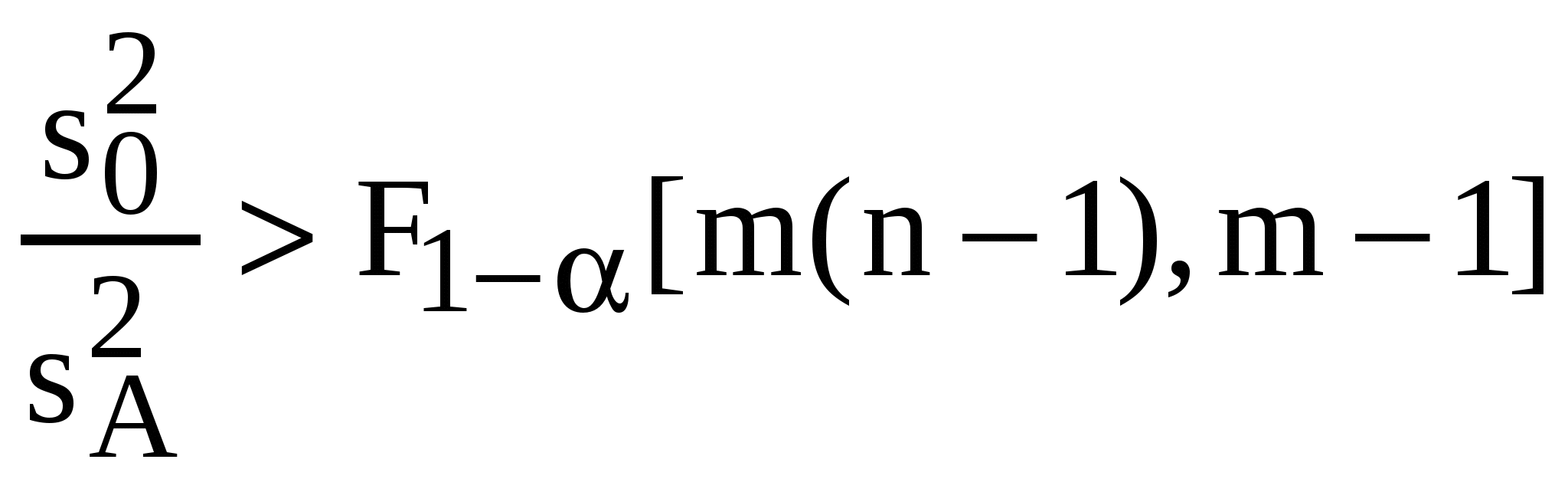 ,то  значимо меньше  , т.е. случайной погрешности эксперимента, поэтому влияние фактора T на y несущественно и им можно пренебречь. В этом случае в качестве оценки погрешности (дисперсии) следует использовать выражение общей дисперсии  , имеющей число степеней свободы большее, чем и . В случае, когда нельзя говорить о значимом превосходстве одной из дисперсий над другой, влияние исследуемого входного фактора сравнимо с погрешностью эксперимента или влиянием неучтенных факторов, поэтому конкретный вывод невозможен.7.5. Планирование двухфакторного эксперимента План двухфакторного эксперимента рассмотрим на примере задачи об испытаниях шин. ПРИМЕР. Пусть для испытания выделено 12 шин новой марки и 4 типа автомобиля: I, II, III, IV; а технические условия таковы, что перестановка колес во время испытания исключается. В этом эксперименте предполагается наличие двух существенных факторов: T – автомобиль и S – место установки шины на автомобиле, распознаваемое по условным номерам: 1, 2, 3, 4. Таким образом, количество уровней каждого фактора оказывается равным 4. Легко видеть, что рассматриваемые факторы независимы, поэтому можно не исследовать третий фактор их совместного влияния. Математическая дисперсионная модель такого эксперимента может быть записана в виде:  где  – результат испытания шины на i-м месте j-го автомобиля; – средний ожидаемый результат (математическое ожидание);  – отклонение от , обусловленное влиянием типа автомобиля;  – отклонение от  , обусловленное влиянием места установки шины на автомобиле;  – нормально распределенная погрешность оценки результата эксперимента, обусловленная влиянием неучтенных факторов.Естественное стремление поставить эксперимент наиболее полным образом для данного примера означает, что надо было бы испытать шины на каждом месте всех автомобилей. Т.е. провести полный факторный эксперимент, обеспечивающий всевозможные сочетания всех уровней и всех факторов, объемом  опытов, где k = 2 – число факторов, а  = 4 – число уровней каждого фактора. Наличие только 12 шин не позволяет построить полный план такого эксперимента. Как же следует разместить шины с наибольшей выгодой для наибольшей представительности результатов? Если попытаться разместить шины, полностью укомплектовав первые 3 типа автомобилей, то последний окажется не у дел. В целях экономии средств это может быть и выгодно, но не позволит получить информацию об эксплуатационных свойствах шин на четвертом типе автомобиля. Однако с формальной точки зрения такой способ обладает существенным преимуществом перед другими – полнотой. Мы получаем полный план двухфакторного эксперимента для 3 уровней фактора типа автомобиля и 4 уровней фактора места расположения шин. В этом примере очевидно, что полнота плана без дополнительных усилий влечет за собой его сбалансированность – симметричность распределения отдельных опытов в эксперименте, т.е. в нашем примере расположение шин на каждом из трех автомобилей симметрично. Кроме того, нет нужды заботиться о рандомизации – в рамках рассматриваемой задачи различие между шинами не исследуется, а сбалансированность полного плана ставит исследуемые факторы в равные условия. Аналогичные рассуждения можно провести для размещения шин на трех определенных местах (например, за исключением 4-го) всех 4 автомобилей. Эти неудачные попытки наводят на мысль о неизбежности построения неполного плана. Размещение 12 шин на 4 местах 4 автомобилей возможно только группами – блоками (сериями). Блоки можно рассматривать как по автомобилям, так и по местам расположения. В нашем примере блоки не могут быть полными – шины будут испытываться не на каждом месте каждого автомобиля: план эксперимента оказывается неполноблочным. Таблица 20.
Стремление получить как можно более полную информацию подталкивает к построению сбалансированных блоков: на каждом автомобиле разместить по 3 шины так, чтобы любые два места расположения встречались одинаковое число раз. А рандомизацию исследуемых факторов можно обеспечить случайным распределением незанятых номеров мест между автомобилями или полным перебором таковых. Таблица 21.
Таким образом, мы приходим к неполноблочному сбалансированному плану двухфакторного четырехуровневого рандомизированного эксперимента, изображенному в табл. 20. В ней номер строки (места) можно интерпретировать, как номер отдельного опыта для определения результата испытаний шин на данном месте установки. Аналогичные рассуждения допустимы и относительно номера столбца (автомобиля). Т.е. возникает множество возможностей изображать один и тот же план одного и того же эксперимента. Исходным в нашем примере является представление об опыте, связанном с испытанием одной шины. Поэтому более естественным представляется изображение плана эксперимента в унифицированной форме, показанной в табл. 21. Матрица этого плана выглядит несколько непривычно для своего "названия", однако, она дает четкое изображение уровней всех исследуемых факторов для каждого опыта (т.е. где устанавливается каждая шина). 7.6. Планирование многофакторного эксперимента Рассмотрим расширение примера предыдущего параграфа на случай трех факторов. ПРИМЕР. Для испытаний выделено по 4 шины 4 марок A, B, C, D и 4 типа автомобиля: I, II, III, IV. Перестановка колес во время испытаний исключается. В этом эксперименте присутствуют 3 существенных фактора: T – тип автомобиля, S – место установки шины на автомобиле, распознаваемое по условным номерам: 1, 2, 3, 4, и Q – тип шины. Как и в предыдущем параграфе, количество уровней каждого фактора равно 4 и факторы независимы. Математическая дисперсионная модель такого эксперимента, не исследующего совместное влияние факторов, может быть записана в виде:  где  – результат испытания шины m-ой марки на i-м месте j-го автомобиля;  – отклонение от  (см. § 7.5), обусловленное влиянием m-й марки шины;  – погрешность эксперимента, обусловленная влиянием неучтенных факторов.Таблица 22.
Полный факторный эксперимент в этом случае требует 4 4 4 = 64 опыта, т.е. 64 шины. В нашем распоряжении их только 16, что позволяет полностью обеспечить ими все автомобили. Поэтому, несмотря на то, что весь план неполный, блоки в нем можно сделать полными и рандомизированными, т.е. установить на каждый автомобиль в случайном порядке все четыре типа шин. В таком случае составить сбалансированный рандомизированный план помогают латинские квадраты (см. § 7.2). Такой план в двух разных видах представлен в табл. 22 и 23. Таблица 23.
Как видно из рассмотренных примеров, образное представление многофакторных планов с числом уровней больше 2, весьма затруднено. Поэтому для изучения особенностей таких планов будем в дальнейшем рассматривать только двухуровневые факторы. Таблица 25.
Не случайно план табл. 25 совпадает с планом табл. 15 § 7.2 в задаче о взвешивании. И тот и другой являются сбалансированным полноблочным планом трехфакторного двухуровневого, полностью рандомизированного эксперимента для дисперсионного анализа. Нетрудно видеть, что план эксперимента табл. 25, обеспечивающий получение результатов y1, y2, y3 и y4, предоставляет принципиальную возможность провести и другие виды статистического анализа: регрессионный и корреляционный. Прежде, чем перейти к обсуждению этой возможности, введем некоторые определения, характеризующие свойства плана. Обозначим элементы матрицы плана через  . Тогда для столбцов j = 1, 2, 3 легко убедиться в следующем:1) сумма элементов любого столбца равна нулю:  ,где N – число опытов; это свойство говорит о том, что план симметричный; 2) сумма квадратов элементов столбца (длина столбца) на единицу больше числа k факторов:  ,– это условие нормировки, а k + 1 называется числом степеней свободы плана; 3) скалярное произведение любых двух различных столбцов плана равно нулю: 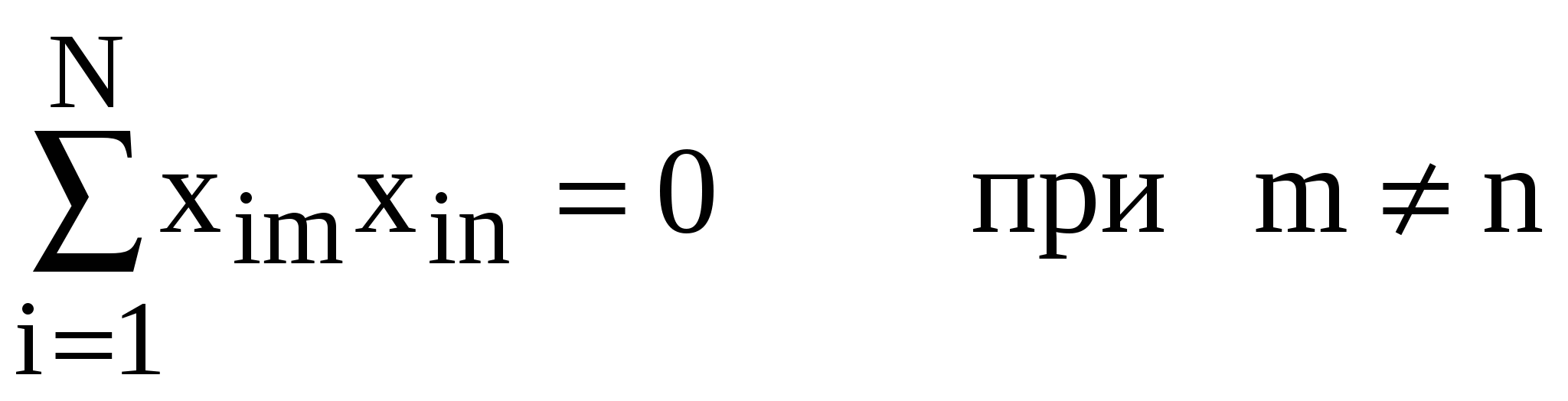 ,это свойство носит название ортогональности (оно приводит к независимости определения всех коэффициентов линейной регрессионной модели); 4) число опытов N совпадает с числом коэффициентов уравнения линейной регрессии k + 1 – в этом случае план называется насыщенным для выбранной линейной регрессионной модели. Действительно: по 4 результатам эксперимента можно определить все 4 коэффициента линейной по трем факторам регрессии исследуемого параметра y: y = 0 + 1x1 + 2x2 + 3x3. Следует обратить внимание на то, что понятие насыщенности связано именно с линейной регрессионной математической моделью исследуемого явления. В случае N > k + 1 план ненасыщенный – определение всех коэффициентов линейной регрессионной модели не исчерпывает собранную информацию, не использует все степени свободы плана. В этом случае кроме коэффициентов регрессии можно получить дополнительные статистические оценки, например, проверить гипотезу о равенстве нулю коэффициента регрессии совместного влияния пары факторов, или построить доверительные интервалы для коэффициентов регрессии, или провести параллельно дисперсионный анализ. При насыщенном плане это невозможно. В случае N < k + 1 план сверхнасыщенный и позволяет получить оценки только части коэффициентов линейной регрессии. Таблица 26.
Заметим, что оценки для коэффициентов линейной регрессии  получаются с дисперсией  , в N раз меньшей, чем результат каждого опыта. Для определения  можно воспользоваться теми же соображениями, что и для других коэффициентов. Однако получающаяся формула свободного члена  нарушает единообразие. Поэтому модернизируем план за счет дополнительного фиктивного фактора x0 "прочих" влияний, которые всегда присутствуют, при всех опытах эксперимента. Новый вид плана представлен в табл. 26, где фигурной скобкой помечен собственно план. Симметричная матрица, представляющая этот план, в которой первый столбец, первая строка и главная диагональ состоят из +1, а все остальные элементы –1, называется матрицей Адамара.В заключение данного параграфа отметим, что составленный в табл. 26 сбалансированный полноблочный план трехфакторного двухуровневого, полностью рандомизированного эксперимента для дисперсионного анализа обладает свойствами симметричности, ортогональности и насыщенности для линейной регрессионной модели, для него также выполнено условие нормировки. Однако этот план не является полным, так как вместо  опытов содержит только 4. Но, несмотря на это, план позволяет провести линейный регрессионный анализ по всем трем факторам. 7.7. Неполные и неортогональные планы В конце предыдущего параграфа было отмечено, что план эксперимента по табл. 26 неполный, хотя и позволяет построить линейную регрессионную модель, являясь для нее насыщенным. Таблица 27.
Дополним его, для чего добавим всевозможные строки, в которых уровень +1 встречается дважды, и строку со всеми –1. В табл. 27 показан такой план. Вообще говоря, полный план можно составлять, руководствуясь следующим правилом, обеспечивающим полный перебор всевозможных комбинаций двух уровней основных факторов (кроме фиктивного x0). В первом столбце знаки меняют через один. Во втором знаки встречаются пáрами, т.е. чередуются через 2. В третьем – четверками, чередуясь через 4. Далее, если необходимо – через следующие степени 2. Построенный по этому правилу полный план всегда обладает свойствами симметричности и ортогональности, что можно проверить непосредственно. Нетрудно видеть, что план табл. 27 соответствует этому правилу построения, если в нем изменить порядок строк (опытов) на следующий: 1, 7, 6, 4, 5, 3, 2, 8. Новый план стал полным – его объем стал равняться 23 = 8, чего мы и добивались, но теперь нарушилось свойство насыщенности для линейной регрессии. Для нее план стал ненасыщенным. Следовательно, есть возможность расширения регрессионной модели на столько членов, на сколько объем эксперимента (число опытов) N стал больше числа степеней свободы k + 1. В нашем | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
