экономические задачи в ЕГЭ математика. Самое необходимое для решения задачи экономического содержания в егэ по математике (профильный уровень)
 Скачать 397.05 Kb. Скачать 397.05 Kb.
|
 Экзамен – это испытание не только знаний, но и хладнокровия, и способности действовать в сложной ситуации. На ЕГЭ по математике экономические задачи, пугают многих выпускников. Действительно ли настолько страшны «банковские» задачи? Выпускникам необходимо преодолеть страх, выработать уверенность, чтобы ученик мог сказать себе: «Да, задача необычная, но я знаю общий подход к решению таких задач – справлюсь и на этот раз». Самое необходимое для решения задачи экономического содержания в ЕГЭ по математике (профильный уровень) 1) 1% - это 0,01 2) Основные соотношения и выражениями, встречающиеся при решении задач на проценты: Число a составляет p% от числа в: a = 0,01bp Число а увеличили на p%: a·(1+0,01p) Число а увеличили сначала на p%, а потом еще наq%: a·(1+0,01p)·(1+0,01q) Число а уменьшили на p%: a·(1 - 0,01p) Задачи, связанные с изменением величины Пусть So – первоначальная величина, S – новая величина. Повышение на a% n раз на a% S= So ·(1+0,01a) S= So ·(1+0,01a)n Понижение на a% n раз на a% S= So·(1-0,01a) S= So·(1-0,01a)n Тематика задач экономического содержания в ЕГЭ по математике (профильный уровень) Задачи на кредиты с равными платежами Задачи на кредиты с дифференцированными платежами Задачи на вклады и инвестиции Задачи на наибольшее и наименьшее значение, решаемые при помощи производной Остановимся подробнее на первых двух типах: 1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет». К первому типу относятся также все задачи, где известны платежи (или дана закономерность именно для платежей). 2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами». Ко второму типу относятся также задачи, где известна закономерность уменьшения суммы долга. В задачах первого типа часто применяется формула суммы n членов геометрической прогрессии. В задачах второго типа – формула суммы n членов арифметической прогрессии.
Вообще к первому типу можно отнести все задачи, где одинаковы (или известны) платежи. Ко второму – задачи, где равномерно (или по известной схеме) уменьшается сумма долга. Задачи на погашение кредита равными платежами. Общая формула. 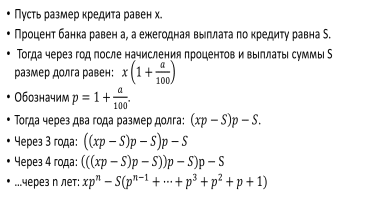 Для подсчета величины в скобках иногда применяется формула суммы n членов геометрической прогрессии. Для подсчета величины в скобках иногда применяется формула суммы n членов геометрической прогрессии.Здесь b1 =1, q = p. Напомним формулу для суммы n членов геометрической прогрессии: 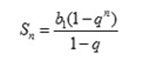 В нашем случае, размер долга через n лет 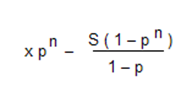 Примеры решения задач экономического содержания первого типа. Пример № 1. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить некоторую часть долга Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)? Пусть S (рублей) - нужно платить ежегодно. 1 год: В январе сумма долга составит 8052000*1,2 = 9 662 400. После 1 платежа сумма долга станет равна 9 662 400 - S. 2 год: В январе сумма долга составит (9 662 400 - S)*1,2. После 2 платежа сумма долга станет равна (9 662 400 - S)*1,2 - S. 3 год: В январе сумма долга составит ((9 662 400 - S)*1,2 - S)*1,2. После выплаты сумма долга станет равна ((9 662 400 - S)*1,2 - S)*1,2 - S. 4 год: В январе сумма долга составит (((9 662 400 - S)*1,2 - S)*1,2 - S)*1,2. После 4 платежа сумма долга станет равна (((9662400 - S)*1,2 - S)*1,2 - S)*1,2 - S. Так как кредит был погашен 4 равными платежами, то после 4 платежа долга не осталось, т.е. (((9 662 400 - S)*1,2 - S)*1,2 - S)*1,2 - S = 0. Решим это уравнение и найдем S. ((9 662 400*1,2-1,2 S - S)*1,2 - S)*1,2 - S = 0, (9 662 400*1,22 - 2,64 S-S)*1,2 - S = 0, 9 662 400*1,23 - 4,368 S - S = 0, 5,368 S = 9662400*1,23, S = 3 110 400 Ответ: 3 110 400 Пример №2 В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,16 млн. рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за 3 года)? Пусть в банке было взято X млн. руб. 1 год: В январе сумма долга будет составлять 1,2 X. После 1 платежа сумма долга составит: 1,2 X - 2,16. 2 год: В январе сумма долга будет составлять 1,2⋅(1,2X−2,16)=1,44⋅X−2,592. После 2 платежа сумма долга составит: 1,44⋅X−1,2⋅2,16−2,16=1,44⋅X−4,752. 3 год: В январе сумма долга будет составлять 1,2⋅(1,44⋅X−4,752)=1,728⋅X−5,7024. После 3 платежа сумма долга составит: 1,728⋅X−5,7024−2,16=1,728⋅X−7,8624. Так как кредит был погашен 3 равными платежами, то после 3 платежа долга не останется, т.е. станет равным 0. 1,728⋅X−7,8624=0 1,728⋅X=7,8624 X=4,55 То есть в банке было взято 4,55 млн. руб. Ответ: 4,55 Пример №3   Примеры решения задач экономического содержания второго типа. Пример № 1. 15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы: — 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца; — к 15-му числу 21-го месяца кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей? Прежде всего, введем переменные. Расчеты будем вести в тысячах рублей. Пусть S – сумма, которую планируется взять в кредит, Z – общая сумма выплат, Z = 1604 (тыс. рублей). Х - ежемесячная выплата, Х = 30 (тысяч рублей), p=3% - процент, начисляемый банком ежемесячно. После первого начисления процентов сумма долга равна Определим, к какому типу относится задача. Долг уменьшается равномерно (по условию, 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца). Значит, это задача второго типа. А в задачах второго типа мы рисуем следующую схему:  После первого начисления процентов сумма долга равна kS. Затем, после первой выплаты, сумма долга равна S – X, где Х = 30 (тысяч рублей). Значит, первая выплата равна kS – (S – X) (смотри схему). Вторая выплата: k (S – X ) – ( S – 2X). … Последняя выплата: k ( S – 20 X). Найдем общую сумму выплат Z. Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – 20X) = = k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X). Мы сгруппировали слагаемые, содержащие множитель k, и те, в которых нет k. Упростим выражения в скобках: k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) = Z. В задачах этого типа (когда сумма долга уменьшается равномерно) применяется формула для суммы арифметической прогрессии: В этой задаче мы тоже ее используем. Получим: k (21 S – 210X ) – 20 S + 210 Х= S (21k – 20) – 210 X (k-1) = Z. Осталось подставить числовые значения. S ( 21⋅ 1,03 – 20) – 210 ⋅ 30 ⋅ 0,03 = 1604. Отсюда S = 1100 тысяч рублей = 1 100 000 рублей. Следующая задача относится к тому же типу. Математическая модель та же самая. Только найти нужно другую величину – процент, начисляемый банком. К тому же количество месяцев, на которое взят кредит, неизвестно. Пример № 2. 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на (n+1) месяц. Условия его возврата таковы: —1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей. Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей. S = 1000000 рублей = 1000 (тыс. рублей) – сумма кредита, Х = 40 (тыс. рублей) – величина регулярной выплаты, Z = 1378 (тыс. рублей) – общая сумма выплат, Рисуем уже знакомую схему погашения кредита.  Первая выплата: kS – (S – X). Вторая выплата: k (S – X ) – ( S – 2X). … Последняя выплата: k ( S – n X). По условию, 15-го числа n-го месяца долг составит 200 тысяч рублей. Значит, S – nX = 200. Подставим числовые данные: 1000 – 40 n = 200; тогда n = 20, n + 1 = 21, то есть кредит был взят на 21 месяц. Очень удобно – количество месяцев в этой задаче оказалось таким же, как в предыдущей. Поэтому очень кратко повторим основные моменты решения Общая сумма выплат Z: Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – X) = = k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X) = = k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) = = k (21 S – 210X ) – 20 S + 210 k = S (21k – 20) – 210 X (k-1). Мы снова использовали ту же формулу для суммы арифметической прогрессии: По условию, Z = 1378 (тыс. рублей). Выразим k из формулы S (21k – 20) – 210 X (k-1) = Z: Подставим данные из условия задачи. Ответ: r = 3%. Третья задача -та же схема! Пример № 3. 15-го декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы: — 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; — 15-го числа 20-го месяца долг составит 100 тысяч рублей; — к 15-му числу 21-го месяца кредит должен быть полностью погашен. Найдите общую сумму выплат после полного погашения кредита. Тоже задача второго типа – есть информация об уменьшении суммы долга. Точно также будем вести расчеты в тысячах рублей. Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей. S = 300 (тыс. рублей) – сумма кредита, n = 21 – количество месяцев, r = 2%; Х – величина регулярной выплаты, Z – общая сумма выплат. Рисуем ту же схему, что и в предыдущей задаче. По условию, 15-го числа 20-го месяца долг составит 100 тысяч рублей. Значит, S – 20 X = 100. Подставив данные из условия, найдем, что Х = 10. Точно так же считаем сумму выплат (смотри задачи 1 и 2). Z = S (21k – 20) – 210 X (k-1). Подставляем данные из условия: Z = 300 (21 ⋅ 1,02 – 20) – 210 ⋅ 10 ⋅ 0,02 = 384 (тыс. рублей). Ответ: 384000 рублей. Напомним критерии оценивания  Спасибо за внимание! Желаем успехов! | ||||||