тесты физика. Физика тесты. Сборник тестов по курсу общей физики иваново 2006 удк 53 Кудин Л. С. Сборник тестов по курсу общей физики
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯПРИНЯТЫЕ ОБОЗНАЧЕНИЯ A - амплитуда колебания v- скорость A0 - начальная амплитуда x, y - координата, смещение F0 - модуль вынуждающей силы . - амплитуда скорости 0 - амплитуда вынуждающей си- лы g - ускорение свободного паде- ния .. x - ускорение .. xm- амплитуда ускорения
ТЕСТОВЫЕ ЗАДАНИЯКакое из приведенных ниже утверждений есть определение гармониче- ского колебательного движения? а) движение, вызванное внешней периодически изменяющейся силой; б) движение, при котором периодически повторяются значения физических величин, определяющих это движение; в) движение, при котором смещение от положения равновесия со временем меняется по закону синуса или косинуса; г) движение, при котором все точки тела движутся по окружно- стям с центрами, лежащими на одной прямой. Зависимость координаты x от времени t имеет вид: 1) x = 4sin(t - /6); 2) x = А sin2t; 3) x = Аt sint; 4) x = А1 cos(t + ) + А2 cost; 5) x = А sin3t. Какие из зависимостей описывают гармонические коле- бания? а) 1; б) 2, 3; в) 1, 4; г) 3, 4; д) 5. Какой из графиков, приведенных на рисунках, описывает зависимость от времени смещения точки от положения равновесия для гармонического колебательного движения? 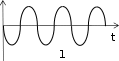  x x x xО О 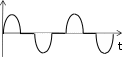 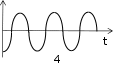 x xО О 3 а) 1; б) 1, 2; в) 2, 3; г) 3, 4; д) 1, 4. Задано уравнение гармонических колебаний: x=Acos(2πt/T+ 0). Какое из нижеприведенных выражений представляет фазу этих колебаний? а) 2πt/T; б) 0; в) 2π/T; г) (2πt/T + 0); д) cos(2πt/T+ 0). Что называется амплитудой гармонических колебаний? смещение тела от положения равновесия в данный момент времени; б) расстояние между точками, колеблющимися в одинаковых фазах; в) расстояние между точками, колеблющимися в противоположных фазах; г) максимальное смещение тела от положения равновесия. Написать уравнение гармонического колебания, если известны его пара- метры: амплитуда колебаний 5 см, циклическая частота 2π с –1, начальная фаза π/4. а) x = 5cos2π/Т(t + π/4); б) x = 5cos2π(t + π/4); в) x = 5cos(2πt + π/4); г) x = 5cos(2πt/T + π/4). Уравнение колебаний имеет вид: x = Аsin(t + ). Какой из приведенных ниже графиков представляет зависимость скорости от времени, при ус- ловии, что = 0.  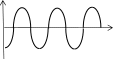 V V V VО t О t 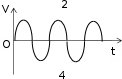 1 1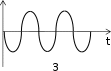 V VО а) 1; б) 2; в) 3; г) 4. Какова начальная фаза гармонического колебания x = Asin( 0t + ), зависи- мость смещения которого от положения равновесия изображена на рисун- ке? 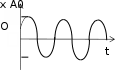 а) 0; б) /2; в) /3; г) /6. Колебательное движение описывается уравнением x = Acos( 0t + ). Ус- тановите соответствие между энергией колебания и ее математическим выражением. Энергия колебаний Математическое выражение а) кинетическая энергия колебаний б) потенциальная энергия колебаний mA2 2  0 1) 2 kA2  2) 4 2) 4mA2 2  в) полная энергия колебаний 3) г) средняя энергия колебаний 2 kA2  0 sin2(0t + ) 2 4) 2 cos (0t + ) а) ; б) ; в) ; г) . Какие из приведенных зависимостей координаты xот времени tне описы- вают гармоническое колебательное движение? 1) x = Аsin(t–/6); 2) x = А1cos(t + ) + А2cost; 3) x = (2Аcos t)cost; 4) x = А cos t + А cos t; 2 5) x = А0e–t·cos(t + ). а) 1; б) 2; в) 3; г) 4; д) 5. 1 1 2 2 Уравнение незатухающих колебаний имеет вид: x = Acos( 0t + ). При- ведите в соответствие закону изменения физической величины от вре- мени математическое выражение. Закон изменения Математическое выражение а) силы 1) – A 2 cos( t + ) 0 0 б) смещения 2) – A0 sin(0t + ) в) скорости 3) Acos(0t + ) г) ускорения 4) – m 2 Acos( t + ) 0 0 а) ; б) ; в) ; г) . Какое из приведенных ниже выражений определяет полную энергию затухающих колебаний? mA2 2  kA2  –2t kA2  –t kA2  а) 2 0 ; б) 2 e ; в) 2 e ; г) 4 . Что обозначает величинаl в выражении периода колебаний физическо- 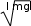 го маятника T= 2 ? го маятника T= 2 ?расстояние от оси вращения до центра тяжести тела; б) приведенную длину физического маятника; в) расстояние от оси вращения до точки качания; г) расстояние между центром тяжести и точкой качания. Из трех гармонических одинаково направленных колебаний с равными амплитудами и частотами, но различными начальными фазами: 1) 2/3, 2) 11/3; 3) 14/3; отобрать пары таких колебаний, которые при сложении гасят друг друга. а) 1 и 2; б) 1 и 3; в) 2 и 3. При какой разности фаз: 1) /3, 2) /2, 3) , 4) /4 в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами получается линейное колебание. а) 1; б) 2; в) 3; г) 4. Какова траектория движения точки, одновременно участвующей в двух взаимно перпендикулярных колебаниях вида: x = Аsint иy =Вcost. а) прямая линия; б) окружность; в) парабола; г) эллипс. Из трех гармонических одинаково направленных колебаний с равными амплитудами и частотами, но различными начальными фазами: 1) /2, 2) 3/2; 3) 5/2 отобрать пары таких колебаний, которые при сло- жении дадут максимальную амплитуду. а) 1 и 2; б) 1 и 3; в) 2 и 3. Установите соответствие между видом колебательного движения и урав- нением, описывающим данный колебательный процесс. Колебательный процесс Уравнение а) свободные незатухающие колебания 1) x = А0e–t·cos(t + ) б) свободные затухающие колебания 2) x = Аcost, y = Вcost в) вынужденные колебания 3) x = Аcos(t +) г) параметрические колебания ⎛ 2 ⎞ 4) x = Аcos ⎜t – arctg 2 – 2⎟ ⎝ 0 ⎠ а) ; б) ; в) ; г) . Какое из приведенных ниже выражений дает значение логарифмическо- го декремента затухания? а) k/m; б) r/2m; в) T; г) 2/; д) t. Для рассматриваемых случаев установите соответствие между периодом и его математическим выражением. Период Математическое выражение а) период колебания математического маятника 1) T =2 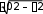 б) период колебания физического маятника 2) T= 2 б) период колебания физического маятника 2) T= 2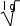 в) период незатухающих колебаний 3) T = 2 в) период незатухающих колебаний 3) T = 2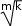 г) период затухающих колебаний 4) T = 2 г) период затухающих колебаний 4) T = 2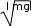 д) период биений 5) T = 2 д) период биений 5) T = 2а) ; б) ; в) ; г) ; д) . Приведите в соответствие колебательным процессам дифференциаль- ные уравнения. Колебательный процесс Дифференциальное уравнение а) незатухающие колебания .. . mx = – kx – rx б) затухающие колебания .. . в) вынужденные колебания mx = – kx – rx + F0cost .. mx = – kx а) ; б) ; в) . Установите правильную последовательность в изменении периода Т для свободных колебаний, совершаемых в среде с коэффициентом за- тухания , равным: 1) = 0, 2) << 0, 3) = 0, 4) > 0. а) T1>T2> T3>T4; б) T1 T2>T3>T4; в) T 1 T2<T3 Приведите в соответствие физические величины их математическим выражениям. Физическая величина Математическое выражение а) декремент затухания 1) m б) время релаксации 2) 2 в) добротность 3) 1 г) коэффициент сопротивления 4) T а) ; б) ; в) ; г) . Установите соответствие между амплитудой и ее математическим вы- ражением. Амплитуда Математическое выражение 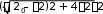 а) незатухающих колебаний 1) A=f0 а) незатухающих колебаний 1) A=f0 б) затухающих колебаний 2) A0e–t., = 0 в) вынужденных колебаний 3) A0e–t., > 0 а) ; б) ; в) . Какое из приведенных ниже выражений определяет резонансную ам- плитуду? а)f0 , б) F0/m, в)f0 , г) f0 . 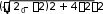 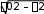 20 20 2 20 20 2Какое из приведенных ниже выражений определяет резонансную часто- ту? 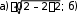 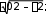 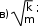 г) 2. г) 2. 0 Уравнение гармонических колебаний имеет вид x = 5cos(πt/4 + π/2) cм. Чему равен период этого колебания? а) 0,25 с; б) π/4 c; в) 1/8 с; г) 4 с; д) 8 с. Система выведена из положения равновесия и предоставлена самой се- бе. Какой будет вид зависимости x = (t) для случая > 0? 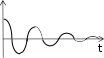   x x x x x xа) б) в) Установите правильную последовательность в изменении для резо- нансных кривых, изображенных на рисунке. 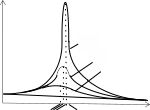 А АF0/k О 1 2 3 рез 0 а) 1 > 2 > 3; б) 1 > 2 < 3; в) 1 < 2 > 3; г) 1 < 2 < 3. Уравнение гармонических колебаний имеет вид x = 0,2cos5t м. Каково амплитудное значение скорости этого тела? а) 0,2 м/с; б) 0,5 м/с; в) 1 м/с; г) 50 м/с; д) 12 м/с. Какую длину должен иметь математический маятник, чтобы период его колебаний был равен 2 с (g = 10 м/с )? а) 0,25 м; б) 0,5 м; в) 1 м; г) 2 м; д) 4 м. Задано уравнение колебанийx=2e -0,1tsin(5πt + π/6)см. Чему равен лога- рифмический декремент затухания? а) 0,04; б) 0,1; в) 0,2; г) 0,5π; д) 10π. A На рисунке представлен график смещения x точки из положения равно- весия в зависимости от времени t. Чему равен логарифм отношения ам- плитуд lnA0 (где N – число полных колебаний). N 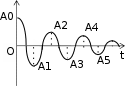 х хN а) T; б) NT; в) T; г) (T)N. |
