Сборник типовых задач содержание введение физические свойства жидкостей 1 Сведения из теории 1 Плотность
 Скачать 0.57 Mb.
|
|
Случай I. В сосудах налита одинаковая жидкость, но давления и различны. тогда при условии, что получим: (2.34) Случай II. Жидкость одинакова, т.е. и . Тогда: (2.35) жидкость в сосудах будет на одном уровне. Случай III. Жидкость одинакова , но один сосуд открыт , а другой закрыт .Тогда: (2.36) (2.37) так как , значит  (2.38)(2.39) Выражение есть пьезометрическая высота для точек, лежащих на поверхности жидкости в закрытом сосуде. Случай IV. Жидкости разнородные, несмешивающиеся, а Тогда: (2.40) или (2.41) Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине 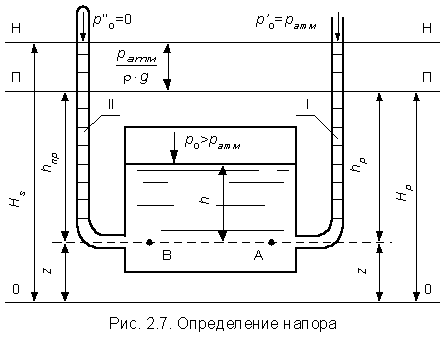 присоединены пьезометры I и II (рис. 2.7). Давление на свободной поверхности в сосуде больше атмосферного . Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному . Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю .Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой . За плоскость сравнения может быть принят уровень земли, пола. Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота. Пьезометрическая высота – мера манометрического давления в точке А. Приведенная высота – мера абсолютного давления в точке В. Разность высот , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст. Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором: . (2.42) Но 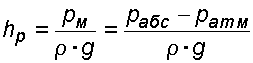 . (2.43)Подставив это выражение в формулу (2.42) получим 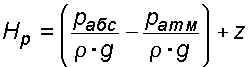 (2..44)или 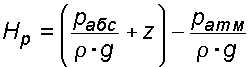 (2.45)это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором . Тогда: (2.46) В уравнении (2.46) для любой точки жидкости, а не зависит от положения точки. Значит: 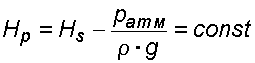 (2.47)Поэтому, сколько бы мы пьезометров не подключили, во всех пьезометрах жидкость установится на одном уровне: плоскость, соответствующая уровню П–П, называется пьезометрической плоскостью, а уровню Н–Н – напорной плоскостью. Пьезометрический напор является мерой удельной потенциальной энергии жидкости. Предположим, что вес частицы жидкости в точке А. равен (рис. 2.7). По отношении к плоскости сравнения О – О запас потенциальной энергии положения равен , где -.высота от плоскости О – О до точки А. Под действием избыточного гидростатического давления частица, находящаяся на глубине , может подняться на высоту ,то есть она обладает потенциальной энергией давления равной . Полная потенциальная энергия частицы жидкости весом равна .Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна: (2.48) Аналогично, гидростатический напор является также мерой удельной потенциальной энергии жидкости, но большей по сравнению на величину удельной потенциальной энергии атмосферного давления. (2.49) 2.2. Примеры решения задач 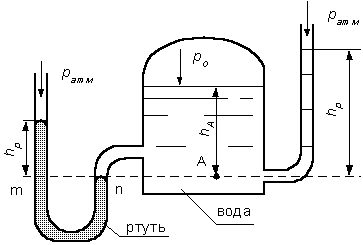 Рис.2.8. Пример 1. Определить абсолютное и избыточное гидростатическое давление в точке А (рис. 2.8), расположенной в воде на глубине , и пьезометрическую высоту для точки А, если абсолютное гидростатическое давление на поверхности . Решение: Согласно основного уравнения гидростатики абсолютное гидростатическое давление в точке А определится: . Избыточное давление в точке А равно:  Пьезометрическая высота для точки А равна:  Можно отметить, что пьезометром удобно измерять только относительно малые давления, в противном случае требуется большая высота пьезометра, что неудобно в эксплуатации. Определить эти же величины U – образным манометром, заполненным ртутью. По поверхности раздела ртути и воды давления со стороны резервуара и открытого конца манометра будут одинаковы:  Следовательно, избыточное давление в точке А уравновешивается весом столба ртути высотой над поверхностью раздела : 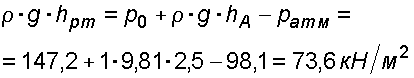 Находим высоту ртутного столба : 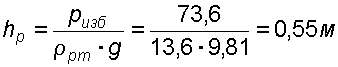 ,где – плотность ртути. 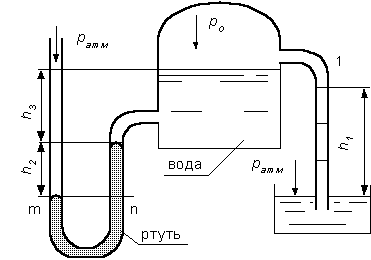 Рис.2.9.Пример 2. Определить давление в резервуаре (рис. 2.9) и высоту подъема уровня в трубке 1, если показания ртутного манометра . Решение: Запишем условия равновесия для ртутного манометра для плоскости а) со стороны резервуара б) со стороны манометра , тогда 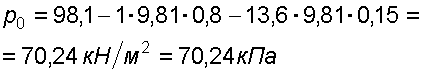  Таким образом, в резервуаре – вакуум, величина которого равна:  Условия равновесия трубки 1 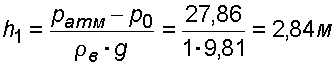 Пример 3. 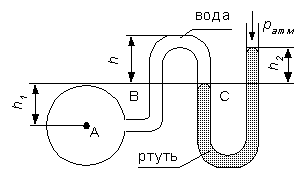 Рис.2.10.Определить манометрическое давление в трубопроводе А (рис. 2.10), если высота столба ртути по пьезометру 25 см. Центр трубопровода расположен на 40 см ниже линии раздела между водой и ртутью. Решение: Находим давление в точке В. Точка В расположена выше точки А на величину , следовательно, давление в точке В будет равно . В точке С давление будет такое же, как в точке В, то есть . Определим давление в точке C, подходя, справа . Приравнивая оба уравнения, получаем  .Отсюда манометрическое давление 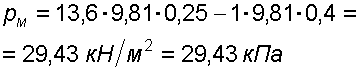 . Пример 4. 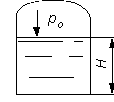 Рис.2.11.Определить все виды гидростатического давления в баке с нефтью на глубине (рис. 2.11), если давление на свободной поверхности нефти . Плотность нефти . Решение: 1. Абсолютное гидростатическое давление у дна 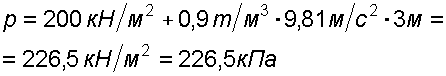 2. Избыточное (манометрическое) давление у дна  3. Избыточное давление создаваемое столбом жидкости  4. Избыточное давление на свободной поверхности  Пример 5. Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра (рис. 2.1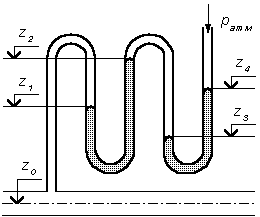2).  Рис.2.12.Отметки уровней ртути от оси трубы: Плотность ртути , плотность воды . Решение: Батарейный ртутный манометр состоит из двух последовательно соединенных ртутных манометров. Давление воды в трубе уравновешивается перепадами уровней ртути, а так же перепадами уровней воды в трубках манометра. Суммируя, показания манометра от открытого конца до присоединения его к трубе получим: 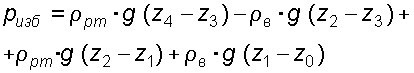 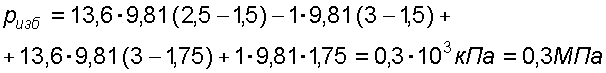 3. ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ 3.1. Сведения из теории Под относительным покоем понимается такое состояние, при котором в движущейся жидкости отдельные частицы не смещаются одна относительно другой. При этом жидкость перемещается как твердое тело. Само движение жидкости в этом случае можно назвать переносным движением. Для этого состояния характерно постоянство формы объема жидкости. Очевидно, что рассматриваемая масса жидкости будет неподвижна в координатной системе, связанной с движущимся резервуаром. На жидкость, находящуюся в относительном покое, действуют массовые силы (силы тяжести и силы инерции переносного движения), а из поверхностных – силы давления. Рассмотрим два частных случая относительного покоя: покой при переносном прямолинейном движении и покой при переносном вращательном движении вокруг вертикальной оси. 3.1.1. Относительный покой при прямолинейном движении на наклонной плоскости Рассмотрим движение резервуара с жидкостью с постоянным ускорением a по наклонной плоскости, образующей угол a с горизонтальной плоскостью (рис. 3.1). 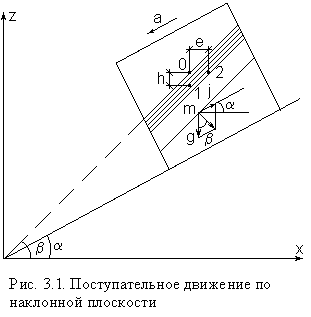 Жидкость в движущемся резервуаре находится под действием силы давления, силы тяжести и силы инерции переносного движения. Ускорение силы инерции и направлено в сторону, обратную ускорению резервуара a. Результирующий вектор массивных сил определяется диагональю параллелограмма, построенного на ускорениях сил тяжести g и инерции j.Элемент поверхности равного давления перпендикулярен к диагонали параллелограмма и образует с горизонтом угол b , тангенс, которого равен (3.1) Таким образом, поверхности равного давления, образуют семейство параллельных плоскостей с углом наклона к горизонту b . Необходимо учесть, что если резервуар движется равномерно , то и следовательно и . В этом случае поверхности равного давления представляют семейство горизонтальных плоскостей. Если резервуар перемещается под действием силы тяжести (сила трения резервуара о плоскость равна 0), то , , , а поверхности равного давления образуют семейство плоскостей, параллельных плоскости скатывания. Если резервуар перемещается с ускорением, но вертикально ( ), то , а поверхности равного давления образуют семейство горизонтальных плоскостей. Найдем закон распределения давления в вертикальной плоскости . Учитывая, что система координат перемещается вместе с резервуаром, , а для выбранной плоскости и , уравнение (2.6) примет вид: . (3.2) В этом случае . Тогда (3.3) После интегрирования имеем: 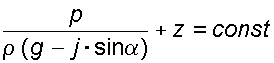 (3.4)Для двух точек 0 и 1 с координатами и имеем: 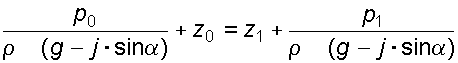 (3.5)или . (3.6) По аналогии получаем распределение давления в горизонтальной плоскости: , (3.7) если , то имеем  , (3.8)а свободная поверхность имеет угол наклона к горизонту (3.1) . (3.9) При свободном падении резервуара и , то есть во всем объеме давление одинаково. 3.1.2 Относительный покой при вращении вокруг вертикальной оси В этом случае на жидкость действуют силы давления, силы тяжести и силы инерции переносного вращательного движения ускорения массовых сил будут равны: Дифференциальное уравнение (2.8) примет вид:  (3.10)После интегрирования, с учетом, что получим: (3.11) 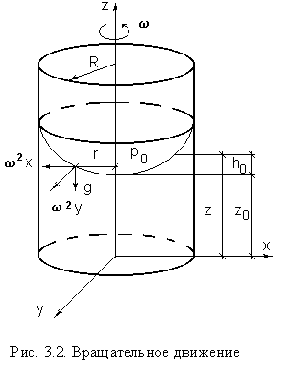 Уравнение (3.11) является уравнением параболоида вращения, а поверхности равного давления образуют семейство параболоидов вращения, сдвинутых вдоль вертикальной оси. Каждый параболоид характеризуется некоторым значением постоянной С. Для параболоида свободной поверхности принимаем, что при (рис. 3.2) , поэтому . Тогда уравнение свободной поверхности примет вид: 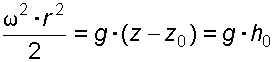 (3.12)или (3.13) Закон распределения давления по объему жидкости получим из уравнения (2.6), подставив в него соответствующие значения X, Y и Z. После интегрирования получаем: 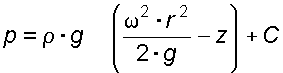 . (3.14)Постоянную интегрирования определим из условия, что при и , т.е. . После подстановки в (3.14) окончательно имеем: 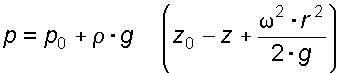 . (3.15)Для частиц жидкости расположенных на одной вертикали можем записать: (3.16) где , т.е. существует обычный гидростатический закон распределения давления. 3.2. Примеры решения задач |