Статика - ИТОГ. Сборник задач по физике. Грабцевич В. И. Сборник задач по физике
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
21. Движение идеальной жидкости 21.1. Насосная станция города поддерживает в водопроводе на уровне первого этажа давление 5 атм. Определите (пренебрегая трением при течении жидкости) скорость струи воды, вытекающей из крана на первом, втором и третьем этажах, если краны каждого последующего этажа расположены на 4 м выше. На какой этаж вода по водопроводу уже не поднимется? [28,0; 27,3; 26,5 м/с. На двенадцатый этаж] 21.2. Сосуд с водой подвешен к потолку. Высота воды в сосуде h. На сколько изменится натяжение подвеса, если в днище сосуда открыть маленькое отверстие, из которого вытекает струя сечения S? Плотность воды . [ 2 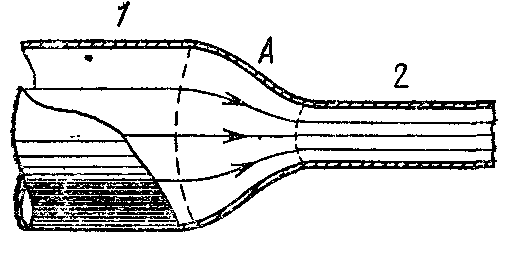 Рис. 21.4 1.3. Насос должен подавать ежесекундно объем Qводы на высоту hпо трубе постоянного сечения S. Какова должна быть мощность насоса? Плотность воды . [ 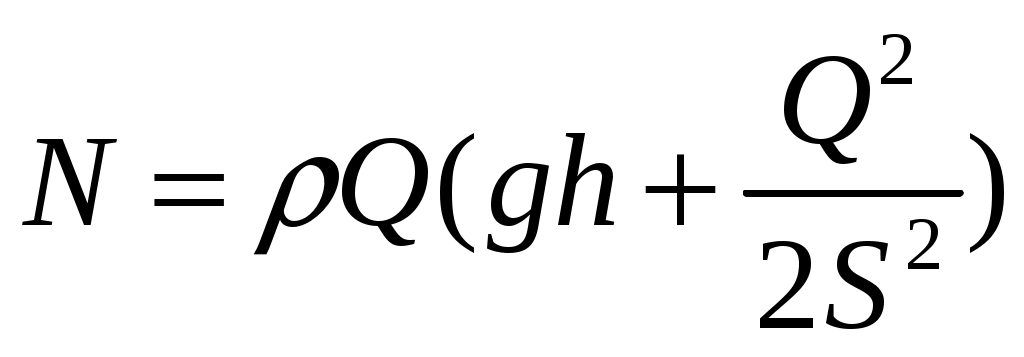 ] ]21.4. а) Стационарный поток жидкости, протекающей по трубе переменного сечения, давит с силой Fна участок Aмежду сечениями 1и 2,который по третьему закону Ньютона давит с такой же силой в противоположном направлении. Следовательно, суммарная сила, действующая на жидкость со стороны этого участка, направлена против движения жидкости. Почему же жидкость в области 2имеет большую скорость, чем в области 1? [а) Из-за разного давления в областях 1 и 2 на жидкость в области между 1 и 2 действует сила давления в направлении движения жидкости. Эта сила больше F] б) Чему равна суммарная сила, действующая на жидкость со стороны участка Л? Площади сечений в областях 1 и 2 равны S1и S2. Плотность жидкости . В области 2 скорость жидкости равна v, давление равно нулю.[б) 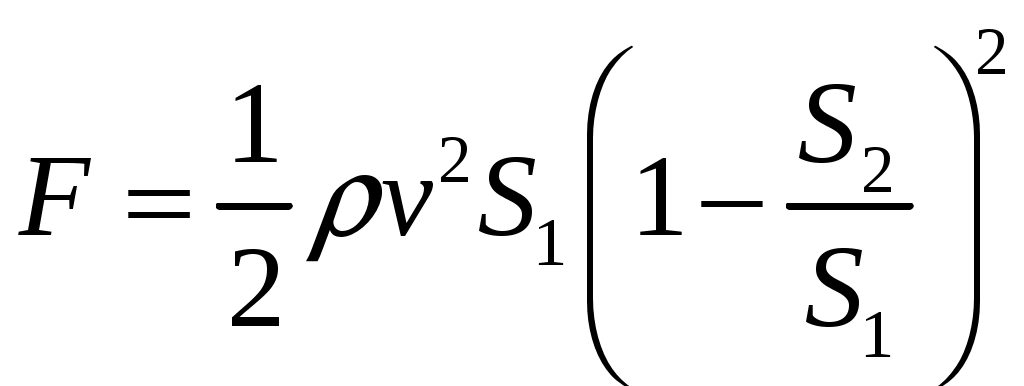 ] ]2 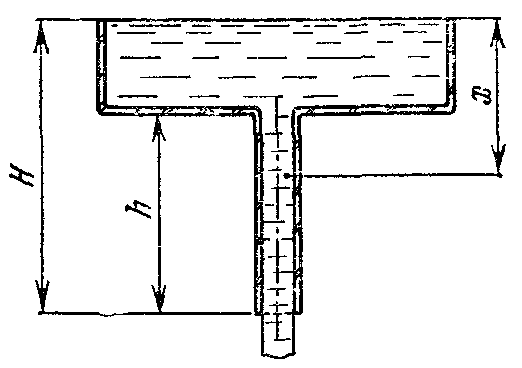 Рис. 21.5 1.5. Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности . Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха Рo. [В сосуде 21.6. По изогнутой под прямым углом трубе поперечного сечения S со скоростью vтечет жидкость плотности . С какой силой жидкость действует на трубу, если давление жидкости на выходе из трубы p? Силой тяжести пренебречь. [ 21.7. Насос представляет собой расположенный горизонтально цилиндр с поршнем площади S и выходным отверстием площади s, расположенным на оси цилиндра. Определите скорость истечения струи из насоса, если поршень под действием силы Fперемещается с постоянной скоростью. Плотность жидкости . [ 21.8. По наклонной плоскости стекает широкий поток воды. На расстоянии l по течению глубина потока уменьшилась вдвое. На каком расстоянии глубина потока уменьшится в 4 раза? [x = 5l] 2 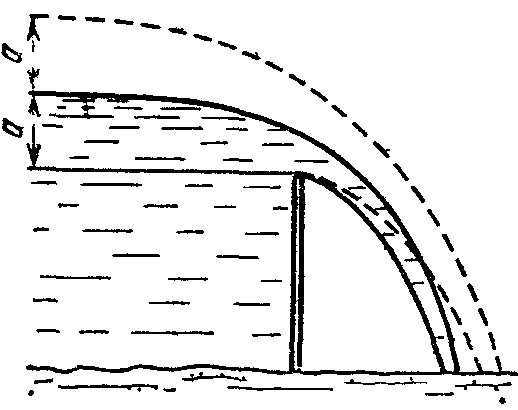 Рис. 21.10 1.9. Плита массы т удерживается на месте в горизонтальном положении N струями жидкости, бьющими вертикально вверх из отверстий сечения S каждое. Скорость жидкости на выходе из отверстий v. На какой высоте над отверстиями удерживается плита? [ 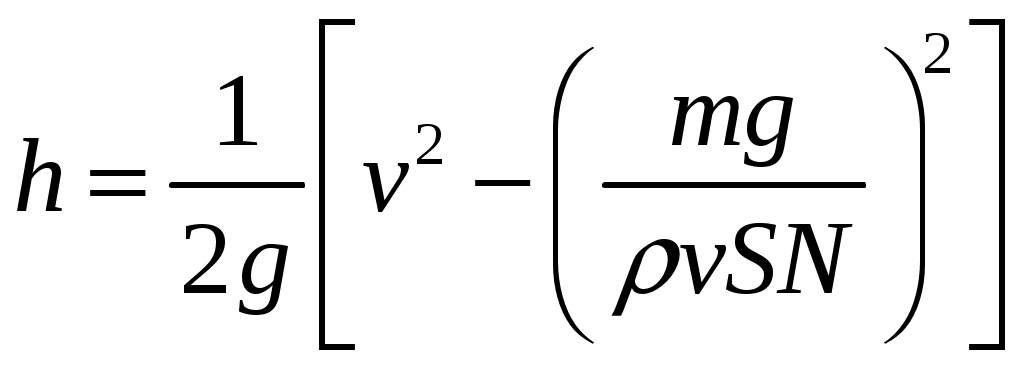 ] ]21.10*. Во сколько раз увеличится сброс воды через широкую плотину, если уровень воды над кромкой плотины возрастет в 2 раза? Профиль плотины изображен на рисунке. [Размеры продольного сечения струи увеличатся в 2 раза. Скорости подобных участков в струе увеличиться в 21.11*. Водосброс из широкого плоского сосуда происходит через треугольный вырез в его кромке. Во сколько раз уменьшится водосброс при понижении уровня воды от H до h? [Струи будут подобны. Размеры струи при понижении уровня воды уменьшатся в H/h раз, Поэтому выброс уменьшится в 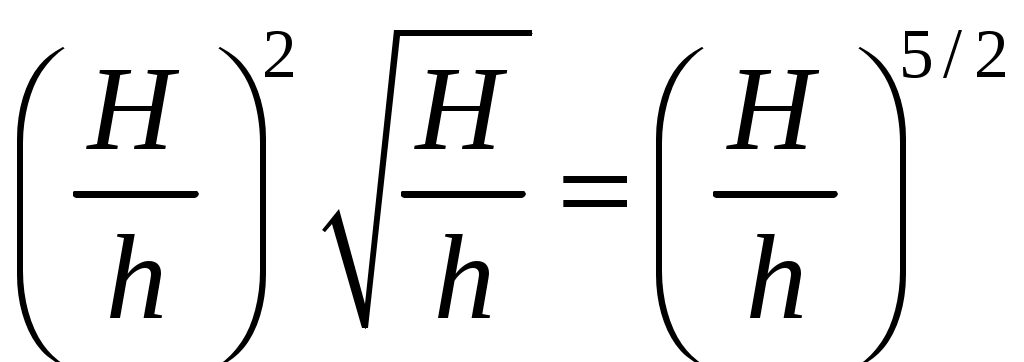 раз.] раз.] 21.12. Плоская бесконечная струя жидкости толщины hпадает под углом со скоростью vна плоскость. На какие струи распадается падающая струя? [На плоскости сохраняется энергия выделенных на рисунке участков струи и их суммарный импульс вдоль плоскости. Из закона сохранения энергии следует, что скорости этих участков на плоскости тоже будут равны v, а из закона сохранения импульса следует, что 2 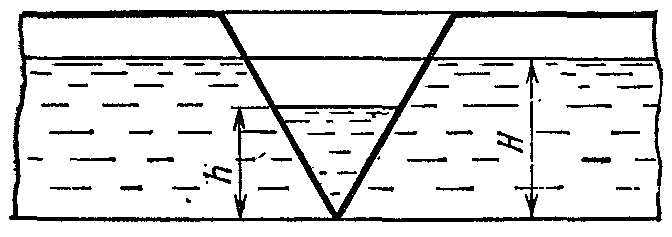 Рис. 21.11 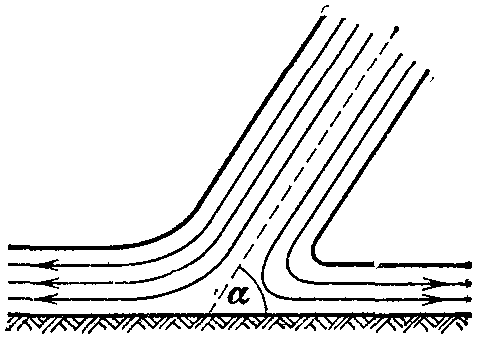 Рис. 21.12 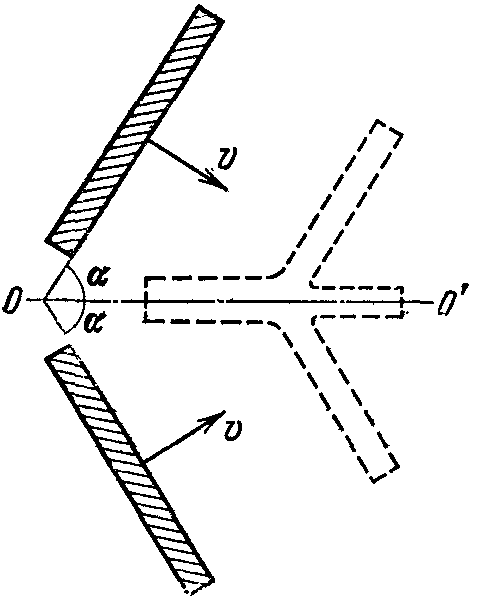 Рис. 21.13 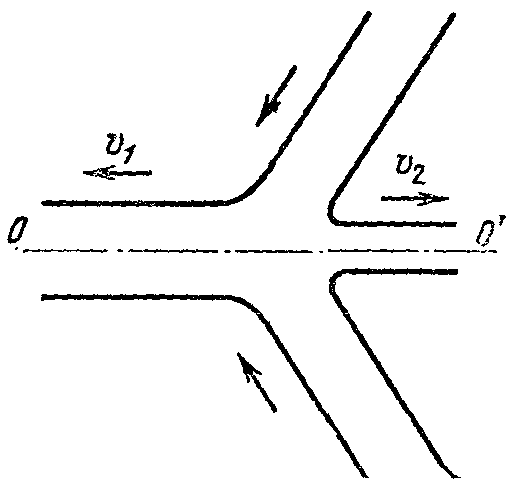 К ответу 21.13 1.13*. Две пластины, расположенные под углом 2 друг к другу, движутся со скоростью v по нормалям к своим поверхностям. Найдите скорости струй, возникающих при столкновении пластин, если движение материала пластин рассматривать как движение идеальной жидкости. [Нужно перейти в систему отсчета, в которой пластины движутся вдоль своих плоскостей. В этой системе материал пластин будет двигаться как две встречные струи, изображенные на рисунке. Их движение над и под плоскостью OO/ повторяет движение струи, рассмотренной в задаче выше: 21.14*. Определите форму стационарной струи после столкновения двух струй радиусов Rи r, которые двигались навстречу друг другу с одинаковыми скоростями. [Конус с 2  Рис. 21.15 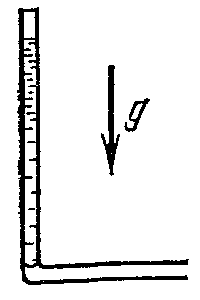 Рис. 3.16 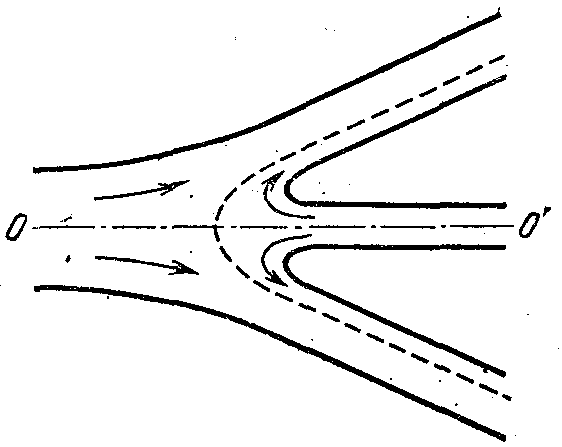 К ответу 21.14 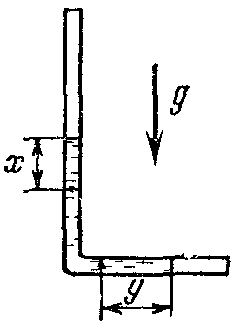 К ответу 21.16 1.15. «... В 1941 году немцы придумали кумулятивный противотанковый снаряд. На конусе снаряда – запал. При ударе он вызывает детонацию и воспламеняет весь заряд. Снаряд пробивает всю броню. В 1944 году такие немецкие снаряды попали в наши руки и руки союзников. Начался широкий эксперимент. При этом обнаружили много дополнительных эффектов и парадоксов. Стали выяснять – что же летит, что пробивает? Сперва думали, что этот снаряд бронепрожигающий, что броню пронзает струя горячего газа. Нет, оказалось, что летит металл...: перед плитой со скоростью 8 км/с, внутри плиты 4 км/с, за плитой снова 8 км/с»(Из вступительного слова председателя Президиума СО АН СССР академика М. А. Лаврентьева перед учащимися Летней физико-математической школы в 1971 году). Объясните это явление. Определите, с какой скоростью двигалась стенка металлической конической полости, перекрывающей заряд, если угол при вершине полости 30°. [Необходимо перейти в систему отсчета, в которой встречные скорости брони и струи металла будут равны по модулю. vc = 1 км/с] 21.16*. Плотность жидкости . В начальный момент она заполняет вертикальный участок длины lв тонкой L-образной трубке. Найдите, как зависит от времени высота уровня жидкости. Найдите распределение давления в момент, когда высота столба уменьшится наполовину. [ 21.17*. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S,сечение струи s. Уровень воды сосуде перемещается с постоянным ускорением. Найдите это ускорение. [ 21.18. В цилиндре с поршнем находится вода, внутри которой в начальный момент имеется полость объема V. Поршень оказывает на воду постоянное давление p. Какую энергию приобретет вода в момент, когда полость исчезнет? [ 21.19*. Рассмотрите «замыкание» сферической полости в большом водоеме. Давление воды p,начальный радиус полости R. Определите скорость воды на границе полости в момент, когда ее радиус был равен r. [ 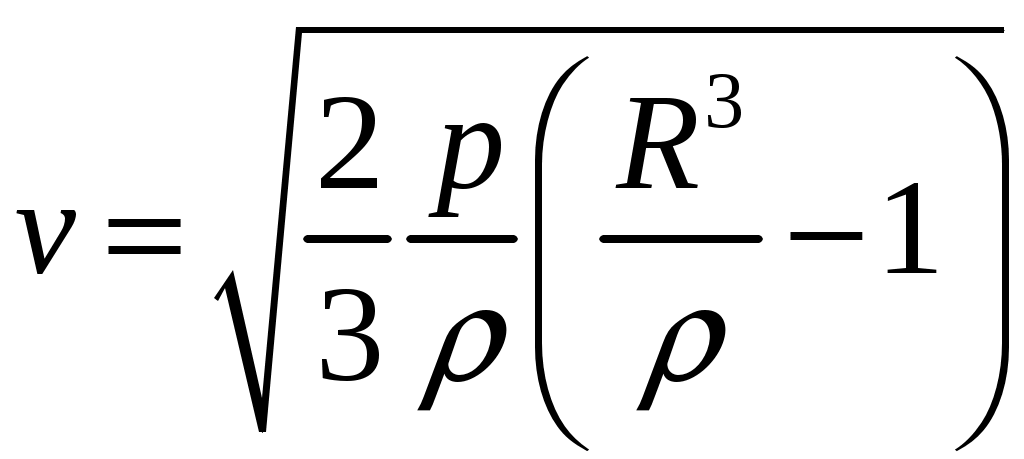 ] ]21.20. а) Оцените, при какой скорости кромки лопасти винта катера за лопастью возникнет полость. [При скорости, большей 14 м/с] б*) При какой интенсивности ультразвука в воде при атмосферном давлении начнут появляться микрополости? Сжимаемость воды 510–10 Па–1. [При интенсивности, большей 700 Вт/м2] 22. Течение вязкой жидкости 22.1. Пространство между двумя параллельными плоскостями заполнено жидкостью вязкости . Одна из плоскостей движется со скоростью vo,другая покоится. Найдите распределение скоростей жидкости между плоскостями и силу вязкости, действующую на единицу площади каждой из плоскостей. Расстояние между плоскостями h. [ 22.2. Найдите распределение скоростей при установившемся течении жидкости между двумя плоскостями. Расстояние между плоскостями h,вязкость жидкости . Найдите расход жидкости на единицу ширины потока, если перепад давления на единицу длины (в направлении движения жидкости) равен p. [ 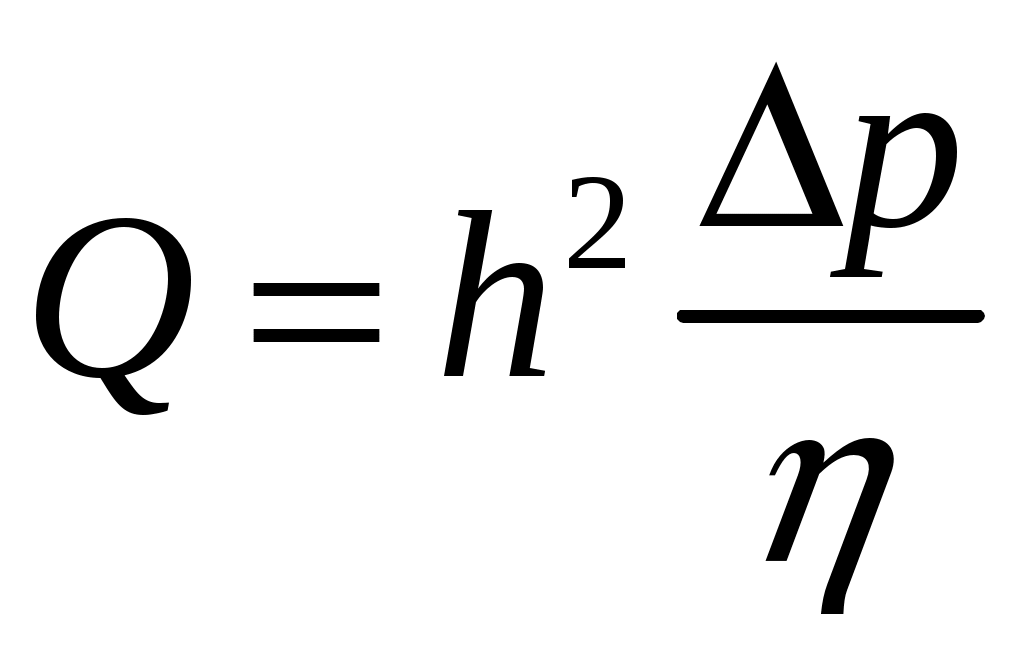 ] ]22.3*. Жидкость перекачивается из одного сосуда в другой через длинную трубку радиуса Rи длины l. Определите зависимость скорости жидкости от расстояния до стенки трубки, если разность давлений на концах трубки p, вязкость жидкости . [ 22.4. Определите расход жидкости на единицу ширины плоского потока, стекающего по наклонной плоскости под углом к горизонту. Вязкость и плотность жидкости и . Толщина потока h. [ 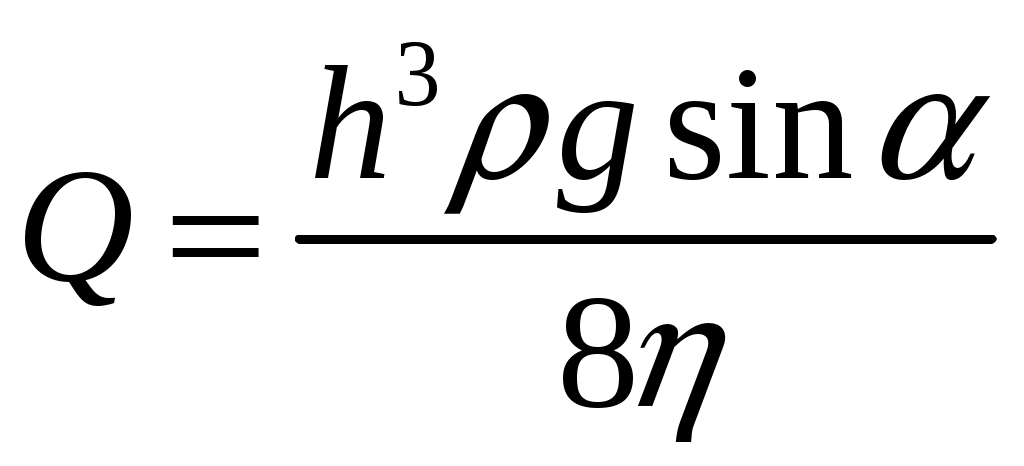 ] ]23. Механика твердого тела. Момент импульса 23.1. Легкая металлическая бочка, полностью заполненная водой, скатывается без проскальзывания с наклонной плоскости. Как изменится ускорение бочки, если вода замерзнет? 23.2. Тонкий обруч раскрутили до угловой скорости и вертикально поставили на горизонтальную поверхность. Какая угловая скорость будет у обруча в установившемся движении? 23.3. Чему равна кинетическая энергия тонкого обруча массой m, катящегося по горизонтальной поверхности со скоростью v? 23.4. Тонкий обруч скатывается без проскальзывания с наклонной плоскости с углом наклона . Найти ускорение центра обруча. Каким должен быть коэффициент трения, чтобы не было проскальзывания? 23.5. Тонкий обруч радиусом R раскрутили до угловой скорости и плашмя положили на стол. Через время t обруч остановился. Определить коэффициент трения между обручем и столом. 23.6. Два маленьких шарика массами m1 и m2 находятся на расстоянии l друг от друга. Определить момент инерции системы относительно ее центра масс. 23.7. Определить момент инерции однородного стержня относительно оси, проходящей через середину стержня и составляющей угол со стержнем. Длина стержня равна l, его масса – m. 2 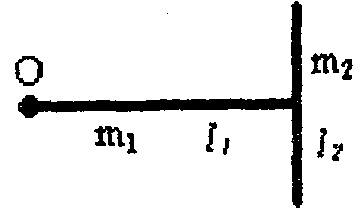 Рис. 1 3.8. Прямоугольник со сторонами aи bсделан из однородной проволоки. Масса единицы длины проволоки равна . Определить момент инерции прямоугольника относительно оси, совпадающей со стороной, длина которой равна а. 23.9. Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m1 и т2и длиной l1 и l2. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы (рис. 23.1). 2 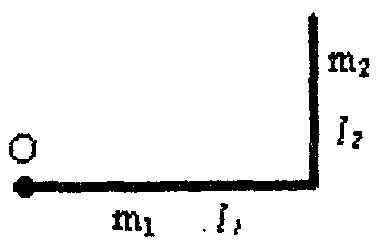 Рис. 2 3.10. Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m1 и m2 и длиной l1 и l2. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы (рис. 23.2). 23.11. Из однородного диска радиусом R вырезано круглое отверстие радиусом r. Расстояние между центрами диска и отверстия равно а,а масса фигуры – m. Определить момент инерции фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости. 23.12. Из однородной проволоки сделан правильный треугольник. Масса стороны треугольника равна m, его длина равна l. Определить момент инерции треугольника относительно оси: а) проходящей через центр треугольника и перпендикулярной его плоскости; б) совпадающей с од ной из сторон треугольника; в) проходящей через вершину и параллельной противоположной стороне треугольника. 23.13. Однородный шар скатывается с наклонной плоскости с углом наклона а. Найти ускорение центра шара. Каким должен быть коэффициент трения, чтобы шар не скользил? 2 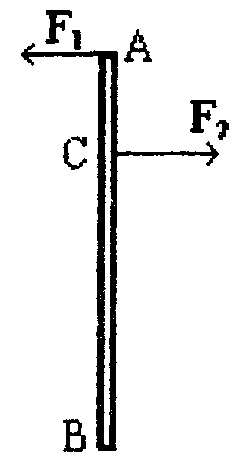 Рис. 3 3.14. В вагоне, движущемся с постоянной скоростью v, к потолку шарнирно подвешен стержень длиной l. На какой максимальный угол от вертикали отклонится стержень, если вагон резко остановить? 23.15. Однородный тонкий стержень длиной l поставили вертикально на горизонтальную гладкую поверхность, слегка вывели из положения равновесия и отпустили. Какую скорость будет иметь верхний конец стержня в момент удара стержня о поверхность? 23.16. Тонкий стержень AB массой m = 1 кг движется поступательно с ускорением a = 1м/с2 под действием двух сил F1 и F2 (рис. 23.3). Расстояние между точками приложения сил АС = 20 см. Сила F2 = 5 Н. Найти длину стержня. 2 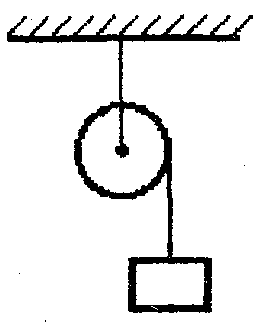 Рис. 4 3.17. Неподвижный блок представляет собой однородный цилиндр массой m, подвешенный на нити к потолку. На цилиндр намотана нить, к которой подвешен груз такой же массы m (рис. 12.4). Найти силу натяжения верхней нити при свободном движении системы. Трения нет. |
