Статика - ИТОГ. Сборник задач по физике. Грабцевич В. И. Сборник задач по физике

• Название: Сборник задач по физике. Грабцевич В. И. Сборник задач по физике
• Дата: 16.03.2022
• Размер: 1.12 Mb.
• Имя файла: Статика - ИТОГ.doc
• Тип: Сборник задач; #399555
• страница: 4 из 6

18.50. Воздушный шар опускается с постоянной скоростью. Общая масса оболочки и груза равна М, объем оболочки – V, плотность воздуха – _в, плотность газа в оболочке – . Какой массы груз надо выбросить, чтобы шар начал подниматься с той же постоянной скоростью? Считать, что сила сопротивления пропорциональна скорости. [ ]

1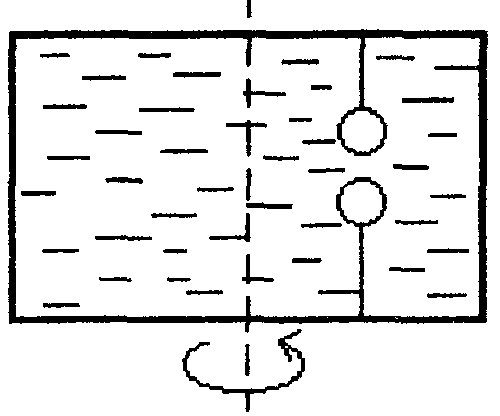


Рис. 17
8.51. В вертикальном цилиндрическом сосуде, доверху заполненном водой и закрытом крышкой, на нитях висят два шарика: сверху стальной; снизу пробковый (рис. 17). Как будут вести себя шарики, если сосуд начнут медленно раскручивать вокруг его оси? [верхний шарик будет отклоняться от оси, а нижний – к оси]

1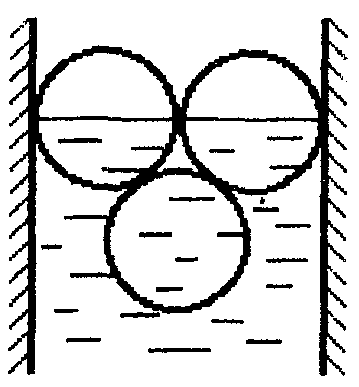


Рис. 18
8.52. Три одинаковых бревна плавают в воде между вертикальными стенками канала. Расстояние между стенками слегка больше удвоенного диаметра бревен, а верхние бревна погружены в воду ровно наполовину (рис. 18). С какой силой бревна давят на стенки канала, если масса каждого бревна равна m? Трения нет. [ ]

18.53. Большая плоская льдина плавает в воде. В льдине просверлили прорубь площадью S = 300 см². Вода в проруби оказалась на глубине h = 10 см. Какое максимальное количество масла можно налить в прорубь? Плотность масла равна _м = 800 кг/м³. [ 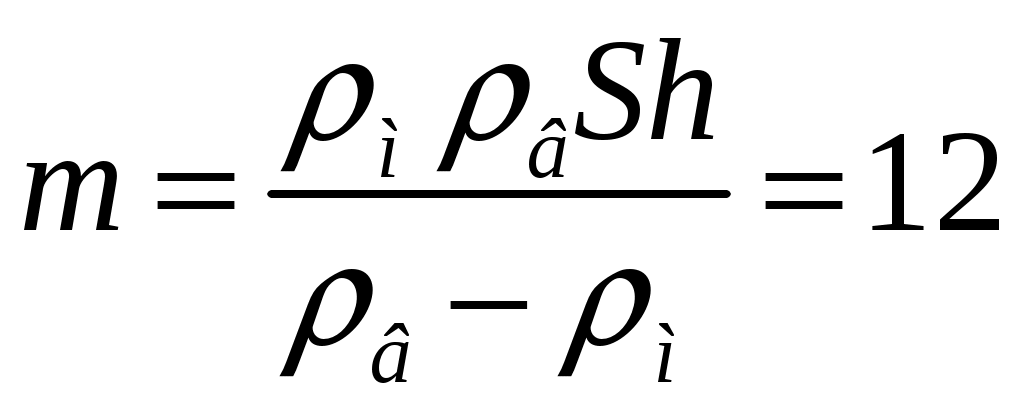кг]

1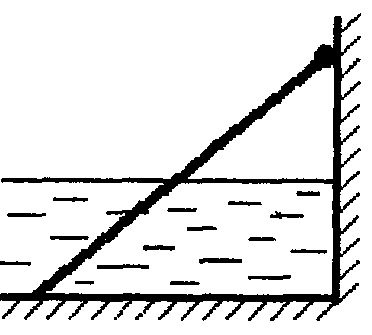


Рис. 19
8.54. Два шарика, сделанные из одного материала, имеют объемы: V и 3V. Шарики связали невесомой нитью, перекинутой через неподвижный блок, и отпустили над поверхностью воды. Когда один из шариков погрузился в воду ускорение системы изменилось на противоположное. Найти плотность материала шариков. Сопротивление воды и трение не учитывать. [ кг/м³]

18.55. Тело массой m тонет в воде с ускорением a. С какой силой его надо тянуть вверх, чтобы оно поднималось с тем же ускорением? Сопротивление не учитывать. [ ]

18.56. Тонкий однородный стержень длиной l = 1 м, сделанный из материала с плотностью  = 0,91 г/см³, шарнирно прикреплен к стенке бассейна и опирается на дно так, что составляет угол  = 60° с вертикалью (рис. 19). В бассейн начинают наливать воду. При какой высоте уровня воды стержень перестанет давить на дно? [ 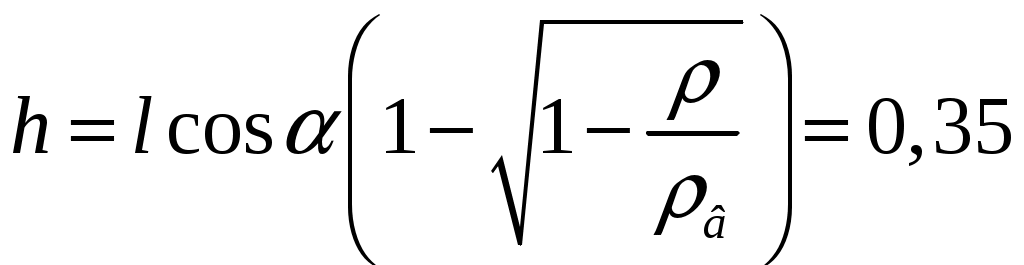м]

18.57. Цилиндрический сосуд радиусом R, заполненный жидкостью с плотностью , вращается вокруг своей вертикальной оси с угловой скоростью . В сосуде находится маленький шарик радиусом r и плотностью 2 (r << R). С какой силой шарик давит на боковую поверхность сосуда? [ ]

18.58. Аквариум с водой на колесиках скатывается с наклонной плоскости без трения. Как располагается уровень поверхности воды при установившемся скатывании? [Параллельно наклонной плоскости]
19. Давление в жидкости.

1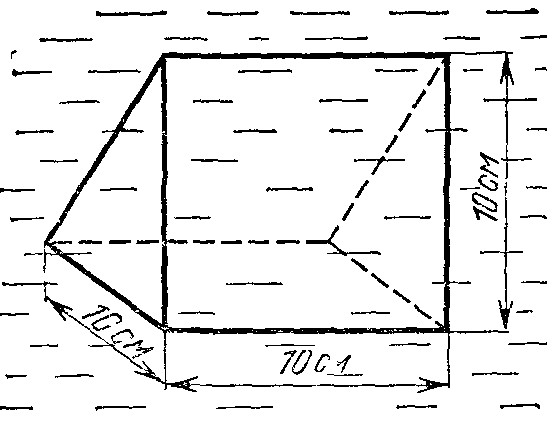


Рис. 19.1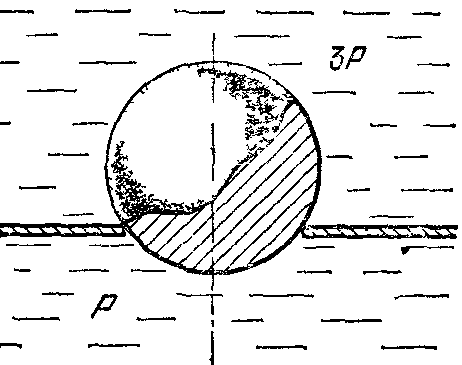




Рис. 19.4
9.1. В жидкости находится прямоугольная призма, размеры которой показаны на рисунке. Найдите сумму сил, действующих на переднюю и нижнюю грань призмы, если давление жидкости 210⁵ Па. Чему равна сумма сил, действующих на призму? [ H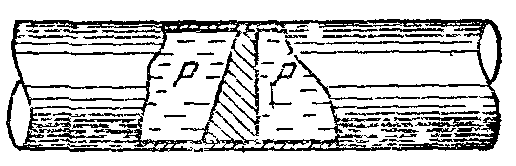. Нуль]

1


Рис. 19.3
9.2. Результирующая сила, действующая со стороны сжатой жидкости на три грани правильного тетраэдра, равна F. Длина ребра тетраэдра а. Определите давление жидкости. [ ]

19.3. В трубе находится поршень, продольное сечение которого показано на рисунке. Давление жидкости с обеих сторон поршня одинаково. Находится ли поршень в равновесии? [Да]

1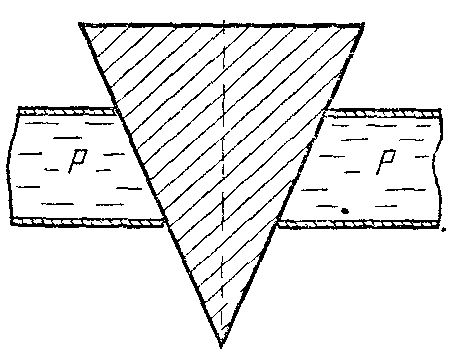


Рис. 19.5
9.4. Шар перекрывает отверстие радиуса rв плоской стенке, разделяющей жидкости с давлениями 3P и Р. С какой силой прижимается шар к отверстию? [ ]

19.5. Коническая пробка перекрывает сразу два отверстия в плоском сосуде, заполненном жидкостью при давлении Р. Радиусы отверстий rи R. Определите силу, действующую на пробку со стороны жидкости. [ ]

19.6*. Сферический баллон радиуса Rсо стенками толщины  << Rразрывается внутренним давлением Р. Определите предел прочности материала стенок. [ ]

1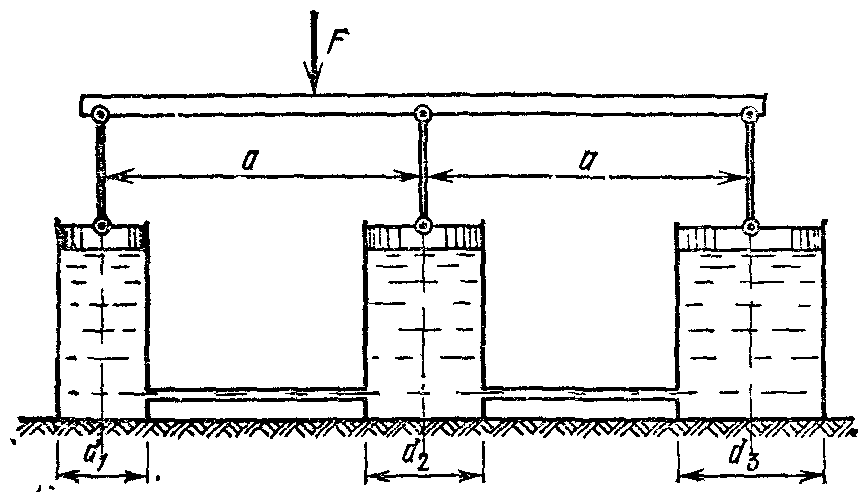


Рис. 19.8
9.7. Почему сосиска в кипятке лопается вдоль, а не поперек? [Сила F₁, действующая на единицу длины периметра поперечного сечения сосиски, меньше силы F₂, действующей на единицу длины периметра продольного сечения сосиски.]

19.8. Три сообщающихся сосуда с водой прикрыты поршнями. К поршням шарнирно прикреплена на вертикальных стержнях горизонтальная палка. В каком месте нужно приложить к палке силу F,чтобы палка осталась горизонтальной? Диаметры сосудов и расстояния между ними указаны на рисунке. [ 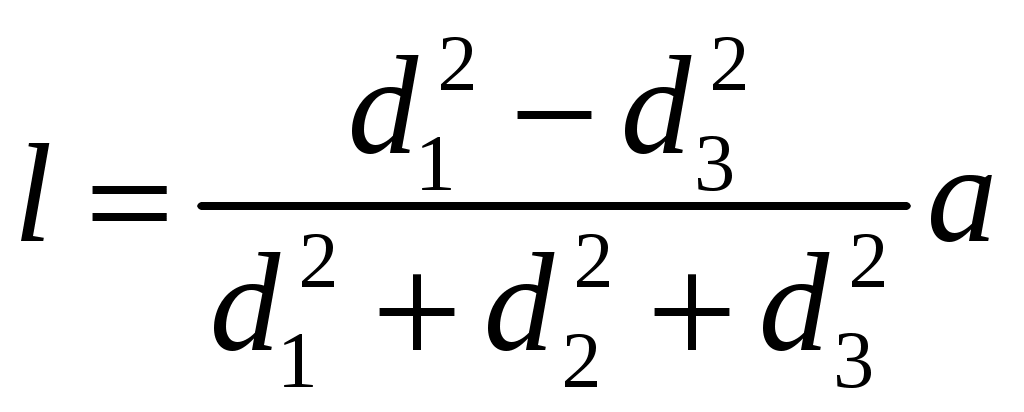от центра палки]

19.9. Гидравлический пресс, заполненный водой, имеет поршни сечений 100 и 10 см². На большой поршень становится человек массы 80 кг. На какую высоту поднимется после этого малый поршень? [h = 727 см]

1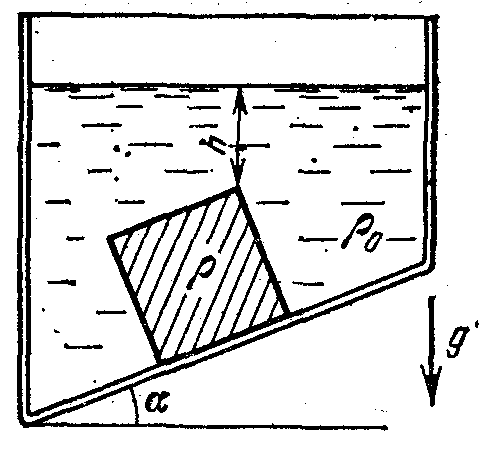


Рис. 19.12
9.10. Тело в форме куба, ребро которого 20 см, находится в воде. Нижняя грань куба удалена от поверхности воды на расстояние 1 м. Чему равна сила, действующая со стороны воды на нижнюю грань? Верхнюю грань? Какая сила действует на боковую грань куба? Найдите векторную сумму сил, действующих на тело. [F_н = 392 H, F_в = 314 H, F_б = 353 H, F = 78 H]

19.11*. Нижняя грань правильного тетраэдра с ребром а, полностью погруженного в жидкость плотности , удалена на расстояние hот поверхности жидкости. Определите силу, действующую со стороны жидкости на боковую грань тетраэдра. Ускорение свободного падения g.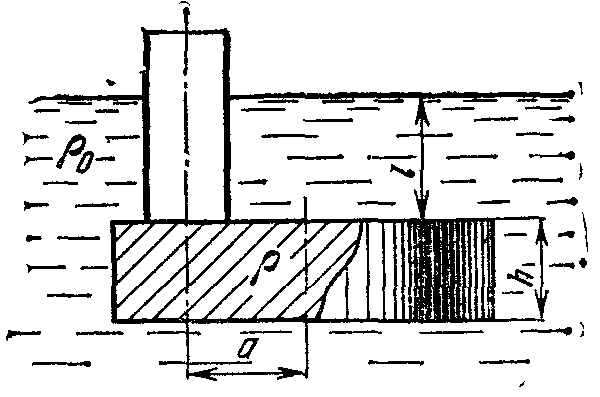

[


Рис. 19.13
]

1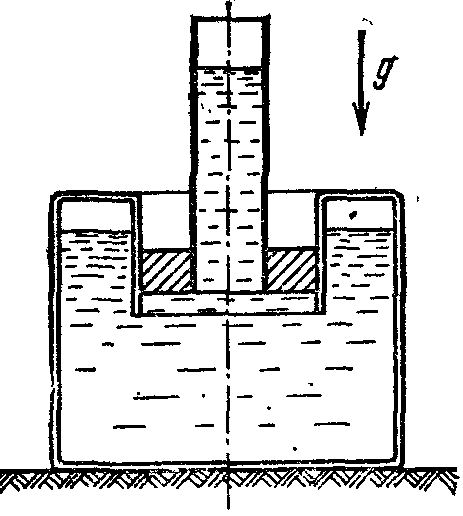


Рис. 19.14
9.12. На дне сосуда, которое составляет угол  с горизонтом, стоит куб с ребром а,сделанный из материала плотности . Найдите силу, с которой куб действует на дно, если в сосуд налита жидкость плотности _o. Верхнее ребро куба находится на расстоянии hот поверхности жидкости. Между дном сосуда и кубом жидкости нет. [Составляющие силы, параллельная и перпендикулярная дну: , ]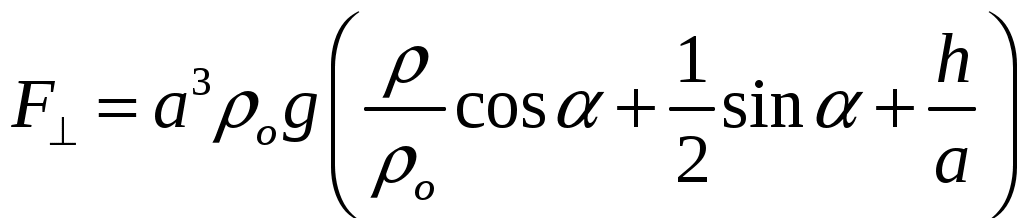

19.13. Трубка радиуса rзакрыта снизу металлическим диском и погружена в жидкость на глубину l. Радиус диска R,высота h. Ось диска отстоит от оси трубки на расстоянии а. Плотность жидкости _o, плотность металла . До какой высоты нужно наливать жидкость в трубку, чтобы диск оторвался от трубки? [ ]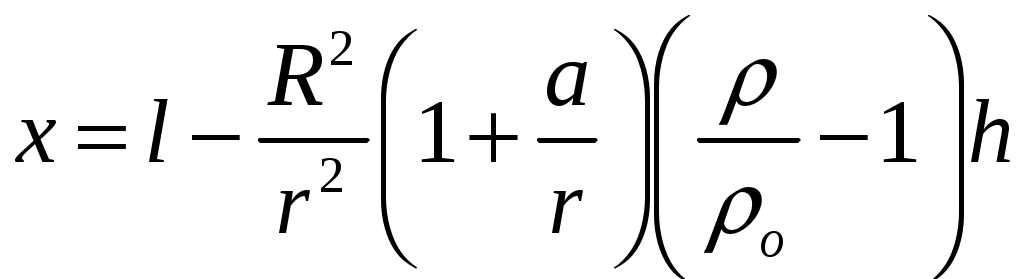

19.14. В крышке сосуда с водой имеется цилиндрическое отверстие, плотно закрытое подвижным поршнем. В поршень вделана вертикальная трубка. Радиус поршня 50 см, радиус трубки 5 см, масса поршня вместе с трубкой 20 кг. Определите высоту столба воды в трубке при равновесии системы. [h = 85 см]

1


Рис. 19.16
9.15. Поршень, перекрывающий цилиндрическую трубку внутреннего радиуса 10 см, может перемещаться с помощью длинного вертикального штока. Трубка с поршнем, занимающим крайнее нижнее положение, опущена в цилиндрический колодец радиуса 1 м на глубину 0,5 м. На какую высоту от первон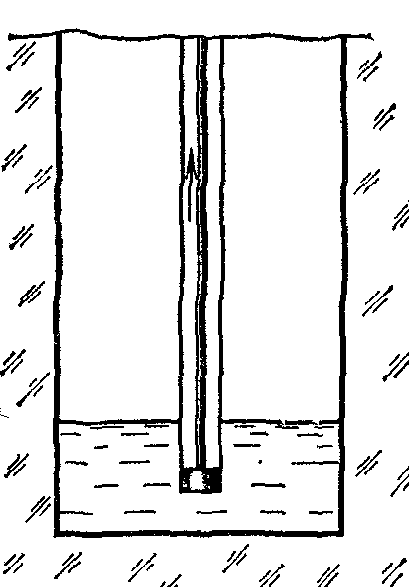


Рис. 19.15

ач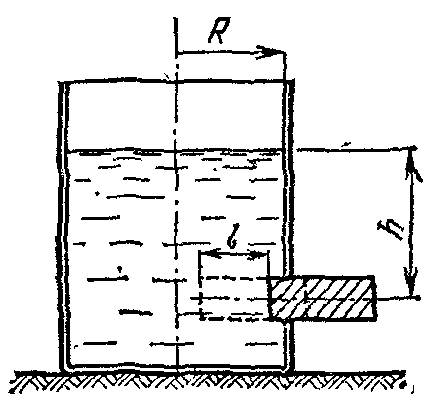


Рис. 19.18

ального уровня воды в колодце можно поднять воду в трубке? Атмосферное давление 10⁵ Па. [h = 10,1 м]

19.16*. В полусферический колокол, плотно лежащий на столе, наливают через отверстие вверху жидкость. Когда жидкость доходит до отверстия, она приподнимает колокол и начинает вытекать снизу. Найдите массу колокола, если его внутренний радиус равен R,а плотность жидкости . [ ]

19.17. Докажите, что в двух сообщающихся сосудах Жидкость в поле тяжести имеет минимальную потенциальную энергию, когда уровни жидкости в обоих сосудах совпадают.

1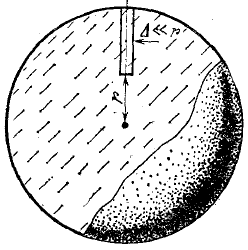


Рис. 19.20
9.18*. В цилиндрическом сосуде радиуса R,наполненном жидкостью плотности , в боковой стенке имеется отверстие, заткнутое пробкой. Какую работу нужно совершить, чтобы вдвинуть пробку на длину l?Пробка имеет вид цилиндра радиуса r.Центр отверстия находится на глубине h. Сосуд достаточно высок, чтобы вода из него не выливалась. Трение не учитывать. [ ]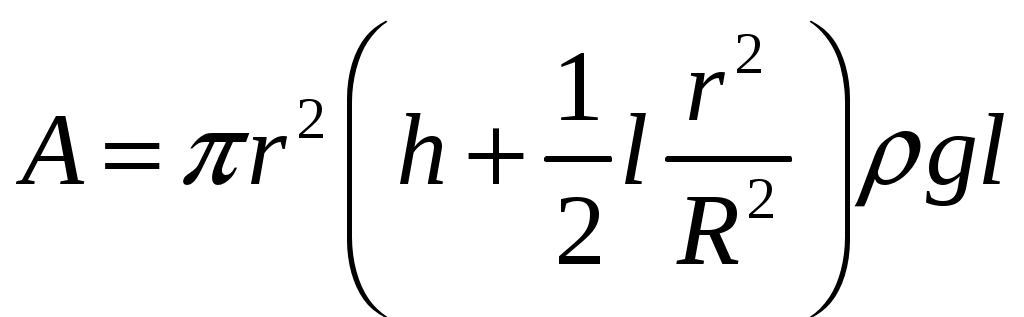

19.19*. Найдите давление на расстоянии r от центра жидкой планеты радиуса R, если жидкость имеет плотность . Чему равно давление в центре планеты? Гравитационная постоянная G. [Давление p_r можно найти из условия равновесия выделенного на рисунке тонкого цилиндрического объема: сила притяжения этого объема жидкости к центру планеты равна силе давления, действующей на нижнее сечение объема. ]

19.20. В сосуде с жидкостью находится газовый пузырь. Поля тяжести нет. Сосуд начинает двигаться с постоянным ускорением. Куда начнет двигаться пузырь? [В направлении вектора ускорения]

19.21. Под каким углом к горизонту расположится поверхность жидкости в сосуде, скользящем по наклонной плоскости, составляющей угол  с горизонтом? Коэффициент трения . [ ]

1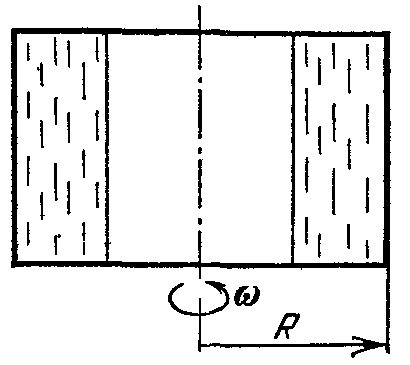


Рис. 19.23
9.22*. Закрытый цилиндр радиуса R, заполненный на 3/4 своего объема жидкостью плотности , вращается в невесомости вместе с жидкостью с угловой скоростью  вокруг своей оси. Как меняется давление в жидкости в зависимости от расстояния до стенок цилиндра? [Давление p(x) можно найти из условия, что сила давления на внутреннее сечение выделенного на рисунке тонкого цилиндрического объема равна , г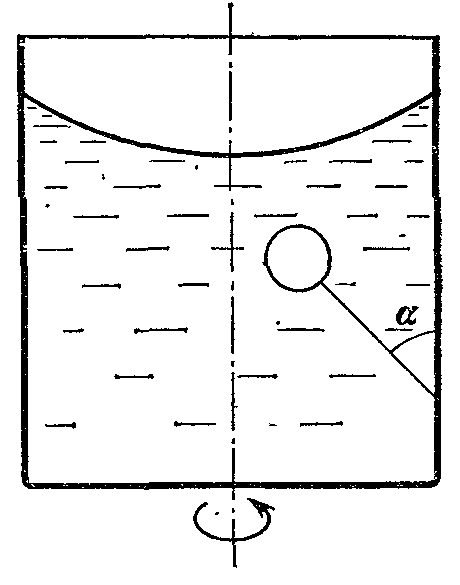де y – расстояние от центра цилиндра до оси вращения, m – масса выделенного объема. Ответ: ]
1


К задаче 19.23
9.23. Найдите форму поверхности жидкости в вертикально расположенном цилиндрическом стакане, который вращается вокруг своей оси с угловой скоростью . Ускорение свободного падения g. [ ]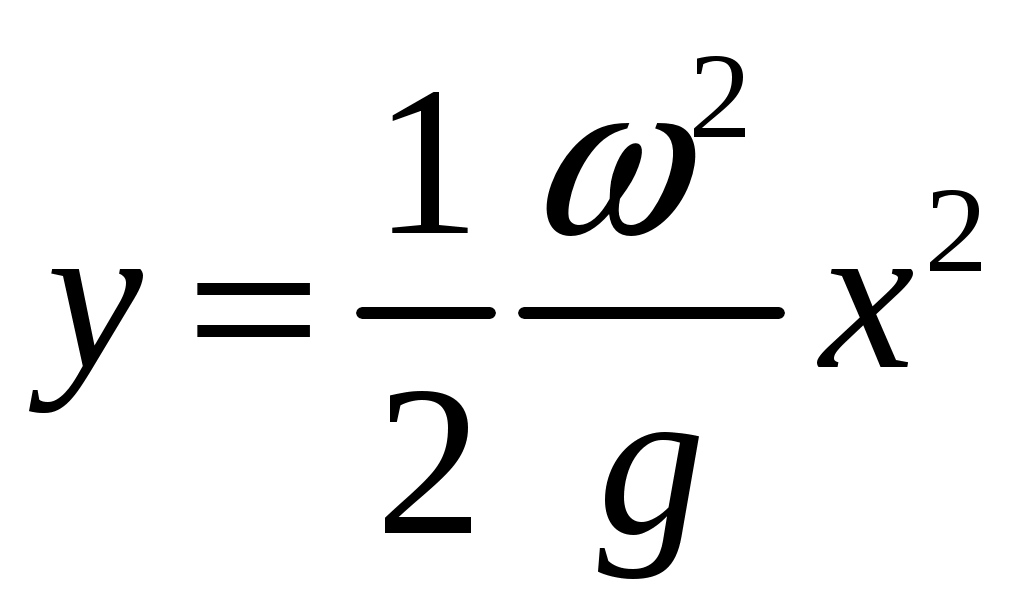

20. Плавание. Закон Архимеда

20.1. Определите давление жидкости на нижнюю поверхность плавающей шайбы сечения S и массы m. [ ]

2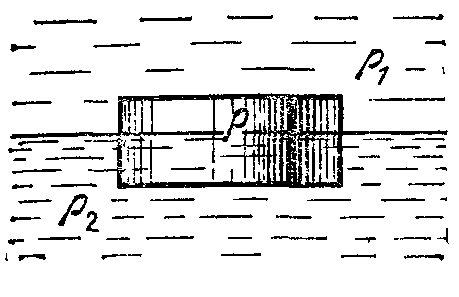


Рис. 20.2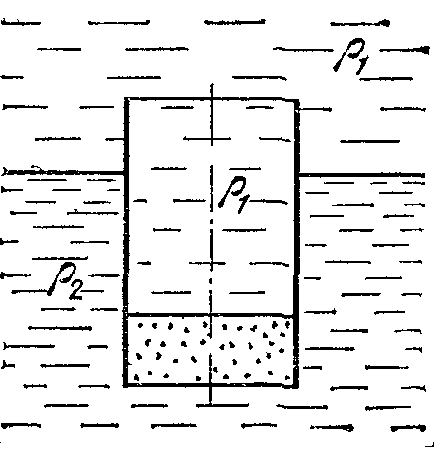




Рис. 20.3

0.2. На границе раздела двух жидкостей плотностей ₁ и ₂ плавает шайба плотности  (₁ <  < ₂). Высота шайбы h. Определите глубину ее погружения во вторую жидкость. [ x = h(₁)/(₂ ₁). Ответ исправлен 19.11.2010]

20.3. Тонкостенный стакан массы т вертикально плавает на границе раздела жидкостей плотностей ₁ и ₂. Определите глубину погружения стакана в нижнюю жидкость, если дно стакана имеет толщину hи площадь S и стакан заполнен жидкостью плотности _l. [ ]

20.4*. В жидкости плотности _o плавает прямоугольный параллелепипед из мат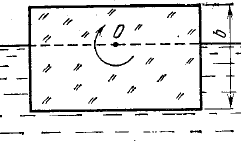


К задаче 20.4
ериала плотности . Высота параллелепипеда b, ширина и длина a. При каком отношении aк bего положение устойчиво? [Если при повороте параллелепипеда вокруг оси, проходящей через точку O, центр тяжести системы жидкость – параллелепипед повышается, положение параллелепипеда устойчиво. Это условие выполняется при ]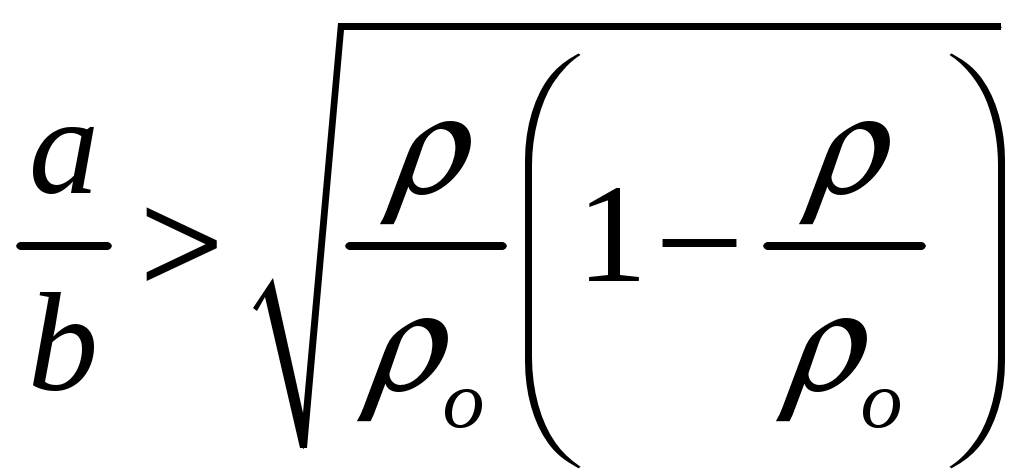

20.5. Деревянный куб с ребром 0,5 м плавает в озере, на ²/₃ погруженный в воду. Какую минимальную работу нужно совершить, чтобы утопить куб? [A = 32,5 Дж]

20.6. Кусок железа весит в воде 1 H. Определите его объем. Плотность железа 7,8 г/см³. [V = 147 см³]

20.7. Тело в воде весит в три раза меньше, чем в воздухе. Чему равна плотность тела? [ = 1,5 г/см³]

20.8. К коромыслу весов подвешены два груза равной массы. Если один из грузов поместить в жидкость плотности ₁, а другой в жидкость плотности ₂, то равновесие сохранится. Найдите отношение плотностей грузов. [ ]

20.9*. В сообщающиеся сосуды диаметров d₁и d₂налита жидкость плотности . На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы mиз материала, плотность которого меньше ? [ ]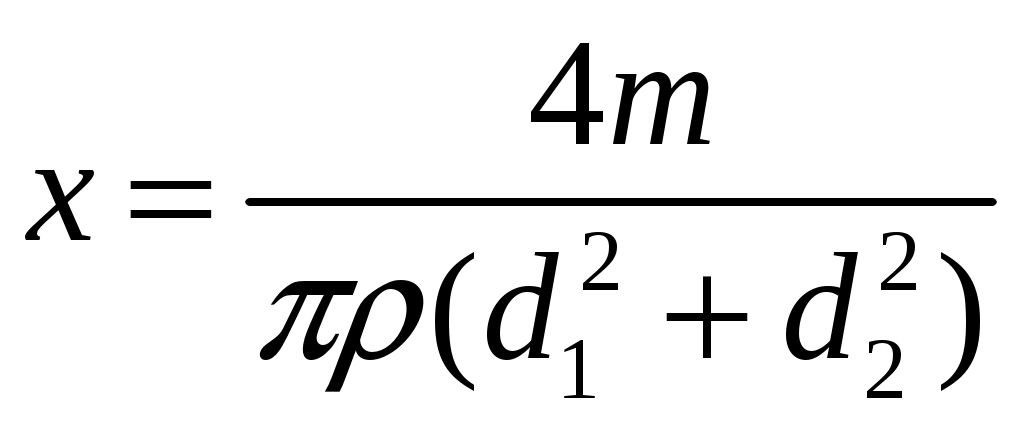

2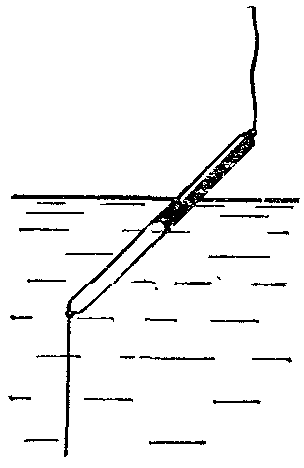


Рис. 20.10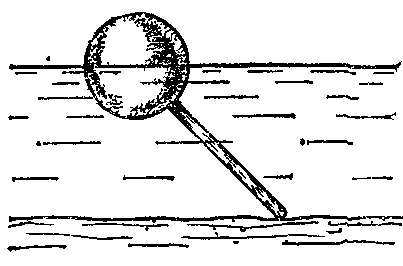




Рис. 20.11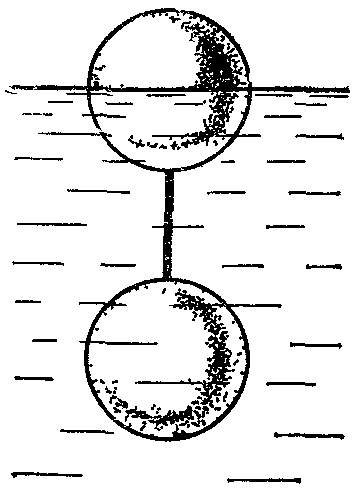




Рис. 20.12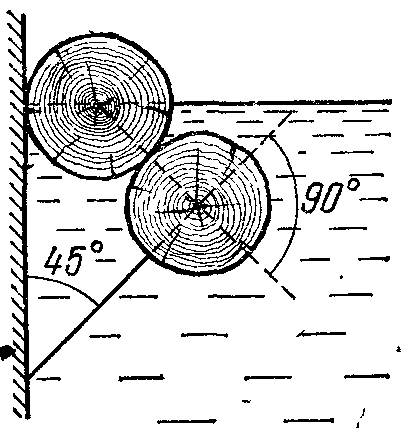



Рис. 20.13

0.10. Определите натяжение нижней лески у поплавка, изображенного на рисунке, если поплавок погружен в воду на ²/₃ своей длины. Масса поплавка 2 г. [F = 9,810^–3 H]

20.11. С какой силой давит тяжелая палочка на дно водоема, если жестко связанный с палочкой пустотелый шарик радиуса rпогрузился в жидкость наполовину? Плотность жидкости , длина палочки l. [ ]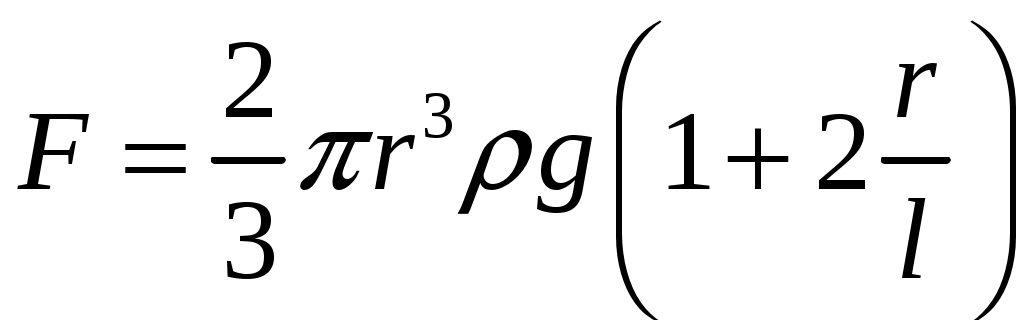

20.12. Определите натяжение нити, связывающей два шарика объема 10 см³, если верхний шарик плавает, наполовину погрузившись в воду. Нижний шарик в три раза тяжелее верхнего. [ H]

20.13. Два одинаковых бревна расположены так, как показано на рисунке. Нижнее бревно привязано к вертикальной стенке тросами, составляющими с ней угол 45°. Верхнее бревно наполовину погружено в воду. Определите плотность бревен. [ = 2/3 г/см³]

20.14. Определите силу давления бревен массы т на стенки канала. Верхнее бревно погружено в воду наполовину, а нижнее касается верхним участком поверхности воды. [ ]

2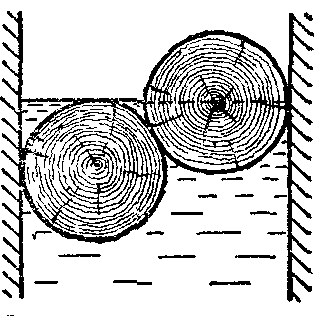


Рис. 20.14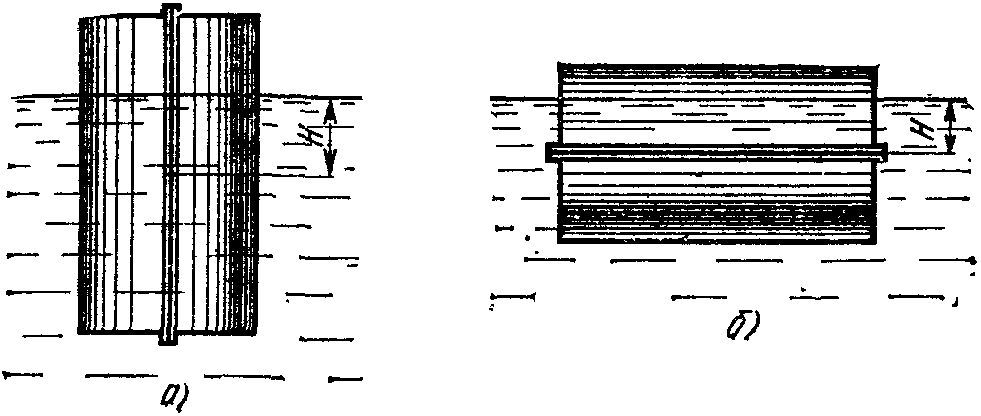




Рис. 20.15

0.15*. Как зависит сила, прижимающая два одинаковых полуцилиндра плавающего батискафа, от глубины его погружения Н,если плоскость соприкосновения полуцилиндров: а) вертикальна; б) горизонтальна? Радиус батискафа R,длина L,плотность жидкости . [a) 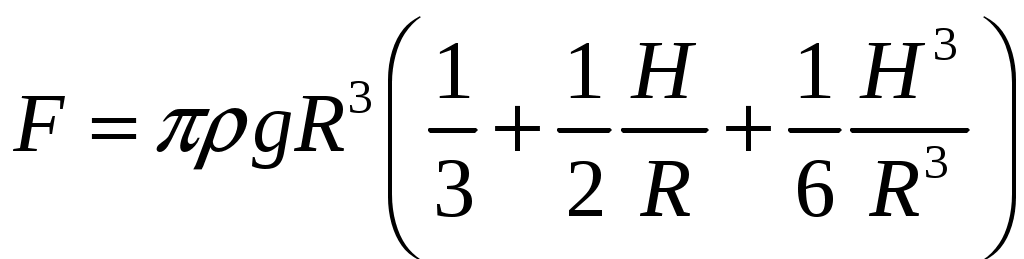, если ; , если H > L/2. б) , если H < R; , если H > R]

20.16*. Докажите, что сила, с которой прижимаются половины сферического батискафа друг к другу, не зависит от наклона плоскости соприкосновения полусфер батискафа, если он полностью погружен в жидкость.

2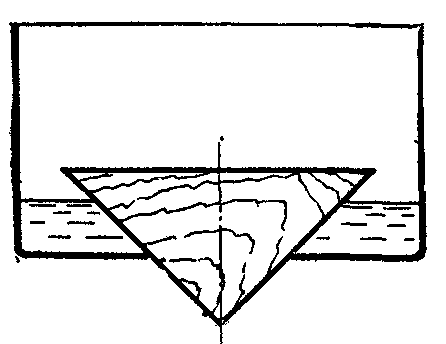


Рис. 2.17
0.17. Коническая пробка высоты 10см с углом при вершине 90° перекрывает отверстие радиуса 5 см. Чему должна быть равна масса этой пробки, чтобы она не всплывала при изменении уровня воды в сосуде? [m = 520 г]

2


Рис. 2.18
0.18*. Решите задачу 20.17 при условии, что отверстие радиуса rперекрывает шар радиуса R, а плотность жидкости равна . [ ]

2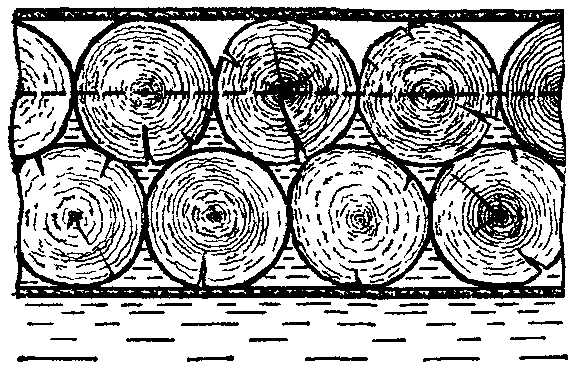


Рис. 20.20
0.19*. Наклон кубической коробки, наполовину погруженной в жидкость, равен а. Определите массу каждого из двух противоположных ребер коробки. Массой остальных частей коробки пренебречь. Плотность жидкости , длина ребер коробки a. [ ; ]

20.20*. Определите минимальное натяжение двух канатов, связывающих широкий плот, состоящий из двух слоев бревен. Масса каждого бревна т. Верхний слой бревен погружен в воду наполовину. [ ]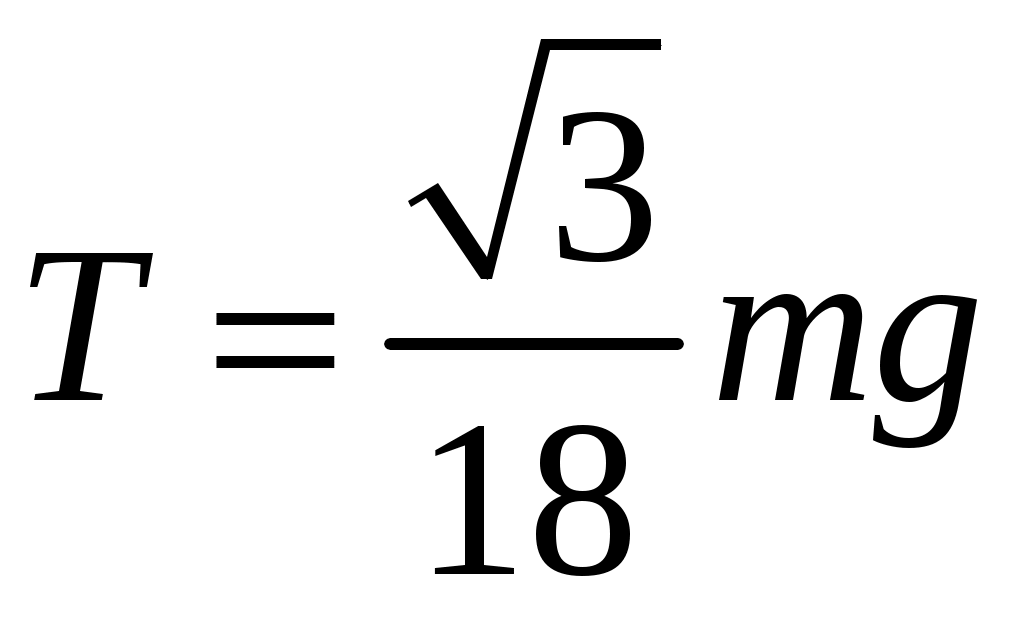

20.21. В цилиндр радиуса R,частично заполненный жидкостью, падает цилиндрическая пробка радиуса rи высоты h. Начальная высота нижнего торца пробки над уровнем жидкости R, начальная скорость равна нулю. Какое количество тепла выделится к моменту окончания движения жидкости и пробки? Плотность пробки , плотность жидкости _o > . [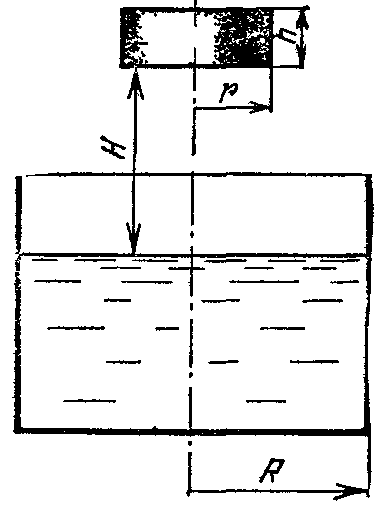


Рис. 20.21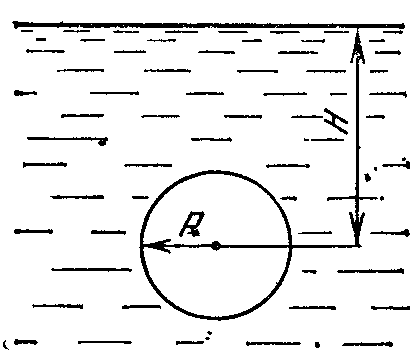




Рис. 20.22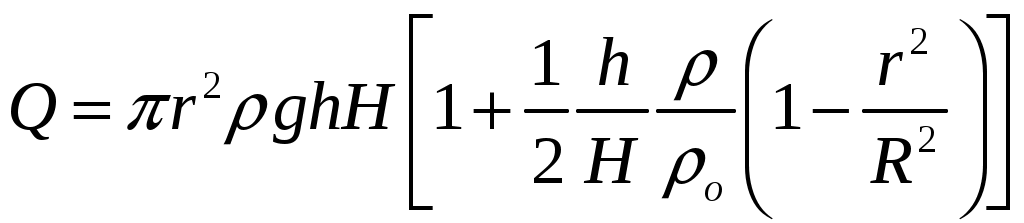

]

20.22. Какое количество тепла выделится в водоеме при всплывании в нем воздушного пузыря радиуса R= 0,1 м с глубины H = 10 м? Плотность воды . [ Дж]

20.23. Какую минимальную работу нужно произвести, чтобы вытащить со дна моря на борт судна батискаф радиуса 2 м? Масса батискафа 35 т, глубина моря 100 м, высота борта судна 3 м. [A = 283 кДж]

20.24*. Для создания искусственной тяжести цилиндрический космический корабль радиуса Rвращается вокруг своей оси с угловой скоростью . Бассейн в корабле имеет глубину H, а дном бассейна служит боковая стенка корабля.

а) Сможет ли космонавт плавать в этом бассейне? Опишите особенность космического бассейна. Определите плотность плавающей в бассейне палочки длины l < H, если из воды выступает ее верхняя часть длины . [a) Сможет. ]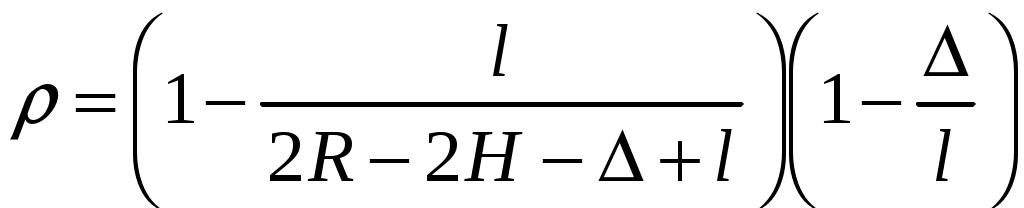

б) В бассейне можно наблюдать следующее интересное явление: два шара разной плотности, связанные нитью, в зависимости от «глубины» движутся или к свободной поверхности, или к стенке космического корабля, если плотность одного шара больше, а другого меньше плотности воды. Объясните это явление.

2


Рис. 20.26
0.25. Цилиндрический сосуд радиуса R,заполненный жидкостью плотности _o, вращается с угловой скоростью со вокруг своей оси. В сосуде находится шарик радиуса rи плотности  > _o. Найдите силу, с которой шарик давит на боковую стенку сосуда. [ ]

20.26. Цилиндрический сосуд радиуса R,частично заполненный жидкостью, вращается вместе с жидкостью вокруг своей оси. К боковой стенке сосуда на нити длины l привязан воздушный шарик радиуса r;во время вращения нить образует со стенкой угол . Определите угловую скорость вращения. Поле тяжести направлено вдоль оси сосуда. [ 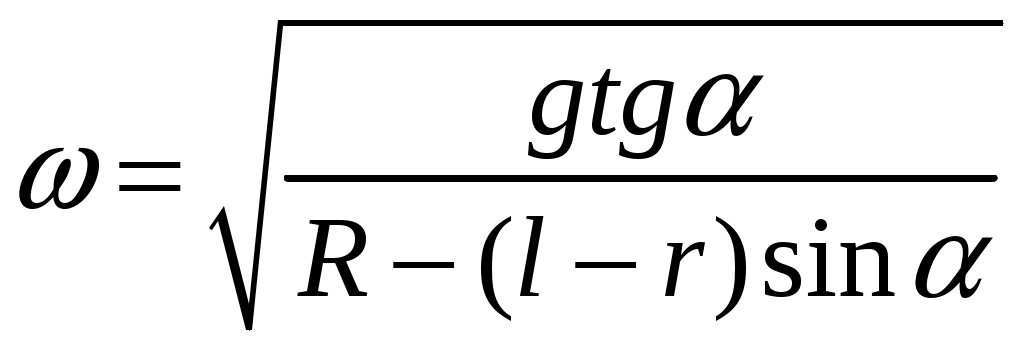]