Статика - ИТОГ. Сборник задач по физике. Грабцевич В. И. Сборник задач по физике
 Скачать 1.12 Mb.
|
|
2 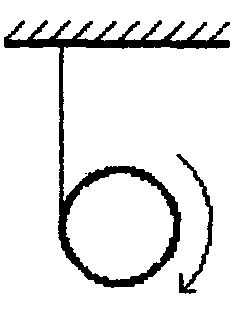 Рис. 5 3.18. На однородный диск массой m намотана нить. Свободный конец нити привязали к потолку и диск отпустили. Определить силу натяжения нити в процессе опускания диска. Считать, что нить все время вертикальна (рис. 23.5). 23.19. Однородный стержень массой m подвешен горизонтально за концы на двух вертикальных нитях. Одна из нитей обрывается. Какова сила натяжения второй нити в момент обрыва? 2 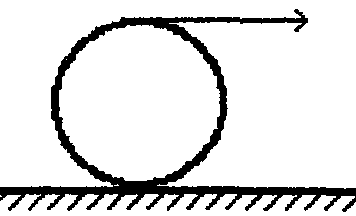 Рис. 6 3.20. Неподвижный блок представляет собой однородный цилиндр массой m. Через блок перекинута невесомая нить, к концам которой привязаны грузы массами m1 и m2. Определить ускорение грузов и силу натяжения нити слева и справа от блока при свободном движении системы. Проскальзывания нити и трения в блоке нет. 2 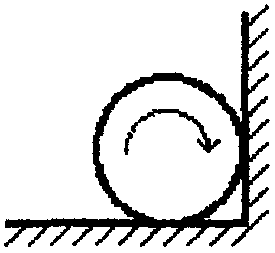 Рис. 7 3.21. На однородный цилиндр массой m и радиусом R, лежащий на горизонтальной поверхности, намотана тонкая нить. За нить тянут горизонтальной силой F (рис. 23.6). При каком значении коэффициента трения цилиндр не будет проскальзывать по поверхности? 23.22. Однородный цилиндр лежит на горизонтальной поверхности. Второй такой же цилиндр катится на первый со скоростью v. Оси цилиндров параллельны. Между цилиндрами происходит абсолютно упругий удар. Определить конечные установившиеся скорости движения цилиндров. 23.23. Тонкостенную трубу радиусом R раскрутили вокруг оси до угловой скорости и положили в угол между полом и стеной параллельно ребру угла (рис. 23.7). Коэффициент трения между трубой и стеной равен , а между трубой и полом – 2. Сколько оборотов сделает труба до остановки? 23.24. Горизонтально расположенный деревянный стержень массой М и длиной l может вращаться вокруг вертикальной оси, проходящей через его середину. В конец стержня попадает и застревает в нем пуля массой m, летящая со скоростью v перпендикулярно стержню и оси его вращения. С какой угловой скоростью начнет вращаться стержень? 23.25. По гладкой горизонтальной поверхности по окружности движется небольшое тело, привязанное к нити. Нить продета в маленькое отверстие в поверхности. Нить начинают медленно втягивать в отверстие, уменьшая радиус окружности движения тела. Как зависит сила натяжения нити от радиуса окружности? Масса тела равна m. Считать, что при радиусе равном Ro угловая скорость движения тела была равна о. 23.26. На массивный неподвижный блок в виде цилиндра радиусом R намотана нить, к свободному концу которой подвешен груз массой m (рис. 23.4). В момент t = 0 систему отпускают. Написать зависимость момента импульса системы относительно оси блока от времени. Трения нет. 2 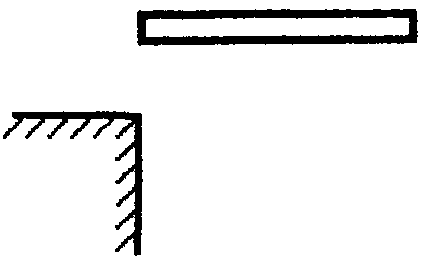 Рис. 8 3.27. Стержень, расположенный горизонтально, падает без начальной скорости с высоты h и ударяется одним концом о край стола (рис. 12.8). Определить скорость центра масс стержня сразу после удара. Удар абсолютно упругий. 2 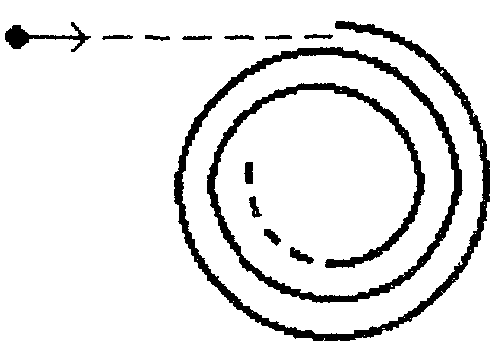 Рис. 9 3.28. Шарик массой m влетает в спиральный лабиринт, который может свободно двигаться в пространстве, и останавливается в его центре (рис. 23.9). Начальная скорость шарика равна v, радиус лабиринта R, масса лабиринта М, его момент инерции J. Определить угловую скорость вращения лабиринта после того как шарик остановится. Размерами шарика и внешними силами пренебречь. 23.29. Два диска, имеющие моменты инерции J1 и J2, вращаются на одной оси с угловыми скоростями 1 и 2 Диски прижимают друг к другу. Определить установившуюся угловую скорость вращения и количество теплоты, выделившееся при трении дисков. 23.30. Тонкий стержень длиной l и массой M стоит вертикально на гладкой горизонтальной поверхности. В его верхний конец попадает горизонтально летящая пуля массой m (m << М) и застревает в нем. При какой минимальной скорости пули стержень сразу оторвется от поверхности? Ответы [Механика твердого тела. Момент импульса]: 23.1. Увеличится 23.2. 0,5 23.3.  23.4.  23.5. 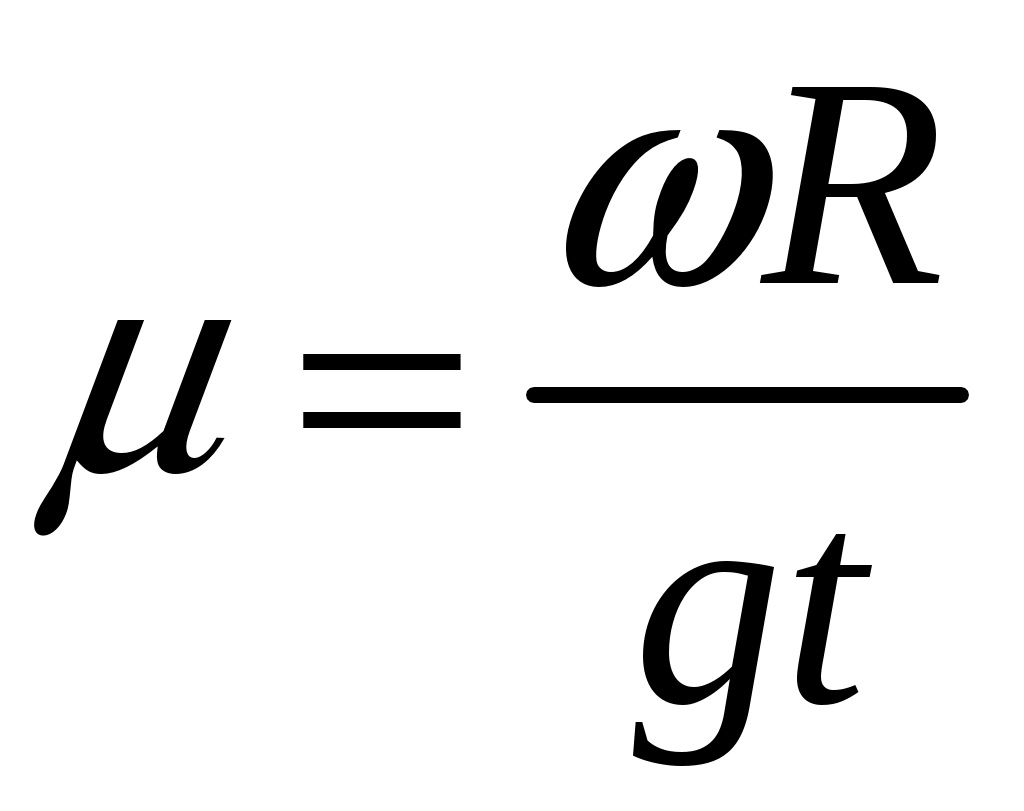 23.6. 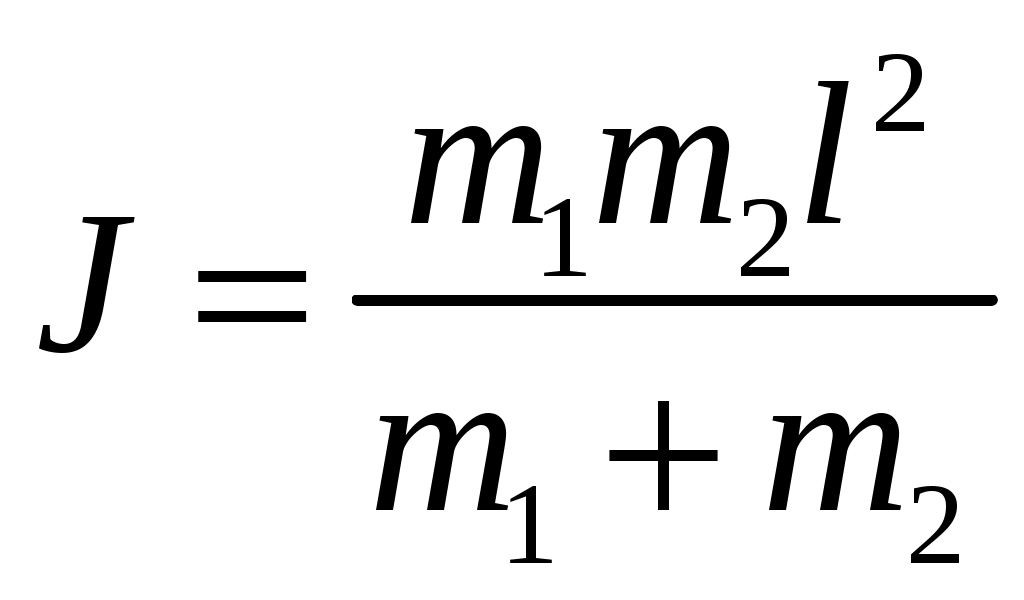 23.7.  23.8. 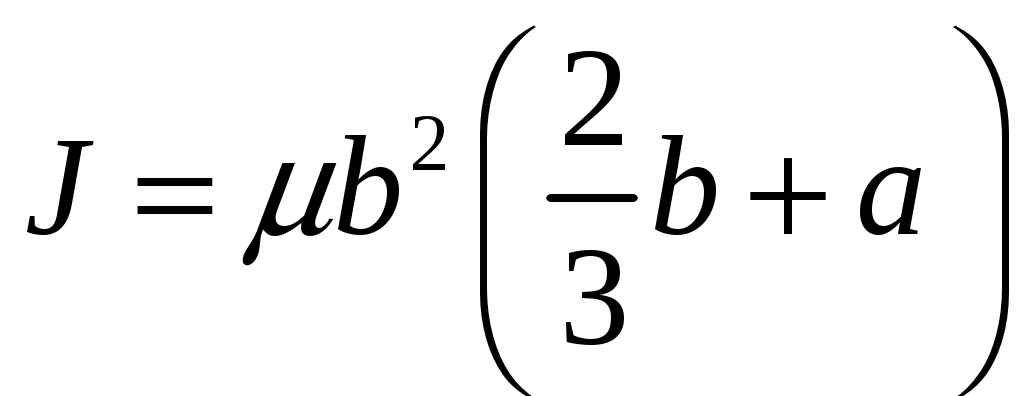 23.9. 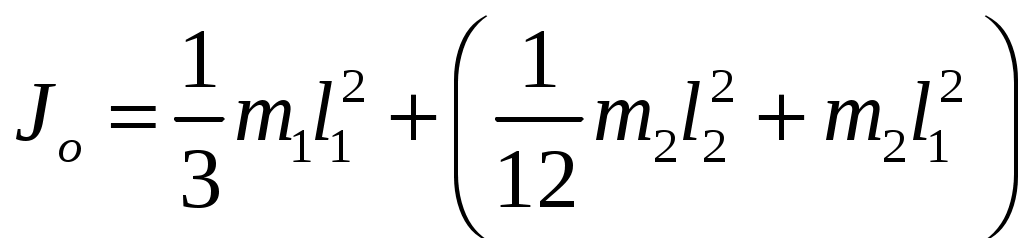 23.10. 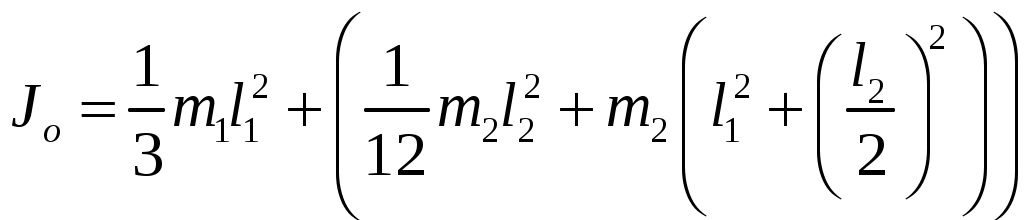 23.11.  . Указание: Если в 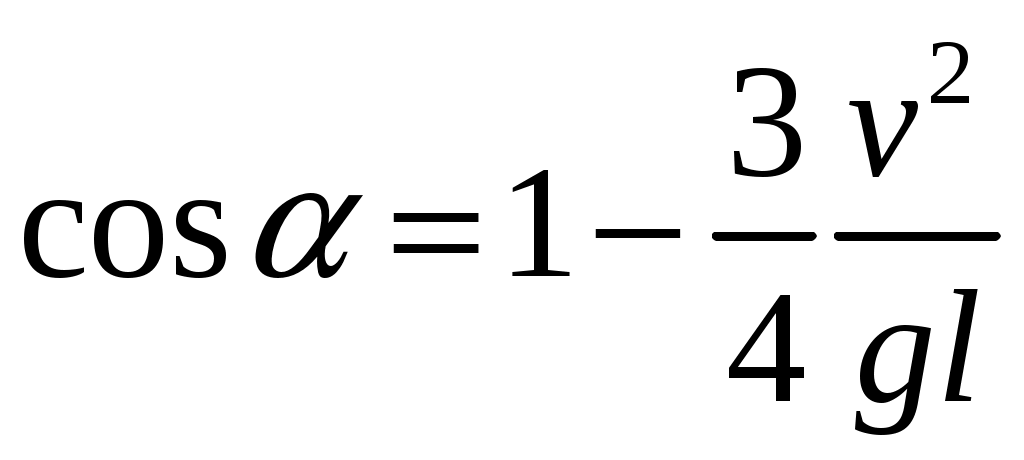отверстие вставить вырезанный из него диск, то получится сплошной диск, момент инерции которого складывается из момента инерции большого диска с отверстием и момента инерции маленького диска относительно центра большого диска.23.12. а)  ; б)  ; в)  23.13.  23.14.  23.15.  23.16. 100 см 23.17.  23.18.  23.19.  23.20. 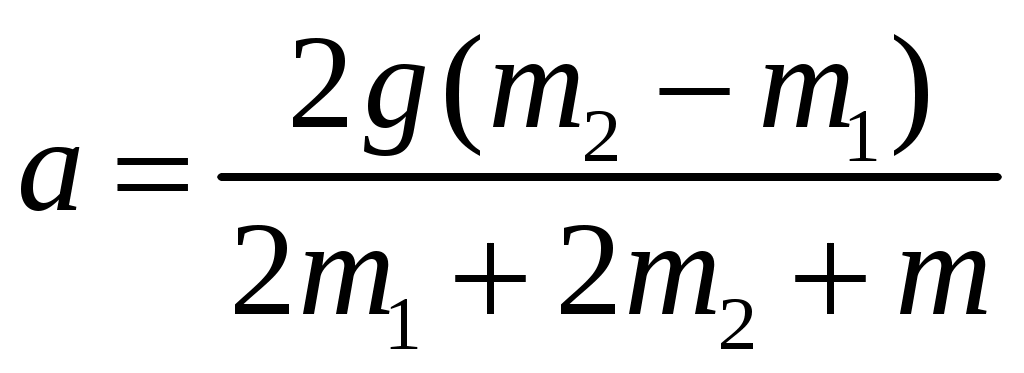 ;  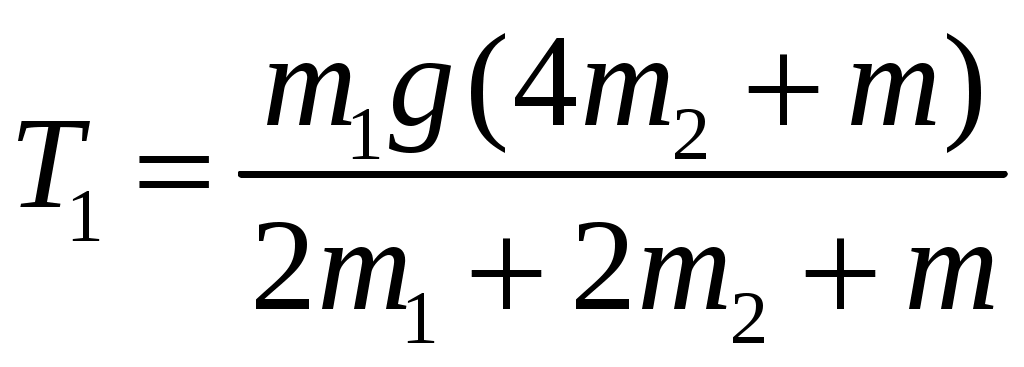;  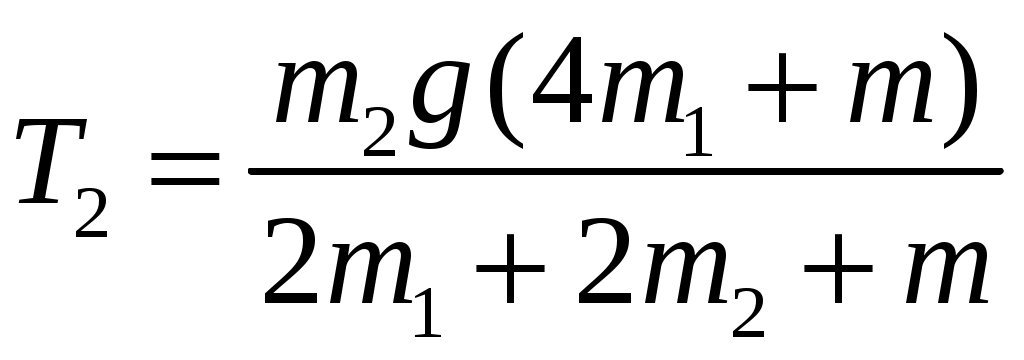23.21. 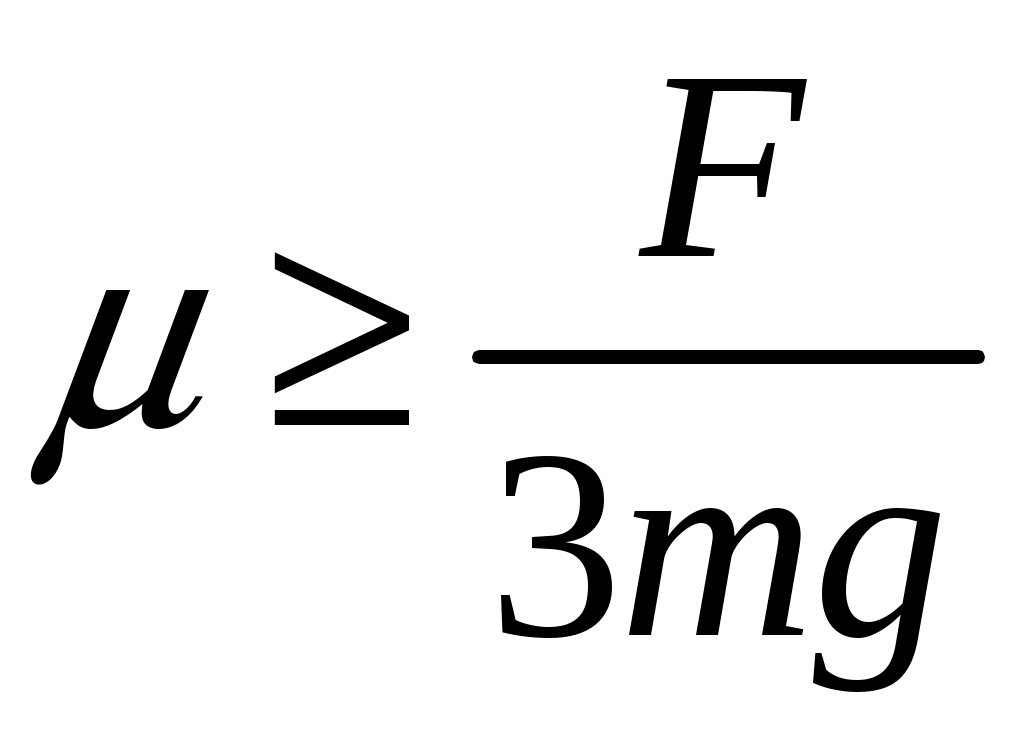 23.22.  . Указ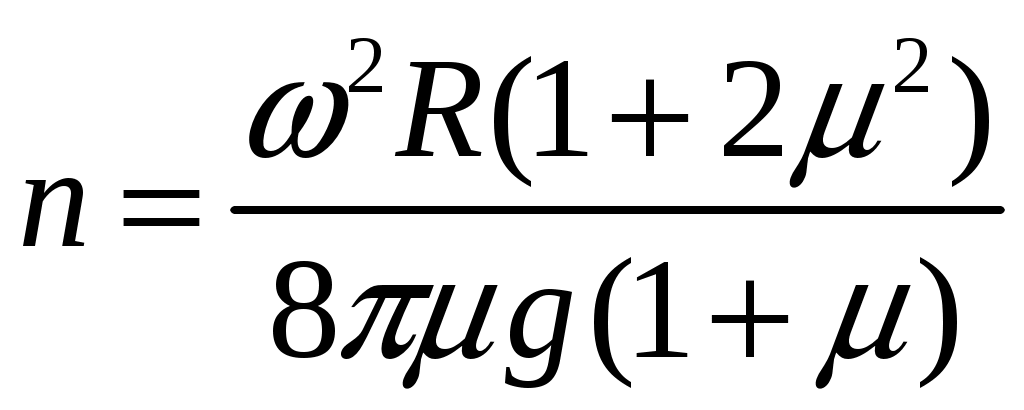ание: после столкновения первый цилиндр остановится, продолжая вращаться с угловой скоростью  , а второй – приобретет поступательную скорость v при отсутствии вращения. За счет проскальзывания первый цилиндр будет разгоняться, а второй замедляться. Скорости цилиндров установятся, когда прекратится проскальзывание.23.23.  23.24. 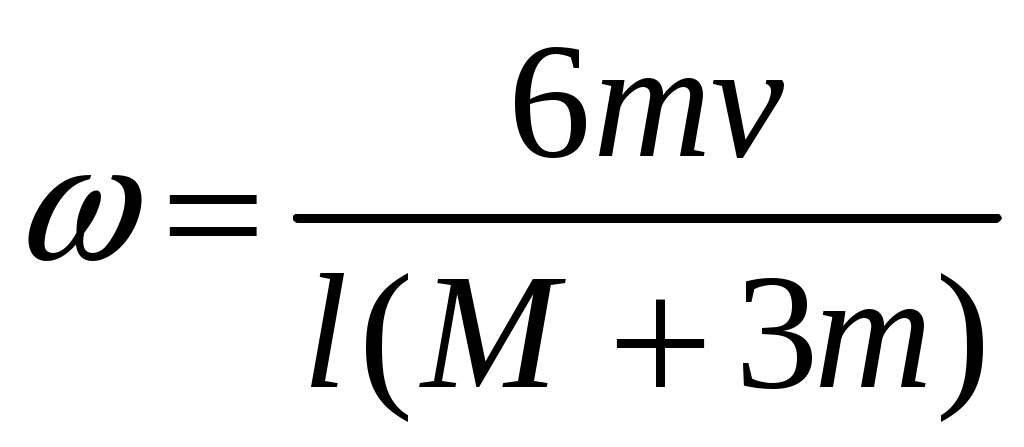 23.25.  23.26.  23.27. 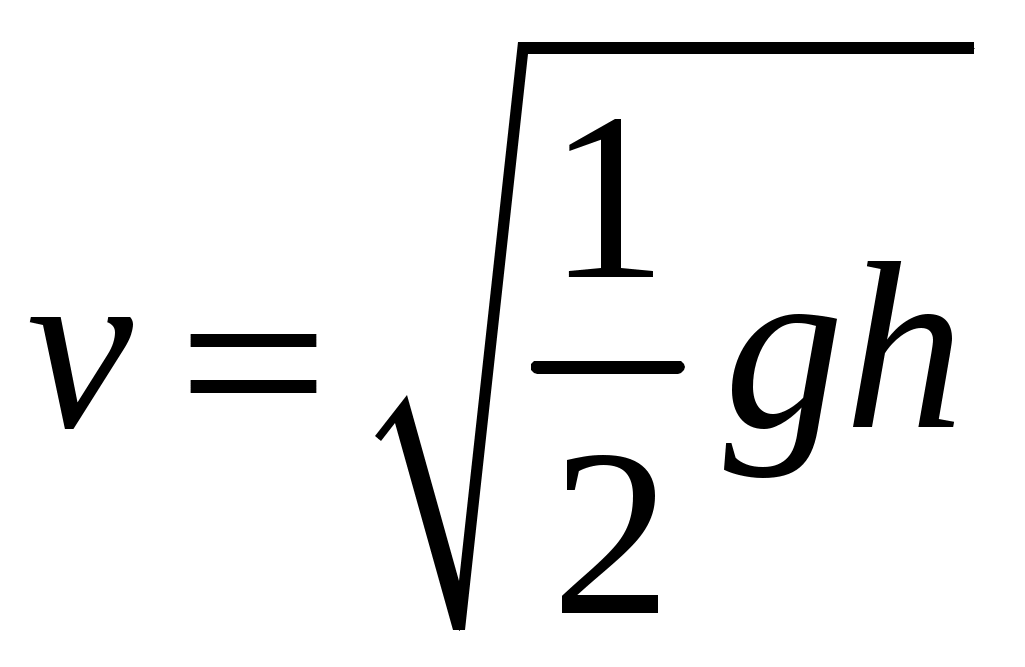 . Указание: Так как удар упругий, то кинетическая энергия стержня перед ударом  равна его кинетической энергии после удара, которая равна сумме энергии движения центра масс стержня  и энергии его вращения вокруг центра масс  . В результате удара о стол стержень приобретает момент импульса  ,  – импульс силы удара; l – длина стержня. Кроме того, изменение импульса стержня  равно импульсу силы удара.23.28.  . 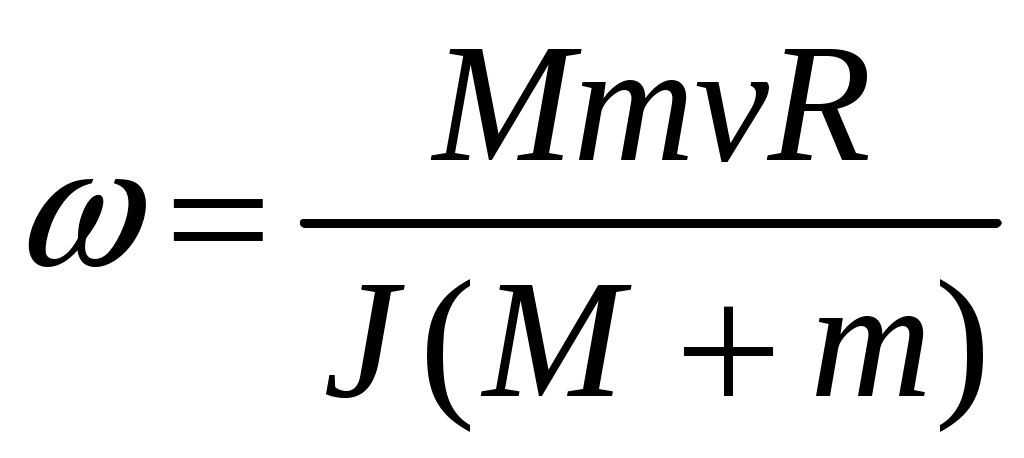Указание: Центр масс системы будет все время двигаться равномерно со скоростью  вдоль линии центра масс, которая проходит на расстоянии  от центра лабиринта. После остановки шарика центр лабиринта переместится на линию центра масс. Закон сохранения момента импульса следует записать относительно этой линии.23.29.  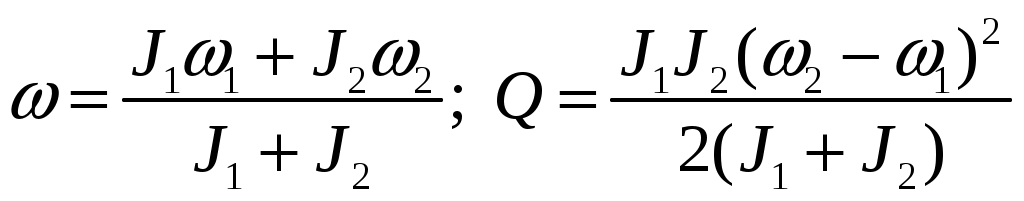.23.30. 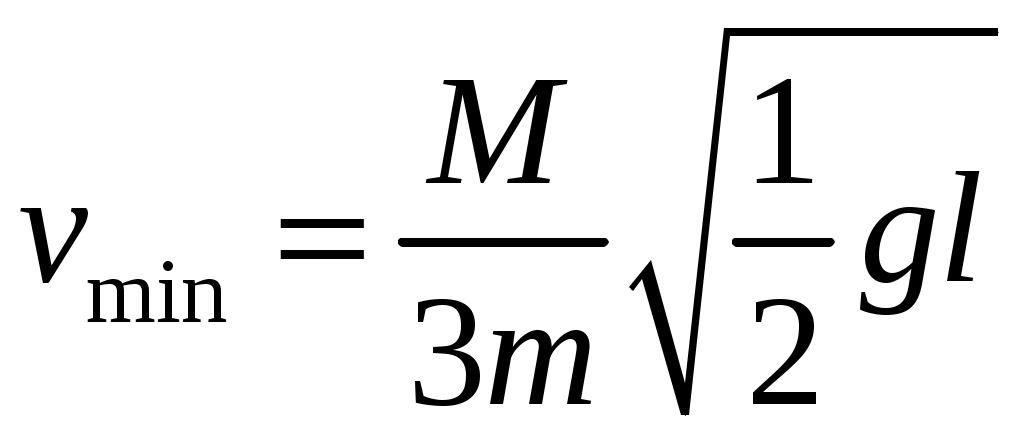 . Указание: Движение стержня сразу после удара можно, представить как движение центра масс стержня (m << M) со скоростью и вращение вокруг центра масс. Стержень сразу оторвется от поверхности, если в системе центра масс центростремительное ускорение его нижнего конца будет больше, чем g. Закон сохранения момента импульса:  . |