Сборник СОР и СОЧ 7 класс рус. Сборник заданий для
 Скачать 0.83 Mb.
|
3 вариантДаны отрезок СД, точка А, не лежащая на прямой СД, и точка В, лежащая на прямой СД. Каково взаимное расположение прямой АВ и отрезка СД? Рассмотрите два случая. [2 балла] Найдите углы, образованные при пересечении двух прямых, если один из них равен равен 54о [2 балла] Точки M, Nи Kрасположены на одной прямой, причем MN=15см, NK=3см. Какой может быть длина отрезка MK? Рассмотрите два случая. [2 балла] 7. Дан угол АОВи точка С, не лежащая в его внутренней области. а) Постройте луч CD, который пересекал бы лучи ОАи ОВ. Постройте развернутый угол СОК. Какие из точек А, В, С лежат во внутренней области тупого угла КОА?  В[3 балла] На рисунке прямые aи bперпендикулярны, 1 = 1500 . 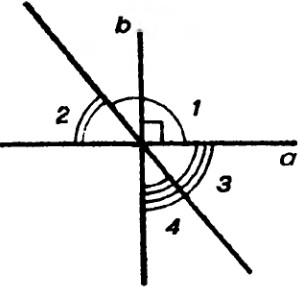 Найдите углы 2, 3 и 4[3 балла] На прямой отложены два равных отрезка ДСи СЕ. На отрезке СЕвзята точка М, которая делит его в отношении 2:7, считая от точки С. Найдите расстояние между серединами отрезков ДСи МЕ, если CМ=6 см. [3 балла] От стороны развернутого угла АОВ в одну полуплоскость отложены АОК = 40о и АОЕ = 60о. Найдите угол между биссектрисами углов КОЕи ЕОВ. [5 баллов] Задания суммативного оценивания за 2 четверть 1 вариант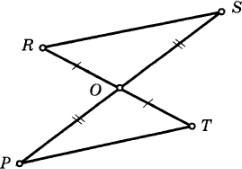 На рисунке RO=OT, SO=OP. Докажите, что ΔROS= ΔTOP.[2 балла] Две стороны равнобедренного треугольника 9 см и 6 см. Каким может быть периметр этого треугольника? [2 балла] На рисунке В = С, ВО = СО. Докажите, что треугольник АОD – равнобедренный. 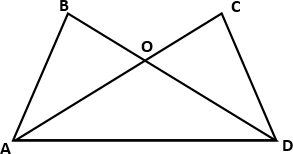 [3 балла]На рисунке СD=DЕ, СР=РЕ, FСР= КEР. Докажите, что DF=DK. 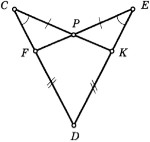 [4 балла]В треугольнике АВСточка М– середина стороны АС, ВМА= 90º , АВС= 40º , ВАМ= 70º. Найдите углы МВСи ВСА. [4 балла] В треугольнике АВС известно, что АВ=ВС=18 см. Серединный перпендикуляр к стороне АВпересекает сторону ВСв точке Е. Найдите основание АС, если периметр треугольника АЕСравен 27 см. 5 баллов] |