вся навигация 2. Счисление пути судна

• Название: Счисление пути судна
• Дата: 31.01.2023
• Размер: 2.02 Mb.
• Имя файла: вся навигация 2.doc
• Тип: Решение; #914065
• страница: 3 из 7

Способ С.И. Дёмина. Для вычисления угла дрейфа С.И. Дёмин предложил формулу

, (4.25)

где с, b - коэффициенты; Т - осадка судна, м; q - курсовой угол, град; V - скорость судна, уз; W -скорость кажущегося ветра, уз.

Коэффициенты с и b различны для каждого судна и зависят от отношения площади надводной части судна к площади подводной части S_н / S_п для различных осадок судов Т. Эти коэффициенты вычисляются заранее. Для их вычисления, задаваясь осадкой с интервалом в 1 м, из чертежа выбирают значения L - длины судна, В - ширины, S_н / S_п - отношения площадей и  - коэффициент продольной полноты. По выбранным данным для различных значений Т_i вычисляют

(4.26)

По отношениям S_н / S_п вычисляют .

Значения К_i получаются в функции Т и обычно имеют вид

К_i = се^-bT. (4.27)

Построив график, выбирают два значения К, например, для осадок Т₁ = 5м и Т₂ = 10м. Прологарифмировав выражения (4.27), получают два уравнения

l 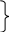nК₁ = lnс - bТ₁

(4.28)

lnК₂ = lnc - bT₂

Решив эти уравнения получают значения коэффициентов с и b. Измерив W и q и, зная с и b, можно вычислить угол дрейфа  по формуле (4.25) для данной осадки. Для облегчения вычислений могут быть составлены таблицы или номограммы.

Учёт дрейфа при прокладке.

Все относительные лаги учитывают только составляющую скорости судна относительно воды, направленную по диаметральной плоскости судна, а при наличии дрейфа на линии ПУ_ надо откладывать расстояния, фактически проходимое судном по линии пути, т.е.

S = S_л sec  = РОЛ К_л sec . (4.29)

В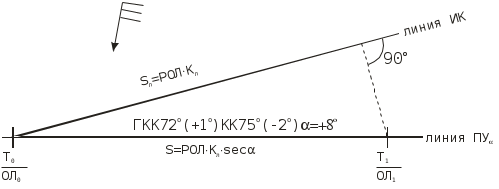


Рис. 4.19. Прокладка с учетом угла дрейфа более 6
еличину S можно получить графически или рассчитать по формуле (4.29). При графическом учёте S на карте от исходной точки учёта дрейфа прокладываются две линии: линия ИК и линия ПУ_ (рис.4.19). Расстояние, пройденное по лагу (S_л = РОЛ  К_л), откладывается по линии ИК и переносится перпендикулярно линии ИК на линию пути. Над линией ПУ_ делаются записи ГКК и в скобках ГК, КК и в скобках МК и затем значение угла  с его знаком. Таким образом надпись показывает курс, который держит рулевой (ГКК), истинный курс (ГКК + ГК и КК + МК) и направление линии пути, которым следует судно (алгебраическая сумма ИК и ). Если S учитывается аналитически, то от исходной точки начала учёта дрейфа прокладывается отрезок линии ИК длиной 3 – 4 см и линия ПУ_ = ИК + ( ), на которой непосредственно откладывается, рассчитанная по формуле (4.29) величина S.

Учёт S, полученного по формуле (4.29), производится при   6.

Е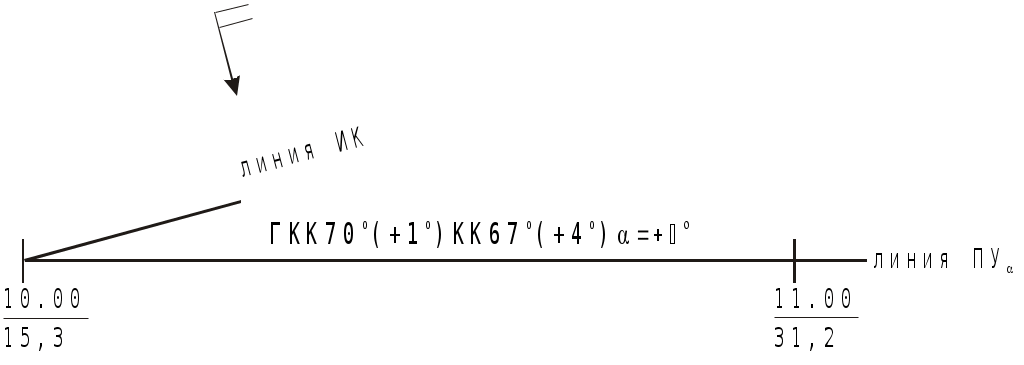
Рис. 4.20. Прокладка с учетом угла дрейфа менее 6
сли   6, то погрешность от неучёта sec  меньше 0,5% поправки лага и в этом случае можно откладывать пройденное расстояние по лагу S_л = РОЛ  К_л непосредственно на линии ПУ_, а линию ИК показывать отрезком (рис.4.20), как при аналитическом учёте S.

Если лаг не работает и скорость судна определяется по оборотам, необходимо использовать таблицы и графики, характеризующие потерю скорости в зависимости от силы и курсового угла ветра. Такие таблицы должны быть на каждом судне.

Счислимые точки наносятся на линии пути. При учёте дрейфа также решают две задачи: прямую и обратную. При прямой задаче, зная ИК, рассчитывают ПУ_ и прокладывают линию ПУ_ на карте: ПУ_ = ИК +  = ГКК + ГК + . При обратной задаче рассчитывают ГКК, который надо задать рулевому: ГКК = ПУ_  ГК.

Д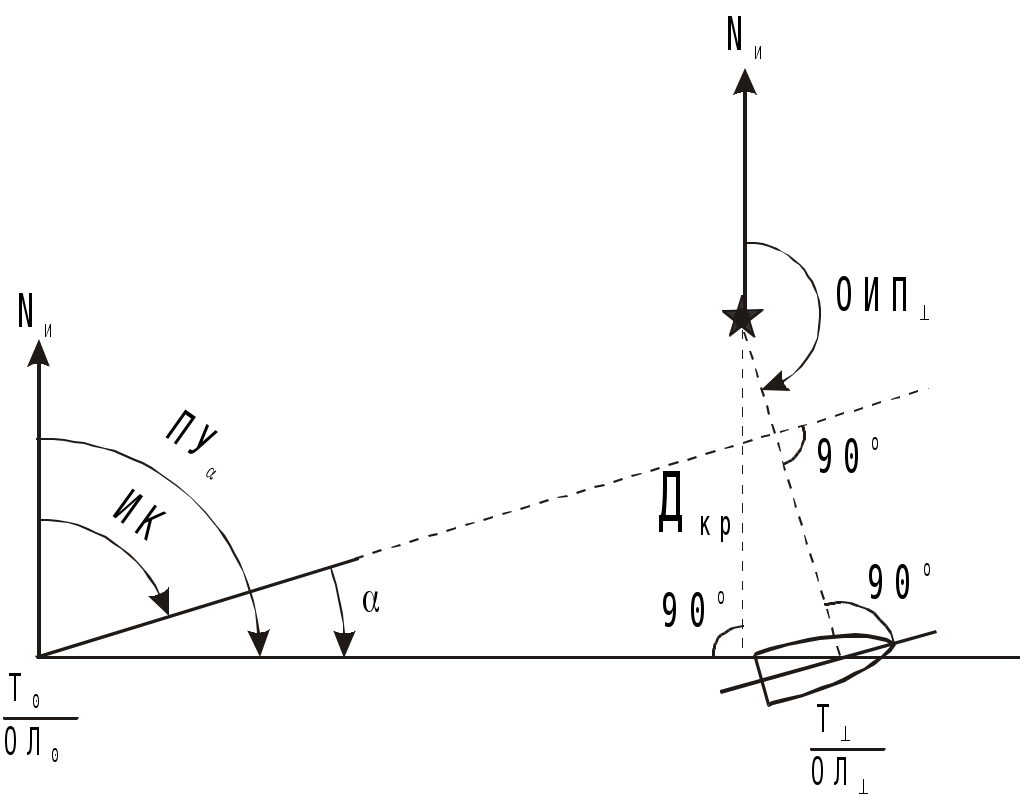
Рис. 4.21. Траверз и кратчайшее расстояние при учете дрейфа
ля нахождения счислимого места судна на момент когда какой-либо ориентир будет на траверзе или любом другом курсовом угле, надо рассчитать истинный пеленг этого ориентира и линию пеленга (ОИП = ИК+ КУ  180) провести от ориентира до пересечения с ПУ_ (рис.4.21). Время и отсчёт лага в момент прихода на траверз или на заданный КУ рассчитывается, как в 4.1.1, снимая S при   6 или S_л при   6 по линии ПУ_.

Учёт дрейфа при использовании автоматического счислителя координат сводится к введению дополнительной поправки курса, равной углу дрейфа. Для этого на приборе устанавливается поправка курса К_, равная алгебраической сумме поправки компаса и угла дрейфа

К_ =  ГК + . (4.30)

При каждом изменении курса или скорости судна, скорости и направлении ветра поправка курса должна вычисляться и устанавливаться заново.

Определение и учёт дрейфа с застопоренными машинами.

Судно в этом случае перемещается по направлению ветра со скоростью

V_др =K_v W, (4.31)

гле К_v - коэффициент дрейфа без хода, W - скорость наблюденного ветра, уз.

Для определения скорости дрейфа рекомендуется произвести испытания. При различных скоростях W с помощью РЛС по измеренным расстояниям до объекта S_др = D₂  D₁ в милях и замеченному промежутку времени t в секундах рассчитать скорость в узлах:

. (4.32)

S_др может быть также получено, если расстояния D₁ и D₂ измерены секстаном по углу снижения.

При наличии 30 - 40 наблюдений коэффициент дрейфа без хода вычисляется по формуле

, (4.33)

где V_дрW = V_др1W₁ + V_др2W₂ + .... + V_дрnW_n; WW = W²₁ + W²₂ + .... + W²_n.

Зная К_v вычисляют V_др, а затем и расстояние S_др = V_дрt, которое откладывают от исходной точки по направлению ветра.

Судоводитель обязан использовать приведённые методы для регулярного определения угла дрейфа и коэффициента дрейфа без хода, чтобы накопить опытные данные о дрейфе своего судна при различных условиях плавания.

Если К_v находится в пределах 0,056-0,062, то измерив скорость ветра, можно скорость ветрового дрейфа без хода, вместо расчета по формуле (4.31) выбрать из таблицы 2.22 МТ – 2000.

Морские течения и учёт постоянного течения при прокладке.

Горизонтальные перемещения водных масс в морях и океанах под влиянием различных факторов называются морскими течениями.

Элементами течения являются его скорость _т и направление К_т. Направление течения имеет название той точки горизонта, куда оно движется (“ветер дует в компас, а течение идёт из компаса”). Направление течения обычно выражается в градусах, а иногда в румбах. Например течение 45 означает, что оно направлено на NE. К_т - это направление течения относительно N_и. При аналитическом расчёте течения используются направления течения относительно линии курса - q_т и относительно линии пути - Р_т. Скорость течения _т указывается в узлах, а в некоторых навигационных пособиях в десятых долях узла.

В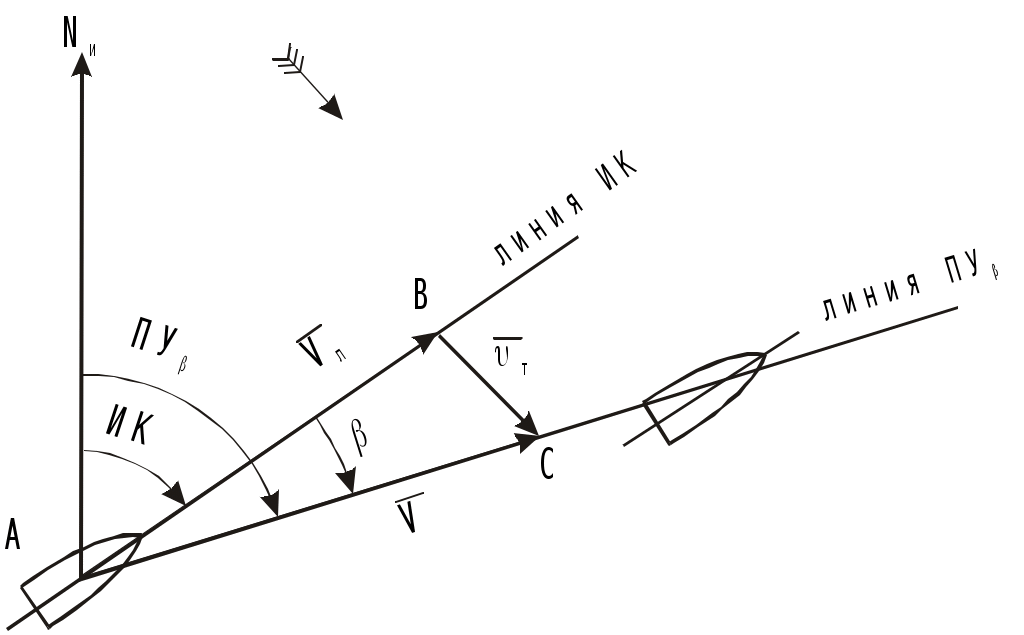
Рис. 4.22. Построение навигационного треугольника при прямой задаче учета течения
зависимости от устойчивости морские течения подразделяются на: постоянные - скорость и направление которых из года в год остаются постоянными (например течения, вызываемые пассатами); учёт их прост и сведения о них достаточно достоверны; периодические - скорость и направление которых периодически меняются (например течения, вызываемые муссонами и приливо-отливные течения); т.к. скорость и направление этих течений зависят от многих факторов (астрономических данных, конфигурации берега, рельефа дна и др.), то сведения о таких течениях могут содержать значительные ошибки; временные - скорость и направление этих течений зависят от величины и продолжительности действия образующих течения временных сил (ветра, изменения плотности воды, изменения атмосферного давления и др. причины); сведения о них ориентировочные и учёт их приближённый.

Под действием судового двигателя судно получает движение относительно воды по направлению ДП, которое определяется ИК. При наличии течения вода сама имеет движение относительно Земли, следовательно скорость судна относительно Земли определится геометрической суммой

V = V_л + _т (4.34)

и судно будет перемещаться по направлению вектора V (рис.4.22).

Треугольник АВС, сторонами которого являются векторы трёх скоростей, называется навигационным треугольником или треугольником скоростей, который необходимо строить при учёте течения. Линия АС, по которой перемещается судно при течении, называется линией пути при течении, а угол между северной частью истинного меридиана и линией пути при течении называется путевым углом при течении ПУ_.

Угол  между линией пути при течении и линией курса называется углом сноса от течения и рассчитывается по формуле

 = ПУ_  ИК. (4.35)

Связь между ИК, ПУ_ и  определяется алгебраическими формулами

ПУ_ = ИК + (   ) и (4.36)

ИК = ПУ_  (   ). (4.37)

Знак  зависит от направления сноса. Если течение направлено в левый борт, то  будет иметь знак “+”, при течении в правый борт - знак “”.

Так как рулевой удерживает судно на истинном курсе, то судно, перемещаясь по линии пути со скоростью V, называемой путевой (истинной) скоростью (скоростью относительно дна), имеет ДП параллельную ИК (см. рис.4.22).

При плавании на течении, также как и при учёте дрейфа, решаются две задачи: прямая и обратная.

П
Рис. 4.23. Обратная задача при учете течения
рямая задача. По заданным ИК,V_л, К_т и необходимо найти ПУ_,  и V. Для получения пути строят навигационный треугольник: из исходной точки начала учёта течения прокладывают ИК, на котором в условном масштабе откладывают вектор скорости судна V_л. Из конца этого вектора проводят вектор скорости течения в том же масштабе. Соединив начальную точку с концом вектора , получают линию пути судна и путевую скорость V. Угол , ПУ_ и V снимаются непосредственно с карты (рис.4.22).

Обратная задача. По заданным ПУ,V_л, К_т и необходимо найти ИК, а в конечном итоге ГКК, который должен держать рулевой, чтобы судно шло по намеченному на карте пути, угол  и V. Для получения истинного курса также надо построить навигационный треугольник. Его построение производится следующим образом: на карте проложена линия пути. Из исходной точки в условном масштабе проводят вектор скорости течения , из конца которого в том же масштабе радиусом равным скорости судна по лагу V_л делают засечку на линии пути; отрезок от исходной точки до полученной точки на линии пути и есть путевая скорость V (в том же масштабе). Далее соединяют тонкой прямой начальную точку с полученной точкой и эту линию переносят параллельно в исходную точку. Полученная линия и есть линия истинного курса, направление которой снимается с карты (рис.4.23). Угол между линией пути и линией курса в этом случае называется поправкой на снос от течения.

По снятому с карты ИК рассчитывают ГКК = ИК  ГК, который дают рулевому.

Особенности графических построений на карте при учёте течения.

1. 
   На карте прокладываются и линия курса (ИК) и линия пути (ПУ).
   
2. 
   При построении навигационного треугольника вектора скорости судна и течения берутся в одном условном масштабе. Обычно берется количество миль в масштабе карты, проходимое за час или на крупномасштабных картах за полчаса. Этот треугольник является частью навигационной прокладки и не стирается до конца рейса.
   
3. 
   Путевая (истинная) скорость - это вектор навигационного треугольника по линии пути.
   
4. 
   При изменении хотя бы одного из четырёх элементов: курса судна, скорости судна, направления или скорости течения необходимо построить новый навигационный треугольник.
   
5. 
   Для получения счислимой точки пройденное по лагу расстояние S_л (исправленная разность отсчётов лага) откладывается по линии курса и переносится по направлению течения на линию пути (рис.4.23).
   
6. 
   Для расчёта отсчёта лага и времени прохода судном заданной точки С (см. рис.4.23) на линии пути, проводится линия из этой точки по направлению обратному направлению течения до пересечения её с линией курса (точка В на рис.4.23). С карты снимается расстояние АВ, которое судно должно пройти относительно воды и рассчитывается ОЛ_в =ОЛ_а + S_л / К_л и время Т_в=Т_а +S_л/V_л.
   
7. 
   Время и отсчёт лага прихода ориентира на траверз судна или, в общем случае, на заданный КУ определяется так: рассчитывается траверзный ИП_= ИК  90 (в общем случае ИП = ИК  КУ ) и от ориентира проводится ОИП_ (в общем случае ОИП) до пересечения с линией пути - точка F (рис.4.23) (судно одновременно будет находиться на линии пути и на линии пеленга). Далее действия те же, как и для расчёта ОЛ и Т прихода судна в заданную точку (см. п.6).
   
8. 
   Вместо прокладки на карте двух линий: линии курса и линии пути, часто прокладывают одну линию пути ПУ_ и находят на ней точки, откладывая пройденные расстояния по линии пути, рассчитанные по формуле S =V  t, где V - путевая, (истинная) скорость, которая снята с навигационного треугольника, построенного на свободном месте карты в стороне от истинного местонахождения судна. Такой способ учёта течения при прокладке удобен при отсутствии лага, когда скорость судна относительно воды определяется по оборотам. Этот способ можно применять и при наличии лага, откладывая по линии ПУ_ расстояние, пройденное по линии пути S = S_лК, где К = V / V_л.
   
9. 
   При учёте попутного и встречного течения ПУ_ = ИК и  =0. Рассчитывается снос судна течением за время плавания
   

S_т = _т (Т₂ Т₁), (4.38)

и тогда фактически пройденное расстояние S будет равно

S = S_л  S_т , (4.39)

при попутном течении будет знак “+”, при встречном знак “”.

С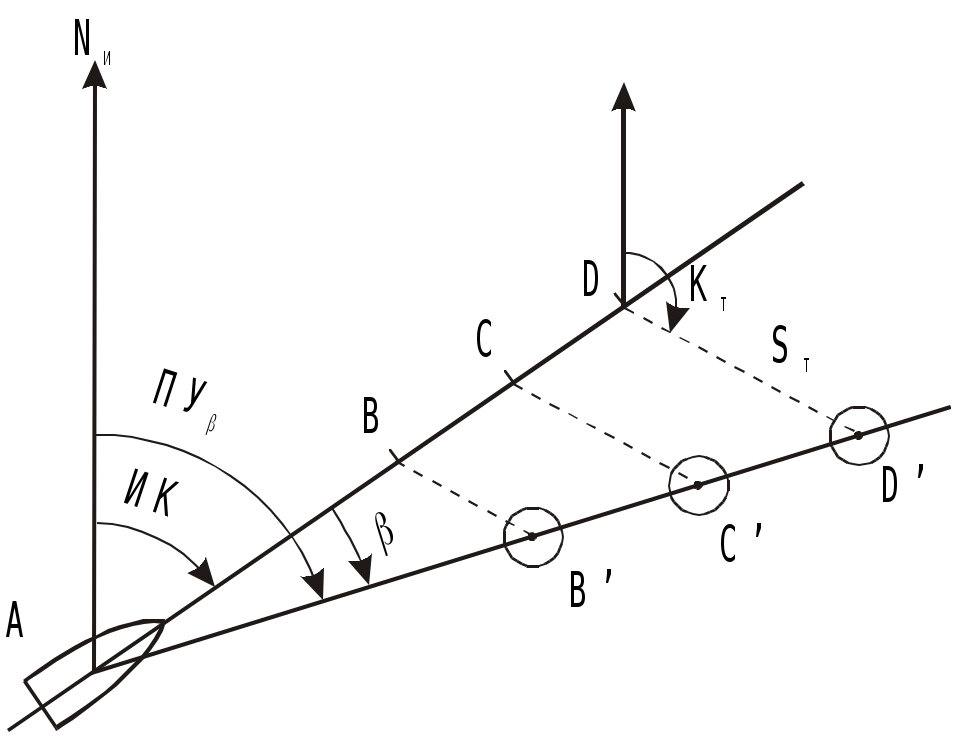
Рис. 4.24. Определение элементов течения по серии обсерваций
ведения о течениях приводятся в Атласах течений, Атласах физико-географических данных, на морских навигационных картах, в лоциях и в таблицах приливо-отливных течений. Во многих пособиях приводятся средние данные о течениях за многолетний период наблюдений. Они оправдываются при многократных переходах большого числа судов. Для конкретного перехода конкретного судна, течения могут отличаться от указанных в пособиях. Поэтому наиболее достоверным способом определения элементов течения в фактическое время плавания является навигационный способ, сущность которого заключается в сравнении счислимых и обсервованных мест судна (рис.4.24). Точки В, С и D - счислимые места судна, точки В, С и D обсервованные места судна в эти же моменты. Соединив обсервованные места судна, получим линию пути АВСD. Направление пути ПУ_ и направление течения К_т снимаются с карты. Скорость течения определяется по формуле _т = DD / t = S_т / t, где S_т - снос судна течением за время плавания t от А до D. Элементы течения навигационным способом можно получить только при отсутствии ветра. При наличии еще и дрейфа от ветра полученные направление и скорость будут элементами суммарного сноса.

Надписи на карте производятся по возможности над линией пути, а если нельзя над линией пути, то под линией пути и параллельно ей. Аналогично надписи при учёте дрейфа; надпись над линией пути при учёте течения состоит из ГКК,  ГК, КК, МК и угла  с его знаком. У счислимого места на линии пути пишется время и отсчёт лага (см. рис.4.23).