вся навигация 2. Счисление пути судна

• Название: Счисление пути судна
• Дата: 31.01.2023
• Размер: 2.02 Mb.
• Имя файла: вся навигация 2.doc
• Тип: Решение; #914065
• страница: 5 из 7

Пример. С судна, следующего ИК = 34 через промежутки времени t₁ = 24 мин 03с и t₂ = 25 мин 59c измерены пеленга на буровую вышку не нанесённую на карту: ГКП₁ = 314, ГКП₂ = 282 и ГКП₃ = 256 (ГК = 0). Определить путь судна ПУ_с и суммарный угол сноса с.

1. 
   От произвольной точки М (рис4.30) отложили ОИП₁ = 134, ОИП₂ = 102 и ОИП₃ = 76.
   
2. 
   Переведя t₁ и t₂ в секунды и приняв коэффициент k = 0,01, получили k t₁ = 14,43 и k t₂ = 15,59, отложили эти величины в сантиметрах или милях по линии ИК от первого пеленга (точка а). Из полученных точек в и с провели линии параллельные ОИП₁ и соединили точки В и С линией пути ПУ_с = 28. Суммарный угол сноса с = 28  34 = 6.
   

Если при выполнении этого способа пеленга берутся до неподвижного ориентира и прокладываются на карте непосредственно от ориентира, нанесенного на карту, то получают фактическую линию суммарного пути, по которому следует судно,, ПУ_с, и суммарный угол сноса с = ПУ_с  ИК.

Если же пеленга прокладываются от точки, изображающей ориентир, нанесенный на любом свободном месте карты, то получают линию параллельную линии суммарного пути ПУ_с и суммарный угол сноса с = ПУ_с  ИК.

Если же пеленга берутся до свободноплавающего ориентира, то определяется только линия пути при дрейфе ПУ_ и, соответственно, угол дрейфа  = ПУ_  ИК. Влияние течения практически исключается.

Точность графического счисления

Возможные погрешности в элементах счисления, углах дрейфа и сноса, поправках компаса и лага, а также в графических построениях на карте, которые накапливаются, приводят к тому, что при ведении прокладки действительное место судна не совпадает с нанесённым на карту счислимым местом. Судоводитель должен уметь оценить точность графического счисления. Погрешности счисления разделим на две группы: погрешность в определении пути судна и погрешность в пройденном расстоянии. Погрешностями графических построений пренебрегаем ввиду их малости.

С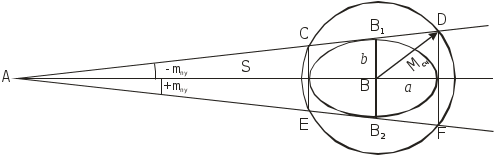
Рис. 4.33. Погрешность счисления за время плавания по счислению
удно следует из точки А в точку В (рис.4.33). Погрешности в определении пути вызовут смещение на величину b, а погрешности в пройденном расстоянии вызовут смещение от точки В на величину а. Погрешности b и а вызваны средними квадратическими погрешностями m_пу, m_л и m_s и поэтому являются средними квадратическими продольными и поперечными погрешностями счисления. Таким образом, возможное место нахождения судна будет в фигуре СВ₁DFВ₂Е, которую можно характеризовать эллипсом с полуосями а и b. Этот эллипс называется средним квадратическим эллипсом погрешности счисления за время плавания по счислению. В практике судовождения эллипс часто заменяется окружностью с радиусом , называемым радиальной средней квадратической погрешностью счисления за время плавания по счислению.

Значение величины b получим из АВ₁В:

, (4.53)

где m_пу - средняя квадратическая погрешность суммарного путевого угла, град.

Величина а зависит от погрешностей в принятом значении поправки лага и от погрешностей в пройденном расстоянии, вызванных неучётом течения или учётом недостоверного течения.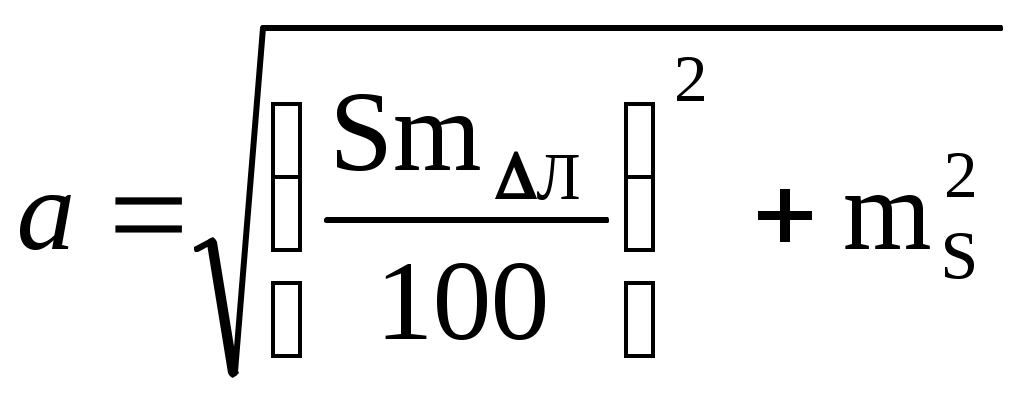

_. (4.54)

При отсутствии ветра и течения m_пу = m_к - средней квадратической погрешности курса, вызванной в основном погрешностью в поправке компаса.

Средняя квадратическая погрешность счисления при отсутствии внешнего воздействия (ветра и течения) зависит только от погрешностей в поправках лага и компаса: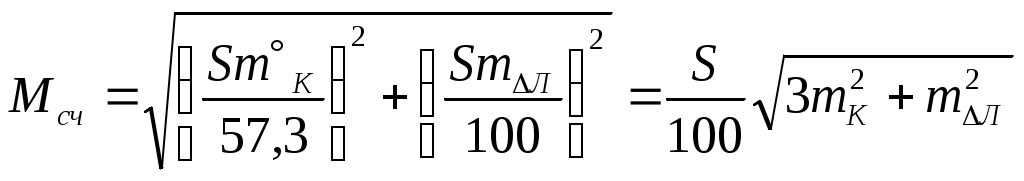

. 4.55)

При учёте дрейфа в формуле (4.55) вместо m_к будет , где m_ - средняя квадратическая погрешность в учёте угла дрейфа, которую можно принять .

При наличии течения средняя квадратическая погрешность в учёте угла сноса от течения m_ = f(V, m_v, P, _т) и может достигать нескольких градусов. Целесообразно учитывать её максимальное значение.

Формулы для вычисления погрешностей m_ и m_s от действия течения могут быть получены из формул аналитического учёта течения

1. 
   ,
   
2. 
   V = V_л cos + _т cos P.
   

Cчитая, что sin    arc1 и продифференцировав уравнение (1) по переменным _т и Р при V_л - cоnst, получим

, (4.56)

где m_p- cкп направления течения, радианы, m_т - скп в учёте скорости течения, узлы.

При Р = 90

. 4.57

В уравнении (2), полагая  = 0, после дифференцирования получим

. (4.58)

При Р = 0

. (4.59

Среднее значение погрешности в скорости неизвестного течения принимается равным: 0,5 - 1,0 уз в районах со значительными приливо-отливными течениями; 0,3 - 0,5 уз в районах открытого моря, где по данным пособий течение отсутствует; 0,2 - 0,3 уз в прибрежной зоне; ветровое течение обычно не превышает 0,3 уз.

При совместном учёте дрейфа от ветра и сноса течением формула (4.53) после подстановки в неё выражения (4.56) примет вид

. 4.60

Если течение не учитывается (_т = 0), но оно может быть, то самый неблагоприятный случай будет при Р = 90: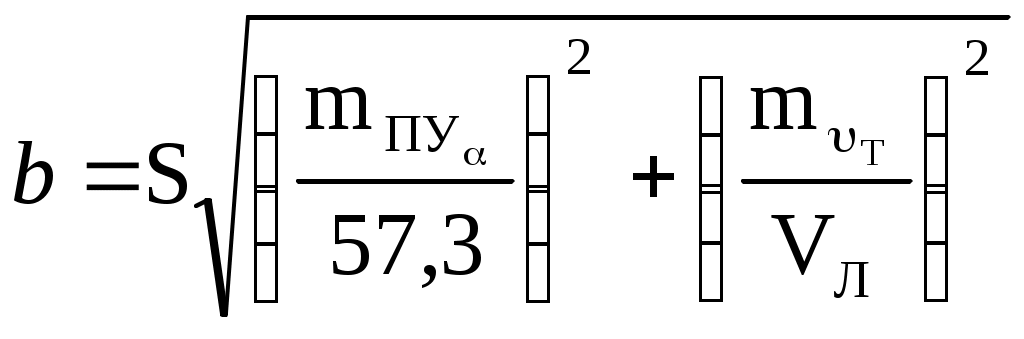

(4.61)

Формула (4.54) после подстановки m_s = m_v t примет вид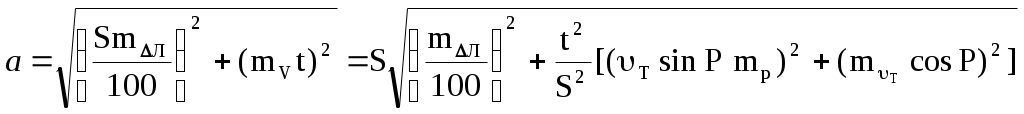

. 4.62

Если течение не учитывается, но оно может быть, то самый неблагоприятный случай будет при Р = 0: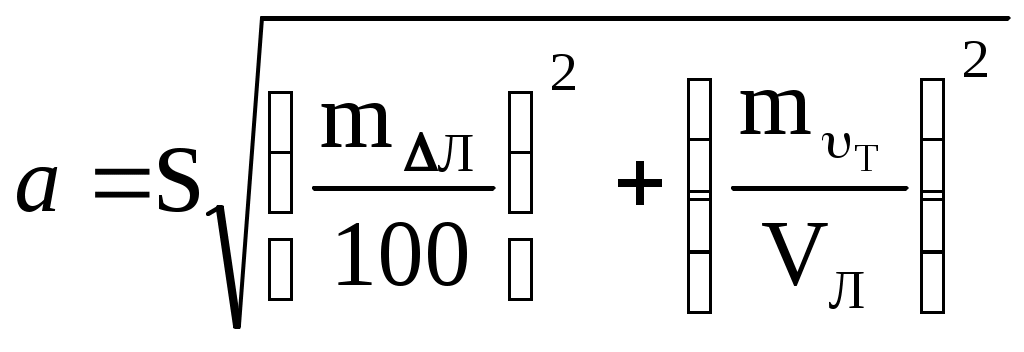

. 4.63

Приближённые значения скп счисления М_сч по многолетним наблюдениям для нормальных условий плавания в зависимости от пройденного расстояния: без ветра и течения М_сч = 0,02S, с учётом дрейфа М_сч = 0,03S; с учётом дрейфа и сноса течением М_сч = (0,03 - 0,07) S.

При плавании несколькими курсами скп счисления в конечной точке М_сч определяется по формуле (рис.4.34):

, (4.64)

где М_{сч к} - средняя квадратическая погрешность счисления в конечной точке плавания по счислению; ΣS=S₁+S₂+…+S_n – сумма плавания по счислению на всех курсах.

Погрешность счисления можно рассчитать и статистическим методом. Экспериментально установлено, что средняя квадратическая погрешность счисления при интервалах счисления t  2 ч. изменяется по линейному закону

М_сч = 0,7 К_сч t, (4.65)

а при интервалах счисления t  2ч - по параболическому закону

, (4.66)

где М_сч - скп счисления в милях, t - интервал счисления в часах, К_сч- коэффициент точности счисления, зависящий от района плавания, степени изученности течений, гидрометеорологических условий плавания, типа судна, состава его технических средств судовождения и точности учёта элементов счисления. По формулам (4.65) и (4.66) составлена таблица 4.9а МТ – 2000.

Коэффициент точности счисления можно рассчитать, если при плавании по одному маршруту собрать данные о невязках между счислимыми и обсервованными местами. Обсервации должны быть равноточными и производиться через примерно равные интервалы времени. Для определения К_сч со скп 10% надо иметь не менее 50 невязок.

При интервале счисления t  2 ч коэффициент точности счисления рассчитывается по формуле

, .67)

при t  2 ч

, (4.68)

где С_i - невязки с интервалом t_i  2 ч, а n₁ - число таких невязок; С_j - невязки с интервалом t_j  2 ч, а n₂ - число таких невязок.

Коэффициент точности счисления может быть предвычислен априорно по формуле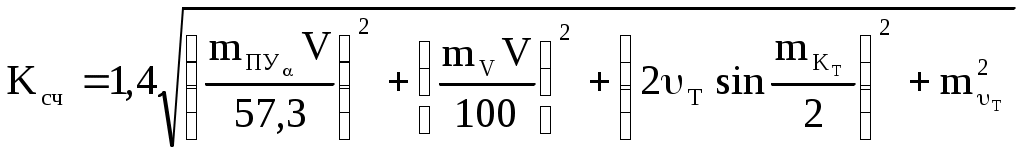

, 4.69)

где , , , - предполагаемые средние квадратические погрешности в пути судна, его скорости и элементах течения.

Если счисление велось от обсервованной точки, то средняя квадратическая погрешность счислимого места (М_c) определяется как квадратичное суммирование средней квадратической погрешности исходной обсервации (М_о) и средней квадратической погрешности счисления в конечной точке после обсервации
(М_{cч к}=М_{сч 0-n})

_{. ,} (4.70)

где М_{сч к} рассчитывается по формулам 4.64, 4.65, 4.66

По формуле (4.70) составлена таблица 4.9б МТ – 2000. СКП М_cч и М_c можно также определить по номограммам 4.10.1 и 4.10.2.

Если после длительного перехода нет возможности получить надёжную обсервацию, а необходимо пройти какой-либо пролив, подойдя к нему только по счислению, надо проложить линию курса из счислимой точки D и две линии параллельные линии курса из двух точек окружности радиуса М_к (рис.4.34). Такая прокладка называется тройной. Для получения предельных погрешностей с вероятностями Р = 95% и Р = 99% следует радиус М_с увеличить соответственно в 2 и 3 раза. Решение вопроса о возможности прохода узкости в отсутствии надёжной обсервации должно определяться свободным прохождением узкости полосой площади вероятного места судна.

Ф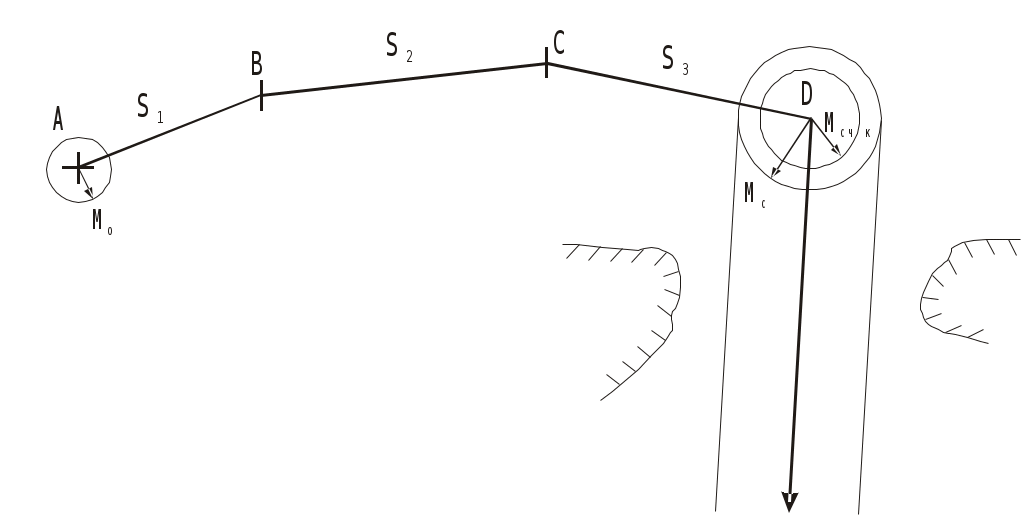
Рис. 4.34. Погрешность счисления при плавании несколькими курсами (М_сч-к), погрешность счислимого места в конечной точке (М_с) и тройная прокладка
ормулы точности графического счисления позволяют судоводителю только ориентировочно оценить погрешность счислимого места судна. Для контроля счисления надо использовать все технические средства судовождения с целью получения надёжной обсервации.

Аналитическое счисление

Формулы аналитического счисления

Кроме графического счисления учёт движения судна может производиться по формулам аналитическим методом. Аналитическим счислением называется вычисление приращений к исходным координатам за счёт движения судна для получения счислимых координат на заданный момент времени.

Аналитическое счисление применяется:

1. 
   при плавании вдали от берегов, когда ведение прокладки на мелкомасштабных картах будет неточным из-за больших погрешностей графических построений;
   
2. 
   при решении астрономических задач для вычисления счислимых координат;
   
3. 
   при вычислении обсервованных координат при разновременных линиях положения для приведения их к одному моменту.
   

К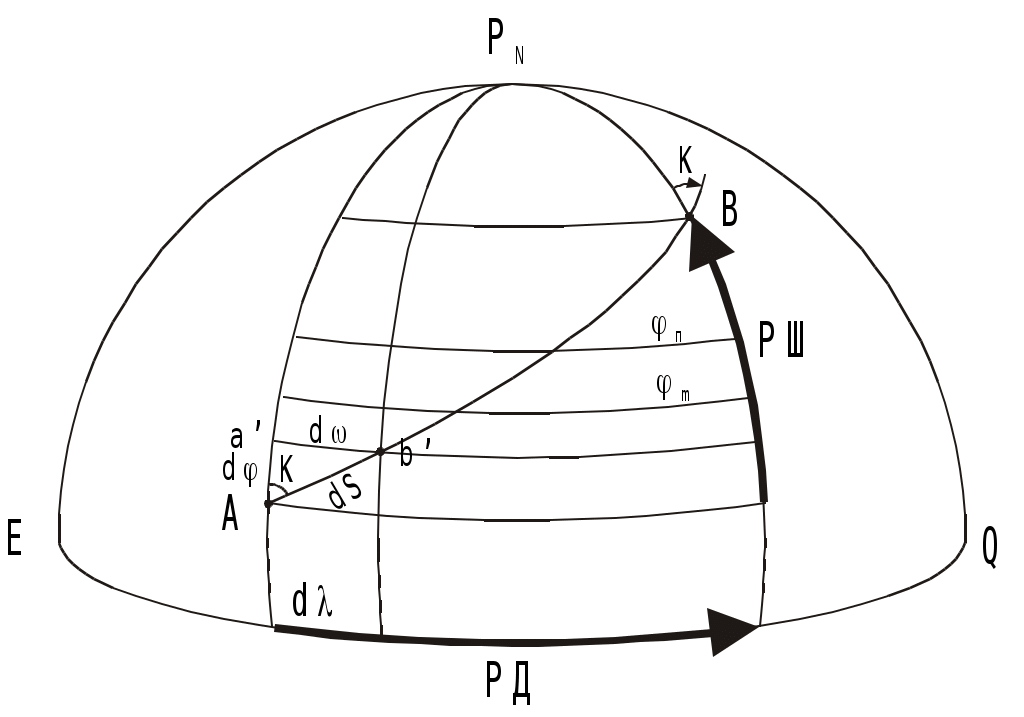
Рис. 4.35. Разность широт и разность долгот
роме того формулы аналитического счисления заложены во все автоматические счислители координат и путепрокладчики.

Выведем основные формулы аналитического счисления.

Судно вышло из пункта отхода А с известными координатами ₁, ₁ (рис.4.35) и, следуя постоянным курсом К по локсодромии, пришло в пункт прихода В с координатами ₂, ₂. Если будут известны сделанные судном РШ и РД, то координаты пункта В получим из соотношений

₂ = ₁ + РШ и (4.71)

₂ = ₁ + РД. (4.72)

Значения РШ и РД можно рассчитать по известным элементам движения: К -курсу судна и S - расстоянию, пройденному судном. Примем Землю за сферу и рассмотрим элементарный Аa b:

Аа = d, Ab = dS и a b = d cоs = d,

где d - расстояние между меридианами по параллели от точки а до b, мор. мили; dS - расстояние, пройденное судном по локсодромии между точками А и b, мор.мили; d - разность широт, мор.мили.

Считая элементарный Аa b плоским, напишем дифференциальные уравнения: d = dS cos K и d = dS sin K.

В результате интегрирования при К = const получим ,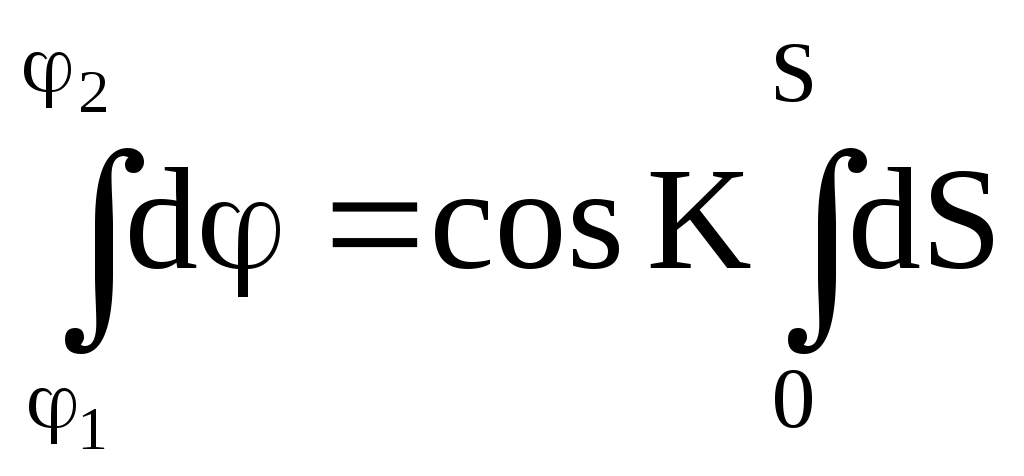

₂  ₁ = S cos K или РШ = S cos K. (4.73)

Для интегрирования d сos необходимо использовать теорему о среднем значении интеграла, вынеся cos за знак интеграла и отнеся его к параллели некоторой промежуточной широты _п: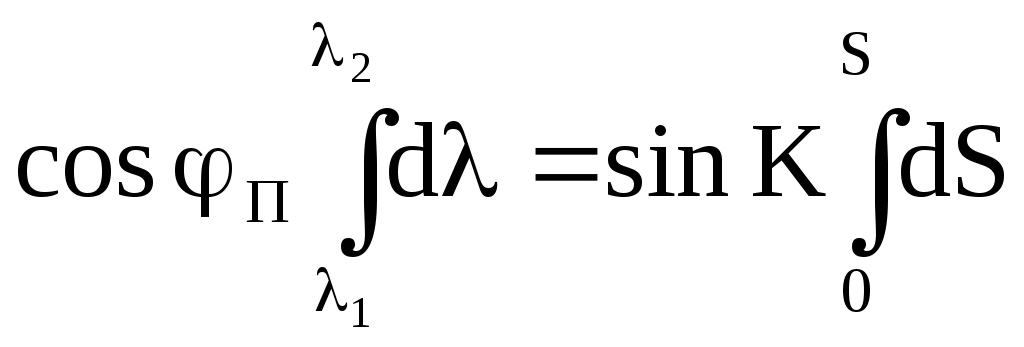

,

(₂  ₁) сos _п = S sinK.

Обозначим (₂  ₁) сos _п =  и назовём эту величину отшествием (ОТШ). Тогда

ОТШ =  = S sin K. (4.74)

В геометрическом смысле ОТШ это отрезок параллели некоторой промежуточной широты _п, заключённый между меридианами пунктов отхода и прихода, выраженный в морских милях.

Уравнение локсодромии для Земли - сферы

РД = tgК РМЧ. (4.75)

Для вывода прямой связи между ОТШ и РД снова воспользуемся теоремой о среднем значении интеграла:

ОТШ = РД cos_п,

откуда РД = ОТШ sec_п. (4.76)

Из формулы (4.76) найдём значение промежуточной широты sec _п = РД / ОТШ. Подставим значение РД и ОТШ из формул (4.75) и (4.74), получим

. (4.77)

И тог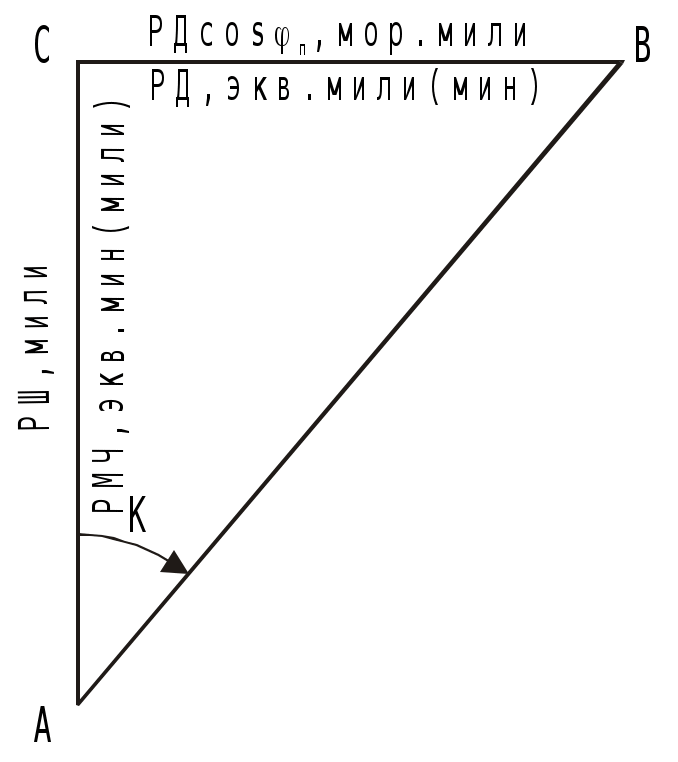да . (4.78)

Т
Рис. 4.36. Решение прямоугольного треугольника
аким образом ОТШ, вычисленное по формуле (4.74), есть длина параллели в морских милях между меридианами точек А и В, широта которой определяется соотношением

.

На коротких переходах можно считать, что в интервале от ₁ до ₂ значение cos изменяется линейно, тогда



Тогда приближённая формула РД будет

РД = ОТШ sec _m. (4.79)

По формулам (4.73) и (4.74) составлена таблица 2.19а “Разность широт и отшествий“ в МТ – 2000. В ней по пройденному расстоянию S от 0 до 100 миль и курсу через 1 выбирают значения РШ и ОТШ. Курсы первой четверти (NE) выделены и напечатаны жирным шрифтом, а рядом даны три курса остальных четвертей, которым соответствуют синусы и косинусы первой четверти. Значения РШ и ОТШ даны в таблице до сотых долей мили и поэтому могут быть использованы с достаточной точностью для плавания в 10 и 100 раз больших чем S. Таблица даёт решение прямоугольного треугольника по гипотенузе (локсодромии) и прилежащему к ней углу (курсу судна - К) (рис.4.36). Проекции локсодромии на меридиан и параллель могут быть выражены в морских милях или экваториальных милях.

Таблица 2.20 МТ – 2000 “Разность долгот”, составленная по формуле РД = ОТШ sec, даёт или приближённое или точное значение РД, в зависимости от того с каким значением широты - средней (_m) или промежуточной (_п) входят в таблицу. Если в таблицу войти с точным значением _п, то получат точное значение (для Земли - сферы) РД, если с приближённым значением _m, то получат приближённое значение РД. В таблице даны результаты вычислений для ОТШ в 1,2....9 и100 миль и для широт от 0 до 90.

Для получения РД двух пунктов для десятков и сотен миль отшествия надо просто перенести запятую, отделяющую целую часть от дробной в выбранных из таблицы значений.

Для учёта сфероидичности Земли в разности широт (РШэ) следует по средней широте выбрать из таблицы 2.19б МТ – 2000 коэффициент f и рассчитать РШэ по формуле

, (4.80)

где РШш – разность широт для шара, выбранная из таблицы 2.19а МТ – 2000.

С учетом сфероидичности Земли РДэ может быть рассчитана по формуле

, (4.81)

где РМЧэ – для земного эллипсоида, выбранная из таблицы 2.28а МТ – 2000, а РШш и ОТШш – для земного шара, выбранные из таблицы 2.19а.