вся навигация 2. Счисление пути судна

• Название: Счисление пути судна
• Дата: 31.01.2023
• Размер: 2.02 Mb.
• Имя файла: вся навигация 2.doc
• Тип: Решение; #914065
• страница: 4 из 7

Учёт приливо-отливного течения

Скорость и направление приливо-отливных течений меняются непрерывно, а также от места к месту. Поэтому при счислении делается допуск о постоянстве таких течений в течение одного часа. В открытых морях приливо-отливные течения имеют замкнутые орбиты и, как правило, при ведении счисления не учитываются. Вблизи берегов и в узкостях скорости приливо-отливных течений могут достигать больших значений и их необходимо учитывать, чтобы предотвратить снос в опасные для плавания районы. Сведения о приливо-отливных течениях помещаются непосредственно на навигационных картах, в специальных атласах или в таблицах и приведены к моменту полной воды в основных пунктах, относительно которых произведены расчёты. Поэтому для выборки данных о течении надо знать время прохождения конкретного района с точностью 30 минут. Рассчитывается положение заданного времени плавания по судовым часам относительно момента наступления ближайшей полной воды в основном пункте. Для учёта приливо-отливного течения необходимо составить таблицу водного времени (табл.4.2). Так, если, например, Т_пв = 11ч.20 мин, то 1 час до полной воды (водный час  ) соответствует промежутку времени от 09ч.50 мин до 10 ч.50 мин (Т_ср = 10ч .20 мин); 1 час после полной воды (водный час + ): от 11ч. 50 мин. до 12ч.50 мин. (Т_ср = 12ч.20 мин.); 2 часа после полной воды (водный час + ): от 12ч.50мин до 13ч.50мин (Т_ср = 13ч.20мин) и т.д.

В атласах и таблицах приводят две скорости течения - сизигийную и квадратурную. Приближённо сизигийными считаются течения за два дня до новолуния и полнолуния и два последующих дня , а квадратурными - за два дня до первой и третьей фазы Луны и два последующих дня. В остальные дни течения считаются промежуточными и скорость их принимается как средняя арифметическая. Фазы или возраст Луны на данные сутки определяются по Морскому Астрономическому Ежегоднику.

Таблица 4.2

Время плавания Тсрi	Время ПВ в основном пункте Тпв	Водный час ТсрiТпв	Направление течения Кт	Скорость течения т
Тср1 Тср2			Кт1 Кт2	т1 т2
Тсрi			Ктi	тi

При учёте приливо-отливного течения решаются те же две задачи, что и при учёте постоянного течения. При прямой задаче постоянным будет ГКК, а, следовательно, и ИК, а ежечасно будет меняться ПУ_, т.к. ежечасно будут меняться элементы течения. А при обратной задаче постоянным будет ПУ_ , а ежечасно будет меняться ИК, а следовательно и ГКК.

П
Рис. 4.25. Учет приливо-отливного течения при прокладке
ри плавании вдали от берегов в районах, где нет навигационных опасностей вместо того, чтобы откладывать течение каждый час можно найти геометрическую сумму векторов течения за 2 - 4 часа и выполнить прокладку построением двух линий: линии ИК и линии ПУ (рис.4.25).

Всегда надо иметь в виду, что элементы приливо-отливных течений могут под влиянием ветра значительно отличаться от выбранных из пособий. Поэтому при плавании в таких районах надо чаще определять место судна и уточнять из наблюдений действительные элементы приливо-отливных течений.

Расчёт элементов ветровых течений производится по Атласу течений, в котором приведены схемы ветрового течения для различных типов полей ветра (т.е. барических образований). Тип поля ветра сообщается в прогнозе погоды или определяется по синоптической карте. На схему ветрового течения, соответствующую данному типу поля ветра, наносится счислимое место судна и, по ближайшей стрелке на схеме, определяются направление и скорость течения.

При отсутствии Атласа течений скорость ветрового течения можно рассчитать по формуле

, (4.40)

где U - скорость истинного ветра в м/с, которую надо определять 1 - 2 раза каждый час;  - широта места судна.

Время, за которое течение приобретает расчётную скорость называется временем развития и оно зависит от глубины района H и широты места. Время развития ветрового течения при ветре 4 - 5 баллов показано в табл. 4.3.

Таблица 4.3

Н, м	Время развития, часы
25-30 50 100 250-300	1-2 3-4 6-8 10-12

Время затухания после прекращения действия ветра равно времени развития.

Направление ветрового течения в северном полушарии отклоняется вправо от направления истинного ветра на величину около 45, в южном полушарии - влево. В мелководных районах с глубинами менее 50 м угол отклонения принимается равным 20 - 25.

Если ветер действует длительное время, ветровое течение необходимо учитывать при ведении счисления и анализе невязок.

Аналитический учёт течения

В автоматических счислителях координат используется аналитический учёт течения, который позволяет выбрать из таблиц угол сноса  и коэффициент k. Угол  используется для расчёта ИК или ПУ_ в формулах (4.36) и (4.37), а коэффициент k для расчёта путевой скорости

V = Vл k (4.41)

и пройденного расстояния по линии пути

S = S_л k = РОЛ К_л k. (4.42)

При аналитическом учёте течения решаются те же две задачи.

П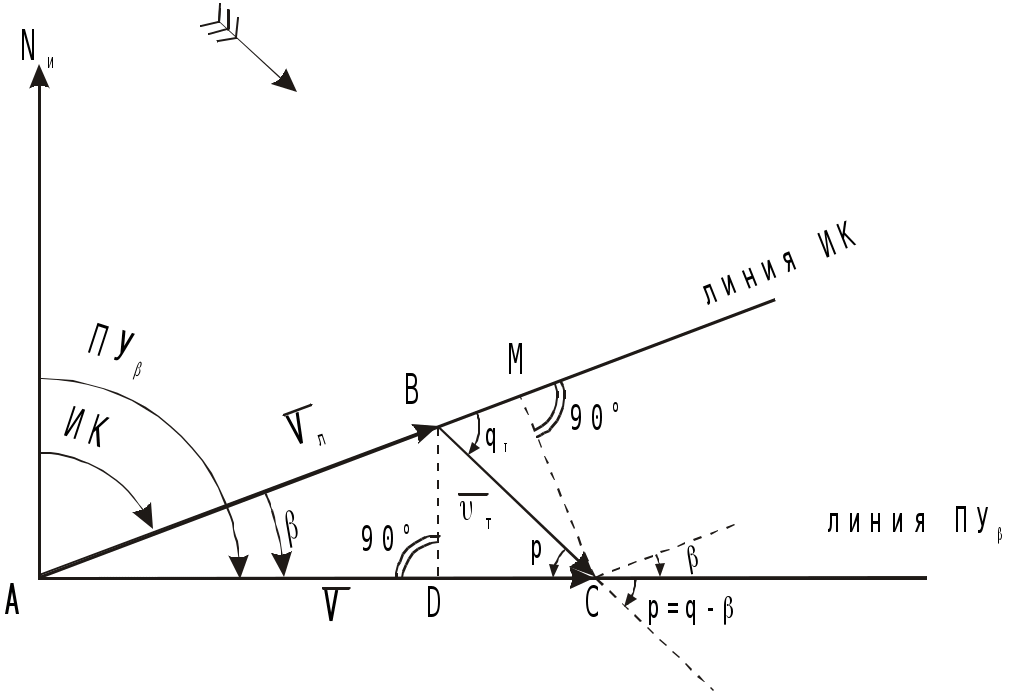
Рис. 4.26. Треугольник скоростей и его проекции на линии ИК, ПУ и на линии перпендикулярные ИК и ПУ
рямая задача. Даны ИК, V_л, К_т и _т. Требуется найти , ПУ_ и V.

Построим треугольник скоростей (АВС) и спроектируем его на линию ИК(АМ) и на линию перпендикулярную ИК (МС) (рис.4.26):

V 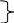cos  = V_л + _т cos q_т;

V sin  = _т sin q_т, ^(4.43)

где q_т = К_т  ИК.

Разделим оба выражения на V_л: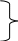

;

,

Обозначим V/ V_л = k и _т / V_л = m и получим два уравнения

k 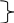cos  = 1+m cos q_т;

k sin  = m sin q_т. ^(4.44)

Для получения  разделим первое выражение на второе:

. (4.45)

Окончательно получим ПУ_ = ИК + ( ).

Для получения k возведём каждый член уравнений (4.44) в квадрат и сложим:

. (4.46)

Путевая скорость V и пройденное по линии пути расстояние S определяются по формулам (4.41) и (4.42).

По формулам (4.45) и (4.46) составлены таблицы 2.18а и 2.18в МТ – 2000.

Пример 1. ГКК =149, ГК = +1, V_л = 15 уз, К_т =210, _т = 1,5 уз. Определить , ПУ_ и V.

Решение: 1) Вычисление угла q_т и отношения скоростей m:

ИК = ГКК + ГК = 149 + (+1) = 150, q_т = К_т  ИК =210 150 = +60

m = _т / V_л = 1,5 / 15 = 0,1.

2) Вычисление угла :

,  = 4,7

3) Вычисление коэффициента k:



4) Вычисление ПУ_ и V:

ПУ_ = ИК+ () = 150+4,7 = 154,7, V= V_л k= 151,0536 = 15,8 уз.

Обратная задача. Даны ПУ_, V, К_т, _т. Требуется найти , ИК и V.

Спроектируем треугольник скоростей (АВС) на линию пути (АС) и линию перпендикулярную пути (BD) (рис.4.26):

V 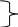=V_л cos  + _т cоs P;

V_л sin = _т sin P, ^(4.47)

где Р = К_т - ПУ_.

Разделим второе уравнение на V_л:

sin  = m sin P. (4.48)

Окончательно получим ИК = ПУ_  ( ).

Рассчитав q_т = P + , по формуле (4.46) находят k и получают V и S по формулам (4.41) и (4.42).

По формуле (4.48) составлена таблица 2.18б МТ – 2000.

Пример 2. Задан ПУ_ = 220, V_л =10 уз, К_т =260, _т = 2 уз, ГК = + 0,5. Определить ГКК, которым надо следовать,  и V.

Решение: 1) Вычисление угла Р и отношения скоростей m:

Р = К_т  ПУ = 260  220 = 40

m= _т / Vл = 2 : 10 =0,2

2) Вычисление угла :

sin  = m sin P = 0,2  0,64279 = 0,12856,  = + 7,4

3) Вычисление угла q_т и коэффициента k:

q_т = Р +  = 40 + (+ 7,4) = 47,4



4) Вычисление ИК, ГКК и V:

ГКК = ПУ_  ( )  ГК = 220  (+ 7,4)  (+ 0,5) = 212,1

V = V_л k = 10  1,1448 = 11,4 уз.

Совместный учёт ветра и течения.

Е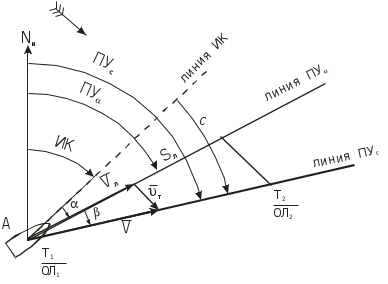
Рис. 4.27. Прямая задача при совместном учете ветра и течения
сли на судно одновременно действуют и течение и ветер, то при совместном их учёте следует различать два случая: первый - когда известны угол дрейфа и элементы течения (рис.4.27), и второй - когда известен только суммарный угол сноса, равный алгебраической сумме

с =  +. (4.49)

Если суммарный угол сноса вправо, то он имеет знак “+”, если влево, то – знак “”. В обоих случаях решаются две задачи : прямая и обратная.

Первый случай: известен  и К_т, _т.

Прямая задача. Первым учитывается дрейф, а затем течение. На карте коротким отрезком прокладывается линия ИК, затем линия ПУ_ (рис.4.27). Далее строится навигационный треугольник: на линии ПУ_ откладывается вектор скорости судна по лагу V_л в выбранном масштабе, из конца которого откладывается вектор скорости течения _т. Соединив начальную точку А с концом вектора течения, получают линию пути при суммарном действии ветра и течения ПУ_с и вектор путевой скорости судна V.

Для нахождения счислимой точки на заданный момент времени пройденное расстояние по лагу S_л откладывается по линии ПУ_ и переносится по направлению течения на линию суммарного пути ПУ_с. Если угол дрейфа   6, то либо проводят линию ИК полностью, а не отрезком и, отложив по ней S_л = РОЛ Кл, переносят полученную точку перпендикулярно линии ИК на линию ПУ_ , либо откладывают на линии ПУ_ расстояние S = S_л sec . И уже эту точку с ПУ_ переносят по направлению течения на линию суммарного пути ПУ_с.

О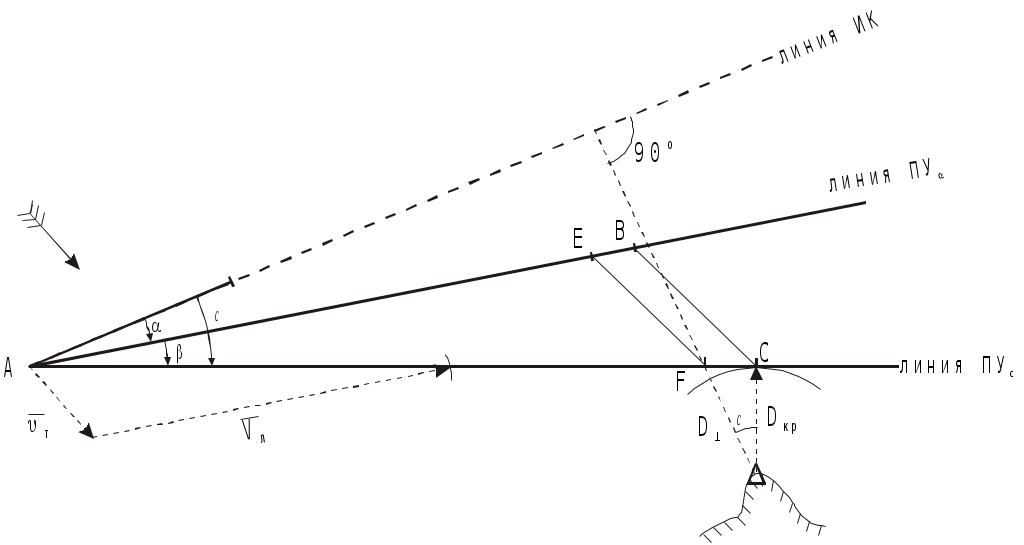
Рис. 4.28. Обратная задача, кратчайшее расстояние и траверз при совместном учете ветра и течения
братная задача. Первым учитывается течение, а затем уже дрейф. Из начальной точки А, проложенной на карте линии пути ПУ_с, проводят вектор скорости течения _т, из конца которого радиусом равным V_л делается засечка на линии пути (рис.4.28). Полученное направление переносят в начальную точку и получают линию ПУ_. Далее коротким отрезком проводят линию ИК = ПУ_  .

Чтобы определить Т и ОЛ в момент кратчайшего расстояния надо D_кр отложить до линии ПУ_с и полученную точку С перенести на линию ПУ_ в точку В по направлению обратному направлению течения (см. рис.4.28). Отрезок АВ равен S_л. Зная V_л и К_л рассчитывают ОЛ_в =ОЛ_а + S_л / К_л и Т_в = Т_а+S _л / V_л.

Для расчёта отсчёта лага момента времени прихода ориентира на траверз судна надо рассчитать ИП_ = ИК  90 и провести от ориентира ОИП_ до пересечения с линией ПУ_с. Полученную точку F перенести на линию ПУ_ в точку Е по направлению обратному направлению течения. Отрезок АЕ равен S_л. Аналогично расчёту ОЛ и Т в момент D_кр рассчитывают траверзные ОЛ_ и Т_. Угол между D_ и D_кр будет равен суммарному углу сноса с.

Второй случай: известен только суммарный угол сноса с. В этом случае на карте прокладываются две линии: ИК и ПУ_с и также решаются прямая и обратная задачи аналогично как и в первом случае, только при прямой задаче из конца вектора скорости судна по лагу V_л, откладывается вектор суммарного сноса _с. Соединение начальной точки с концом этого вектора даёт линию пути при суммарном действии ветра и течения ПУ_с и вектор путевой скорости V.

При обратной задаче из начальной точки проложенного на карте пути ПУ_с, по которому должно следовать судно несмотря на совместное действие ветра и течения, откладывается вектор суммарного сноса _с, из конца которого радиусом равным V_л делается засечка на линии ПУ_с. Отрезок от исходной точки до засечки на линии пути - это вектор путевой скорости V. Направление полученной линии переносится в начальную точку и представляет собой линию ИК.

Надпись на карте при совместном учете ветра и течения состоит из ГКК, ГК, КК, МК и угла суммарного сноса с с его знаком.

Навигационные методы определения пути судна.

В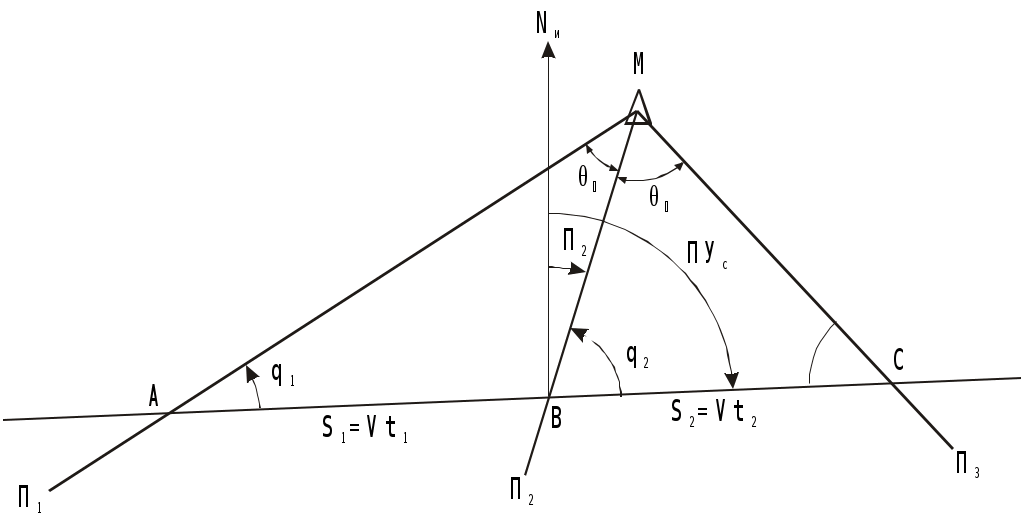
Рис. 4.29. Определение пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
практике судовождения часто судоводитель не знает отдельно каждые из элементов сноса течением и дрейфа от ветра, но может получить путь и суммарный угол сноса самым простым и надёжным способом - по обсервациям (см.п.4.1.4). Именно знание пути и действительной скорости судна относительно Земли является главной задачей судоводителя для обеспечения безопасности судовождения. Если по каким-либо причинам нельзя использовать этот метод, то направление линии пути можно определить по любому неподвижному ориентиру, который даже может быть и не нанесён на карту. Для этого надо трижды измерить пеленга на этот ориентир и как можно точнее измерить промежутки времени между этими пеленгами. Судно при этом должно следовать постоянным курсом и скоростью. Итак, в фиксированные с точностью до секунды моменты времени измеряют три пеленга П₁, П₂ и П₃ любого неподвижного ориентира. Этот способ определения пути основан на том, что любая прямая, пересекающая три пеленга так, что её отрезки между пеленгами относятся как S₁/ S₂ = Vt₁/ Vt₂ = t₁/ t₂, будет параллельна линии пути. Для получения линии пути надо найти угол q₂ (рис.4.29) и, сложив его с измеренным П₂, получить ПУ_с:

ПУ_с = П₂ + ( q₂), (4.50)

q₂ имеет знак “+”, если предмет расположен слева, и знак “” если справа.

Обозначим через t₁ время плавания между первым и вторым пеленгами и через ₁- угол между этими пеленгами; через t₂ - обозначим время плавания между вторым и третьим пеленгами и через ₂ - угол между вторым и третьим пеленгами.

Из  АМВ угол q₂ = q₁ + ₁ как внешний, отсюда q₁ = q₂  ₁.

Из  ВМС угол С =180  (q₂+₂).

Из  АМВ и  ВМС найдём значения ВМ:

, ,

, , т.к. sin(180)=sin.

Следовательно



t₁sinq₂₁ sin₂ = t₂sinq₂+₂ sin₁.

Используя формулы сложения и вычитания синусов

sin(a  b) = sin a cos b  cos a sin b,

получим:

t₁ (sin q₂ cos ₁  cos q₂ sin ₁) sin ₂ = t₂ (sin q₂ cos ₂+ cosq₂ sin₂) sin₁.

Разделим каждое слагаемое на sinq₂ sin₁ sin₂:

t₁ ctg₁  t₁ ctgq₂ = t₂ ctg₂ + t₂ ctgq₂.

Откуда определим

. (4.51)

По формуле (4.50) рассчитаем путь судна.

Если пеленга взяты через равные промежутки времени, то формула (4.51) упростится

. (4.52)

Эта задача имеет и графическое решение (рис.4.30).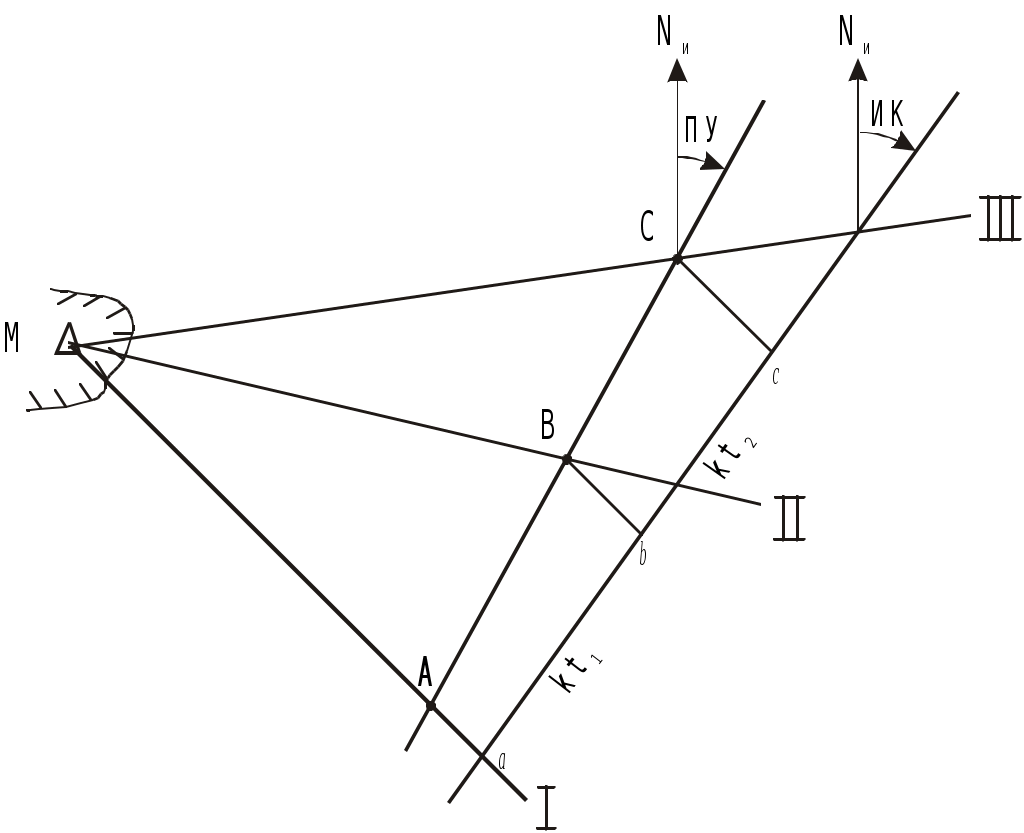

И
Рис. 4.30. Графическое решение задачи определения пути по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
з произвольной точки на свободном месте карты прокладывают 3 измеренных пеленга. Из произвольной точки a на первом пеленге проводят линию ИК (можно и произвольную линию), на которой откладывают отрезки пропорциональные времени плавания: kt₁из точки а и kt₂ из точки в (k -произвольный коэффициент). Из полученных точек в и с проводят линии параллельные первому пеленгу до пересечения их со вторым пеленгом в точке В и третьим - в точке С. Прямая АВС будет параллельна линии пути. Этот приём основан на свойстве параллельных прямых, пересекающих пучок прямых:



Е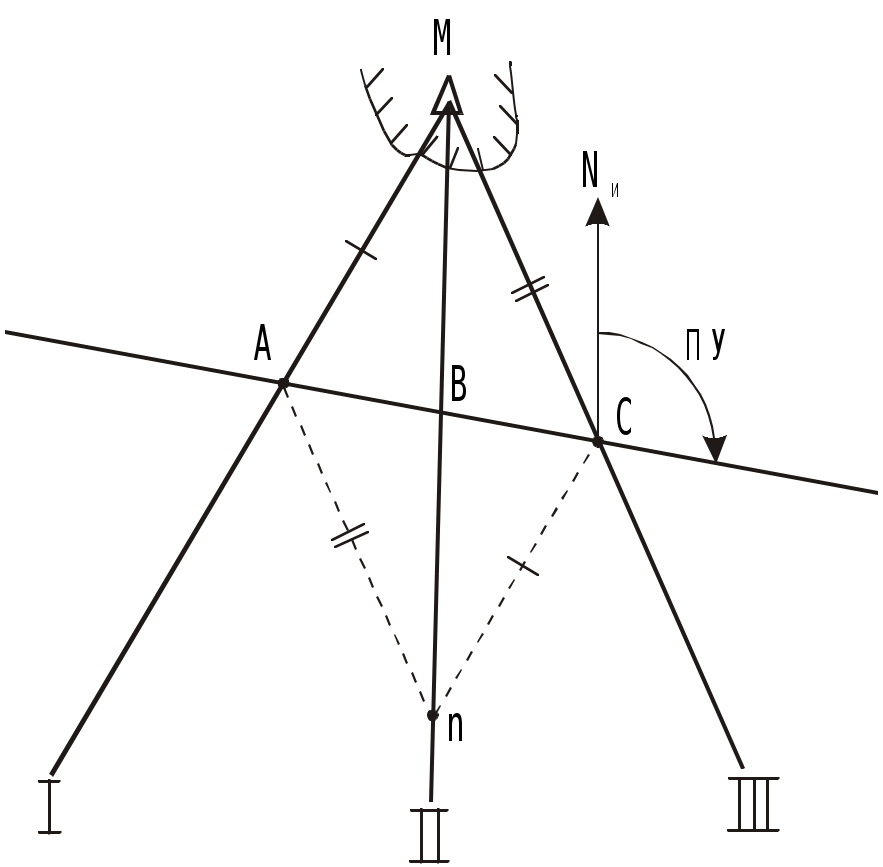


Рис. 4.31. Определение пути по трем пеленгам неподвижного ориентира, взятым через равные промежутки времени
сли пеленга брать через равные промежутки времени, то графическое решение ещё упростится. Из произвольной точки n на втором пеленге (рис.4.31) проводят линии параллельные первому (nС) и третьему (nA) пеленгам. Линия AС будет параллельна направлению линии пути, т.к. на основании свойства диагоналей параллелограмма АВ = ВС, т.е за равные промежутки времени судно проходит равные расстояния.

Графическое решение может быть выполнено и с помощью линейки, на которой отложены отрезки пропорциональные плаваниям S₁ = kt₁ и S₂ = kt₂(точки а, в и с на линейке) (рис.4.32). Линейку надо расположить так, чтобы точки а, b и с лежали соответственно на первом, втором и третьем пеленгах. Прямая, проведённая через эти точки будет параллельна линии пути.

Для повышения точности все графические построения надо делать в возможно более крупном масштабе.

О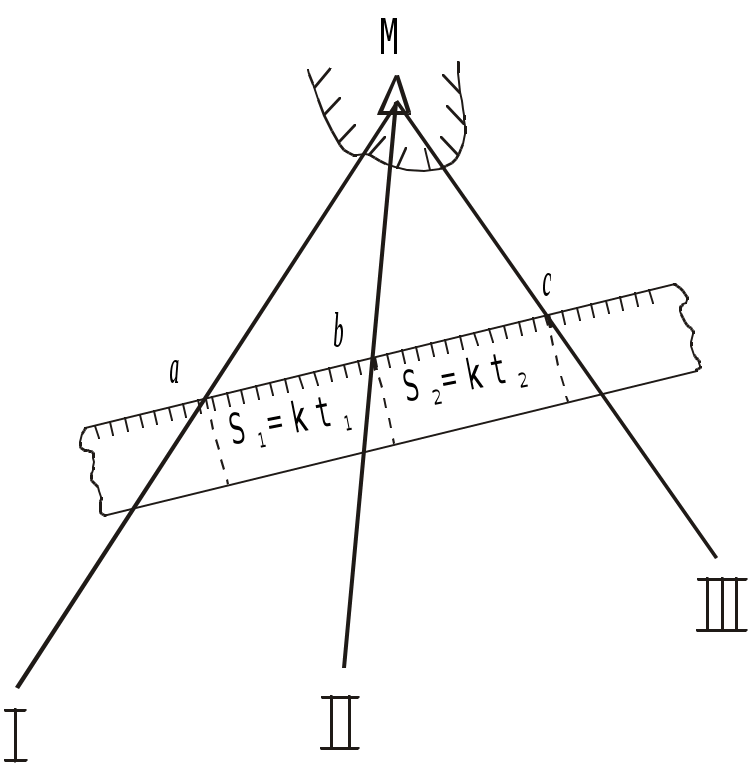


Рис. 4.32. Определение пути с помощью линейки по трем пеленгам неподвижного ориентира и времени плавания между пеленгами
пределение суммарного сноса по пеленгам неподвижного ориентира и времени производится с достаточно высокой точностью, т.к. погрешностями в отсчётах времени t₁ и t₂ при использовании секундомера можно пренебречь, а в формулу расчёта q₂ входят только углы ₁ и ₂, представляющие собой разности пеленгов, т.е. систематические ошибки в пеленгах также не скажутся на точности q₂.

При определении суммарного пути судна по формуле (4.50), если пеленг будет содержать погрешность в поправке компаса, то полученное направление пути также будет содержать эту погрешность. А на величине суммарного сноса эта погрешность не скажется, т.к. угол с получается, как разность ПУ_с и ИК, а ПУ_с и ИК будут ошибочны на одну и ту же величину погрешности в поправке компаса.

На величине q₂ скажутся только случайные погрешности пеленгования, т.к. углы ₁ и ₂ рассчитываются по значениям пеленгов.

При достаточно больших углах ₁, ₂ и m_п =  0,3 случайные погрешности в определении q₂ находятся в пределах  1.