вся навигация 2. Счисление пути судна
 Скачать 2.02 Mb.
|
|
Виды аналитического счисления Табличное аналитическое счисление подразделяется на три вида: простое, составное, и сложное. Простое аналитическое счисление выполняется, когда судно следует одним курсом. По формулам или таблицам вычисляют РШ и РД и получают конечные координаты. Судно из начальной точки c координатами 1 и 1, следуя истинным курсом ИК и, пройдя расстояние S в морских милях, придёт в конечную точку с координатами 2 и 2. Порядок действия следующий. По аргументам ИK и S из табл. 2.19а МТ – 2000 выбирают РШ и ОТШ. Если S более 100 миль, то его значение разбивают на несколько слагаемых равных или менее 100 миль каждое, для которых и выбирают значения РШ и ОТШ и затем суммируют их. При учёте дрейфа вместо ИК аргументом для входа в табл. 2.19а является ПУ = ИК + . При дробном значении ИК (ПУ) следует произвести интерполяцию. Рассчитывают среднюю широту (с точностью до 0,1): m = 1 + РШ/2. По аргументам m и ОТШ из табл. 2.20 МТ – 2000 выбирают РД. Вычисляют координаты конечной точки 2 и 2: 2 = 1 + РШ и 2 = 1 + РД. Составным аналитическим счислением называется счисление при плавании несколькими курсами, или одним курсом, но с учётом течения. В этом виде счисления не вычисляются промежуточные точки, а рассчитываются только координаты точки прихода. Найдя для каждого курса РШ и ОТШ, рассчитывают алгебраическую сумму разностей широт, называемую генеральной разностью широт (Ген РШ) и алгебраическую сумму отшествий, называемую генеральным отшествием (Ген ОТШ) (рис.4.37) Г 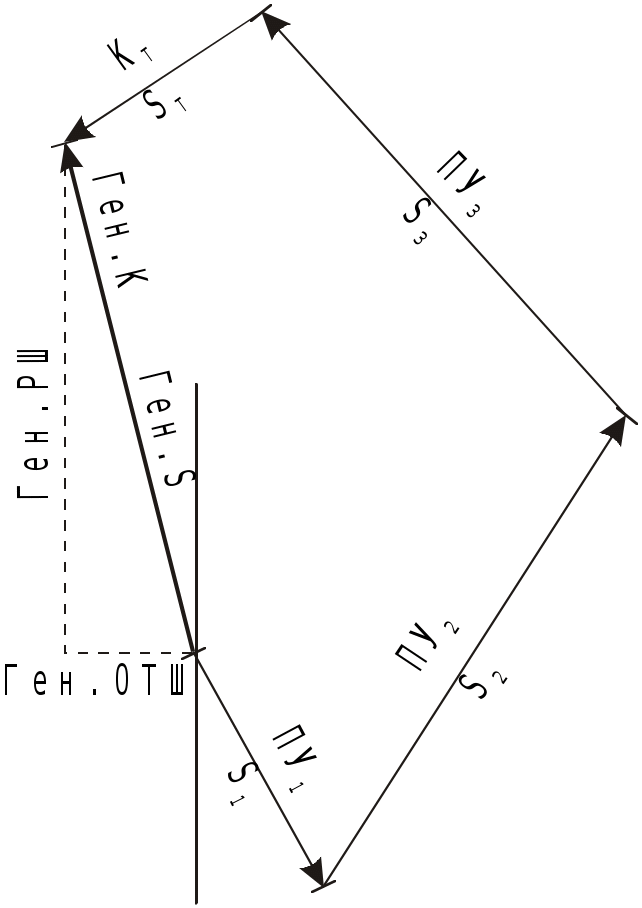 Рис. 4.37. Составное аналитическое счислениеен РШ = РШN(S) РШS(N); Ген ОТШ = ОТШE(W) OТШW(E). По аргументам m = 1 + Ген РШ / 2 и Ген ОТШ из табл. 2.20 МТ – 2000 выбирают РД (РД = Ген ОТШ sеc m), и вычисляют координаты точки прихода 2 и 2: 2 = 1 + Ген РШ и 2 = 1 + РД. Сложным аналитическим счислением называется счисление, при котором для каждого курса рассчитываются не только РШ и ОТШ, но и РД. Алгебраическая сумма разностей долгот называется генеральной разностью долгот (Ген РД): Ген РД = РДE(W) РДW(E). Kоординаты точки прихода вычисляются по формулам 2 = 1 + Ген РШ и 2 = 1 + Ген РД. В составном и сложном аналитическом счислении постоянное течение учитывается, как отдельный курс: направление течение Кт принимается за ИК, а снос течением Sт = Т (t2 -t1) принимается за плавание S. Приливо-отливное течение учитывается или как постоянное - ежечасно, или вычисляется величина суммарного линейного сноса от действия приливо-отливного течения. В этом случае выбирают РШ и ОТШ на каждый час, а затем рассчитывают Ген РШтеч. и Ген РДтеч., характеризующие линейный снос от приливо-отливного течения. Полученными Ген РШтеч. и Ген РДтеч. исправляют, рассчитанные без учёта течения 2 и 2. Циркуляция также учитывается отдельным курсом: за ИК принимается промежуточный курс ИКпр = ИК1 + qпр.к. и за плавание S принимается плавание по промежуточному курсу d. КУ промежуточного курса q и величина d выбираются из таблицы циркуляции. При составном и сложном счислении курс, рассчитанный по Ген РШ и Ген ОТШ, ведущий непосредственно из точки отхода в точку прихода называется генеральным курсом:  , (4.82)а расстояние по генеральному курсу называется генеральным плаванием Ген S = Ген РШ sec Ген К. (4.83) Пример. Выйдя из точки с координатами 1 = 5340,4 N, 1 = 528,3 E, судно совершило плавание переменными курсами. Во время плавания в продолжении 47 часов учитывалось течение на 240 со скоростью 0,9 узла и дрейф от ветра направлением 280. ГК = 0,5. Рассчитать координаты точки прихода, учитывая циркуляцию судна при повороте на второй курс по таблице циркуляции (см. табл. в п.4.1.2). Диаметр циркуляции - 5 кб, руль 30. Рассчитать также генеральный курс и генеральное плавание. Решение: 1. Рассчитывают Ген РШ и Ген ОТШ:
189,14 78,87 88,29 115,37 78,87 88,29 Ген РШ=110,27кN Ген ОТШ=27,08кW 2. Рассчитывают m: 1 = 5340,4 N 1/2 Ген РШ = 55,1 к N  m = 5435,5 N3. Находят Ген РД:
4. Находят координаты точки прихода: 1 = 5340,4 N 1 = 528,3 Е Ген РШ = 150,3 к N Ген РД = 46,7 к W  2 = 5530,7 N 2 = 441,6 Е5. Рассчитывают Ген К и Ген S:  , Ген К= 1347,9 NW = 34612,1346,2Ген S = Ген РШ Sec Ген К = 110,27 1,02971 = 113,546 113,5 мили. Точность аналитического счисления Аналитическое вычисление координат по формулам или таблицам исключает погрешности графических построений на карте, но не исключает погрешностей в поправках компаса и лага, а также погрешностей, вызванных неточным учётом дрейфа от ветра и сноса течением. Поэтому, все, что было сказано о точности графического счисления, полностью относится и к аналитическому счислению, за исключением графических погрешностей при прокладке. Сами формулы аналитического счисления точны в том случае, если Землю принимать за сферу (кроме допуска о замене п через m). Среднюю квадратическую погрешность аналитического счисления можно вычислить по формуле  , (4.84)где mрш - скп в разности широт, mотш - cкп в отшествии. Обе эти погрешности зависят от погрешностей в курсе (пути) - mк и в пройденном расстоянии - ms и получаются дифференцированием основных формул (4.73) и (4.74): 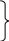  (4.85)  Погрешность от замены п через m сказывается только на долготе и выражается формулой = ОТШ tgm secп sin(п m). (4.86) Расчёты по этой формуле показывают, что замена п через m возможна в широких пределах. Промежуточную широту надо применять при плавании в высоких широтах и только при S более 100 миль. *** В современных приёмоиндикаторах спутниковых и радионавигационных систем выполняется автоматическое обсервационное счисление, базирующееся на непрерывном уточнении счислимых координат по результатам обсерваций. По высокоточным обсервациям вычисляется путь судна и его скорость, а затем эти данные используются для счисления. Точность такого счисления высокая: погрешность составляет десятые доли мили. Крюйс-пеленг и его частные случаи. Способ применяется, когда в видимости имеется только один ориентир. Если судно стоит, то, пеленгуя этот ориентир, будем иметь только одну линию положения (если по какой-либо причине нет возможности определить ещё и дистанцию до него), и место судна в этом случае определить нельзя. Если же судно движется, то ситуация меняется. Если через некоторое время после первого взять второй пеленг, то место судна будет в точке пересечения двух линий положения: второго пеленга и окружности с радиусом D и центром в месте расположения ориентира: 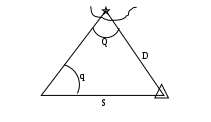  На практике пользуются графическим решением. Ориентир переносят в том направлении и на то расстояние, которое судно прошло между моментами взятия пеленгов, и повторяют проведение первого пеленга через новое место ориентира. Второй пеленг проводят непосредственно от ориентира. Можно также перенести первый пеленг параллельно самому себе в том направлении и на то расстояние, которое судно прошло между моментами взятия пеленгов. Если отсутствуют ветер и течение, это будет выглядеть так: 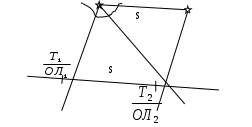 или так: 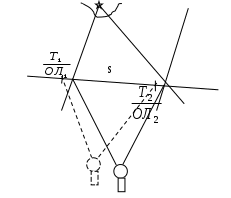 При учёте ветра действуют аналогично, только первый пеленг или маяк переносится на расстояние S или более точно -   в направлении  . При учёте течения или совместном учёте ветра и течения первый пеленг или маяк переносится в направлении 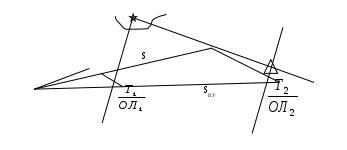 или  соответственно, на расстояние, пройденное по путевому углу: Способ применим и тогда, когда судно между пеленгованиями меняло курс. В этом случае необходимо снести маяк в направлениях, соответствующих курсам на соответствующие расстояния, пройденные каждым курсом: 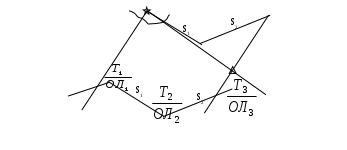 Частные случаи: 1.  1 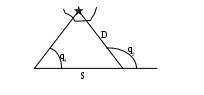  2. Второй пеленг взят на траверзе ориентира.  при  при   .Аналогичный способ определения места можно использовать и с использованием двух ориентиров: когда первый пеленг берётся по одному, а второй – по другому ориентиру. Первый пеленг переносится в направлении ПУ на пройденное по этому ПУ расстояние, а второй проводится непосредственно от второго ориентира. Случайные ошибки при определении места способом крюйс-пеленга. Можно заметить, что для обозначения места, полученного способом крюйс-пеленга, используется специальный значок – треугольник. Это – не случайно. Все ошибки счисления (неточный учёт ветра, течения, ошибки в поправках лага и компаса) входят в полученное место. Для примера можно рассмотреть случай, когда мы не учли течение и снесли пеленг по направлению ИК на расстояние S: 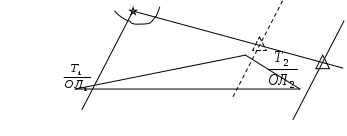 Для уменьшения ошибок необходимо минимальное плавание между пеленгованиями, минимальное расстояние до ориентиров, точный учёт дрейфа и течения. Второй пеленг рекомендуется брать в момент, когда ориентир находится вблизи траверза. Среднеквадратическая погрешность определения места судна этим способом: 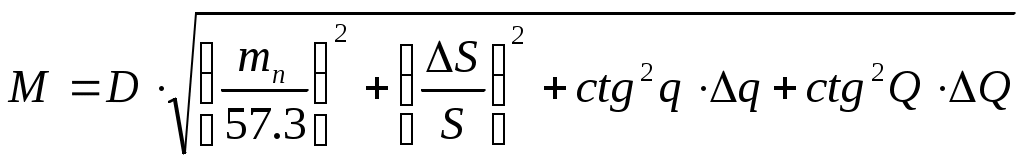 где D – расстояние до ориентира в момент взятия второго пеленга.  - относительная ошибка в пройденном между моментами пеленгования расстоянии. Она может быть вызвана ошибками в поправке лага или ошибками при учёте течения. - ошибка в значении угла между первым пеленгом и линией пути. Может возникать как из-за случайной ошибки в значении пеленга, так и из-за ошибки в значении угла суммарного сноса с. - ошибка в значении угла между пеленгами. Может быть вызвана случайными ошибками пеленгования, а также ошибками в расчёте или прокладке истинных пеленгов.Из формулы следует, что при одинаковых Q и q место судна получается точнее при уменьшении расстояния до ориентира в момент взятия второго пеленга. Котангенсы углов резко увеличиваются при уменьшении угла до 20-25°, поэтому нужно критически относиться к месту судна, если оно получено при таких значениях Q и q. Однако, если значения Q или q близки к 90° 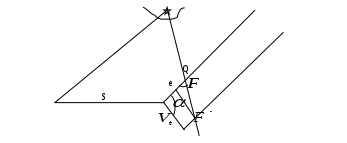, то возрастает величина D и ошибка тоже увеличивается. В целом, место по крюйс-пеленгу наиболее точно определяется при  и  . Наибольшие ошибки возникают из-за неправильного учёта течения. Если мы учитываем течение, то место судна получается в точке  , а если не учитываем – то в точке  .из треугольника  :  Таким образом, получается, что, при   , то есть если направление течения известно и первый пеленг взять приблизительно в направлении течения, то место судна будет свободно от ошибки в учёте течения.Исправленный крюйс-пеленг. Если за время плавания от последней надёжно обсервованной точки его курс, скорость и элементы сноса от ветра и течения не менялись, то линия пути судна проходит через последнюю обсервованную точку, а по трём пеленгам одного ориентира можно получить линию, параллельную пути судна: 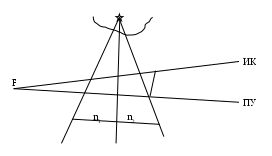 Действуя в соответствии с тем же принципом вмещения пропорциональных пройденному пути отрезков между линиями пеленгов, получим способ определения места судна и линии пути методом исправленного крюйс-пеленга. 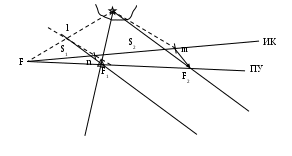 А Для этого от места надёжной обсервации F по истинному курсу отложим расстояния S1 и S2, пройденные по лагу между пеленгованиями и получим точки n и m . Далее соединяем точку m с ориентиром и полученную линию переносим параллельно самой себе в точку n. Через полученную в пересечении этой линии с линией, соединяющей ориентир и надёжную обсервацию точку l, повторяем второй пеленг. Если получившееся место судна соединить с точкой надёжной обсервации, то получим линию пути.   Постоянная ошибка в поправке лага не окажет влияния на окончательный результат, так как при построении используется только отношение пройденных расстояний. Исследование точности этого способа показывает, что в случае постоянства или увеличения элементов сноса исправленный крюйс-пеленг даёт более точный результат, чем обычный. При ослаблении ветра и течения в некоторых случаях обычный крюйс-пеленг - точнее. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||