разработка алгоритмического програмного обеспечения для ранговог. Сегментация изображений огромный шаг для анализа изображений. Она разделяет изображение на составляющие части или объекты. Уровень детализации разделяемых областей зависит от решаемой задачи

• Название: Сегментация изображений огромный шаг для анализа изображений. Она разделяет изображение на составляющие части или объекты. Уровень детализации разделяемых областей зависит от решаемой задачи
• Дата: 17.07.2020
• Размер: 1.43 Mb.
• Имя файла: разработка алгоритмического програмного обеспечения для ранговог.docx
• Тип: Документы; #134485

Введение.

Сегментация изображений — огромный шаг для анализа изображений. Она разделяет изображение на составляющие части или объекты. Уровень детализации разделяемых областей зависит от решаемой задачи. К примеру, когда интересуемые объекты перестают сохранять целостность, разбиваются на более мелкие, составные части, процесс сегментации стоит прекратить. Алгоритмы сегментации изображений чаще всего базируются на разрыве и подобии значений на изображении. Подход разрывов яркости базируется на основе резких изменений значений интенсивности, подобие же — на разделение изображения на области, подобные согласно ряду заранее определенных критериев. Таким образом, выбор алгоритма сегментации изображения напрямую зависит от проблемы, которую необходимо решить. Обнаружение границ является частью сегментации изображений. Следовательно, эффективность решения многих задач обработки изображений и компьютерного зрения зависит от качества выделенных границ. Выделение их на изображении можно причислить к алгоритмам сегментации, которые базируются на разрывах яркости.

Процесс обнаружения точных разрывов яркости на изображении называется процессом выделение границ. Разрывы — это резкие изменения в группе пикселей, которые являются границами объектов. Классический алгоритм обнаружения границ задействует свертку изображения с помощью оператора, который основывается на чувствительности к большим перепадам яркости на изображении, а при проходе однородных участков возвращает нуль. Сейчас доступно огромное количество алгоритмов выделения контуров, но ни один из них не является универсальным. Каждый из существующих алгоритмов решает свой класс задач (т.е. качественно выделяет границы определенного типа). Для определения подходящего алгоритма выделения контуров необходимо учитывать такие параметры, как ориентация и структура контура, а также наличие и тип шума на изображении. Геометрия оператора устанавливает характерное направление, в котором он наиболее чувствителен к границам. Существующие операторы предназначены для поиска вертикальных, горизонтальных или диагональных границ. Выделение границ объектов — сложная задача в случае сильно зашумленного изображения, так как оператор чувствителен к перепадам яркости, и, следовательно, шум также будет считать некоторым объектом на изображении. Есть алгоритмы, позволяющие в значительной мере избавиться от шума, но в свою очередь, они в значительной мере повреждают границы изображения, искажая их. А так как большинство обрабатываемых изображений содержат в себе шум, шумоподавляющие алгоритмы пользуются большой популярностью, но это сказывается на качестве выделенных контуров.

Также при обнаружении контуров объектов существуют такие проблемы, как нахождение ложных контуров, расположение контуров, пропуск истинных контуров, помехи в виде шума, высокие затраты времени на вычисление и др. Следовательно, цель заключается в том, чтобы исследовать и сравнить множество обработанных изображений и проанализировать качество работы алгоритмов в различных условиях.

Алгоритмы выделения контуров изображений

В свете недавних статей об обработке изображений я хотел бы немного рассказать об алгоритмах выделения контуров: методы Робертса, Превитта и Собеля (эти методы взяты для рассмотрения как самые известные и часто используемые).
Не буду докучать объемной теорией, а ограничусь лишь минимальными сведениями, необходимыми для понимания сути алгоритмов.
Все указанные методы основываются на одном из базовых свойств сигнала яркости – разрывности. Наиболее общим способом поиска разрывов является обработка изображения с помощью скользящей маски, называемой также фильтром, ядром, окном или шаблоном, которая представляет собой некую квадратную матрицу, соответствующую указанной группе пикселей исходного изображения. Элементы матрицы принято называть коэффициентами. Оперирование такой матрицей в каких-либо локальных преобразованиях называется фильтрацией или пространственной фильтрацией.
Схема пространственной фильтрации иллюстрируется на рисунке ниже (см. рисунок 1).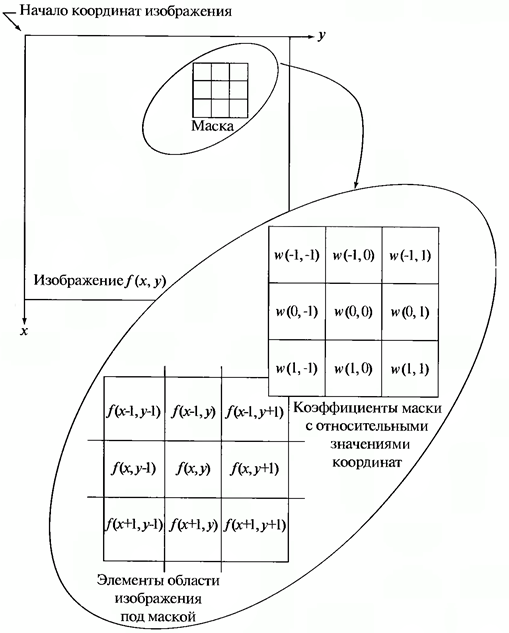


Рисунок 1. Схема пространственной фильтрации

Процесс основан на простом перемещении маски фильтра от точки к точке изображения; в

каждой точке (x,y) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отклик задается суммой произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Для маски 3х3 элемента, показанной на рисунке 1, результат (отклик) R линейной фильтрации в точке (x,y)изображения составит:

 (1.1)

что, как видно, есть сумма произведений коэффициентов маски на значения пикселей непосредственно под маской. В частности заметим, что коэффициент w(0,0) стоит при значении f(x,y), указывая тем самым, что маска центрирована в точке (x,y). 
При обнаружении перепадов яркости используются дискретные аналоги производных первого и второго порядка. Для простоты изложения будут рассмотрены одномерные производные. 
Первая производная одномерной функции f(x) определяется как разность значений соседних элементов: 

 (1.2)

Здесь использована запись в виде частной производной для того, чтобы сохранить те же обозначения в случае двух переменных f(x,y), где придется иметь дело с частными производными по двум пространственным осям. Использование частной производной не меняет существа рассмотрения.
Аналогично, вторая производная определяется как разность соседних значений первой производной:

 (1.3)

Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента. По определению, градиент изображения f(x,y) в точке (x,y) — это вектор [2]: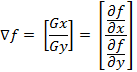

 (1.4)

Как известно из курса математического анализа, направление вектора градиента совпадает с направлением максимальной скорости изменения функции f в точке (x,y) [2].
Важную роль при обнаружении контуров играет модуль этого вектора, который обозначается ∇f и равен

 (1.5)

Эта величина равна значению максимальной скорости изменения функции f в точке (x,y), причем максимум достигается в направлении вектора ∇f. Величину ∇f также часто называют градиентом.
Направление вектора градиента также является важной характеристикой. Обозначим α(x,y) угол между направлением вектора ∇f в точке (x,y) и осью x. Как известно из математического анализа [2],

 (1.6)

Отсюда легко найти направление контура в точке (x,y), которое перпендикулярно направлению вектора градиента в этой точке. А вычислить градиент изображения можно, вычислив величины частных производных ∂f/∂x и ∂f/∂y для каждой точки.
Оператор Робертса

Пусть область 3х3, показанная на рисунке ниже (см. рис. 2), представляет собой значения яркости в окрестности некоторого элемента изображения.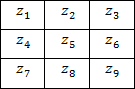


Рисунок 2. Окрестность 3х3 внутри изображения

Один из простейших способов нахождения первых частных производных в точке   состоит в применении следующего перекрестного градиентного оператора Робертса [1]:

 (1.7)
и
 (1.8)

Эти производные могут быть реализованы путем обработки всего изображения с помощью оператора, описываемого масками на рисунке 3, используя процедуру фильтрации, описанную ранее.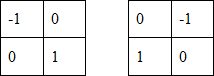


Рисунок 3. Маски оператора Робертса
Реализация масок размерами 2х2 не очень удобна, т.к. у них нет четко выраженного центрального элемента, что существенно отражается на результате выполнения фильтрации. Но этот «минус» порождает очень полезное свойство данного алгоритма – высокую скорость обработки изображения.

Оператор Превитта

Оператор Превитта, так же как и оператор Робертса, оперирует с областью изображения 3х3, представленной на рисунке 2, только использование такой маски задается другими выражениями:

 (1.9)
и
 (1.10)

В этих формулах разность между суммами по верхней и нижней строкам окрестности 3х3 является приближенным значением производной по оси x, а разность между суммами по первому и последнему столбцам этой окрестности – производной по оси y. Для реализации этих формул используется оператор, описываемый масками на рисунке 4, который называется оператором Превитта.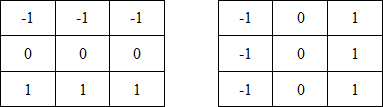


Рисунок 4. Маски оператора Превитта

Оператор Собеля

Оператор Собеля тоже использует область изображения 3х3, отображенную на рисунке 2. Он довольно похож на оператор Превитта, а видоизменение заключается в использовании весового коэффициента 2 для средних элементов:

 (1.11)
и
 (1.12)

Это увеличенное значение используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам. 

Маски, используемые оператором Собеля, отображены на рисунке ниже (см. рис. 5).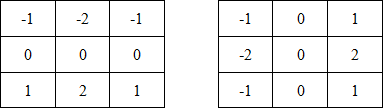



Рисунок 5. Маски оператора Собеля
Рассмотренные выше маски применяются для получения составляющих градиента  Для вычисления величины градиента эти составляющие необходимо использовать совместно:

 (1.14)
или
 (1.15)

Ну и в завершении продемонстрирую результаты обработки изображений (см. рисунки 6-8) описанными методами.


Рисунок 6. Исходное изображение №1


Рисунок 7. Исходное изображение №2


Рисунок 8. Исходное изображение №3

Результаты обработки методами Робертса, Превитта и Собеля продемонстрированы ниже: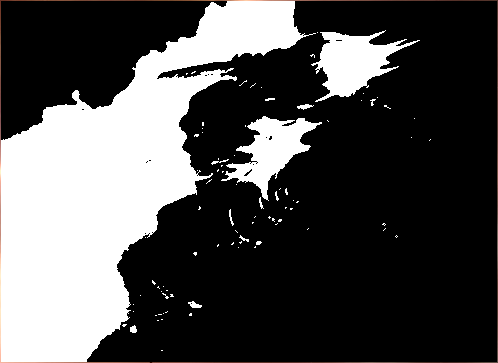



Рисунок 9. Исходные изображения после обработки методом Робертса




Рисунок 10. Исходные изображения после обработки методом Превитта




Рисунок 11. Исходные изображения после обработки методом Собеля

1.Алгоритмы обнаружения контуров изображения

При выделении контуров происходит замена полутонового изображения преобразованным, в котором исходные яркости заменены локальными контурными признаками (ЛКП). Если новое изображение, которое можно назвать контурным препаратом, далее используется для автоматической вторичной обработки (обнаружение или распознавание объектом, привязка изображений и др.), то к его характеристикам целесообразно предъявить определенные требования. Главное в них – это получение устойчивых результатов контурной   обработки. Качество сформированного контурного препарата по возможности не должно зависеть от таких характеристик исходного изображения, как средняя яркость, динамический диапазон яркостей, неравномерная освещенность сцены и т. п. Рассмотренный выше подход к решению задачи не способен автоматически обеспечивать эти качества, поскольку при изменении перечисленных характеристик изображения будут изменяться и результаты сравнения градиентного поля с порогом.

Весьма существенным является сочетание двух требовании. Первое заключается в том, чтобы среднее количество ложно обнаруженных ЛКП было стабилизировано при вариации перечисленных выше неконтролируемых характеристик исходных изображений. В этом случае вторичная обработка находится всегда в состоянии фиксированной вычислительной нагрузки. Это позволяет рационально проектировать вычислительное устройствобез неоправданных запасов его вычислительных ресурсов или при ограниченных ресурсах гарантирует выполнимость вычислений.

Второе требование состоит в необходимости обеспечить максимальную или близкую к ней вероятность правильного обнаружения истинных ЛКП.

Эти требования типичны для статистической проверки гипотез, применяемой при решении проблем обнаружения сигналов. В радиолокации получили мощное развитие методы обнаружения сигналов, которые сохраняют эффективность при априорно неизвестных характеристиках сигналов и помех. Вполне естественно, что эти методы начинают применяться и в задачах обработки изображений, поскольку условия их применения здесь достаточно близки к задачам радиолокационного обнаружения.

Один из методов, применяемых в условиях априорной неопределенности при обработке изображений, является ранговое обнаружение сигналов. В данном разделе будет рассмотрено его применение к обнаружению локальных контурных признаков.

Существенная черта рангового обнаружения (РО) – его способность обеспечивать постоянство вероятности ложного обнаружения при независимой помехе. При обнаружении ЛКП в роли помехи выступает фон изображения, который для обычных сцен является случайной двумерной функцией с сильно коррелированными (следовательно, и зависимыми) значениями. Потому непосредственное применение РО к исходному изображению не оправдано. Обнаружению в этих условиях должна предшествовать предобработка, делающая отсчеты фона независимыми.

Существуют два основных алгоритма трассировки квадратов и трассировка окрестностей Мура, просты в реализации, а потому часто применяются для определения контура заданного паттерна. К сожалению, у обоих алгоритмов есть несколько слабых мест, что приводит к невозможности обнаружения контура большого класса паттернов из-за их особого вида смежности.

Данные алгоритмы будут игнорировать все «дырки» в паттерне. Например, если у нас есть паттерн, подобный показанному на Рисунке 1, то обнаруженный алгоритмами контур будет похож на показанный на Рисунке 2 (синими пикселями обозначен контур). В некоторых областях применения это вполне допустимо, но в других областях, например, в распознавании символов, требуется обнаружение внутренних частей паттерна для нахождения всех пробелов, отличающих конкретный символ. (На Рисунке 3 показан «полный» контур паттерна.)



Следовательно, для получения полного контура сначала необходимо использовать алгоритм «поиска дырок», определяющий отверстия в заданном паттерне, а затем применить к каждому отверстию алгоритм обнаружения контуров.



Что такое связность

В цифровых изображениях с двоичными значениями пиксель может иметь одно из следующих значений: 1 — когда является частью паттерна, или 0 — когда является частью фона, т.е. градации серого отсутствуют. (Мы будем считать, что пиксели со значением 1 чёрные, а со значением 0 — белые).

Для идентификации объектов в цифровом паттерне нам нужно находить группы чёрных пикселей, «связанных» друг с другом. Другими словами, объектами в заданном цифровом паттерне являются связные компоненты этого паттерна.

В общем случае, связная компонента — это множество чёрных пикселей P, такое, что для каждой пары пикселей pi и pj в P существует последовательность пикселей pi, ..., pj, такая, что:

a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и

b) каждые 2 пикселя, находящиеся в последовательности рядом, являются «соседями».

Возникает важный вопрос: когда мы можем сказать, что 2 пикселя являются «соседями»? Поскольку мы используем квадратные пиксели, ответ на предыдущий вопрос нетривиален по следующей причине: в квадратной тесселяции пиксели имеют общее или ребро, или вершину, или не имеют ничего общего. У каждого пикселя есть 8 пикселей, имеющих с ним общую вершину; такие пиксели составляют «окрестность Мура» данного пикселя. Должны ли мы считать «соседями» пиксели, имеющие только одну общую вершину? Или чтобы считаться «соседями», два пикселя должны иметь общее ребро?

Так возникают два вида связности, а именно: 4-связность и 8-связность.

4-связность

Когда мы можем сказать, что заданное множество чёрных пикселей является 4-связным? Во-первых, нужно определить понятие 4-соседа (также называемого прямым соседом):

Определение 4-соседа: пиксель Q является 4-соседом заданного пикселя P, если Q и P имеют общее ребро. 4-соседи пикселя P (обозначенные как P2, P4, P6 и P8), показаны на Рисунке 2 ниже.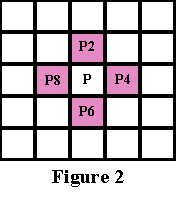




Определение 4-связной компоненты: множество чёрных пикселей P является 4-связной компонентой, если для каждой пары пикселей pi и pj в P существует последовательность пикселей pi, ..., pj, такая, что:

a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и

b) каждые два пикселя, которые находятся рядом в последовательности, являются 4-соседями

Примеры 4-связных паттернов

На Рис. 4 ниже показаны примеры 4-связных паттернов: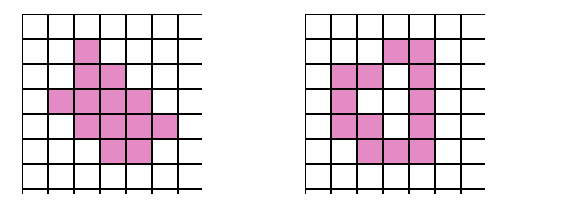



8-связность

Когда можно сказать, что заданное множество чёрных пикселей 8-связное? Во-первых, нам нужно определить понятие 8-соседа (также называемого непрямым соседом):

Определение 8-соседа: пиксель Q является 8-соседом (или просто соседом) заданного пикселя P, если Q и P имеют общее ребро или вершину. 8-соседи заданного пикселя P составляют окрестность Мура этого пикселя.

Определение 8-связной компоненты: множество чёрных пикселей P является 8-связной компонентой (или просто связной компонентой), если для каждой пары пикселей pi и pj в P существует последовательность пикселей pi, ..., pj, такая, что:

a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и

b) каждые два пикселя, которые находятся рядом в этой последовательности, являются 8-соседями

Примечание: все 4-связные паттерны являются 8-связными, т.е. 4-связные паттерны являются подмножеством множества 8-связных паттернов. С другой стороны, 8-связный паттерн может и не являться 4-связным.

Пример 8-связного паттерна

На Рис.5 показан паттерн, являющийся 8-связным, но не 4-связным: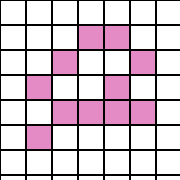



Пример паттерна, не являющегося 8-связным:

На Рис.6 ниже показан пример паттерна, не являющийся 8-связным, т.е. составленный из более чем одной связной компоненты (на схеме показаны три связные компоненты):



1.1Алгоритм трассировки квадратов

Идея лежащая в основе алгоритма трассировки квадратов идея очень проста; это можно связать с тем фактом, что алгоритм стал одной из первых попыток обнаружения контура двоичного паттерна.

Чтобы понять, как он работает, нужно немного воображения…

Допустим, у нас есть цифровой паттерн, например, группа из чёрных пикселей на фоне из белых пикселей, т.е. на сетке; находим чёрный пиксель и объявляем его нашим "начальным" пикселем. (Нахождение "начального" пикселя можно реализовать множеством разных способов; мы начнём с левого нижнего угла сетки, будем сканировать каждый столбец пикселей снизу вверх, от самого левого столбца и до самого правого, пока не натолкнёмся на чёрный пиксель. Его мы и объявим "начальным".)

Теперь представьте, что вы — божья коровка, стоящая на начальном пикселе, как это показано на показанном ниже Рисунке 1. Чтобы получить контур паттерна, вам необходимо сделать следующее:

каждый раз, когда вы оказываетесь на чёрном пикселе, поворачивайте налево, и

каждый раз, когда вы оказываетесь на белом пикселе, поворачивайте вправо,

пока снова не доберётесь до начального пикселя.

Чёрные пиксели, которые вы обошли, будут являться контуром паттерна.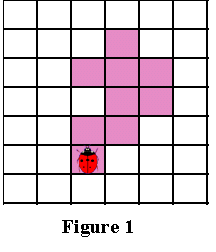



Важным аспектом алгоритма трассировки квадратов является «чувство направления». Повороты влево и вправо выполняются относительно текущего расположения, которое зависит от того, каким образом вы попали на текущий пиксель. Следовательно, чтобы делать правильные ходы, необходимо отслеживать своё направление.

1.2. Алгоритм,анализ и критерий останова

Алгоритм

Ниже представлено формальное описание алгоритма трассировки квадратов:

Входящие данные: квадратная тесселяция, T, содержащая связную компоненту P чёрных ячеек.

Выходные данные: ряд B (b1, b2 ,..., bk) пикселей границы, т.е. контур.

Начало

Задаём B как пустое множество.

Сканируем снизу вверх и слева вправо ячейки T, пока не будет найден чёрный пиксель s из P.

Вставляем s в B.

Делаем текущий пиксель p начальным пикселем s.

Поворачиваем влево, т.е. переходим в соседний пиксель слева от p.

Обновляем p, т.е. он становится текущим пикселем.

Пока p не равно s, выполняем

Если текущий пиксель p является чёрным

вставляем p в B и поворачиваем влево (переходим в соседний пиксель слева от p).

Обновляем p, т.е. он становится текущим пикселем.

иначе

поворачиваем вправо (переходим в соседний пиксель справа от p).

Обновляем p, т.е. он становится текущим пикселем.

Завершение цикла «Пока»

Анализ

Оказывается, что возможности алгоритма трассировки квадратов очень ограничены. Он неспособен обнаруживать контуры большого семейства паттернов, которые часто возникают в реальных областях применения.

В основном это связано с тем, что повороты влево и вправо не учитывают пиксели, расположенные «по диагонали» от текущего пикселя.

Давайте рассмотрим различные паттерны с разной связностью и увидим, почему терпит неудачу алгоритм трассировки квадратов. Кроме того, мы изучим способы усовершенствования возможностей алгоритма и заставим его работать хотя бы с паттернами, имеющими особый вид связности.

Критерий останова

Одна из слабостей алгоритма заключается в выборе критерия останова. Другими словами, когда алгоритм прекращает своё выполнение?

В исходном описании алгоритма трассировки квадратов условием завершения является попадание в начальный пиксель во второй раз. Оказывается, что если алгоритм зависит от такого критерия, то он не сможет обнаружить контуры большого семейства паттернов.

Как видите, усовершенствование критерия останова может стать хорошим началом для улучшения результативности алгоритма в целом. Существует две эффективные альтернативы для имеющегося критерия останова:

a) Останавливаться, только посетив начальный пиксель n раз, где n не меньше 2, ИЛИ

b) Останавливаться после попадания в начальный пиксель во второй раз точно так же, как мы попали в него изначально.

Этот критерий был предложен Джейкобом Элиософфом, поэтому мы будем называть его критерием останова Джейкоба.

Смена критерия останова в общем случае улучшает результативность алгоритма трассировки квадратов, но не позволяет преодолеть другие слабые места, которые он имеет в случае паттернов с особыми видами связности.

Square Tracing Algorithm неспособен обнаружить контур семейства паттернов со связностью 8, которые НЕ имеют связности 4.

Если прочитать представленный выше анализ, то можно сделать вывод, что алгоритму трассировки квадратов не удаётся обнаружить контуры большинства паттернов. Но оказывается, что существует особое семейство паттернов, у которого полностью правильно обнаруживается контур алгоритмом трассировки квадратов.

Пусть P — множество чёрных пикселей со связностью 4 на сетке. Пусть белые пиксели сетки, т.е. фоновые пиксели W тоже имеют связность 4. Оказывается, что при таких условиях паттерна и его фона можно доказать, что алгоритм трассировки квадратов (с критерием останова Джейкоба) всегда успешно будет справляться с определением контура.

Ниже представлено доказательство, что в случае, когда и паттерн, и пиксели фона имеют связанность 4, алгоритм трассировки квадратов будет правильно определять контур при использовании критерия останова Джейкоба.

Доказательство
Дано: паттерн P такой, что все пиксели паттерна (т.е. чёрные) и пиксели фона (т.е. белые) W имеют связность 4.

1.3. Наблюдения.

Первое наблюдение

Так как множество белых пикселей W имеет связность 4, это значит, что в паттерне не может быть никаких "дыр" (выражаясь неформально, "дырами" мы называем группы белых пикселей, полностью окружённые чёрными пикселями паттерна).

Наличие любой "дыры" в паттерне приведёт к отделению группы белых пикселей от остальных белых пикселей; при этом множество белых пикселей теряет связность 4.

На  Рисунке 7 ниже показано два вида "дыр", которые могут возникнуть в паттерне со связностью 4: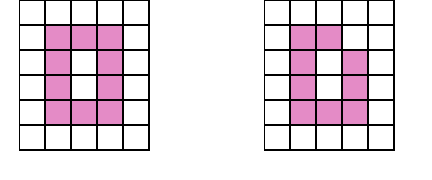



Рис.7 Виды «дыр», возникаемые в паттене с 4-связностью.

Второе наблюдение

Любые два чёрных пикселя паттерна ОБЯЗАНЫ иметь одну общую сторону.

Допустим, два чёрных пикселя имеют только одну общую вершину. Тогда, чтобы удовлетворить свойству 4-связности паттерна, должен существовать путь, соединяющий эти два пикселя так, что каждые два соседних пикселя на этом пути имеют связность 4. Но это даст нам паттерн, похожий на Рисунок 7. Другими словами, это приведёт к разделению белых пикселей. На Рисунке 8 ниже показан типичный паттерн, удовлетворяющий допущению, что пиксели паттерна и фона 4-связаны, т.е. не имеют "дыр", а каждые два чёрных пикселя имеют одну общую сторону:



Рис. 8 Типичный паттерн с 4-связностью, не имеющий «дыр».

Полезно представлять такие паттерны следующим образом:

Сначала рассматриваем граничные пиксели, т.е. контур паттерна. Затем если мы рассмотрим каждый граничный пиксель как имеющий 4 ребра единичной длины, то увидим, что некоторые из этих рёбер общие с соседними белыми пикселями. Мы назовём такие рёбра граничными рёбрами.

Такие граничные рёбра можно рассматривать как рёбра многоугольника. На Рисунке
9 ниже эта мысль продемонстрирована на примере многоугольника, соответствующего паттерну с Рисунка 8 выше:



Рис. 9 Многоугольник, соответствующий паттерну, с граничными ребрами.

Если мы рассмотрим все возможные «конфигурации» граничных пикселей, которые могут возникать в таких паттернах, то увидим, что существует два простых случая, показанных на Рисунке 10 ниже.

Граничные пиксели могут быть кратными этих случаев или другими расположениями, т.е. поворотами этих двух случаев. Граничные рёбра помечены синим как E1, E2, E3 и E4.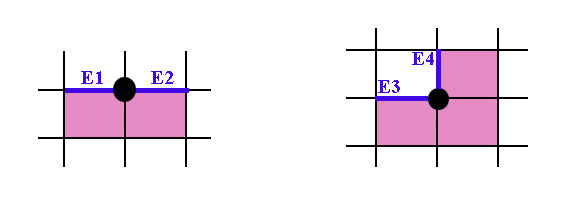



Рис. 10 Примеры сторон с граничными пикселями.

Третье наблюдение

В случае рассмотренных выше двух случаев, какой бы начальный пиксель мы не выбрали, и в каком бы направлении в него не попали, алгоритм трассировки квадратов никогда не будет «возвращаться назад» (backtrack), никогда не будет «проходить через» граничное ребро дважды (только если он не трассирует границу во второй раз) и никогда не пропустит граничное ребро. Проверьте!

Здесь нужно пояснить две концепции:

a) алгоритм «возвращается назад», когда перед трассировкой всей границы он идёт назад, чтобы посетить уже посещённый пиксель, и

b) для каждого граничного ребра существует два способа «пройти через него», а именно «внутрь» и «наружу» (где «внутрь» обозначает движение внутрь соответствующего многоугольника, а «наружу» — наружу многоугольника).

Кроме того, когда алгоритм проходит «внутрь» через одно из граничных рёбер, он пройдёт «наружу» через следующее граничное ребро, т.е. алгоритм трассировки квадратов не должен иметь возможности пройти сквозь два последовательных ребра одинаковым образом.

Последнее наблюдение

У каждого паттерна существует чётное количество граничных рёбер.

Если посмотреть на многоугольник с Рисунка 10, то можно увидеть, что:

если мы хотим начать с вершины S, отмеченной на схеме, и следовать по граничным рёбрам, пока снова не достигнем S, то заметим, что пересечём в процессе чётное количество граничных рёбер. Можно считать каждое граничное ребро «шагом» в отдельном направлении. Тогда для каждого «шага» вправо должен быть соответствующий «шаг» влево, если мы хотим вернуться в исходную позицию. То же самое относится к вертикальным «шагам». Следовательно, «шаги» должны иметь соответствующие пары и это объясняет, почему в каждом из таких паттернов будет чётное количество граничных рёбер.

Следовательно, когда алгоритм трассировки квадратов входит через начальное граничное ребро(начального пикселя) во второй раз, то он будет это делать в том же направлении, что и в первый раз.

Причина этого в том, что поскольку существует два способа прохода через граничное ребро, и алгоритм попеременно выполняет движение «внутрь» и «наружу», а граничных рёбер чётное количество, то алгоритм пройдёт через начальное граничное ребро во второй раз так же, как и в первый.

Заключение

В случае 4-связного паттерна и фона алгоритм трассировки квадратов обнаружит всю границу, т.е. контур, паттерна и прекратит работу после однократной трассировки, т.е. не будет трассировать её заново, поскольку при достижении начального граничного ребра во второй раз он войдёт в него так же, как и в первый раз. Следовательно, алгоритм трассировки квадратов с критерием останова Джейкоба будет правильно определять контру любого паттерна при условии, что и паттерн, и фон обладают 4-связностью.

Трассировка окрестностей Мура

Идея

Идея, лежащая в основе трассировки окрестностей Мура (Moore-Neighbor tracing), проста; но, прежде чем объяснять её, нам нужно объяснить важное понятие: окрестности Мура пикселя.

Окрестность Мура

Окрестность Мура пикселя P — это множество из 8 пикселей, имеющих общую вершину или ребро с этим пикселем. Такие пиксели, а именно P1, P2, P3, P4, P5, P6, P7 и P8, показаны на Рисунке 1.

Окрестность Мура (Moore neighborhood, также называемая 8-соседями или indirect neighbors (непрямыми соседями)) — это важное понятие, часто упоминаемое в литературе.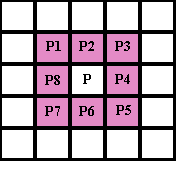



Рис. 11 Пример окрестности Мура пикселя Р.

Теперь мы готовы познакомиться с идеей, лежащей в основе трассировки окрестностей Мура.

Пусть существует цифровой паттерн, т.е. группа чёрных пикселей, на фоне из белых пикселей, т.е. на сетке; найдём чёрный пиксель и объявим его "начальным" пикселем. (Находить "начальный" пиксель можно разными способами, но мы, как и раньше, будем начинать с левого нижнего угла и сканировать все столбцы пикселей по порядку, пока не найдём первый чёрный пиксель, который и объявим "начальным".)

Божья коровка, стоящая на начальном пикселе будет пытаться обнаруживать контур, двигаясь вокруг паттерна по часовой стрелке. (Неважно, какое направление мы выберем, главное — использовать его в алгоритме постоянно).

Общая идея заключается в следующем: каждый раз, когда мы попадаем в чёрный пиксель P, то возвращаемся назад, то есть к белому пикселю, в котором стояли ранее. Затем обходим пиксель P по часовой стрелке, посещая каждый пиксель в его окрестности Мура, пока не попадём в чёрный пиксель. Алгоритм завершает выполнение, когда начальный пиксель достигает начального пикселя во второй раз.

Те чёрные пиксели, которые посетил алгоритм, будут контуром паттерна.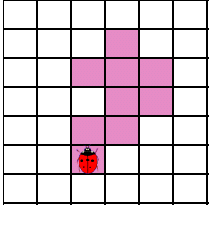



Рис 12. Пример алгоритма окрестности мура.

2.1. Алгоритм,анализ и критерий останова

Алгоритм

Ниже приведено формальное описание алгоритма трассировки окрестностей Мура:

Входящие данные: квадратная тесселяция T, содержащая связную компоненту P из чёрных ячеек.

Выходные данные: ряд B (b₁, b₂ ,..., b_k) граничных пикселей, т.е. контур.

Обозначим как M(a) окрестность Мура пикселя a.

Пусть p будет текущим граничным пикселем.

Пусть c будет текущим рассматриваемым пикселем, т.е. c находится в M(p).

Начало

• 
  Задаём B как пустое множество.
  
• 
  Снизу вверх и слева направо сканируем ячейки T, пока не найдём чёрный пиксель s из P.
  
• 
  Вставим s в B.
  
• 
  Зададим в качестве текущей граничной точки p точку s, т.е. p=s
  
• 
  Вернёмся назад, т.е. перейдём к пикселю, из которого мы пришли в s.
  
• 
  Зададим в качестве c следующий по часовой стрелке пиксель в M(p).
  
• 
  Пока c не равно s, выполняем
  
  • 
    если c — чёрный
    
    • 
      Вставляем c в B
      
    • 
      задаём p=c
      
    • 
      возвращаемся назад (перемещаем текущий пиксель c в пиксель, из которого попали в p)
      

иначе

• 
  перемещаем текущий пиксель c в следующий по часовой стрелке пиксель в M(p)
  

Конец цикла «Пока»


Конец

Анализ

Основная слабость трассировки окрестностей Мура заключается в выборе критерия останова.

В исходном описании алгоритма для трассировки окрестностей Мура критерием останова является попадание в начальный пиксель во второй раз. Аналогично алгоритму трассировки квадратов, оказывается, что трассировка окрестностей Мура при использовании такого критерия не может обнаруживать контуры большого семейства паттернов.

Как видите, усовершенствование критерия останова может стать хорошим началом для улучшения результативности трассировки в целом. Для критерия останова есть две эффективные альтернативы, аналогичные критерию останова Джейкоба.

Использование критерия Джейкоба значительно улучшает результативность трассировки окрестностей Мура, делая его наилучшим алгоритмом для определения контура любого паттерна, вне зависимости от его связности.

Причина этого в основном заключается в том, что для поиска следующего граничного пикселя алгоритм проверяет всю окрестность Мура граничного пикселя. В отличие от алгоритма трассировки квадратов, который делает повороты только влево и вправо и упускает пиксели «по диагонали», трассировка окрестностей Мура всегда будет способна обнаружить внешнюю границу любой связной компоненты. Причина заключается в следующем: для любого 8-связного (или просто связного) паттерна следующий граничный пиксель лежит в пределах окрестности Мура текущего граничного пикселя. Поскольку трассировка окрестностей Мура проверяет каждый из пикселей в окрестности Мура текущего граничного пикселя, она обязана обнаружить следующий граничный пиксель.

Когда трассировка окрестностей Мура достигает начального пикселя во второй раз точно так же, как она сделала это в первый раз, то это значит, что был обнаружен полный внешний контур паттерна, и если не остановить алгоритм, то он заново будет обнаруживать тот же контур.

3.Применения ранговых алгоритмов

Кроме применений для сглаживания, усиления детальности, выделения деталей изображений и границ деталей, ранговые алгоритмы могут употребляться также для решения многих других более частных задач обработки изображений. Из них можно упомянуть диагностику искажений видеосигнала и определение их статистических характеристик, стандартизацию изображений, определение статистических характеристик самого видеосигнала и измерение текстурных признаков.

Автоматическая диагностика параметров помех и искажений видеосигнала. Она может основываться на принципе обнаружения и измерения аномалий в статистических характеристиках видеосигнала. Для обнаружения аномалий можно использовать ранговые алгоритмы, такие как алгоритм голосования проверки принадлежности анализируемого элемента выборки к заданному числу крайних (наибольших или наименьших) значений упорядоченной выборки.

Стандартизация изображений. Стандартизация - это приведение характеристик изображений к некоторым заданным. С помощью ранговых алгоритмов может быть достаточно просто осуществлена стандартизация гистограмм, т. е. преобразование видеосигнала, делающее гистограмму распределения его значений заданной. В зависимости от задачи могут использоваться глобальная и локальная стандартизация гистограмм. В качестве *стандартной может использоваться не вся гистограмма стандартного изображения или его локальные гистограммы, а соответствующие гистограммы по локальным окрестностям.

Определение статистических характеристик видеосигнала и измерение текстурных признаков. Адаптивные свойства ранговых алгоритмов делают их удобным инструментом для измерения локальных статистических характеристик изображений: локального среднего, локальной дисперсии и других моментов распределения. Очевидно, что эти и другие подобные характеристики гистограмм являются также текстурными характеристиками изображений.

Ранговые алгоритмы могут служить для оценки не только гистограммных текстурных признаков, но и для оценки текстурных признаков, связанных с локальными пространственными статистическими характеристиками изображений. Одним из простейших признаков такого рода является число локальных экстремумов S-окрестности обрабатываемого элемента. Ряд текстурных признаков связан с характеристиками пространственного распределения локальных экстремумов, т.е. среднего расстояния между ними, дисперсии расстояний между ними и т.д. Более общими являются признаки, характеризующие пространственное распределение рангов в обрабатываемом фрагменте. В частности, текстурным признаком является число перемен знака первой производной по фрагменту эквализованного изображения в заданном направлении сканирования. Ряд текстурных признаков можно рассматривать как параметры пространственного распределения элементов, принадлежащих локальным окрестностям, в частности, моменты распределения взаимных расстояний между ними.

Кодирование изображений. Возможность применения ранговых алгоритмов для кодирования изображений связана с использованием алгоритмов адаптивного квантования мод в режиме пофрагментной обработки. В этом случае анализируется гистограмма распределения значений элементов изображения в пределах фрагмента (или, как принято говорить в кодировании, блока), находятся границы кластеров, которые выбираются в качестве границ интервалов квантования, и производится квантование всех отсчетов фрагмента в соответствии с найденными границами.

Заключение

Обработка изображений - быстро развивающаяся область в дисциплине компьютерного зрения. Ее рост основывается на высоких достижениях в цифровой обработке изображений, развитию компьютерных процессоров и устройств хранения информации. 

Просмотрев результаты работы двух алгоритмов на практике, можно заключить, что самым качественным методом оказался метод трассировка окрестностей Мура. Поскольку именно этот метод позволит ярко выделить границы, понизить интенсивность фона изображения и качественно обозначить все элементы изображения.

В данном курсовом проекте была предпринята попытка изучить алгоритмы для рангового обнаружения контуров. Даже учитывая тот факт, что вопрос обнаружения границ на изображении достаточно хорошо осветлен в современной технической литературе, он все же до сих пор остается достаточно трудоемкой задачей, так как качественное выделение границ всегда зависит от множества влияющих на результат факторов.

Список литературы.

1.Р. Гонсалес, Р. Вудс Цифровая обработка изображений — М: Техносфера, 2005 – 1007с

2.Кудрявцев Л.В. Краткий курс математического анализа – M.: Наука, 1989 – 736с

3.Анисимов Б.В. Распознавание и цифровая обработка изображений – М.: Высш. школа, 1983 – 295с

4.Карпов, Ю. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5 {Текст}/Ю Карпов.-СПб.: БВХ-Петербург,2005.-400 с.