100 баллдық вышмат. Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген

• Название: Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген
• Дата: 14.05.2022
• Размер: 2.07 Mb.
• Имя файла: 100 баллдық вышмат.docx
• Тип: Документы; #528273
• страница: 6 из 6

Егер әрбір тәжірибеде А оқиғасының пайда болу р ықтималдығы тұрақты және нөл мен бірден өзгеше болса, онда ықтималдығы n тәжірибе жүргізгенде А оқиғасы k рет пайда болады, (n үлкен болған сайын нақты) жуық түрде функцияның мәні
#53

*!Бернулли формуласының орнына Лаплас формуласын қолданудың артықшылығы

: егер n тым улкен болса, р аз болганда накты жауапка жакын Лаплас формуласымен аныктай аламыз
#54

*! Лапластың интегралдық теремасын қолдану ...негізделген:

+оқиғаның n сынауда k1-ден k2-ге дейiн пайда болуын. Немесе Егер әрбір тәжірибеде А оқиғасының пайда болу р ықтималдығы тұрақты және нөл мен бірден өзгеше болса, онда ықтималдығы n тәжірибе жүргізгенде А оқиғасы k1 - ден k2-ге дейін пайда болады, жуық түрде анықталған интегралға тең:


#55

*!Пуассонның таралу заңы деп таралу деп аталады, оның ықтималдығы формуламен анықталатын таралуды айтамыз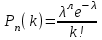

_{Бұл формула (n үлкен) және (р аз) сирек оқиғалар үшін Пуассонның таралу заңы деп аталады}

#56

*!Таралудың қалыпты заңы деп - ықтималдылық тығыздығымн анықталатын таралуды айтамыз.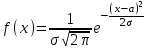


#1

*!Х кездейсоқ шамасы (0,1) аралығында f(х)=2х+1 тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 7/6

#2

Орта квадраттық ауытқуды есептеу формуласы:

#3

*! Х үзiлiссiз кездейсоқ шаманың қабылдайтын мүмкін мәндері Ох осінің бойында жатса, математикалық күтімнің формуласы: +M(x)=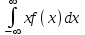

3.

#4

*! Х кездейсоқ шамасы (0,1) аралығында f(х)=3х² тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 3/4

#5

*! М(С)=С нені білдіреді:

Тұрақты шаманың математикалық күтімі өзіне тең, яғни С тұрақты болса: М(С)=C.

#6

*!М(СХ)=СМ(Х) нені білдіреді: Тұрақты шаманы математикалық күтімнің алдына шығаруға болады:

#7

*! М(ХУ)=М(Х)М(У) нені білдіреді: Екі тәуелсіз кездейсоқ шама көбейтіндісінің математикалық күтімі олардың математикалық күтімдерінің көбейтіндісіне тең

#8

*! М(Х+У)=М(Х)+М(У) нені білдіреді: Екі тәуелсіз кездейсоқ шаманың қосындысының математикалық күтімі, қосылғаштардың математикалық күтімдерінің қосындысына тең

#9*! М(Х+У+Z)=М(Х)+М(У)+M(Z) нені білдіреді: + Бірнеше кездейсоқ шамалардың қосындысын математикалық өңдеу олардың математикалық өңдеу жиынтығына тең.

#10.Үздiксiз кездейсоқ шаманың ықтималдықтарының таралу тығыздығы: *+F(x) таралу функциясының бiрiншi реттi туындысы - f(x) функциясы.

#11

*!Үздiксiз кездейсоқ шаманың берiлген аралыққа түсу ықтималдығын есептеу формуласы: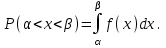

# 12

*!Үздiксiз кездейсоқ шаманың [a;b] аралығында жатқан мәндердi қабылдау ықтималдығы: +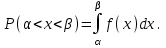

#13.

*! X кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген: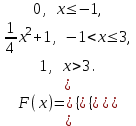

X –тің мәні (0; 2) интервалына тиісті болатыныy ықтималдықты табыңыз: 1

#14

*! Х кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген,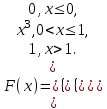



X –тің мәні (0,1) интервалына тиісті болатын ықтималдылықты табыңыз: 1

#15

*! Х кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген: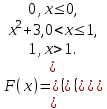



М(Х) –ті табыңыз: 2/3

#16

*!Х кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген



D(X)-ті табыңыз: 1/12

#17

*! Х кездейсоқ шамасы (0,1) аралығында f(х)=5х тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 5/3

#18

*! Х кездейсоқ шамасы (0,2) аралығында f(х)=3х тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 8

#19

*! Х кездейсоқ шамасы (0,2) аралығында f(х)=2х² тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 8

#20

*! Х кездейсоқ шамасы (0,1) аралығында f(х)=х тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 1/3

#21

*!Х кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген



D(X)-ті табыңыз: 5/48

#22

*!Х кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген



D(X)-ті табыңыз: 1/12

#23.

*! X кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген:

X –тің мәні (0; 2) интервалына тиісті болатыныy ықтималдықты табыңыз: 2

#24

*! Х кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген,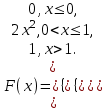



X –тің мәні (0; 1) интервалына тиісті болатыныy ықтималдықты табыңыз: 2

#25

*! Мүмкін мәндері [а,в] кесіндісінде жататын Х үздіксіз кездейсоқ шаманың дисперсиясы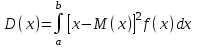



#26

*! Мүмкін мәндері [а,в] кесіндісінде жататын Х үздіксіз кездейсоқ шамасының математикалық күтімі деп: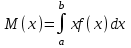



#27.

*! X кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген: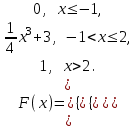

X –тің мәні (0; 1) интервалына тиісті болатыныy ықтималдықты табыңыз: 1/4 или 13/4

#28.

*! X кездейсоқ шамасының үлестіру заңы интегралдық функциясымен берілген: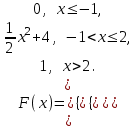

X –тің мәні (0; 1) интервалына тиісті болатыныy ықтималдықты табыңыз: 9/2 или 1/2